Des problèmes inspirés du livre
Les mathématiques et le réel

Dans cet article déjà publié dans la revue Losanges n° 45 en 2019, Thérèse Gilbert s’intéresse à quelques problèmes, tous inspirés du livre collectif Les mathématiques et le réel, qui vous permettront d’enrichir vos cours de maths de problématiques en lien avec l’histoire des maths et le réel.

Thérèse Gilbert

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Introduction

Les mathématiques et le réel [1] est un ouvrage collectif écrit sous la direction d’Évelyne Barbin, Dominique Bénard et Guillaume Moussard. Il présente des exemples d’introduction d’une perspective historique dans l’enseignement, sur des thèmes qui touchent au réel.

La première partie s’intéresse aux instruments pour mesurer des grandeurs et pour tracer des figures : les balances et l’équilibre chez Archimède, Stevin ou Camus, la dioptre d’Héron d’Alexandrie, le graphomètre, des mesureurs d’angles, des compas, des pantographes, des traceurs…

La deuxième partie présente des instruments pour calculer : des machines pour multiplier, les machines arithmétiques de Blaise Pascal, des échiquiers pour calculer, des tables métrologiques…

La troisième partie se situe au cœur des conflits entre « le réel, toujours inaccessible, et une réalité, construite avec les mathématiques » [1] : modèles cosmologiques chinois et grecs, leviers et balances, étude des mines, cancer et hasard…

Voici quelques problèmes qui illustrent le type de problématiques exposées. Nous donnons quelques éléments de réponses, sans tout dévoiler des solutions.

Balances et équilibre

L’équipe GRHEM¹ analyse les relations entre l’expérience et les mathématiques dans le contexte des balances et de l’équilibre. Elle étudie notamment le principe de la balance chez Simon Stevin (De la statique ou l’art pondéraire, 1634 [2]) et Charles Étienne Louis Camus (Cours de mathématiques, 1752 [3]). Voici deux des problèmes traités (reformulés ici).

Problème 1. Balance et proportionnalité

On considère une balance suspendue en équilibre comme à la figure 1.

Figure 1 : La balance chez STEVIN.

Si on donne la mesure \(\mathsf{P}\) de l’une des masses, est-il possible de déterminer l’autre en tenant compte des distances visibles sur la figure 1 ?

La figure 2 suggère de s’intéresser au rapport de certaines longueurs. L’équipe GHREM propose de soumettre ce type de problème dans une approche de la proportionnalité, en utilisant de vraies balances pour que l’expérimentation vienne renforcer la compréhension du phénomène.

Figure 2. Balance et proportionnalité.

La solution au problème suivant de poids suspendus est nettement moins évidente.

Problème 2. Poids suspendus et triangles semblables

Deux masses sont attachées à une ficelle dont les deux extrémités sont fixées, comme à la figure 3.

Figure 3. La balance de CAMUS.

Si on donne la mesure \(\mathsf{P}\) de l’une des masses, est-il possible de déterminer l’autre en tenant compte des positions des différentes parties de ficelle ?

Voilà une situation qui donne envie d’expérimenter, à peu de frais. Une ficelle, des masses quelconques et on essaie de comprendre comment cela peut fonctionner. On simplifie la situation pour mieux y revenir ensuite.

Dans Les mathématiques et le réel, ce problème est heureusement précédé d’une autre situation un peu plus élémentaire ou une seule masse est suspendue (figure 4). On y retrouve le « parallélogramme des forces » qui nous donne la façon dont les forces se répartissent sur \(\mathsf{AQ}\) et \(\mathsf{AP}\).

Figure 4. Le poids suspendu chez CAMUS.

La figure 5a suggère une solution du problème 2. On y voit les parallélogrammes des forces dont les résultantes sont représentées par des segments verticaux, \(\mathsf{CH}\) et \(\mathsf{BF}\), dont les longueurs sont entre elles comme les masses suspendues. Ces segments sont des côtés des deux triangles semblables \(\mathsf{KFB}\) et \(\mathsf{KCH}\), que l’on retrouve, placés différemment, à la figure 5b : ils ont subi une symétrie centrale. Finalement, en prolongeant deux morceaux de ficelle, en traçant deux verticales, on détermine donc des segments dont les longueurs sont inversement proportionnelles aux masses.

(a)

(b)

Figure 5. La balance de CAMUS, éléments de solution.

Mesures d’angles

Jean-Paul Mercier présente quelques instruments de mesure d’angles du xvi^e au xxi^e siècle comme objets d’étude en classe. L’idée est « d’étudier la conception d’outils élaborés par des hommes (…) pour mettre en action des propriétés mathématiques ».

Pour reporter des angles, avec les élèves de 12 ans, J.-P. Mercier propose d’utiliser la fausse équerre (figure 6), avant d’employer le rapporteur. La fausse équerre est un appareil articulé, constitué seulement de deux tiges rectilignes assemblées en une de leurs extrémités.

Cet instrument permet de reporter exactement les angles mais non de mesurer leur amplitude. Le rapporteur, lui, permet de mesurer des amplitudes mais n’est pas un outil très pratique pour reporter des angles, surtout s’il faut construire des angles de même amplitude en grand nombre.

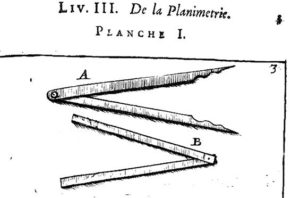Figure 6. La fausse équerre ([4] planche I, p. 3).

La question suivante est alors posée aux élèves.

Problème 3. Récipiangle et propriétés des angles

Quel outil permettrait à la fois de reporter facilement des angles, comme la fausse équerre, et de mesurer des amplitudes, comme le rapporteur ?

Certains élèves proposent d’en inventer un et le fruit de leurs cogitations correspond en fait au récipiangle (figure 7) de Manesson-Mallet [4] ou de Bion [5].

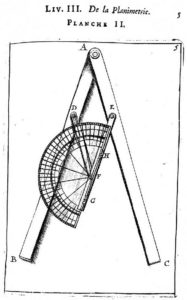Figure 7. Le récipiangle ([4] planche II, p. 5).

Les élèves justifient leur conception. On leur présente le texte de Bion où il évoque, pour justifier sa construction, les propriétés du losange (parallélogramme équilatéral). On approfondit les propriétés liées à la conception de ces outils, dont les égalités d’amplitudes d’angles liées au parallélisme.

D’autres instruments sont présentés, tel le porte-crayon de Manesson-Mallet, qui permet de mesurer un angle à l’aide d’une ficelle graduée et d’une table de cordes. Certains sont faciles à construire et peuvent être expérimentés sur le terrain, avec des élèves.

Des machines mathématiques pour la classe

Problème 4. Machines à tracer et transformations du plan

Quelle sera la figure tracée à l’aide du crayon par la machine représentée en magenta si la pointe sèche suit le contour du pentagone ?

Figure 8. Machine 1.

Michela Maschietto s’intéresse à des machines mathématiques que l’on rencontre dans l’histoire et à la façon dont elles peuvent être utilisées dans l’enseignement. Elles sont construites pour la classe dans un but didactique.

La propriété des diagonales du losange est mise en relation avec la définition de symétrie orthogonale.

Et dans le cas de la figure 9, où \(\mathsf{Q}\) et \(\mathsf{R}\) sont fixés sur les tiges \(\mathsf{PA}\) et \(\mathsf{PB}\) mais coulissent dans la fente ?

Figure 9. Machine 2 : le projecteur de DELAUNAY.

La machine 2 de la figure 9 est décrite dans un traité de Delaunay [6].

L’étude de ces machines par les élèves passe par différentes phases : manipulation, description (qu’est-ce qui change, qu’est-ce qui ne change pas lors de l’utilisation de la machine ?), conjectures et justification. Le travail des élèves se fait à rebours de celui du constructeur.

La machine de Delaunay permet d’appliquer une dilatation à la figure de départ. Pour comprendre cela, on peut évoquer, outre des propriétés du losange, la similitude des triangles \(\mathsf{PQR}\) et \(\mathsf{CST}\) (figure 10).

Figure 10. La dilatation.

M. Maschietto suggère aussi d’inverser les rôles de la pointe sèche et du crayon ou de remplacer la pointe sèche par un crayon pour tracer deux figures en même temps. Ou encore de changer certains paramètres de la machine : longueurs des tiges, positions des points \(\mathsf{Q}\) et \(\mathsf{R}\) sur les tiges.

Modèles cosmologiques déduits des rayons solaires

Nicolas Décamp et Cécile de Hosson s’intéressent à la propagation de la lumière du soleil dans les modèles de cosmologie chinoise et grecque et dans l’imagination des élèves…

Problème 5. Ombres et modélisation

« Pour quelle raison aucune ombre n’est visible au pied des obélisques à Syène (…) à midi (…) alors qu’au même moment des ombres sont visibles au pied des obélisques à Alexandrie (…) ? » [1]

Produisez un dessin qui explique ce phénomène.

L’énoncé entre guillemets a été soumis à des élèves du cycle 3 (de 10 à 13 ans) en France. La plupart de ces élèves ont dessiné des rayons divergents tombant sur une Terre ronde ou plate. Et le phénomène s’explique dans les deux modèles.

Le chapitre dont est extrait ce problème présente des textes chinois traitant de ce sujet et propose de les utiliser en formation d’enseignants pour travailler la notion de modèle. L’étude des textes est accompagnée d’expérimentations. Les auteurs mettent aussi en perspective les cosmologies grecque et chinoise.

Bien d’autres situations sont étudiées dans Les mathématiques et le réel. Elles sont accompagnées d’une exploration d’écrits historiques et de réflexions épistémologiques sur l’enseignement, mais aussi d’idées d’utilisation en classe et de descriptions et d’analyse des expériences réalisées avec les élèves.

Références

[1] É. Barbin, D. Bénard et G. Moussard. Les mathématiques et le réel, expériences, instruments, investigations. Rennes : Presses Universitaires de Rennes, 2018.↩
[2] S. Stevin. Les oeuvres mathématiques de Simon Stevin. Leyde : Albert Girard, Bonaventure et Abraham Alsevier, 1634.↩
[3] C. É. L. Camus. Cours de mathématique, troisième partie. Éléments de méchanique statistique, tome II. Paris : Imprimerie royale, 1752.↩
[4] A. Manneson-Mallet. La géométrie pratique divisée en quatre livres. Livre III : La planimétrie. Paris : Anisson, 1702.↩
[5] N. Bion. Traité de la construction et des principaux usages des instruments de mathématiques. Paris : chez la Veuve Boudot, 1709.↩
[6] M. N. Delaunay. « Sur quelques nouveaux mécanismes ». In : Bulletin des sciences mathématiques (1702), pp. 193-204.↩