Une relecture des structures multiplicatives
de Gérard Vergnaud à travers le regard
de la modélisation

Difficile d’aborder un fil rouge sur la multiplication sans parler des structures multiplicatives de Vergnaud. Richard Cabassut les envisage ici à travers le regard de la modélisation. Un article de didactique à la portée de tous.

Richard Cabassut

© APMEP Septembre 2018

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Nous n’étudierons pas ici de manière approfondie la modélisation [3] ou la théorie de Vergnaud : le lecteur intéressé pourra se plonger dans des études plus savantes [7].Notre intention est de mettre en relation les structures multiplicatives de Vergnaud avec les considérations des programmes de 2016 sur la modélisation.

La modélisation pour les structures multiplicatives

Le rôle de la modélisation dans les programmes

Dans son ouvrage L’enfant, la mathématique et la réalité [14] (quatrième de couverture), dès 1981, Vergnaud « analyse les problèmes posés par l’enseignement des mathématiques à l’école élémentaire et décrit de manière détaillée différentes étapes et différents aspects du processus de mathématisation du réel ». Or dans les nouveaux programmes de la scolarité obligatoire de 2016, mathématiser, c’est-à-dire modéliser avec les mathématiques, apparaît comme l’une des six compétences majeures des mathématiques. Cette compétence est décrite comme suit dans le BOEN [2] : «

• Utiliser les mathématiques pour résoudre quelques problèmes issus de situations de la vie quotidienne.

• Reconnaître et distinguer des problèmes relevant de situations additives, multiplicatives ¹, de proportionnalité.

• Reconnaître des situations réelles pouvant être modélisées par des relations géométriques (alignement, parallélisme, perpendicularité, symétrie).

• Utiliser des propriétés géométriques pour reconnaître des objets. »

En cycle 4 :  «

• Reconnaître des situations de proportionnalité et résoudre les problèmes correspondants.

• Traduire en langage mathématique une situation réelle (par exemple à l’aide d’équations, de fonctions, de configurations géométriques, d’outils statistiques).

• Comprendre et utiliser une simulation numérique ou géométrique.

• Valider ou invalider un modèle, comparer une situation à un modèle connu (par exemple un modèle aléatoire). »

La compétence modéliser est une compétence transversale présente dans toutes les disciplines : « L’abstraction et la modélisation sont bien plus présentes désormais, ce qui n’empêche pas de rechercher les chemins concrets qui permettent de les atteindre. Toutes les disciplines y concourent : il s’agit de former des élèves capables de dépasser le cas individuel, de savoir disposer d’outils efficaces de modélisation valables pour de multiples situations et d’en comprendre les limites ».

Un document ressource de ces programmes [10] décrit « de manière schématique le processus de modélisation en distinguant trois temps : la mise au point d’un modèle à partir du réel, le fonctionnement du modèle lui-même à l’intérieur des mathématiques, et la confrontation des résultats du modèle au réel ».

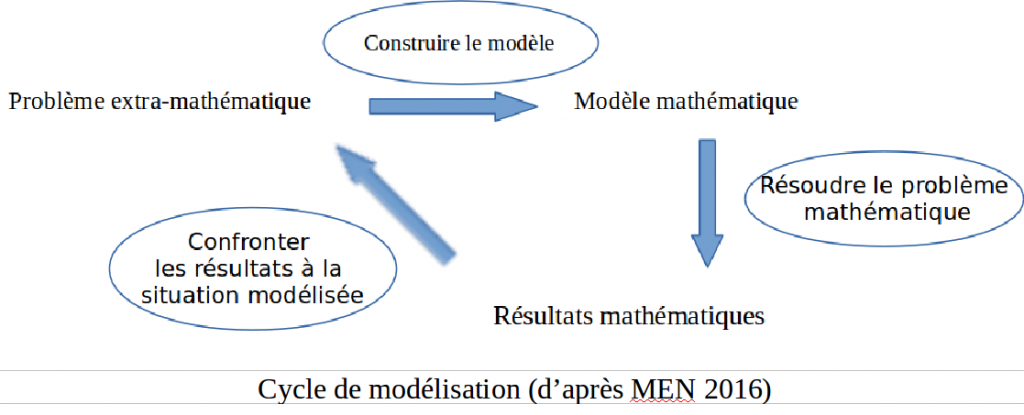
Les structures multiplicatives de Gérard Vergnaud

Dans les programmes précédents, on a remarqué que les situations multiplicatives sont évoquées explicitement pour mettre en œuvre la compétence de modélisation. « Le champ conceptuel des structures multiplicatives est à la fois l’ensemble des situations dont le traitement implique une ou plusieurs multiplications ou divisions, et l’ensemble des concepts et théorèmes qui permettent d’analyser ces situations : proportion simple et proportion multiple, fonction linéaire et \(n\)-linéaire, rapport scalaire direct et inverse, quotient et produit de dimensions, combinaison linéaire et application linéaire, fraction, rapport, nombre rationnel, multiple et diviseur, etc. » [13] (p. 147). Vergnaud distingue les problèmes multiplicatifs simples, dont nous allons rappeler les principales classes, et les problèmes complexes, qui peuvent coexister avec plusieurs problèmes multiplicatifs simples ou avec des problèmes d’autres types. Vergnaud considère principalement deux grandes catégories de modèles multiplicatifs simples : les isomorphismes de mesures avec les tableaux de proportionnalité à quatre éléments qui représentent une relation quaternaire, et le produit de deux mesures qui représente une relation ternaire. Décrivons d’abord ces grandes catégories de modèles multiplicatifs à construire pour résoudre un problème multiplicatif, puis nous préciserons ensuite quels traitements mathématiques (procédures de résolution) sont attendus pour chaque catégorie de modèle multiplicatif.

La construction d’un modèle pour les structures multiplicatives

Isomorphisme de mesures

Illustrons cette catégorie par le problème suivant : « J’achète 12 stylos à 1,50 € les 3. Combien dois-je payer ? »

Dans cette catégorie, quatre quantités sont en relation, deux concernent une sorte d’objets (les stylos), et deux une autre sorte d’objets (les euros).

On peut représenter cette situation par le tableau de proportionnalité suivant :

Ce tableau est un tableau de proportionnalité qui exprime la relation de proportionnalité entre deux espèces² de grandeur : la quantité de stylos \(s\) et la quantité d’euros \(e\) (qu’on appellerait le prix en euros correspondant). Le coefficient de proportionnalité \(k\) entre \(s\) et \(e\) est le prix unitaire d’un stylo et permet d’écrire la relation \(e = s \times k\).

On appelle parfois en mathématiques « recherche de la quatrième proportionnelle » le problème consistant, dans un tableau de proportionnalité à quatre éléments dont trois sont connus, à chercher le quatrième.

Vergnaud construit alors un isomorphisme de mesures entre l’ensemble des mesures de la première espèce de grandeurs (les stylos) et les mesures de la seconde espèce de grandeurs (les euros) qui à \(s\) associe \(k \times s\). Cet isomorphisme est une application linéaire (c’est-à-dire qu’il conserve l’addition interne et la multiplication externe). Il précise que dans cette représentation du problème par un tableau, on a une relation quaternaire entre quatre quantités (dans notre exemple : \(3\) ; \(1,50\) ; \(12\) ; \(x\)).

Ce qui nous paraît intéressant est la distinction avec le problème suivant.

« Pierre a 12 ans. Il pesait 15 kg à 3 ans. Combien pèse-t-il maintenant ? »

On pourrait représenter le problème par le tableau suivant³.

On pourrait construire une bijection entre l’ensemble des mesures de l’âge et l’ensemble des mesures du poids, mais cette bijection ne conserve pas l’addition et la multiplication externe car il n’y a pas proportionnalité entre l’âge et le poids.

Pour ce qui concerne le premier problème, c’est la connaissance des situations de la vie quotidienne, et de cette situation en particulier, qui permet d’affirmer qu’en général le prix payé est proportionnel à la quantité achetée, sachant que ce n’est pas toujours le cas. C’est donc une connaissance extra-mathématique qui amène à faire l’hypothèse de proportionnalité entre le nombre de stylos et le prix payé. Cette hypothèse est mathématique puisqu’elle porte sur un concept mathématique, la proportionnalité, dont on va utiliser les propriétés mathématiques dans la résolution du problème (linéarité…).

Pour ce qui concerne le second problème, ce sont des connaissances extra-mathématiques de santé sur l’indice de masse corporelle qui montrent, sur différentes courbes du poids en fonction de l’âge, que ces courbes ne représentent pas une relation de proportionnalité. On utilisera également des connaissances mathématiques pour vérifier que le non-alignement des points met en défaut la proportionnalité.

Finalement, des connaissances extra-mathématiques (pour reconnaître ou non une situation de proportionnalité entre deux espèces de grandeurs) et mathématiques (pour savoir que la proportionnalité détermine un coefficient de proportionnalité entre les mesures correspondantes des deux espèces de grandeurs) sont nécessaires.

Se pose donc la question de savoir si ces connaissances extra-mathématiques et mathématiques sont à la portée des élèves à qui ces problèmes sont proposés. Plus un contexte sera familier à un élève, plus facilement il mobilisera des connaissances offertes par le contexte familier pour résoudre le problème posé.

Au contraire la première rencontre avec un contexte mettra peut-être en évidence que l’élève ignore des connaissances extra-mathématiques (et éventuellement mathématiques) liées au contexte et nécessaires à une résolution du problème posé.

Coefficient multiplicatif dans un seul espace de mesures

Illustrons cette catégorie sur le problème suivant proposé par Vergnaud [14] (p. 179). « Il faut \(2\) mètres de tissu pour faire une jupe ; il en faut trois fois plus pour faire un ensemble. Combien de tissu faut-il pour faire un ensemble ? »

On peut représenter cette situation par le tableau suivant :

Par rapport au tableau de proportionnalité précédent, il n’y a plus qu’une espèce de grandeurs et il n’est pas évident que le coefficient multiplicatif serait conservé pour un même multiple de jupes et d’ensembles. De plus, le coefficient multiplicatif est ici un nombre, scalaire sans dimension, alors que le coefficient de proportionnalité du tableau précédent est le quotient de deux grandeurs.

Vergnaud parle d’opérateur-scalaire « (\(\times 3\) » dans notre exemple) dans ce cas, et d’opérateur-fonction dans le cas précédent (dans le cas des stylos et euros, \(\times 0,50\) est l’opérateur-fonction représentant le prix unitaire k du stylo évoqué précédemment.

Enfin, ici, la relation est ternaire : \(x = 2 \times 3\). On remarquera que des indices extra-mathématiques d’analyse du discours avec l’expression « 3 fois plus » peuvent orienter vers un modèle multiplicatif, même si l’on sait que pour certains élèves le « plus » peut renvoyer à l’addition. Nous détaillerons plus loin les différents types de problèmes associés à cette classe.

Le produit de mesures

Illustrons cette catégorie par le problème suivant : « On veut fabriquer des étiquettes. On peut réaliser 3 formes d’étiquette et utiliser 4 couleurs de papier. Combien d’étiquettes différentes⁴ peut-on réaliser ? »

Pour modéliser ce problème, on peut concevoir une étiquette comme un couple (forme ; couleur). Pour un nombre fini de formes \(F\) et un nombre fini de couleurs \(C\), on peut construire un tableau cartésien qui représente toutes les étiquettes possibles : on pourra alors dénombrer le nombre total \(E\) d’étiquettes. On peut représenter cette situation par le produit \(E = F \times C\) qui exprime la relation ternaire entre trois quantités \(E\), \(F\) et \(C\), où \(F\) est la mesure d’une première grandeur (ici la quantité de formes), \(C\) est la mesure d’une seconde grandeur (ici la quantité de couleurs) et \(E\) est la mesure d’une grandeur produit des deux grandeurs précédentes (ici \(E\) est la quantité d’étiquettes différentes).

Ce qui nous paraît intéressant est la distinction avec le problème suivant. « On veut fabriquer des étiquettes. On peut réaliser 3 formes d’étiquette et utiliser 4 couleurs de papier. Quel est le temps de fabrication des étiquettes ? »

Dans le premier problème, on peut considérer qu’une étiquette est caractérisée par sa forme et sa couleur et donc est assimilable à un couple (forme ; couleur). Une analyse de la situation nous amène à modéliser une étiquette comme un couple (forme ; couleur). On interprète d’autre part dans la question l’expression « étiquettes différentes » comme signifiant « étiquettes différentes par la forme ou la couleur ». En toute rigueur, en effet, si je découpe deux étiquettes de même couleur et de même forme, elles seront différentes, puisque je pourrais les tenir au même moment dans deux mains différentes. On voit donc que dans cette reconnaissance du modèle de produit de mesures interviennent des connaissances sur la situation réelle et sur la signification de l’énoncé.

Dans le second problème, on pose une question qui n’a rien à voir avec les données proposées pour vérifier quels sont les arguments qui justifient le choix d’un modèle. Ici il pourrait être tentant d’additionner ou de multiplier 3 et 4 entre eux, comme dans le problème de « l’âge du capitaine⁵ » [4].

Nous reviendrons dans la partie traitement mathématique sur comment dénombrer \(F \times C\).

Les autres classes

Nous n’aborderons que rapidement les autres classes de problèmes qui concernent les problèmes complexes de type multiplicatif pur ou de type mixte.

Illustrons par un exemple issu du projet LEMA [3] les problèmes complexes de type multiplicatif pur.

Dans une mise en œuvre en classe [11], une solution consiste à dénombrer sous certaines hypothèses le nombre de signatures en répondant à une série de questions se ramenant à des problèmes multiplicatifs simples : combien y a-t-il de signatures sur une feuille ? Combien de feuilles dans une rame de papier ? Combien de rames dans une caisse ? Combien de caisses dans un camion ? Combien de camions dans la rue ?

Un exemple de problème complexe de type mixte est illustré par l’exemple suivant :

« Sur l’autoroute, à l’entrée de Strasbourg, il y a eu un accident juste avant la sortie Baggersee. La circulation est bloquée entre les sorties voisines La Vigie et Baggersee. Combien de voitures sont bloquées ? » Pour la résolution de ce problème mis en œuvre en classe⁶, des structures multiplicatives sont mêlées à d’autres types de structures (comme par exemple les structures additives).

Dans ces problèmes complexes, on remarque l’importance des connaissances extra-mathématiques, et des hypothèses supplémentaires qui complètent la collecte des données utiles pour le modèle choisi, pour construire un modèle mathématique du problème réel proposé.

Examinons maintenant comment les différentes procédures de traitement mathématique des problèmes précédents permettent de définir des sous-classes de problèmes multiplicatifs.

Le traitement mathématique des problèmes multiplicatifs simples

Là où on pourrait ne distinguer que deux classes de problèmes, l’une associée à la multiplication \(x = a \times b\), l’autre associée à la division \(x = a \div b\), Vergnaud en distingue d’autres.

Les sous-classes de problèmes d’isomorphismes de structures.

Pour distinguer les différentes classes de problèmes relevant de l’isomorphisme de structures, Vergnaud considère des procédures de résolution du problème utilisées par des élèves et distingue quatre types principaux : la multiplication, la division-partition, la division-quotition et la quatrième proportionnelle.

La multiplication peut être représentée par le tableau de proportionnalité suivant :

Dans ce modèle, on connaît la valeur \(b\) de la mesure 2 correspondant à l’unité de la mesure 1.

Si \(c\) est entier, alors on introduit la multiplication comme addition itérée. \(c\) est donc \(c\) fois l’addition itérée de \(1\), et du fait de la linéarité additive liée à la proportionnalité, \(x\) est alors \(c\) fois l’addition itérée de \(b\), ce qu’on notera par x = b +  … + b, c  fois b ou encore x = b × c. Bien entendu les élèves de l’école primaire ne vont pas citer l’expression « linéarité additive » mais vont utiliser en acte cette propriété.

Si \(c\) est décimal ou fractionnaire, il faut étendre la propriété de linéarité additive à ces nombres.

La division-partition peut être représentée par le tableau de proportionnalité suivant :

Dans ce modèle, on cherche la valeur \(x\) de la mesure 2 correspondant à l’unité de la mesure 1 ; on dit parfois que \(x\) représente la valeur de la part. Dans le cas où \(c\) est entier, on est dans un problème de partage de \(d\) entre \(c\) éléments et on cherche la part \(x\) correspondant à chaque élément : la division-partition désigne donc un problème de partage (équitable) où on cherche la valeur de la part unitaire. On peut noter avec la notation précédente : d = x × c ou encore x = d : c. L’opérateur « \(\div c\) », qui fait correspondre \(c\) à 1 et \(d\) à \(x\) dans le tableau, est l’opérateur inverse de « \(\times c\) » qui fait correspondre \(1\) à \(c\) et \(x\) à \(d\). Cet opérateur « \(\div c\) » est un opérateur scalaire sans dimension que l’on exprime parfois par l’expression « c fois moins »: \(x\), c’est \(c\) fois moins que \(d\).

La division-quotition peut être représentée par le tableau de proportionnalité suivant :

Dans ce modèle, on cherche le nombre de parts \(x\) correspondant à \(d\), sachant qu’une part correspond à \(b\). On est donc dans un problème de partage de \(d\) en un nombre de parts \(x\), connaissant la valeur \(b\) d’une part : la division-quotition désigne donc un problème de partage (équitable) où l’on cherche le nombre de parts. On peut noter avec la notation précédente : \(d = b \times x\) ou encore \(x = d \div b\). L’opérateur « \(\div b\) » fait correspondre \(b\) à \(1\) et \(d\) à \(x\) : c’est l’opérateur inverse de « \(\times b\) » qui fait correspondre \(1\) à \(b\) et \(x\) à \(d\). Par rapport à l’opérateur précédent de la division-partition « \(\div c\) » qui était un opérateur scalaire sans dimension, ici l’opérateur « \(\div b\) » a la dimension quotient des dimensions de la mesure 2 par la mesure 1 (dans l’exemple des stylos et des euros, on diviserait des euros par un nombre de stylos).

La quatrième proportionnelle peut être représentée par le tableau de proportionnalité suivant :

Ce problème est un cas général du modèle de la multiplication, où \(a = 1\).

Une procédure possible à l’école primaire est de se ramener à un cas précédent où \(a = 1\) ; c’est la règle de trois ou règle de passage par l’unité⁷, décrite dans le tableau suivant :

On peut également utiliser directement un opérateur, comme suggéré dans les tableaux suivants :

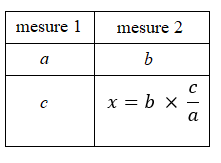
ou

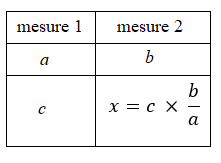
Bien entendu, au niveau du collège d’autres procédures pourront apparaître : « utilisation de l’égalité de rapports, utilisation de l’égalité des produits en croix, utilisation d’une représentation graphique » [8].

Les sous-classes de problèmes à coefficient multiplicatif dans un seul espace de mesures

Nous avons vu précédemment que cette situation peut être représentée par le tableau qui peut être résumé par la relation ternaire : \(b = a \times c\).

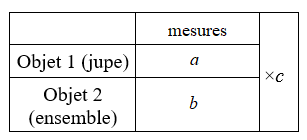
Trois modèles apparaissent suivant le nombre sur lequel porte la question :

• la multiplication

  

  Ce tableau peut être résumé par la relation ternaire : \(x = a \times c\).

  La question serait sur notre exemple : combien de tissu faut-il pour faire un ensemble ?

• la division – recherche d’une mesure :

  

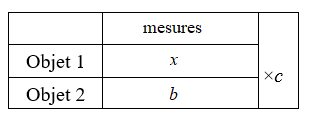
  Ce tableau peut être résumé par la relation ternaire : \(b = x \times c\).

  La question serait sur notre exemple : combien de tissu faut-il pour faire une jupe ?

• la division – recherche d’un scalaire :

  

  Ce tableau peut être résumé par la relation ternaire : \(b = a \times x\).

  La question serait sur notre exemple : combien de fois plus de tissu faut-il pour faire un ensemble par rapport à une jupe ?

Les sous-classes des problèmes produits de mesures

On peut représenter cette situation par le produit \(H = F \times G\), où \(F\) est la mesure d’une première grandeur, \(G\) est la mesure d’une seconde grandeur et \(H\) est la mesure d’une grandeur produit des deux grandeurs précédentes.

Deux modèles apparaissent suivant le nombre sur lequel porte la question :

• la multiplication : \(X = F \times G\) où l’on cherche la mesure produit connaissant les mesures élémentaires ;

• la division : \(H = F \times X\), où l’on cherche une des mesures élémentaires connaissant la mesure produit et l’autre mesure élémentaire et qu’on peut représenter par \(X = H\div F\).

Pour trouver le nombre de couples, on peut effectuer un dénombrement des cases du tableau cartésien qui les représente, ou bien effectuer une addition itérée du nombre de couples par colonne, ou une addition itérée du nombre de couples par ligne.

On notera que dans ces modèles de la multiplication, si on admet que le nombre de couples de \(F \times G\) est le même que le nombre de couples de \(G \times F\), alors la commutativité de la multiplication apparaît plus naturelle que dans la multiplication des isomorphismes de mesures ou dans le coefficient multiplicatif d’un seul espace de mesure, dans laquelle le multiplicateur, coefficient de proportionnalité ou coefficient multiplicatif, a un statut très différent de celui du multiplicande.

Passages d’une classe à l’autre

On peut remarquer que ces classes de modèles ne sont pas disjointes.

L’exemple précédent relevant du modèle multiplication dans la classe des isomorphismes de mesures, représenté par une relation quaternaire :

qui peut être résumé par la relation quaternaire : \(x = 12 \times \dfrac{1,50}{3}\) peut être représenté par un modèle de coefficient multiplicatif dans un seul espace de mesures :

qui peut être résumé par la relation ternaire : \(x = 1,50 \times 4\).

Mais on peut aussi interpréter l’égalité \(x = 12 \times \dfrac{1,50}{3}\) comme un produit de deux mesures : \(12\) est la mesure du nombre de stylos (première grandeur), \(\dfrac{1,50}{3}\) est la mesure du prix unitaire d’un stylo, c’est-à-dire de la mesure de la grandeur quotient prix payé par nombre de stylos, et \(x\) est la mesure du prix total payé, qui peut être interprétée comme le produit des deux mesures précédentes.

Enseignement de la modélisation des problèmes multiplicatifs

Nous n’avons qu’effleuré les difficultés des problèmes complexes : leur décomposition en problèmes simples réunit les difficultés de chaque problème simple et exige de surmonter les difficultés à décomposer puis recomposer ces différents problèmes. Nous nous limiterons donc ici à la considération des problèmes multiplicatifs simples exposés précédemment.

Concernant les spécificités de chaque classe de problèmes multiplicatifs, « la distinction de ces différentes classes et leur analyse doivent être soigneusement abordées afin d’aider l’enfant à reconnaître la structure des problèmes et à trouver la procédure qui conduira à leur solution. Il ne faut pas sous-estimer la difficulté de certaines notions comme celle de rapport, de proportion, de fraction et de fonction qui appellent des précautions didactiques importantes bien au-delà de l’enseignement élémentaire » [14] (p. 180). C’est pourquoi la classification de Vergnaud permet d’analyser les difficultés suivant la classe de modèle reconnue, en les repérant dans la procédure attachée à la classe et dans les notions sous-jacentes.

Il existe des difficultés communes à toutes les classes sur les notions suivantes :

• Les représentations utilisées pour la tâche initiale (texte énoncé écrit, texte énoncé oralement, photo mise à disposition…) et pour le modèle (tableau de proportionnalité, tableau cartésien, schéma fléché représentant les opérateurs scalaires ou fonctions…),

• Le contexte de la situation : sa familiarité rendra par exemple des connaissances extra-mathématiques davantage disponibles ; au contraire une dimension affective peut être un obstacle à une représentation détachée.

• L’ouverture de la situation : il peut être déstabilisant pour certains élèves de fréquenter des problèmes, où de nouvelles connaissances (ici sur la multiplication) vont être introduites. Dans les énoncés proposés pour les problèmes simples, la difficulté est de construire pour la première fois un modèle multiplicatif, ou de le reconnaître s’il a déjà été rencontré. Il semble raisonnable de se concentrer sur la construction d’un modèle et de laisser les hypothèses (par exemple de proportionnalité) ouvertes. Dans les problèmes plus complexes, la recherche des données utiles, des hypothèses nécessaires à la construction du modèle, voire des questions, peut être plus ouverte. On prendra cependant garde à ce que le problème ne soit pas fermé, en proposant dans son énoncé le modèle à appliquer : dans ce cas il ne s’agit plus d’un problème de modélisation mais d’un problème d’application.

  Un problème de partage équitable en début de CP pourra apparaître ouvert quant à la procédure de résolution : les élèves ne disposent pas encore de la division et vont probablement procéder par distribution. Ce même problème proposé en collège sera davantage fermé car les élèves ont connaissance de la procédure experte de la division et vont sans doute appliquer cette procédure.

  Il semble important de distinguer la nature des arguments pour construire le modèle :

• les arguments extra-mathématiques. Par exemple, on paie proportionnellement à la quantité achetée à la boulangerie de mon quartier, ce qui est une connaissance sociale,

• les arguments mathématiques. Par exemple, sur les différentes observations dans la boulangerie, les points représentant la somme payée en fonction de la quantité achetée sont alignés sur une droite passant par l’origine donc on peut supposer que le prix payé est proportionnel à la quantité achetée. Il se peut ultérieurement que le boulanger offre un croissant pour une quantité achetée importante et donc que l’hypothèse de proportionnalité devienne incorrecte : mais elle aura été formulée sur la base d’arguments mathématiques.

De même, pour construire le modèle, il semble important de distinguer les données utiles et les données inutiles issues de la situation, et les hypothèses supplémentaires que le modélisateur formule pour justifier son modèle. Tant qu’on n’a pas choisi un modèle, a priori on ne peut pas savoir si une donnée est utile au modèle choisi.

Dans cette phase de construction du modèle, on travaille essentiellement, dans la compétence modéliser, la reconnaissance de situations multiplicatives évoquée précédemment.

Soulignons l’importance des arguments mathématiques et extra-mathématiques qui justifient la reconnaissance du modèle. C’est dans cette phase de construction que le modèle multiplicatif doit acquérir du sens : aller trop vite dans le traitement mathématique du modèle, en donnant une trop grande importance à la maîtrise technique d’un algorithme opératoire au détriment de la justification du modèle choisi, risque d’évacuer trop vite ce sens, et d’aboutir à des phénomènes du type « âge du capitaine » ou « je n’ai pas compris ».

En négligeant la justification du choix du modèle qui apparaîtrait comme allant de soi, on risque de renforcer certains modèles qui sont naturalisés et deviennent dominants, par exemple l’équiprobabilité [5] ou la proportionnalité [1].

Vergnaud décrit « différents aspects du processus de mathématisation du réel, par lequel on peut conduire l’enfant à donner du sens aux concepts mathématiques et à en comprendre les propriétés » [14] (quatrième de couverture). Il s’agit donc bien de se placer du point de vue de la compréhension de l’élève et pas du seul point de vue de l’organisation mathématique. Par exemple, la propriété de commutativité de la multiplication peut être imposée dès le début dans une construction de l’organisation mathématique de la multiplication. Par contre, dans l’enseignement, si l’on souhaite construire une connaissance nouvelle sur la multiplication, à partir de connaissances anciennes sur l’addition par exemple, on peut opter pour une introduction de la multiplication comme addition itérée, comme évoqué dans notre exemple précédent sur le modèle de la multiplication dans le cas des isomorphismes de mesures. La reconnaissance de la commutativité de la multiplication, non naturelle dans ce cas, devra être justifiée. Ici, la nécessité de donner du sens aux concepts mathématiques et de comprendre les propriétés peut expliquer parfois le décalage entre l’organisation didactique et l’organisation mathématique. Actuellement la méthode d’enseignement de Pen Yee Lee [12] est promue par le Ministère de l’Éducation et certains membres de la Mission mathématique Villani-Torossian préconisent un retour à un enseignement transmissif et directif à l’ancienne : il serait intéressant d’étudier en quoi ces changements permettent aux élèves de donner du sens aux concepts mathématiques et de conforter la compétence de modélisation.

Conclusion

Nous avons rappelé la théorie de Vergnaud sur les structures multiplicatives en la regardant du point de vue de la modélisation. Sur le plan didactique, la relation quaternaire de la classe des isomorphismes de structures innove par rapport à la relation ternaire des autres classes. L’analyse des procédures sous-jacentes à chaque classe permet de repérer pour l’enseignement les points de difficultés et les notions mises en valeur. L’analyse dimensionnelle est une contribution importante au domaine « grandeurs et mesures » remis en valeur dans les programmes actuels.

Au lieu de se limiter au seul traitement mathématique, et souvent dans ce traitement aux seuls algorithmes de calcul, cette théorie permet de mieux différencier l’extra-mathématique du mathématique dans les différentes phases d’un processus de modélisation. Concrètement, il faut accorder plus de place à la discussion sur le choix des modèles, ce qui suppose une plus grande fréquence de problèmes ouverts. Dans la phase de résolution du problème mathématique, qui n’est pas spécifique à la modélisation, il faut également accorder davantage de place à la discussion des différentes procédures de résolution, en valorisant à la fois les procédures transférables qui pourront déboucher sur des méthodes, et les procédures qui illustrent davantage des stratégies et des heuristiques, notamment dans les problèmes atypiques qui ne débouchent pas toujours sur des procédures expertes. Bien entendu, il faut garder une place pour l’entraînement à la reconnaissance des modèles de références, et aux techniques de résolutions de ces problèmes. On voit la difficulté pour l’enseignement de ménager dans le temps une place pour ces différents moments. Évoquer les difficultés et les questions sur l’enseignement de la modélisation serait l’objet d’un autre article. Quels modèles de référence sont disponibles ? Quels modèles de référence sont à rendre disponibles ? Dans le curriculum, quelles programmations dans l’institutionnalisation des modèles de références ? Autant de questions à approfondir dans la formation et dans la production de ressources [6].

Références

1. R. Adjiage et M. Weisser. « Étude comparée de deux pratiques enseignantes lors d’une séquence de résolution d’un problème de modélisation. » In : Éducation & Didactique 7 (2013), p. 55–78.↩

2. BOEN. « Programmes d’enseignement du cycle des apprentissages fondamentaux (cycle 2), du cycle de consolidation (cycle 3) et du cycle des approfondissements (cycle 4) ». In : Bulletin officiel spécial 11 du 26 novembre 2015. (2015).↩

3. R. Cabassut. « Des ressources pour enseigner la modélisation. Projet européen LEMA. » In : Bulletin vert de l’APMEP 491. 19 (2010).↩

4. Y. Chevallard. « Quel est l’âge du capitaine ? » In : Bulletin vert de l’APMEP 323. (1980), p. 235–243.↩

5. N. Gauvrit. « A propos du « biais d’équiprobabilité ». » In : Recherches en didactique des mathématiques. 33.2 (2013), p. 163–182.↩

6. O. Graff, Calmelet J.-J. et B. Wozniak. Situations multiplicatives – Problèmes de multiplication et de division. Canopé – CRDP de Lille, 2011.↩

7. J.P. Levain et A. Didierjean. « Problèmes multiplicatifs, proportionnalité et théorie des champs conceptuels. » In : Rééducation Orthophonique 269 (2017), p. 145–160.↩

8. Ministère de l’Éducation Nationale. « Proportionnalité au collège. Ressources pour les classes de 6e, 5e, 4e et 3e du collège. » In : Direction générale de l’enseignement scolaire – Bureau du contenu des enseignements. (2005).↩

9. Ministère de l’Éducation Nationale. « Grandeurs et mesures au collège. Ressources pour les classes de 6e, 5e, 4e et 3e du collège. » In : Direction générale de l’enseignement scolaire – Bureau du contenu des enseignements. (2007).

10. Ministère de l’Éducation Nationale. « Mathématiques. Compétences travaillées en mathématiques. Modéliser. Ministère de l’Éducation nationale, de l’Enseignement supérieur et de la Recherche.  ». In : Eduscol (2016).↩

11. V. Paillet. « Où sont les maths ? » In : Repères IREM 82 (2011), p. 5–21.↩

12. L. Pen Yee, L. Nghan Hoe et trad. Beaujard Marion. Méthode de Singapour / pratiques de classe. La librairie des écoles ( 2017).↩

13. G. Vergnaud. « La théorie des champs conceptuels. » In : Recherches en didactique des mathématiques 10.23 (1990), p. 133–170.↩

14. G. Vergnaud. L’enfant, la mathématique et la réalité. Berne : Editions Peter Lang (1981).↩

Richard Cabassut est membre de la régionale APMEP de Strasbourg, de l’équipe d’Au fil des maths, et enseigne à l’Université de Strasbourg.