Vers la trigonométrie

Henry Plane nous propose un bref survol historique sur les origines de la trigonométrie. Nous pourrons découvrir que des notions aujourd’hui équivalentes n’ont pas toujours, au même moment, joué le même rôle.

Henry Plane

© APMEP Juin 2019

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

On chercherait en vain le mot « trigonométrie » dans les traductions françaises de ce qui fut appelé « Géométrie d’Euclide », que ce soit celle réputée la plus ancienne imprimée (vers 1613) de Didier Dounot, celle que Pascal aurait lue en cachette de son père ou celle plus documentée de Peyrard (1819).

En effet, si cette géométrie construit des figures et étudie des rapports, elle ne cherche pas, connaissant trois éléments convenables déterminant un triangle et les ayant mesurés, comment calculer les mesures des trois autres. Cela était la tâche soit des astronomes — le triangle était sphérique — soit de ceux que les latins nommaient « agrimensores », arpenteurs, qui se voyaient confier cette tâche par des services de génie civil (cadastre) ou militaire.

Un premier problème se posait alors, lorsque les gens de cette science commencèrent à pratiquer, fin XVI^e siècle et surtout au XVII^e siècle, les calculs en système décimal. Les mesures d’arcs en système hérité de Babylone s’adaptaient assez facilement :

\(1\) degré \(=60\) minutes ;

\({0,1}\) degré \(=6\) minutes (\(0,1\text{º}=6′\)) ;

\(1\) minute \(=60\) secondes ;

\({0,01}\) degré \(=36\) secondes (\(0,01{º}=36″\)) ;

en revanche, il n’en allait pas de même pour les longueurs (il faudra attendre 1790 pour la création du système métrique et même 1840 pour que l’usage de celui-ci se répande) :

\(1\) toise \(=6\) pieds ;

\(1\) pied \(=12\) pouces ;

\(1\) pouce \(=12\) lignes ;

\({0,1}\) toise \(=7\) pouces \(2\) lignes et \(\dfrac{2}{5}\) ligne…

Toutefois le nombre des utilisateurs du calcul décimal ne va cesser de croître, en particulier pour ceux qui furent conduits à pratiquer ce qui fut d’abord la… triangulométrie.

Le problème de base est d’établir le lien entre arc et corde le sous-tendant, et de trouver un procédé fiable pour les mesurer. Il n’est pas défendu de penser que des premières tables furent empiriques, fruits de l’expérience, mais rapidement la géométrie apporta la rigueur par le jeu des polygones réguliers inscrits dans un cercle. Une figure joua alors un rôle primordial :

À l’angle \(\widehat{x\mathsf{O}y}\) ou à l’arc \(\overset{\displaystyle\frown}{\mathsf{AB}}\) correspondant, est associé le segment \([\mathsf{BM}]\) sur l’orthogonale à \((\mathsf{OA}\)) menée par \(\mathsf{B}\) et qui recoupe le cercle en \(\mathsf{C}\).

\((\mathsf{OA}\)) est médiatrice de \([\mathsf{BC}]\), \(\mathsf{BC}=2\mathsf{BM}\) et l’arc \(\overset{\displaystyle\frown}{\mathsf{BC}}\) vaut deux fois l’arc \(\overset{\displaystyle\frown}{\mathsf{BA}}\).

On retint : \(\mathsf{BM}\) moitié de la corde sous-tendant l’arc double de l’arc \(\overset{\displaystyle\frown}{\mathsf{BA}}\).

Pourquoi la longueur de \([\mathsf{BM}]\) reçut-elle le nom de sinus de l’angle \(\widehat{x\mathsf{O}y}\) ou de l’arc \(\overset{\displaystyle\frown}{\mathsf{AB}}\) ?

De la Caille, membre de nombreuses académies des sciences (Paris, Berlin, Saint Petersbourg) et très impliqué dans des travaux d’astronomie et de géodésie (mesure d’un degré de méridien au Cap) nous en donne une explication dans ses « Leçons de géométrie » (1741).

On notera qu’en espagnol cette ligne est appelée « seno » et qu’il est écrit \(\mathrm{sen}(\widehat{\mathsf{AOB}})\).

En anglais on écrit \(n(\widehat{\mathsf{AOB}})\) mais il s’agit de l’abréviation de \(\mathrm{sine}(\widehat{\mathsf{AOB}})\), bien distinct du « sinus » qui désigne encore aujourd’hui la cavité de l’os frontal.

Dès la fin du XVI^e siècle, ce sont les polygones réguliers inscrits dans le cercle qui font le lien entre mesures de l’arc et de la corde. Cela va donner naissance à tout un vocabulaire, des notations et des méthodes de calcul qui ne sont encore qu’une sorte de triangulométrie.

On précisera :

\(\mathsf{MB}\) : sinus droit ; \(\mathsf{MA}\) : sinus verse ; \(\mathsf{AT}\) : tangente ; \(\mathsf{OT}\) : sécante pour la mesure des segments correspondants, le rayon OA étant pris pour unité.

Mais les calculs sont lourds. On peut en juger par l’extrait suivant de formulaire :

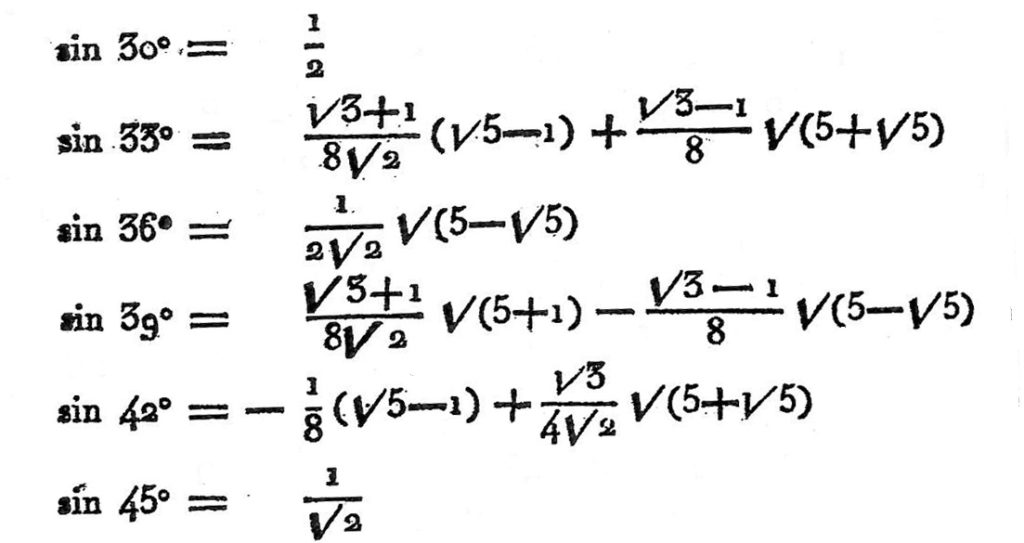
Pour obtenir une valeur approchée de ces lignes, il ne faut pas oublier que, en système décimal, le calcul d’une racine carrée demande de partir d’un nombre connu avec le double de décimales de celui du nombre attendu.

C’est pourquoi l’arrivée des logarithmes, en particulier ceux de Neper (John Napier, 1614), la publication de tables de logarithmes décimaux (Henry Briggs) et, surtout celles ainsi calculées, des lignes trigonométriques (Gunther, 1620) vont faciliter la tâche.

C’est alors qu’Henrion, qui a déjà donné en 1615 une traduction française des « Quinze livres de la géométrie d’Euclide », publie en 1623, à l’intention des officiers du roi, des « Mémoires mathématiques » contenant une « table des sinus, tangentes et sécantes » de minute en minute d’arc.

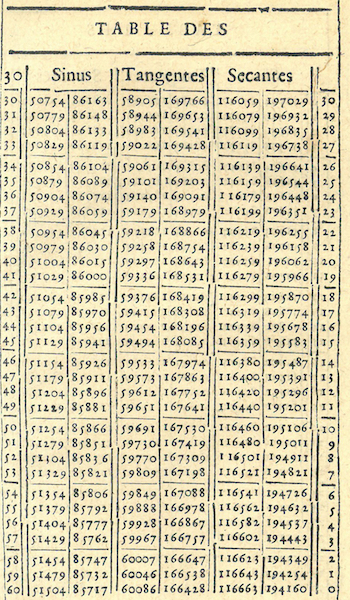
Le rayon du cercle est supposé de 100 000 parties, ce qui évite de s’appuyer sur le système décimal, légalement obligatoire mais encore peu répandu.

Dans cette page de l’ouvrage — où il n’y a pas d’abréviation — les relations entre arcs complémentaires sont bien utilisées.

Sinus du complémentaire d’un arc ? En latin, car celui-ci se pratique encore, c’est complementariis sinus, qui s’abrégera en co-sinus puis cosinus à la fin de ce XVII^e siècle.

D’autres propriétés sont mises en avant :
\(n(180-x)=n(x)\) ; et s’algébrisent :
\(n(-x)=-n(x)\) ; \(n(180+x)=-n(x)\).

On notera que le symbole \(\pi\) et les mesures en radian vont encore attendre un bon siècle.

Dès le début du XVIII^e siècle, tous les géomètres s’intéressent à ce rameau de la science.

Maintes « formules » surgissent que l’on retient : \(n(a+b)=n(a)\cos(b)+n(b)\cos(a)\) que l’on apprend et fait apprendre…

La notion de fonction prime alors. Sinus et cosinus en sont : continuité, parité, etc.

À ce sujet, on relira avec intérêt l’article « Les formules de trigonométrie sans pleurs » de Jean-Baptiste Hiriart-Urruty [1].

Viennent les développements :

\[n(x)\approx x-\frac{x^3}{3\, !}+\frac{x^5}{5\, !}+\cdots+\frac{(-1)^nx^{2n+1}}{(2n+1)\, !}\]

et dans un autre domaine : \(n(x)=\dfrac{\text{e}^{\text{i}x}-\text{e}^{-\text{i} x}}{2\text{i}}\cdotp\)

Au XIX^e siècle, les séries trigonométriques, ainsi que les séries de Fourier pour d’autres développements, dominent ce chapitre. On est loin de « la cognoissance très utile et nécéssaire aux choses géométriques » que préconisait Henrion dans ses « Mémoires mathématiques ».

Et maintenant ? Depuis la fin du XX^e siècle, la moindre calculatrice d’un élève de lycée a dans les replis cachés (en latin : sinus !) de son mécanisme tout ce dont on a besoin pour les calculs trigonométriques. Démontrer des formules de trigonométrie constitue dorénavant une nouvelle classe de problèmes.

Référence

1. Jean-Baptiste Hiriart-Urruty. « Les formules de trigonométrie sans pleurs ». In : Bulletin de l’APMEP n^o 515 (septembre-octobre 2015). ↩

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Henry Plane, professeur de mathématiques retraité, est un membre actif de l’APMEP. Il appartient au groupe M :ATH (Mathématiques : Approche par des Textes Historiques) de l’IREM de Paris VII.