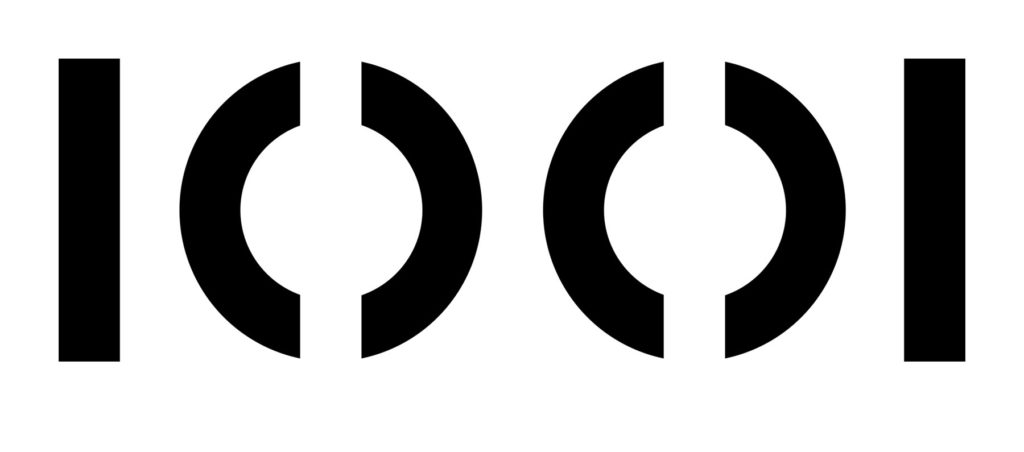 , vous avez dit
, vous avez dit 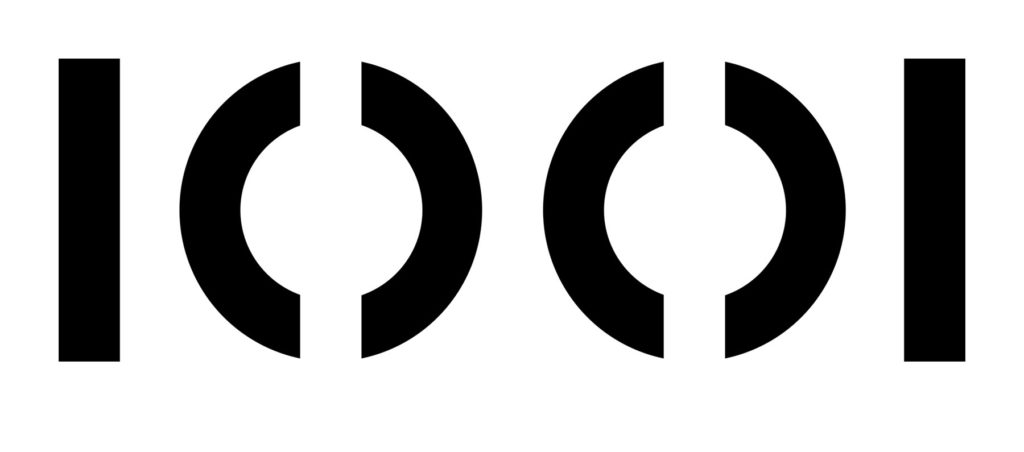 ?
?

© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Continuer la lecture de 1 001, vous avez dit 1 001 ?
© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Continuer la lecture de 1 001, vous avez dit 1 001 ?Continuer la lecture de N° 537 : Mathématiques et arts
© APMEP Juin 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Continuer la lecture de Le bridge à l’école : un compte-rendu d’expérience
© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Continuer la lecture de Le pourquoi et le comment
© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Continuer la lecture de Le musée de JSM
© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Continuer la lecture de La magie des azulejos
© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Continuer la lecture de Qui a (vraiment) le pouvoir au Parlement ?
© APMEP Juin 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Continuer la lecture de Faire du calcul mental en jouant avec Chamboul’math
© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Mathématiques et Arts, à première vue, rien à voir… Pourtant, les liens entre ces deux manières de dire le monde sont beaucoup plus profonds qu’on ne le croit. Leur relation est intime, vous en serez convaincus en lisant ces pages. Le calcul, réputé froid et ennuyeux, ne s’oppose pas à la liberté de l’artiste, il ne l’entrave même pas. L’imagination sans la rigueur termine en élucubration, la rigueur sans l’imagination dégénère en raideur.
D’ailleurs, il y a une esthétique dans les mathématiques, accessible à tous par la beauté de certaines formes géométriques ou courbes paramétrées. Mais il y a aussi une esthétique spécifique, propre aux mathématiques, qui va se nicher dans ce que nous appelons une «belle démonstration» ou une « jolie formule », où semble atteinte une certaine perfection dans le dépouillement et l’efficacité. Il faut y voir un effet de l’art, dépassant l’artisanat de l’activité mathématique.
Pour tout dire, rajoutons que, tout comme les mathématiques, l’art ne tire son génie créateur que d’une alliance entre une patiente pratique et une imagination féconde. Et notre discipline ne se laissant pas ranger facilement dans la Science, on peut bien lui faire, à l’instar des Grecs, une place de choix au milieu des Arts. Alors, Maths et Arts, bien sûr!
Au plus près du quotidien de notre métier, l’association « Les Maths en scène » ![]() , une de nos partenaires, a lancé le projet «Regards de géomètre». Ce projet a pour objectif de faire découvrir la culture mathématique via le monde artistique et scientifique pour des élèves de la maternelle jusqu’au lycée. Vous pourrez retrouver sur leur site de nombreuses productions d’élèves. Nous sommes attachés à ces projets qui permettent de travailler autrement les mathématiques et qui aident à leur trouver du sens. La géométrie n’est pas le seul exemple du rapprochement entre maths et arts. On peut facilement penser à la musique, mais n’oublions pas la littérature… Je vous invite à lire ou relire l’article de Rémi Duvert, Mathématiques et littérature
, une de nos partenaires, a lancé le projet «Regards de géomètre». Ce projet a pour objectif de faire découvrir la culture mathématique via le monde artistique et scientifique pour des élèves de la maternelle jusqu’au lycée. Vous pourrez retrouver sur leur site de nombreuses productions d’élèves. Nous sommes attachés à ces projets qui permettent de travailler autrement les mathématiques et qui aident à leur trouver du sens. La géométrie n’est pas le seul exemple du rapprochement entre maths et arts. On peut facilement penser à la musique, mais n’oublions pas la littérature… Je vous invite à lire ou relire l’article de Rémi Duvert, Mathématiques et littérature ![]() , pour vous convaincre des liens entre ces deux disciplines souvent séparées dans les cursus. Quant aux lectures et études des textes de l’OuLiPo
, pour vous convaincre des liens entre ces deux disciplines souvent séparées dans les cursus. Quant aux lectures et études des textes de l’OuLiPo ![]() , elles sont toujours l’occasion de faire des mathématiques et de la littérature en interdisciplinarité avec nos élèves tout en s’amusant.
, elles sont toujours l’occasion de faire des mathématiques et de la littérature en interdisciplinarité avec nos élèves tout en s’amusant.
À la lecture de ce numéro d’Au fil des maths, vous ne pourrez donc qu’aboutir à cette conclusion: il existe un isomorphisme entre artistes et mathématiciens… N’hésitez plus : faites des maths, soyez artistes !
Sébastien Planchenault
Président de l’APMEP
© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Continuer la lecture de Pour un droit aux mathématiques !