Petite enquête sur …
la logique dans la scolarité

Complément numérique

François Boucher

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Avertissement

Le début de l’article, concis et de lecture exigeante, se centre sur la construction de la logique pour en montrer les difficultés, notamment en terme de symbolique et de sémantique. La suite défend l’idée que c’est plutôt la construction du sens en mathématiques qui favorisera la compréhension de la logique chez les élèves enet non le contraire en l’illustrant par des exemples de mathématique scolaire.

Un contexte babélien

Le mot «logique» est souvent accompagné d’une kyrielle de qualificatifs dont il n’est pas simple d’identifier ce qu’ils qualifient vraiment : aristotélicienne, classique, symbolique, moderne, bivalente, formelle, contemporaine, modale, intuitionniste, dialogique, mathématique, linéaire … Tout cela est la marque de la diversité des corps de métier qui s’occupe de logique et donc de la diversité de leurs centres d’intérêt ; le domaine est en bonne santé et fort productif. Et depuis quelques décennies, la didactique s’en préoccupe. Mais pour l’enseignant de mathématiques néophyte et curieux, le brouillard peut sembler franchement épais.

La logique qui nous intéresse est celle qu’on peut qualifier à la fois de «moderne, standard, bivalente et mathématique», qui, sur la base des héritages grec, médiéval et arabe, s’est lentement élaborée à partir du XIX^e siècle, œuvre d’une longue lignée très internationale de mathématiciens philosophes de Bernard Bolzano (tchèque), Gottlob Frege (allemand), Bertrand Russell (britannique) à Alfred Tarski (polonais) pour ne citer qu’eux [1]. Depuis, la logique poursuit son développement mais dans des directions intéressant peu la scolarité¹.

Syntaxe

Précisons sommairement ce qu’il faut entendre par le caractère à la fois formel et formaliste de la logique dite «du premier ordre». Pour cela, nous allons un peu jouer à l’avocat du diable hilbertien au pays enchanteur d’Alice².

Pointons donc d’abord une faible loupe sur la syntaxe de $\mathbf{L}^0$, la partie de la logique dite «calcul des propositions». C’est d’abord un langage³ dans lequel on utilise des mots comme : $\neg p$ ou $p \Rightarrow q$ ou $(\neg p \Rightarrow p) \Rightarrow p$, mots formés à l’aide d’un alphabet de symboles distincts (en nombre non fini) $p,\,q,\,r,\ \ldots\ , p_1,\,q_1,\,r_1,\ \ldots$ et de deux constantes logiques $\neg$ («lire non»), $\Rightarrow$ («lire flèche») et de séparateurs (,) ; parmi tous les mots, on distingue — par une définition inductive (récursive) non précisée ici — les formules ou mots bien formés, les seuls qui font partie du langage. C’est le cas des mots à une lettre $p,\,q,\,r,\ \ldots\ $ (les atomes), de $\neg p$, de $p \Rightarrow q$, mais pas de $pqr$, ni de $r\neg$ ou de $\Rightarrow p\neg q$⁴.

Pour simplifier l’écriture et la lisibilité, on introduit des abréviations :

$p \vee q =_{\textrm{def}} \neg p \Rightarrow q$ $p \wedge q =_{\textsf{def}} \neg ( p \Rightarrow \neg q)$ $p \Leftrightarrow q =_{\textrm{def}} (p \Rightarrow q) \wedge (q \Rightarrow p)$.

Notons qu’il n’y a pas d’égalité dans $\mathbf{L}^0$ mais qu’elle est bien disponible dans le métalangage.

En s’appuyant sur la définition récursive des formules, il est possible d’écrire un programme python qui identifie si un mot donné est une formule ; on dit que «être une formule» est une propriété décidable.

Pour la suite, il est indispensable d’introduire des variables dites syntaxiques $A,\,B,\,C,\, \ldots$ qui seront utilisées comme noms de formules et ne font pas partie du langage $\mathbf{L}^0$ (et donc appartiennent au métalangage).

La deuxième étape est de construire un calcul sur les formules ; pour cela, on distingue parmi les formules de $\mathbf{L}^0$ les formules valides qu’on appelle aussi des théorèmes et un nouveau symbole $\vdash$ est introduit pour les désigner. Pour «produire des théorèmes», on peut :

$\bullet$ utiliser des schémas d’axiomes : il y en a trois ; citons le plus simple : $A \Rightarrow (B \Rightarrow A)$ ⁵. Comme en mathématiques, par exemple en théorie des groupes, les axiomes définissent implicitement les constantes logiques $\neg$ et $\Rightarrow$. Précisons que, dans un schéma d’axiomes, on peut substituer aux variables syntaxiques une formule quelconque et obtenir un théorème ; utiliser un tel schéma évite de formuler des règles de substitutions délicates à utiliser. Un schéma d’axiomes condense donc une infinité d’axiomes. Le lecteur avisé pourra se demander si cette façon de procéder ne cache pas une quantification.

$\bullet$ utiliser la (méta)règle de déduction (dénotée RD dans la suite) : si $A$ et $A \Rightarrow B$ sont des théorèmes alors $B$ est un théorème⁶.

L’écriture $\mathscr{T} \vdash A$ (lire «$\mathscr{T}$ prouve $A$» ou «$A$ se déduit de $\mathscr{T}$» ) dans laquelle $\mathscr{T}$ est un ensemble (éventuellement vide) de théorèmes et $A$ une formule signifie que $A$ est un théorème obtenu par applications itérées des deux procédés précédents à partir de $\mathscr{T}$, ce qui définit une démonstration dans $\mathbf{L}^0$.

Par exemple la règle de déduction s’écrit $\{A,\, A \Rightarrow B \} \vdash B$.

Autres exemples (pas simples) : $\vdash B \vee \neg B$ ou $\vdash A \Rightarrow A$. Détaillons la seconde :

$\vdash A\Rightarrow (B \Rightarrow A)$	axiome 1
$\vdash (A \Rightarrow (B \Rightarrow A)) \Rightarrow \left((A \Rightarrow B) \Rightarrow (A \Rightarrow A)\right)$	axiome 3
$\vdash (A\Rightarrow B)\Rightarrow (A\Rightarrow A)$	RD
$\vdash (A\Rightarrow (B \Rightarrow A))\Rightarrow (A\Rightarrow A)$	substitution (on comprend l’utilité de $B$)
$\vdash A \Rightarrow A$	RD

Il est clair que ce calcul n’a rien de mécanique, demande de l’expérience et une bonne capacité de raisonner par conditions suffisantes. Essayer de démontrer que $\vdash (A \Rightarrow B) \vee (B \Rightarrow A)$.

Le lecteur est en droit de se questionner sur l’utilité de ce calcul dans la classe de mathématiques ; il s’agit seulement de faire comprendre en quoi $\mathbf{L}^0$ est un calcul. On démontre d’ailleurs que être un théorème est aussi une propriété décidable.

Certains théorèmes, dignes d’intérêt, sont baptisés lois logiques comme :

$\vdash \left\{(A \Rightarrow B) \wedge (B \Rightarrow C) \right\} \Rightarrow (A \Rightarrow C)$ (transitivité de l’implication)

$\vdash A \Rightarrow (B \Rightarrow C) \Leftrightarrow (A \wedge B \Rightarrow C)$ (règle d’import-export)

$\vdash \left\{ \neg B \Rightarrow (C \wedge \neg C)\right\} \Rightarrow B$ (réduction à l’absurde)

toutes lois qu’Euclide utilisait naturellement comme d’ailleurs tout étudiant en mathématiques.

En anticipant sur la suite, pour démontrer un énoncé de la forme si $A$, alors si $B$, alors $C$ , un étudiant supposera $A$, puis supposera $B$ et démontrera $C$ sans avoir besoin de se référer à une loi logique.

Outre les théorèmes, l’intérêt des logiciens se porte sur les propriétés abstraites du langage $\mathbf{L}^0$. L’étude de ces propriétés (en particulier leur démonstration) relèvent d’une discipline particulière : la métalogique. Citons par exemple un théorème du à Jacques Herbrand (1908-1931), le théorème de la déduction :

$A \vdash B$ si et seulement si⁷ $\vdash A \Rightarrow B$

Il est temps d’arrêter le supplice ; le but des lignes qui précèdent est de montrer la grande difficulté qu’il y a à entrer dans un texte formel à moins d’être déjà familiarisé avec sa syntaxe, son usage et de pouvoir y greffer des significations. Lire «$p \Rightarrow q$» «$p$ implique $q$» plutôt que «$p$ flèche $q$» semble plus compréhensible car cela renvoie à du signifiant dans le langage courant et dans la pratique des mathématiques. Mais la logique, pour être formelle, ne se préoccupe pas des significations : a priori, «$p$» est juste un symbole qui ne signifie rien, pas plus que «$p \Rightarrow q$» : il est utile de voir ces mots comme des noms propres de propositions qui viendront à la réalité dans les interprétations futures. Et pour garantir la non-intrusion des significations parasites quoi de plus efficace que de formaliser totalement le langage ? C’est le travail qu’a réalisé Frege en imaginant son idéographie (1879).

Un point, assez négligé en mathématiques, mérite quand même attention : «$A \Rightarrow B$» est en général lu «$A$ implique $B$» mais cette phrase est assertive et signifierait donc «$\vdash A \Rightarrow B$» qui est différent de «$A \Rightarrow B$» : l’une est une proposition de $\mathbf{L}^0$, l’autre signe un théorème et appartient au métalangage et n’est plus une implication. Pour cette raison, les logiciens (non mathématiciens) renoncent à l’usage de $\Rightarrow$ et distinguent le conditionnel, dénoté plutôt par $\rightarrow$, et l’implication comme validité du conditionnel, dénotée plutôt par $\supset$, se montrant ainsi un cran plus formalistes : donc $A \supset B =_{\rm{def}}\ \vdash A \rightarrow B$. L’axiome cité ci-dessus se réécrit alors $A \supset (B \rightarrow A)$ … Maux de tête en perspective.

Dans [2], Marcel Condamine avait proposé l’écriture $A\raise5pt\hbox{$\displaystyle\bullet\atop\displaystyle\Longrightarrow$}B$ soulignant que c’est toujours $\raise5pt\hbox{$\displaystyle\bullet\atop\displaystyle\Longrightarrow$}$ qui est utilisé dans les textes mathématiques et jamais $\Rightarrow$.

La sémantique

Venons-en à ce que les logiciens appellent la sémantique de $\mathbf{L}^0$. La sémantique d’un langage est a priori l’étude (la théorie) des significations de ce langage. Il s’agirait donc de donner une signification aux formules, en particulier aux théorèmes. Du sens en perspective, donc ? À voir.

Appelons $\mathbb{A}$ l’ensemble des symboles (les atomes) et $\mathbb{F}$ l’ensemble des formules. Introduisons un ensemble à deux éléments, par exemple deux couleurs : $\mathbb{V}=\left\{\color{blue}{\clubsuit},\color{red}{\heartsuit}\right\}$⁸. Un coloriage d’une formule est l’attribution d’une couleur à chaque atome de la formule⁹. Par exemple (avec un abus d’écriture que ne s’autorisent pas les logiciens) $\color{blue}{\clubsuit} \Rightarrow (\color{red}{\heartsuit} \Rightarrow \color{blue}{\clubsuit}) $ est un coloriage de $p \Rightarrow (q \Rightarrow p)$ (il y en a trois autres)

Il s’agit ensuite d’attribuer une couleur globale à chaque formule coloriée de sorte que la couleur attribuée soit indépendante du coloriage dans le cas des théorèmes et en soit ainsi possiblement une signature. Privilégions, par exemple, $\color{blue}{\clubsuit}$. Mathématiquement, cela revient à définir, pour chaque $n$, une application de $\mathbb{V}^n$ dans $\mathbb{V}$ qui prend la valeur $\color{blue}{\clubsuit}$ sur les théorèmes à $n$ atomes.

La définition inductive des formules permet de comprendre (et de démontrer) qu’il suffit de définir la couleur de $\neg p$ (en fonction de celle de $p$) et la couleur de $p \Rightarrow q$ (en fonction de celles de $p$ et $q$) avec la condition nécessaire que, sur les axiomes, le coloriage fournissent bien la couleur $\color{blue}{\clubsuit}$.

$\neg \color{blue}{\clubsuit} = \color{red}{\heartsuit}$ et $\neg \color{red}{\heartsuit}= \color{blue}{\clubsuit}$ s’imposent facilement. Et pour $\Rightarrow$, le miracle¹⁰ se produit avec comme unique possibilité :

$\color{blue}{\clubsuit} \Rightarrow \color{blue}{\clubsuit}$	$\color{blue}{\clubsuit} \Rightarrow \color{red}{\heartsuit}$	$\color{red}{\heartsuit} \Rightarrow \color{blue}{\clubsuit}$	$\color{red}{\heartsuit} \Rightarrow \color{red}{\heartsuit}$
$\color{blue}{\clubsuit}$	$\color{red}{\heartsuit}$	$\color{blue}{\clubsuit}$	$\color{blue}{\clubsuit}$

On a alors : $\color{blue}{\clubsuit} \Rightarrow ( \color{red}{\heartsuit} \Rightarrow \color{blue}{\clubsuit}) = \color{blue}{\clubsuit}$.

Les tables de coloriage des autres connecteurs s’en déduisent. Il est donc possible d’attribuer à chaque formule, pour un coloriage donné, une couleur uniquement déterminée par ce coloriage ; mathématiquement, le coloriage des formules est une fonction. Reste à démontrer que la couleur d’un théorème est bien $\color{blue}{\clubsuit}$ comme désiré¹¹. Est ainsi définie ce qu’on appelle une sémantique bicolorée 🙂 (les logiciens disent bivalente) de $\mathbf{L}^0$ ; et cette sémantique est colorifonctionnelle 🙂🙂.

En construisant la table de coloriage de $p \Rightarrow (q \Rightarrow p)$, le lecteur pourra vérifier que sa couleur est bien constante égale à $\color{blue}{\clubsuit}$.

Si, pour un coloriage donné, la couleur d’une formule est $\color{blue}{\clubsuit}$, on dit que le coloriage est un modèle de la formule. Étant donnée une formule $A$, on dit que $A$ est logiquement valide (relativement à la sémantique ; «sémantiquement valide» serait appropriée) si et seulement si tout coloriage de $A$ en est un modèle, ce que l’on dénote par l’écriture $\vDash A$¹². On dit aussi bien que $A$ est une tautologie.

Exemples standards : $\vDash A \vee \neg A$ ou $\vDash \big((A \Rightarrow B) \wedge (\neg A \Rightarrow B)\big) \Rightarrow B$

Si tout modèle de $A$ est aussi un modèle de $B$, on écrit $A \vDash B$ (lire «$A$ valide $B$» ) ; si, de plus, réciproquement tout modèle de $B$ est aussi un modèle de $A$, on dit que $A$ et $B$ sont logiquement (sémantiquement) équivalentes. Ceci équivaut à $\vDash A \Leftrightarrow B$ qu’on écrit aussi $A \equiv B$ à rapprocher d’une remarque faite plus haut sur la différence entre le conditionnel et l’implication : $A \Leftrightarrow B$ diffère de $\vDash A \Leftrightarrow B$.

Exemple basique : $A \Rightarrow B \equiv \neg B \Rightarrow \neg A$

Signalons, avec un gros clin d’œil, une équivalence très utilisée par les mathématiciens depuis l’antiquité¹³ :

$\big((A \Rightarrow B) = \color{blue}{\clubsuit}\big) \equiv \left\{(A = \color{blue}{\clubsuit}) \Rightarrow (B = \color{blue}{\clubsuit})\right\}$

Cette sémantique est aussi formelle que la syntaxe associée. Et remplacer $\left\{ \color{red}{\heartsuit},\, \color{blue}{\clubsuit}\right\}$ par $\{\textrm{`0′ },\,\textrm{`1′}\}$ ou par $\{\textrm{`F’},\,\textrm{`V’}\}$, conformément à un usage bien établi (que nous allons adopter), pourrait nourrir le sentiment de porter une signification, mais il n’en est rien : dans chaque cas, on n’introduit que des valeurs formelles¹⁴. Le lecteur admettra certainement que la sémantique bicolorée présentée ci-dessus ne définit en rien la couleur bleue ou la couleur rouge. Rien ne serait changé en utilisant (, ).

La logique ne se préoccupe pas de dire ce qu’est la Vérité ; cette dernière n’est pas définissable en restant dans $\mathbf{L}^0$. Ceci ne peut se faire qu’à travers une interprétation (voir ci-après) faisant appel à un langage plus expressif que $\mathbf{L}^0$ : c’est la malédiction de Tarski [3].

Bien sûr, les logiciens historiques qui ont élaboré cette sémantique avaient bien à l’esprit de formaliser une théorie de la vérité utile aux philosophes, aux linguistes, et aux mathématiciens. Les traités de logique publiés récemment par des philosophe sont organisés autour de cette intention [4].

Terminons en revenant à une question de métalogique. On doit à Emil Post (1897-1954) le théorème dit de complétude qui vient peut être confirmer une intuition du lecteur sur le lien entre théorème et tautologie :

$\vdash A$ si et seulement si $\vDash A$

Ce théorème est de première importance car il assure une correspondante parfaite entre syntaxe (formelle) et sémantique (formelle). En particulier, la syntaxe qui définit axiomatiquement $\mathbf{L}^0$ contient sa bivalence.

À titre d’illustration simple mais efficace du théorème de Post, proposons une démonstration brève du théorème de la déduction. La version sémantique de l’équivalence «$A \vdash B$ si et seulement si $\vdash A \Rightarrow B$» est l’équivalence «$A \vDash B$ si et seulement si $\vDash A \Rightarrow B$». (On parle bien de méta-équivalence de méta-théorèmes !)

Par exemple, démontrons que, si $A \vDash B$, alors $\vDash A \Rightarrow B$. Par l’absurde : s’il n’est pas vrai que $A \Rightarrow B$ est une tautologie, c’est qu’il existe un coloriage de $A$ et $B$ tel que $(A \Rightarrow B)=\color{red}{\heartsuit}$ ; mézalor, d’après la table de couleurs de $\Rightarrow$, nécessairement $A=\color{blue}{\clubsuit}$ et $B=\color{red}{\heartsuit}$ ; en contradiction avec $A \vDash B$. Réciproque similaire.

Cette démonstration, typiquement mathématique, illustre au passage l’intérêt pour le logicien qui étudie les propriétés de $\mathbf{L}^0$ de la table complète de coloriage de l’implication ; et, en même temps, le lecteur aura aussi noté que c’est bien un «si vrai, alors nécessairement vrai» qu’on voulu démontrer et non pas une implication logique ce qui n’aurait ici pas de sens ; mais il s’agit du «vrai» de la métalangue (les mathématiques exprimées en français) et non pas du $\color{blue}{\clubsuit}$.

Ces quelques intrusions dans le calcul des propositions mettent en évidence la nécessaire utilisation d’une pré-logique (et d’une théorie naïve des ensembles) familière aux mathématiciens : l’usage dans la métalangue du «si … , alors …» , du «si et seulement si» , de «équivalent» de «il existe» ou de «tout» s’avère indispensable. Et plus important : l’utilisation des définitions inductives, pour les démonstrations de propriétés de $\mathbf{L}^0$, nécessite l’appel au raisonnement par récurrence dont la validation relève du calcul des prédicats … ! Mais, heureusement, cette métalogique n’utilise que des entiers «naïfs» ¹⁵ ; ouf !

Interprétations

Commençons par préciser de façon naïve l’idée d’interprétation d’une théorie formelle comme $\mathbf{L}^0$ dans un contexte mathématique de la scolarité comme $\mathcal{A}$ (algèbre) ou $\mathcal{G}$ (géométrie)¹⁶. On suppose un tel contexte non contradictoire et qu’on y est capable d’identifier le vrai et le faux (au sens usuel en mathématiques) des propositions.

Une interprétation de la sémantique de $\mathbf{L}^0$ dans une théorie consiste à construire un dictionnaire entre les objets de $\mathbf{L}^0$ et ceux de la théorie considérée de sorte qu’il y ait une bonne correspondance entre le $\color{blue}{\clubsuit}$ (respectivement le $\color{red}{\heartsuit}$) et le vrai (respectivement le faux) en particulier entre les tautologies de $\mathbf{L}^0$ et les théorèmes de la théorie.

Deux exemples suffiront :
$\bullet$ prenons pour théorie le corps à deux éléments $\left(\mathbb{Z}/2\mathbb{Z},\,\ + ,\, \cdot\right)$. On associe aux symboles $p,\,q,\,r, \cdots$ de $\mathbf{L}^0$ des variables $a,\,b,\,c, \cdots$ prenant leurs valeurs dans $\mathbb{Z}/2\mathbb{Z}$, à $\neg$ l’application $a \mapsto 1-a$ et au connecteur $\wedge$ l’opération $\cdot$. Ainsi la disjonction $p \vee q$ est associée à l’opération $a \oplus b = a+b-a\cdot b$ et l’implication $\Rightarrow$ est associée à l’opération $\require{upgreek} a\ i\ b = 1-a+a\cdot b$

$\vDash p \Rightarrow p$ correspond $1-a+a\cdot a=1$ (soit $a \cdot a =a$) et $\vDash p \Rightarrow (q \Rightarrow p)$ correspond $1-a+a\cdot (1-b + b\cdot a)=1$.

$\bullet$ prenons comme théorie l’algèbre de Boole $\left(\mathscr{P}(E),\,\Delta,\,\cap\right)$ où $E$ est un ensemble quelconque (fini ou non) ; soit $x$ un élément particulier de $E$. On associe aux symboles $p,\,q,\,r$ les propositions $x \in A$, $x \in B$, $x \in C$ où $A$, $B$, $C$ sont des parties de $E$ et à $\neg p$ la proposition $x \in \complement_E A$, à $p \vee q$ la proposition $x \in A \cup B$ et à $p \wedge q$ la proposition $x \in A \cap B$.

Cette interprétation est certainement la plus féconde et la plus utile si on a la scolarité en point de mire. On la trouve, bien sûr, à l’œuvre en probabilités.

Comment diluer $\mathbf{L}^0$ dans les mathématiques

Ce qui précède aide à percevoir le travail de transposition de la logique vers la scolarité, entrepris dans les années soixante, qui consiste d’abord à fusionner langue-objet, langue mathématique et langue courante, pratique habituelle en … mathématiques.

Ensuite, l’aspect syntaxique est mis de côté et l’entrée dans la logique des propositions se et fait par son versant sémantique mais en l’interprétant directement dans la langue courante ou dans celle d’un contexte mathématique, disons $\mathcal{T}$ ; le vocabulaire mathématique est substitué aux symboles logiques : non ($\neg$), et ($\wedge$), ou ($\vee$), équivaut ($\Leftrightarrow$), faux ($\color{red}{\heartsuit}$), vrai ($\color{blue}{\clubsuit}$) et si … alors … ($\Rightarrow$) : mais quel(s) si … alors … ?

Ensuite, à l’aide de l’alphabet de $\mathbf{L}^0$, on attribue un nom aux propositions de $\mathcal{T}$, une proposition étant définie comme tout ce qui peut être vrai ou faux (renvoyant au sens de ces mots dans $\mathcal{T}$, sens supposé bien défini). Les connecteurs, qui sont a priori des opérateurs sur les propositions, sont introduits par les fameuses tables de vérité, ce qui revient à poser leur vérifonctionnalité¹⁷ de principe.

Ces dernières sont justifiables facilement pour la négation, la conjonction, la disjonction, la disjonction exclusive ou l’équivalence. Les langages de programmation utilisent ces tables pour manipuler les objets de type booléen avec toutefois des règles d’évaluation spécifiques.

Pour l’implication, plutôt qu’un parachutage de la table de vérité qui peut poser question, il est utile d’observer, avec Stephen Kleene (1909-1994)[5], que l’accord est acquis sur les deux premières lignes et pour les deux dernières (cas de la prémisse fausse), il est possible d’examiner toutes les possibilités restantes et de constater qu’il n’y a pas d’autre choix, sémantiquement parlant puisque c’est bien de cela qu’il s’agit. En citant Patrick Dehornoy, c’est la moins mauvaise solution.

Ce qui apporte un peu de clarté, c’est d’interpréter les connecteurs comme des applications, au sens mathématique, de $\{V,\,F\}^2$ dans $\{V,\,F\}$.

Une conséquence s’impose alors : si on construit les tables de vérité de non($p$ et $q$) et de non($p$) ou non$(q$), l’identité des tables signe l’égalité des applications. Il est ainsi légitime d’écrire non($p$ et $q$) = non($p$) ou non$(q$). De même plus simplement non(non($p$)) = $p$. On dispose alors d’un calcul de nature algébrique (algèbre de Boole) qui a pu faire le bonheur des auteurs de manuels à une certaine époque.

On peut ensuite étendre la table de vérité à n’importe quelle proposition fabriquée en combinant négation et connecteurs selon une syntaxe intuitive mettant en jeu un nombre quelconque de lettres — mais rarement plus de trois — ce qui revient à définir une application de $\{V,\,F\}^n$ dans $\{V,\,F\}$.

En particulier, on dispose d’un moyen mécanique de déterminer la valeur de vérité de toute proposition complexe «décomposable» en propositions simples dont les valeurs de vérité sont connues. Une bonne question est alors : «cette observation a-t-elle un quelconque intérêt mathématique dans la scolarité ?»

Par exemple, dans $\mathscr{A}$ : $p$=«8767 est le carré d’un nombre entier» ou encore dans $\mathscr{G}$ : $q$ = «si le triangle $ABC$ est équilatéral, alors $\widehat{A}=60$» ; chacune est certainement vraie ou fausse au sens que prennent ces valeurs en mathématiques.

Pour savoir si ces propositions relèvent du calcul des propositions, ou plutôt pour savoir si ce calcul peut aider à répondre à la question de la vérité ou fausseté de ces deux propositions, il convient déjà de voir si elles sont atomiques ou composées (dans leur contexte). On peut naturellement proposer $q = (U \Rightarrow V)$ avec $U$ = le triangle $ABC$ est équilatéral et $V$ = $\widehat{A}=60$. $V$ est raisonnablement un atome de $\mathscr{A}$. Pour $U$, la définition d’équilatéral peut se traduire par :

$U=(AB=AC) \textrm{ et } (BA=BC) \textrm{ et } (CA=CB)$

qui fournit une décomposition en atomes. $\mathbf{L}^0$ a produit ce qu’il pouvait produire et n’a plus rien à dire à l’élève chercheur qui doit questionner sa connaissance des objets géométriques pour imaginer une proposition tiers utile.

Pour $p$, si on veut rester dans $\mathbf{L}^0$, avec une dose d’implicite ou d’intuition non formalisée et en supposant que l’algorithmique a une influence positive sur la pensée mathématique, on peut imaginer
$p=(8767>90^2) \textrm{ et } \left\{(8767=91^2) \textrm{ ou } (8767=93^2) \textrm{ ou } \ldots \textrm{ ou } (8767=99^2)\right\} \textrm{ et } (8767<100^2)$.

Un peu de patience fournit alors $p=$ faux. Auquel cas, il convient de proposer aussitôt le même problème avec $18446744073709551617$. Peut-on penser que ces interventions plutôt artificielles du calcul propositionnel soient utiles, voire possibles ? La résolution de problèmes doit-elle passer sous de telles fourches ? Comment le calcul des propositions pourrait-il guider vers une solution plus prometteuse consistant à s’intéresser au chiffre des unités, idée qui demande un «pas de côté» : accepter de perdre de l’information sur l’hypothèse ; une saine fréquentation de problèmes divers relatifs aux entiers a plus de chances d’y conduire.

Le calcul des prédicats : $\mathbf{L}^1$

Les prédicats s’avèrent inévitables dès qu’il s’agit d’analyser des propositions exprimant la généralité universelle (tous, tous sauf au plus un nombre fini, chaque, aucun) ou existentielle (quelque, certain, au moins un). Par exemple (avec des abus de langage usuels) :

$\bullet$ $p =$ «tout nombre se terminant par 5 a un carré qui se termine par 25» ;

$\bullet$ $q=$ «$F_5=2^{2^5}+1$ possède au moins un diviseur premier plus petit que 1000» ;

$\bullet$ $r =$ «aucun rationnel n’est solution de l’équation $x^3+x-3=0$» ;

$\bullet$ $s =$ «étant données deux droites distinctes de l’espace, il existe au moins une droite perpendiculaire à ces deux droites».

qui sont clairement des propositions de $\mathcal{A}$ ou $\mathcal{G}$. Aristote (IV^e siècle avant notre ère) avait introduit ce type de proposition «tout A est B» ou «quelque A est B» dans sa syllogistique. Ces propositions ne peuvent pas être analysées dans $\mathcal{A}$ en propositions plus simples ; pour la première, on pourrait bien envisager d’écrire une conjonction généralisée, quelque chose comme :

$p = (5^2=25) \textrm{ et } (15^2=\cdot25) \textrm{ et } (25^2=\cdot25) \textrm{ et } (35^2=\cdot\cdot25) \textrm{ et }\cdots \textrm{ et } \cdots$

qui ne serait pas absurde pour quiconque conçoit que les écritures $\Bbb{N}$ ou $0,\,1,\,2,\,3,\, \ldots$ renvoient au même objet, mais on sortirait des formules nécessairement finies de $\mathbf{L}^0$.

Pour $q$, la pensée algorithmique, terrain de jeu de $\mathbf{L}^0$ devrait conduire à proposer

$q=(2 \mid F_5) \textrm{ ou } (3 \mid F_5) \textrm{ ou } (5 \mid F_5) \textrm{ ou } \cdots \textrm{ ou } (641 \mid F_5) \textrm{ ou } \cdots \textrm{ ou } (997 \mid F_5)$

On serait bien en peine de proposer quelque chose de similaire pour $r$. Inutile d’insister pour comprendre que le problème réside dans l’intrusion de l’infini. Une solution remontant à Charles Peirce (1839-1914) et Gottlob Frege (1848-1925) est d’introduire quatre nouveaux concepts : celui d’univers du discours et d’individu appartenant à cet univers¹⁸, celui de variable d’individu et de constante d’individu, celui de fonction propositionnelle (prédicat) $x \mapsto P(x)$ à valeurs dans $\mathbb{F}$ (l’ensemble des formules) et enfin, celui de quantification universelle traduisant la conjonction généralisée et sa négation, la quantification existentielle traduisant la disjonction généralisée.

Pour l’exemple $p$, un univers possible est, l’ensemble $\Bbb{N}$, une bonne variable peut être dénotée $n$, et «$n$ se termine par $5$ (respectivement 25)» peut se traduire à l’aide du prédicat «$n=10\,u+5$» (respectivement «$n= 100 v+25$»)¹⁹. La possibilité d’une telle traduction renvoie clairement à une bonne intelligence de l’écriture décimale des nombres entiers sans même avoir besoin de faire référence à la division euclidienne. Moyennant tout cela, on a une reformulation possible (et improbable) de $u$ :

pour tout entier $n$, si $n=10\,u+5$ alors $n^2 =100\,v+25$

ceci sans préjuger de l’utilité d’une telle formulation pour démontrer, disons au cycle 4, le petit théorème que constitue l’affirmation de $p$.

Quelques multiplications à la main pour voir ce qui se passe durant le calcul peuvent conduire à regarder au bon endroit : le chiffre des dizaines et sa parité : il n’y a alors que deux exemples génériques $15^2$ et $25^2$. C’est un saut conceptuel de traduire «se terminer par 5» par une écriture générique comme $y\,x\,5$ — belle traduction du «tout» — écriture qui se révèle productive : il suffit de poser la multiplication comme on apprend à le faire au CM1 en écrivant soigneusement la retenue dans la deuxième colonne, et de regarder ce qui se passe dans les deux dernières colonnes. Un étudiant a pu être fort étonné de la simplicité du procédé.

Et, signe d’un problème générateur de problèmes, on peut ensuite s’intéresser aux chiffres avant le 25 puis aux chiffres terminaux des cubes, des bi-carrés des nombres terminés par 5 puis au chiffre des unités des carrés en général puis …

L’utilité de cet exemple est d’illustrer la façon dont la quantification universelle permet d’introduire dans les propositions, l’air de rien, l’infini actuel, ce qui est sa fonction essentielle. Dans le cas d’univers fini, a priori $\mathbf{L}^0$ suffit mais cette affirmation n’en valide pas la pertinence.

L’élaboration de la syntaxe d’un²⁰ langage $\mathbf{L}^1$ (morphologie, axiomes, règles de déduction) nécessite un arsenal formel bien plus important — pour ne pas dire indigeste — que celui de $\mathbf{L}^0$ au point qu’on ne le trouve que dans les ouvrages spécialisés. Au niveau universitaire, les rares auteurs qui s’aventurent dans un chapitre 0 sur la logique des prédicats, utilisent directement l’interprétation sémantique de $\mathbf{L}^1$ dans certains contextes des mathématiques (théorie naïve des ensembles, algèbre, arithmétique, analyse) qui servent de support intuitif à la présentation de ce langage [6]. Il n’est alors pas forcément utile d’introduire les sténographies $\forall$ et $\exists$ qui perdent leur raison d’être ; «pour tout» et «il existe au moins un» portent le sens intuitif aussi bien. Notons que, dans les années quatre-vingt, les étudiants raffolaient encore de ces graffitis.

Sans trop insister sur les questions théoriques d’une théorie non faite, les formules $\forall x P(x)$ et $\exists x P(x)$ ne signifient rien en elles-mêmes ; en particulier la seconde n’asserte rien sur une quelconque existence. D’ailleurs le statut de ces «$x$» est fort mystérieux ; N. Bourbaki, fréquemment qualifié de «logicien médiocre» par ses multiples détracteurs, utilise son fameux carré pour l’escamoter et définir les quantificateurs à l’aide du tau de Hilbert (logicien moins médiocre) [7] ; de toutes façons, nos yeux nous trompent : $x$ n’apparaît pas puisque $\forall x P(x) \thickapprox \forall y P(y)$²¹. La question des variables libres ou liées (muettes) est une difficulté majeure déjà en mathématiques pour les étudiants qui sont longtemps perplexes devant l’égalité $\sum\limits_{h=1}^n x_h = \sum\limits_{k=1}^n x_k$ — pardi, il y a des $h$ à gauche et pas à droite — et parfois s’entêtent à vouloir développer $\left(\sum\limits_{h=1}^n x_h\right)^2=\left(\sum\limits_{h=1}^n x_h\right)\left(\sum\limits_{h=1}^n x_h\right)= \cdots$.

Le caractère muet de $x$ dans «$\exists x P(x)$» (qu’on pourrait aussi bien formuler en français) pose parfois un problème redoutable : $x$ n’est pas le nom d’un objet particulier satisfaisant le prédicat $P$.

Dans $\mathbf{L}^1$, il y a une règle de déduction, dite d’instanciation existentielle, pour gérer ce problème : si $\exists x P(x)$ alors $F(a)$ (où $a$ est une constante n’apparaissant pas dans $P$). Ceci ne correspond pas à l’usage en mathématiques ; quand on écrit : «si $r$ est rationnel, alors (par définition) il existe $(a,\,b) \in \ldots$ tel que $r=\dfrac{a}{b}$», dans la suite $a$ et $b$ sont bien considérés comme des noms utilisables ; on ne prend jamais la peine (avec raison !) d’écrire : «soit $(c,\,d)$ un tel couple» (fourni par la règle précédente).

Au tournant du siècle, un étudiant rédigea de façon étonnante une récurrence. D’abord $P(0)$ ; puis supposant qu’il existe $n$ vérifiant $P(n)$, il démontre $P(n+1)$ et conclut : $0$ existe, donc $1$ existe, donc …. L’explication de gravure qui s’ensuivit n’a pas permis de faire fléchir la certitude de cet étudiant²². Il se trouve que cette variante de démonstration par récurrence figurait dans un manuel de Terminale. Qui peut croire qu’exhiber $\left[P(0) \wedge \left(\forall n \in \Bbb{N} (P(n) \Rightarrow P(n+1)\right)\right] \Rightarrow \forall n \in \Bbb{N}\ P(n)$ est une réponse raisonnable à ce genre de problème ? Ne serait-ce pas une incitation à écrire : «supposons que, pour tout $n \in \Bbb{N}$, $P(n)$» ? Certes, il y a des séparateurs qui indiquent la portée du $\forall$. Ah bon, c’est important ?

Les définitions et propriétés des quantificateurs qui peuvent être produites ne sont que des paraphrases du sens intuitif dans le langage courant (le métalangage d’un langage qui reste absent) des expressions «pour tout» et «il existe au moins un» : ainsi «‘pour tout $x, P(x)$’ est vrai» est à comprendre comme «pour chaque $x, P(x)$ est vrai», pardi. Notons que, si l’écriture «pour tout $x \in E$» ($\forall x \in E$) est usuelle en mathématique, elle ne fait pas partie du langage $\mathbf{L}^1$ ; seul y figure $\forall\ x\ P(x)$ ; l’univers du discours reste implicite aux quantifications ! Le plus souvent, cette écriture est introduite sans commentaire particulier ; parfois, il est précisé que pour tout «$x \in E, P(x)$» est synonyme de «pour tout $x$, $( x \in E \Rightarrow P(x))$».

Et, sans ironie dans le propos, la synonymie de «‘il existe $x$ tel que $P(x)$’ est vrai» et de «il n’est pas vrai que, ‘pour chaque $x$, $P(x)$ soit faux’» se comprend par méditation sur le sens des phrases : contemplation et méditation sont d’ailleurs les deux méthodes d’accès aux propriétés des quantifications. Sur de nombreux exemples mathématiques, c’est d’ailleurs préférable.

Pour le dire simplement, la question est un peu indémêlable. La solution, adoptée pour le lycée dans les années quatre-vingt sous l’impulsion d’une inspection générale lucide, de se passer de toute référence explicite à la logique formelle était sans doute pleine de sagesse.

La nécessité de l’objet quelconque

Une des règles de déduction essentielle du calcul des prédicats est celle dite de la généralisation universelle que tout un chacun utilise spontanément sans le savoir :

Soit à démontrer que, pour tout $x \in \Bbb R^{\ast +}$, $x+\dfrac{1}{x} \geqslant 2$. Une production typique de lycéen ressemblera sans doute à : $x+\dfrac{1}{x}-2=\dfrac{x^2-2\,x+1}{x}=\dfrac{(x-1)^2}{x}\geqslant 0$ appuyé par un éventuel « car $x>0$ ». Ce à quoi l’enseignant pourra conseiller d’en améliorer la rédaction en commençant par un « soit $x>0$ » dont la nécessité continuera longtemps de nourrir la perplexité de notre lycéen.

Bien sûr, un lycéen malin de Seconde reconnaîtrait immédiatement dans $\dfrac{1}{2}\left(x+x^{-1}\right)$ la moyenne arithmétique de deux nombres dont le produit — donc la moyenne géométrique, est $1$, ce qui tuerait le problème.

Il faut bien avouer qu’énoncée sous la forme «$\textrm{ si } P(x) \textrm{ alors } \forall x\ P(x)$» , cette règle de déduction a de quoi troubler. Lorsqu’en tête de démonstration, on pose sur le papier «soit $x \in E$» en précisant au besoin «fixé», voire «arbitraire, mais fixé», quel est le statut de cette lettre et que dénote-t-elle ? Serait-ce une variable, mais qui serait constante durant la démonstration ? Serait-ce un paramètre de la démonstration ? Serait-ce le nom d’un objet choisi (secrètement par un bon génie) en début de démonstration mais dont la valeur reste non révélée ? Une constante indéterminée en quelque sorte ? Serait-ce une vraie indéterminée telle le $X$ des polynômes formels ? Mais c’est quoi une indéterminée ?

La géométrie apporte une réponse très spécifique et très pertinente : le «$x$» est le dessin, toujours particulier mais générique, ne contenant pas plus d’informations que n’en fournit l’énoncé ; c’est le fameux «triangle quelconque» de tonton lulu [8] dont la réussite est bien problématique. Peut-on envisager pour notre problème qu’un $x$ particulier soit choisi (par exemple $\pi$ !) et qu’on produise une démonstration qui s’avère valide en remplaçant $\pi$ par $\sqrt{2,7}$ ou par $0,173$ ? Il fut un temps où une démonstration pouvait s’incarner pleinement dans le traitement d’un cas particulier suffisamment générique ; par exemple, le théorème de Thalès démontré dans le cas d’un rapport rationnel particulier, par exemple $\dfrac{2}{7}$. Ne donne-t-on pas ainsi plus de sens à cette généralisation universelle ?

Pour revenir à la question posée, il n’y a probablement pas de réponse unique ; tout dépend du traitement du problème.

Dans la ligne de calcul de la démonstration fournie ci-dessus, $x$ est une indéterminée.

Introduisant un paramètre $y$ et changeant de point de vue, on peut étudier l’équation $\left(x+\dfrac{1}{x}=y\right) \wedge (x>0)$ ; $x$ est donc devenue une inconnue ; reste à obtenir que l’équation a des solutions si et seulement si $y \geqslant 2$ et à interpréter ce résultat.

On peut penser à introduire la fonction $x \longmapsto x+\dfrac{1}{x}$ et en étudier, avec les outils disponibles, les variations ou simplement la voir comme somme de deux fonctions usuelles obtenant ainsi une preuve visuelle très convaincante.

Un étudiant ayant fraîchement étudié les fonctions trigonométriques hyperboliques pourrait poser $x=\exp(t)$ (avec $t=\ln(x)$) et $x+\dfrac{1}{x}=2\,\cosh(t)=2\,\cosh(\ln(x))$ ; waouh !

Dans un oral de concours de grande école recrutant à bac+1, un étudiant a réécrit $x+\dfrac{1}{x}-2=\displaystyle\int_1^x \left(1-\dfrac{1}{t^2}\right)\,\mathrm{d}{t}$ traitant $x$ comme un paramètre, ayant sans doute bien enregistré le fait qu’il y a deux sens de lecture dans toute égalité : $\displaystyle\int_a^b f'(t) \mathrm{d}{t}=f(b)-f(a)$.

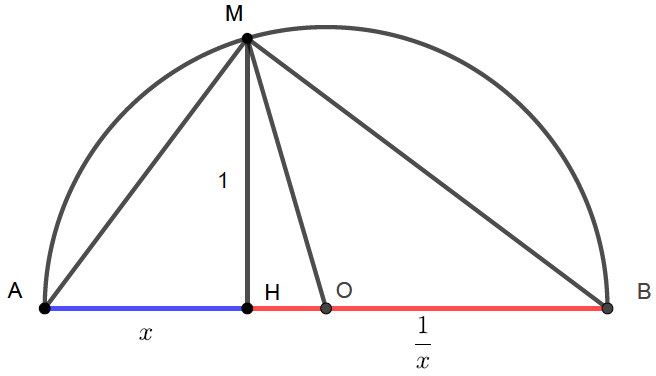
Une preuve visuelle classique avec, à la clé, une propriété métrique du triangle rectangle et le théorème de la projection orthogonale. Le point $\mathsf{H}$ est particulier sur le dessin mais générique, donc $x$ aussi. En géométrie dynamique, on peut saisir le point $\mathsf{H}$ et en faire une variable ; on pourrait d’ailleurs faire représenter graphiquement la fonction $x \longmapsto \mathsf{AB}$.

Pour conclure, choisissons de dire que notre $x$ est le nom d’un objet quelconque de l’ensemble de référence, la métaphore du bon génie aidant à concevoir un tel choix. Cet usage du syntagme soit « $x$ … » est précieux à cultiver y compris dans la formulation des théorèmes en lieu et place des lourds « quel que soit » :

soit $a \leqslant b$, soit $f$ continue sur $[a\,;\,b]$ ; si $f \geqslant 0$ alors $\displaystyle\int_a^b f \geqslant 0$

Bien entendu, la logique des prédicats ne répond pas à une question qui ne trouble guère le mathématicien peu soucieux des problèmes d’engagement ontologique. Mais les débats sur la notion de variable sont plutôt animés dans les milieux philosophiques. Il est d’ailleurs amusant de constater que, pour « justifier » cette règle de la généralisation universelle, les logiciens font référence aux pratiques des mathématiciens. Décidément, qui éclaire qui ?

Venons-en alors à la question des quantifications universelles non explicites : «un carré est à la fois rectangle et losange», «dans un triangle rectangle, le carré de l’hypoténuse est égal …», «l’intégrale d’une fonction positive est positive», «une suite de réels croissante et majorée est convergente», «le déterminant de deux vecteurs est nul si et seulement si ces deux vecteurs sont colinéaires», voire «$(a-b)^2=a^2-2\,a\,b+b^2$». De tels énoncés, qui sont les marques du discours démonstratif, sont sans cesse prononcés dans la classe de mathématiques, écrites au tableau voire dans les copies, s’impriment dans les esprits (certains) et sont réutilisés, certes avec diverses transformations dont nos élèves ont le secret. Admettons la nécessité de l’explicitation des quantifications universelles en particulier dans les énoncés hypothétiques (programme d’e.d.s. de Première) ; mais est-ce vraiment praticable ? On obtient des énoncés le plus souvent indigestes :

$\bullet$ quel que soit le quadrilatère $\mathsf{ABCD}$, $\mathsf{ABCD}$ est un carré si et seulement si $\mathsf{ABCD}$ est un losange et $\mathsf{ABCD}$ est un rectangle ;

$\bullet$ pour tout intervalle $[a\,;\,b]$ (implicitement $a \leqslant b$), pour toute fonction $f$ continue sur $[a\,;\,b]$, si pour tout $x \in I$, $f(x) \geqslant 0$, alors $\displaystyle\int_a^b f(x)\,\mathrm{d}{x} \geqslant 0$.

La pensée à l’œuvre dans la résolution de problèmes s’appuie-t-elle sur de tels énoncés ? A-t-elle besoin de le faire ? Les mathématiques sont un langage mais utilisant des modes d’expression et des registres divers. Un carré est (aussi) un losange, tous les carrés sont (aussi) des losanges, si $\mathsf{ABCD}$ est un carré alors $\mathsf{ABCD}$ est nécessairement un losange, être losange est nécessaire pour être carré, l’ensemble des carrés est inclus dans celui des losanges, et pourquoi pas sous la plume d’un élève : carré $\Rightarrow$ losange (à condition que l’orientation du carré soit bonne). Toutes ces façons de s’exprimer sont dignes d’intérêt ; la simplicité est gage de mémorisation, d’agilité de la pensée quitte à se fourvoyer. La pratique se chargera de corriger et de préciser ce qui doit l’être. Et ceci est certainement d’autant plus pertinent que les mathématiques se compliquent.

Les quantifications multiples

Effectivement la plupart des définitions et théorèmes, formulés selon les règles de l’art, sont des énoncés multiplement quantifiés. Un bon exemple est celui des fonctions affines.

Une définition fréquente dans les manuels ressemble à quelque chose comme :

une fonction $f$ est dite affine si (et seulement si) elle est de la forme $f(x)=a\,x+b$ où $a$ et $b$ sont deux réels donnés (ou fixés, ou constants, ou indépendants de $x$).

On pourrait commenter à l’infini les imperfections d’une telle définition. Sans doute faudrait-il prendre la peine d’écrire à un moment ou un autre :

« il existe deux réels $a$ et $b$ tels que, pour tout réel $x$, $f(x)=a\,x+b$ »

avec l’argument didactique que les implicites sur les quantifications nuisent à la bonne compréhension du concept visé. Pour un lycéen, une fonction affine n’est-ce pas essentiellement « $a\,x+b$ ». Parfait, cela dit l’important. Chaque enseignant a sans doute son idée sur l’empan (mémoire) des élèves de Seconde et sur leur compréhension du concept de fonction et ce qu’elle autorise en matière de définition. Le point clé n’est-il pas l’idée de forme ? Forme de l’expression de la fonction, liée à la forme de la représentation graphique ? Forme identifiable à l’aide de deux paramètres ? Forme associée à certaines propriétés particulières : deux images connues, fonction connue ! Curieusement, l’unicité d’écriture, si précieuse, n’est jamais évoquée sans doute parce qu’on ne travaille que sur des exemples.

La question est toujours au bout du compte de confronter le souhaitable au possible. Or il est justement bien possible que les diverses garnitures quantifiantes des définitions et théorèmes ne soient pas vraiment lues, au mieux parcourues des yeux, dans l’attente de ce qui va vraiment dire quelque chose au lecteur lycéen.

La définition de «suite majorée» est un paradigme : $\exists \ldots\ \forall \ldots$ ; double quantification hétérogène !

Quoiqu’on fasse, il y a toujours une partie (décroissante certes) des élèves qui reste verrouillée sur l’idée que démontrer qu’une suite $(u_n)$ est majorée, c’est écrire une inégalité $u_n \leqslant \ldots$ ; il est probable que les situations où il est par ailleurs utile d’écrire une majoration $u_n \leqslant v_n$ interfèrent de façon évidente. Typiquement $(1+1/n)^n \leqslant 2^n$ donc … Si on regarde comment fonctionnent ceux qui «ont compris», il appert de leurs productions (ou de leurs échanges en TD) qu’ils utilisent une version effective (pour ne pas dire algorithmique) de la définition : obtenir $u_n \leqslant \ldots$, avec $\ldots$ indépendant de $n$, point sans cesse répété par l’enseignant qui finit par porter. Point de gestion d’un ordre de $\exists$ ou de $\forall$ dans leur pensée : seulement une définition en acte dont la formalisation bien comprise viendra plus tard.

Prenons un autre exemple qu’on pourrait penser relever du niveau Terminale :

Nier la convergence d’une suite à partir de sa définition est d’une extrême complexité qui est bien perceptible dans une traduction formelle de cette définition :

$\exists \ldots$ $\forall \ldots$ $\exists \ldots$ $\forall \ldots$ $(\ldots \Rightarrow \ldots)$

Quadruple quantification hétérogène d’une implication ! Effectivement à la portée d’un élève de Terminale. Un étudiant féru de graffitis pourrait écrire mécaniquement la négation sans forcément comprendre ce qu’il écrit voire en oubliant de nier les prédicats ; expérimenté, il pourrait utiliser cette négation pour démontrer que la suite $((-1)^n)$ est divergente. Mais même très expérimenté, cette négation lui serait de peu d’utilité pour étudier la suite $(\sin(n))$.

Une lycéenne, plus attachée aux aspects intuitifs des mathématiques, a pu naguère argumenter que, pour la suite $((-1)^n)$, il n’y avait que deux candidats limites de même poids ; or il ne peut y en avoir qu’un ! Avec un peu d’aide, une rédaction de divergence n’utilisant que la définition a pu être obtenue. Était-ce utile ? Oui, car les conditions nécessaires de convergence arrivées ensuite furent d’autant plus appréciées.

En un autre lieu, un hypotaupin, lui aussi plutôt intuitif et allergique aux belles rédactions promues dans ce milieu, eut l’idée pour étudier $(\sin(n))$ de remonter au cercle trigonométrique et, ayant partagé le cercle en quatre arcs, chacune donc de longueur $\dfrac{\pi}{2} > 1$, put argumenter : «quand on enroule les entiers sur le cercle, à chaque tour il y a (au moins) un entier dans chaque arc ; en passant au sinus, on en a au moins un dans $[\sqrt{2}/2,1]$ et un dans $[-\sqrt{2}/2,\,-1]$ (sic) donc ‘ça’ diverge». Que demander de plus en matière d’utilisation pertinente de quantificateur et de rédaction d’ailleurs ? Applaudissons.

Ces anecdotes ne servent qu’à insister sur le fait que c’est plutôt la compréhension intuitive des mathématiques disons élémentaires (au sens du XX^e siècle) à l’œuvre dans les problèmes qui est susceptible de donner du sens aux expressions quantifiées plutôt que l’inverse.

En conclusion

En se restreignant à la seule scolarité (collège et lycée), l’intérêt que pourrait avoir une accentuation des aspects logiques des mathématiques, gentiment transposés, n’est guère flagrante. Les programmes de lycée fournissent un catalogue lexical, plus que de notions et du rôle qu’elles pourraient jouer, qui doit bien embarrasser les enseignants.

Dans un manuel, on trouve cette intéressante «définition» : $A$ implique $B$ signifie que si «$A$ est vrai alors $B$ est vrai». Dans un autre, il est écrit que $A \Rightarrow B$ est un lien causal entre deux propositions.

Ces énoncés s’adressent à des élèves ; faut-il, fût-ce au nom de Tarski, s’en offusquer ? Le premier dit ce que l’on fait pour démontrer ou utiliser «$A$ implique $B$». En déduire que si $B$ est faux alors $A$ est faux est naturel. On a les deux premières lignes de la table de vérité. Le second dit qu’il y a quelque chose de mathématique à comprendre dans une implication. Tout est dit.

Les prédicats et leurs quantifications sont certes incontournables mais n’inversons pas les rôles : c’est celui des mathématiques élémentaires bien comprises d’éclairer des concepts logiques difficiles. Restent premiers les objets et les problèmes les mobilisant. Plus tard, l’importance de l’ordre des quantificateurs aidera (un peu) à comprendre la définition d’une suite de Cauchy ; au fait, Cauchy utilisait-il des quantificateurs ? Et expliquer que c’est cela qui lui a fait commettre une célèbre erreur est peut-être un peu facile.

La qualité logique de la parole de l’enseignant et celle des manuels sont sans doute utiles, perfectibles certainement, mais moins essentielles qu’on ne le croit : mieux vaut optimiser la simplicité des énoncés quitte à la payer par de l’implicite ou même de l’ambigu²³. L’expérience permet la rectification par approximations successives sur le temps long.

À l’évidence, une synthèse raisonnable de la logique utile dans la scolarité et de ses interactions avec les mathématiques enseignées à ce niveau reste à élaborer, mais pas sans les enseignants dont les conceptions sont aussi le produit d’une pratique. Vaste chantier.

Références

Belna Jean-Pierre, Histoire de la logique, 2014, Ellipses↩︎
Condamine Marcel, Langage, Logique, Démonstrations, 1996, Editions AGUER Delagrave↩︎
Sandu Gabriel, La quête du sens et de la vérité, in Les chemins de la logique, Dossier Pour la science, 2005↩︎
Hottois, Gilbert, Penser la logique, 1994, De Boeck↩︎
Kleene, Stephen, Logique mathématique, 1987, Editions Jacques Gabay↩︎
Godement, Roger, Analyse mathématique I, 1998, Springer↩︎
Bourbaki, N., Théorie des ensembles, 1970↩︎
Lubczanski, Jacques, Chroniques mathématiques, 1986, CEDIC↩︎

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

François Boucher, à la retraite depuis quelques années, continue de s’intéresser aux mathématiques et à leur enseignement.

Nos collègues intuitionnistes vont sans doute protester.↩︎
En nous excusant par avance auprès du lecteur du tour à venir.↩︎
Maintenir la distinction entre le langage-objet que l’on décrit et le métalangage (le français) utilisé pour le décrire serait utile dans le cas d’un authentique exposé ; la convention d’autonymie — utiliser les mots comme noms d’eux-mêmes, pratique usuelle en mathématiques — va être utilisée, ce qui est presqu’inévitablement source d’embarras.↩︎
Le lecteur, un peu algébriste, comprendra que $\neg$ agit comme une fonction et $\Rightarrow$ comme une opération.↩︎
Les deux autres sont $(\neg B \Rightarrow \neg A) \Rightarrow ( A\Rightarrow B)$ et $(A \Rightarrow (B \Rightarrow C)) \Rightarrow ((A \Rightarrow B) \Rightarrow (A \Rightarrow C))$. On doit ces axiomes à Jan Łukasiewicz (1878-1956)↩︎
Le lecteur aura noté l’emploi du «si …, alors …» ; y-a-t-il diverses façons de comprendre ce conditionnel du métalangage ? Serait-ce un $\Rightarrow$ camouflé ?↩︎
Le lecteur aura noté l’emploi du «si et seulement si» pré-logique ; il n’appartient pas à $\mathbf{L}^0$.↩︎
Le lecteur lira selon sa préférence, «trèfle, cœur» ou «bleu, rouge» .↩︎
Il est utile de voir le coloriage d’une formule comme le prolongement à cette formule d’une application de $\mathbb{A}$ dans $\mathbb{V}$.↩︎
Il n’y a, bien sûr, aucun miracle puisque Łukasiewicz n’a pas choisi ses axiomes au hasard.↩︎
Et, comme souhaité, la réciproque est vraie ; voir ci-après.↩︎
Le lecteur aura noté l’emploi du «tout» ; serait-ce une quantification universelle ?↩︎
Avec un abus d’écriture simplificateur osé mais que nous espérons limpide pour le lecteur !↩︎
D’où les apostrophes utilisées pour distinguer ‘0’ (un zéro formel) et $0$ (un authentique neutre, par exemple celui de $\mathbb{Z}/2\mathbb{Z}$).↩︎
Ceux connus de tous : $0,\,1,\,2,\,3, \ldots$ énumération non limitée.↩︎
Contextes scolaires introduits dans la version papier de la petite enquête.↩︎
La valeur de vérité de $p \intercal q$ ne dépend que de celles de $p$ et de $q$, position qui semble naturelle à un mathématicien ne l’est pas dans toutes les logiques.↩︎
Il ne s’agit pas a priori d’ensemble et d’appartenance au sens usuel ; l’article fondateur de la théorie des ensembles de Georg Cantor date de 1874. Toutefois dans le cadre de la scolarité, il est bien naturel de s’y restreindre↩︎
En temps voulu, la nature de u et v sera précisée ; imagine-t-on qu’écrire : «il existe $u \in \Bbb{N}$ tel que $n = 10 u + 5$» serait plus intelligible côté élève ?↩︎
Il n’y a pas qu’un seul langage du premier ordre.↩︎
$\thickapprox$ désigne l’identité dans $\mathbf{L}^1$ ; on suppose que $y$ n’apparaît pas dans $P(x)$.↩︎
Mais il acceptera de modifier sa pratique pour les concours.↩︎
Que les collègues membres des jurys de concours ne s’étranglent pas d’indignation.↩︎

Pour citer cet article : Boucher F., « Petite enquête sur … la logique dans la scolarité – Complément numérique », in APMEP Au fil des maths. N° 544. 6 novembre 2022, https://afdm.apmep.fr/rubriques/ouvertures/petite-enquete-sur-la-logique-dans-la-scolarite/.

Au fil des maths