Activités Streetmath
Sortez vos craies et vos envies de partager la beauté des maths ! C’est parti pour de multiples projets de fresques collectives ! Cet article est publié en parallèle dans le numéro hors-série «spécial diffusion» de la Gazette de la Société Mathématique de France  .
.
Marie Lhuissier & Olga Paris-Romaskevich pour l’association Mathématiques vagabondes, Nathalie Corson & Alice Ernoult
© APMEP Juin 2023
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Notre association, créée en mai 2020, fait vivre l’art et la science à travers des expériences partagées, avec une attention particulière portée aux mathématiques. L’idée de notre projet Streetmath : faire vivre les images mathématiques dans l’espace public. Nous voudrions la partager avec la communauté, pour emmener Streetmath partout où souffle le vent. Pour le moment, nous faisons les dessins éphémères à la craie.
Lors des séances de Streetmath, certains objets et images sont découverts pour la première fois par le public (comme la fractale de Sierpiński ou les nœuds) ; certains autres (droites tangentes, cercles, symétrie axiale…) sont déjà familiers mais gagnent en couleur dans l’imaginaire des participants !
Où et quand ?
Sur les places de Lyon, un dimanche par mois.
Quel matériel ?
Grosses craies de trottoir (compter 5 à 7 craies par personne et par heure), plusieurs cordelettes de taille adaptée d’une dizaine de mètres (pour certains motifs), un peu d’eau et des éponges pour effacer (en cas d’erreur).
Matériel spécifique : voir les activités.
Avec qui ?
Tous les volontaires ! Nous lançons l’appel sur nos réseaux. Cela nous amène un public très varié, en âge et en culture mathématique. Les passants se joignent à nous pour participer en cours de route. Activité adaptée aux familles avec des enfants à partir de six ans.
Quelles précautions à prendre ?
S’assurer que le lieu correspond à l’activité proposée (pas trop de passage, place suffisante, dallage adapté au motif, qualité du sol — un sol granuleux demande beaucoup de craie !) et que le temps est bon (éviter Streetmath sur le sol mouillé !).
Nos critères pour le choix des motifs
Il s’agit d’assurer une œuvre collective, esthétique et mathématiquement intéressante en partant d’instructions simples. Nous décrivons ici quatre de nos activités notées sur la grille ci-dessous, selon les critères suivants :
-
les instructions sont-elles claires et simples ?
-
la mise en place est-elle facile ?
-
le dessin a-t-il plusieurs parties indépendantes ?
- le résultat est-il mathématiquement intéressant ?
Chaque critère est noté entre 1 et 3 points, 3 étant la note la plus haute.
| Activité | instructions | mise en place | indépendance | maths |
| Sierpiński | 3 | 3 | 3 | 3 |
| Mandalas | 3 | 2 | 2 | 1 |
| Nœuds | 1 | 2 | 2 | 3 |
| Courbe | 3 | 1 | 2 | 2 |
| Vasarely | 3 | 2 | 3 | 2 |
Contact
Pour vos idées d’activités Streetmath ou plus d’informations :
Vous voulez proposer une activité Streetmath à votre classe, musée, centre social, famille ? Vous pouvez le faire en toute autonomie avec nos fiches, ou faire appel à nous et on s’occupe de tout ! Nous proposons également des cartes postales avec les photographies des œuvres Streetmath créées à Lyon, à commander sur le site de l’association ou lors de nos événements.
| Voici plusieurs activités Streetmath. |
Le triangle de Sierpiński (fractale)
Lieu
Grande place avec des pavés en quinconce.
Figure 1. Triangle de Sierpinski à 128 lignes, fait par douze personnes (dont cinq enfants) en 2 heures.
Photo : Bertrand Paris-Romaskevich
Principe mathématique
Le triangle de Sierpiński est une fractale dont la forme globale est celle d’un triangle équilatéral, subdivisé de façon récursive en triangles équilatéraux plus petits. Il existe de nombreuses manières de construire cette fractale ; l’une d’elles est par automate cellulaire : dans une grille infinie, à chaque étape de nouvelles cases sont coloriées, en fonction de l’état (colorié ou non) de leurs voisines. Pour plus d’informations concernant cette construction, vous pouvez consulter l’article de Tangente Magazine .
L’intérêt de ce motif est son autosimilarité : il est composé de trois copies plus petites de lui-même. En conséquence, on peut séparer le grand motif en trois parties indépendantes sur lesquelles travaillent simultanément trois groupes.
Mise en place
Trouvez une place dont les pavés sont disposés en quinconce. Déterminez en amont la taille désirée (\(2^n\) lignes). Coloriez le premier pavé, puis tracez des croix sur les \(2^{n-1}-1\) pavés qui partent obliquement de part et d’autre du premier pavé. Au \((2^{n-1})\)-ième pavé, coloriez à nouveau. Les trois pavés coloriés sont les sommets des trois triangles de Sierpiński qui formeront le grand.
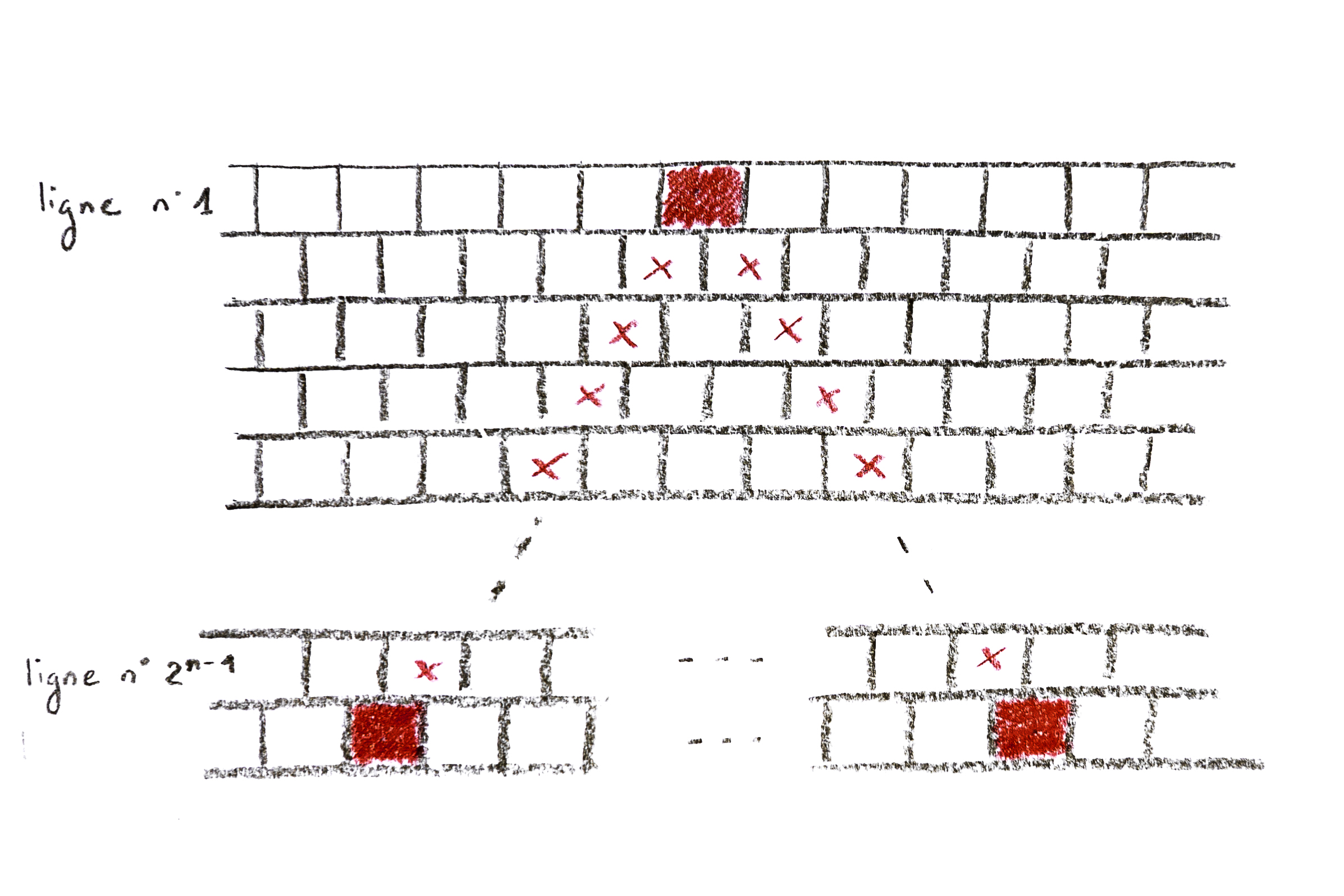 Figure 2. Mise en place du triangle de Sierpinski
Figure 2. Mise en place du triangle de Sierpinski
Déroulement
Formez trois groupes qui travailleront sur les trois triangles. Appliquez les instructions suivantes à chacun des trois triangles : le pavé colorié vaut \(1\), les autres (vides) \(0\). Sur la ligne en-dessous, chaque pavé sera la somme des deux au-dessus de lui, avec une particularité : \(1+1=0\) ! Coloriez les pavés qui valent \(1\). Descendez ainsi ligne par ligne, en vérifiant régulièrement (symétrie, régularité du motif). Vous verrez émerger une fractale de Sierpiński.
Conseils
Tracez des croix avant de colorier (les erreurs se propagent vite !) car une croix est plus facile à effacer qu’un pavé colorié. Prévoyez une personne qui vérifie qu’il n’y a pas d’erreur et qui donne le feu vert pour le coloriage.
Deux éléments faciles à vérifier pour repérer d’éventuelles erreurs : dans chaque motif, les lignes de hauteur \(2^k\) doivent être entièrement coloriées et la figure doit avoir un axe de symétrie vertical.
Tresses, nœuds et entrelacs
Lieu
Place vierge ou avec de grands pavés (pour les nœuds et entrelacs) ou avec une grande bande (pour les tresses).
Principe mathématique
Tous les nœuds, tresses et entrelacs peuvent être codés par des graphes, ce qui les rend bien plus simples à mémoriser et dessiner ! Pour passer du graphe à l’entrelacs, la méthode est la suivante : on dessine au milieu de chaque arête un croisement de deux brins puis on relie les brins en suivant le graphe, sans le traverser.
 |
 |
Ce processus n’est pas évident et nous manquons de place ici pour l’expliquer correctement. Si vous ne le connaissez pas déjà, nous vous conseillons vivement de lire l’article De beaux entrelacs de Christian Mercat, qui le présente de façon détaillée sur le site Images des Mathématiques du CNRS .
Mise en place
Décidez-vous sur le nœud, l’entrelacs ou la tresse à dessiner. Tracez son graphe au sol.
Déroulement
Expliquez la méthode permettant de dessiner un nœud, une tresse ou un entrelacs à partir d’un graphe : dessiner les croisements, relier les brins, épaissir les brins, ombrer les croisements. Laissez chacun s’entraîner au sol sur de petits graphes. Quand tout le monde est à l’aise avec la méthode, tracez le grand entrelacs à l’aide du graphe préalablement dessiné.
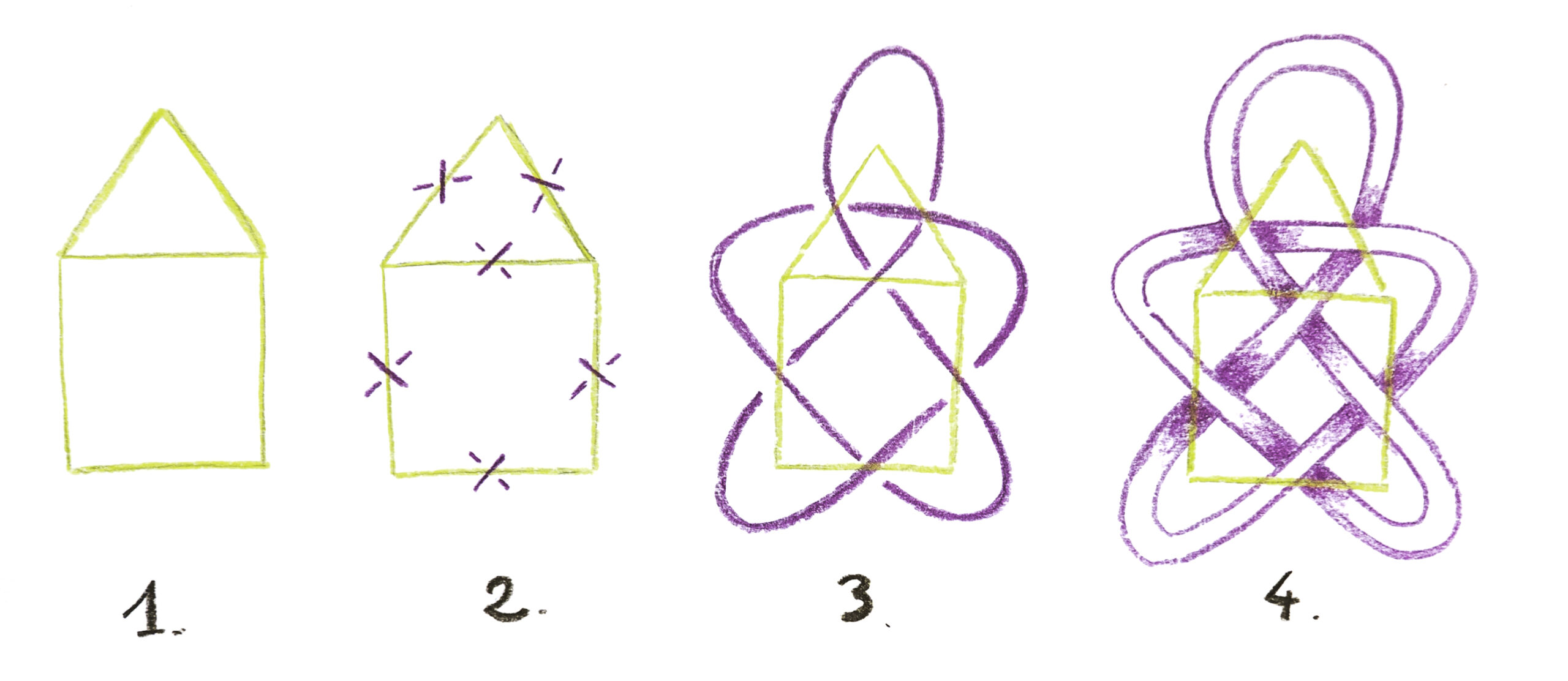
Photo : Bertrand Paris-Romaskevich
Conseils
Vous pouvez choisir une place dont les pavés vont vous aider à tracer le graphe. Distribuez des petits papiers indiquant la convention pour les croisements et/ou dessinez un tutoriel. Il est possible de colorier le complémentaire de la tresse à la fin pour la faire mieux ressortir (attention, beaucoup de craie dépensée à cette étape !).
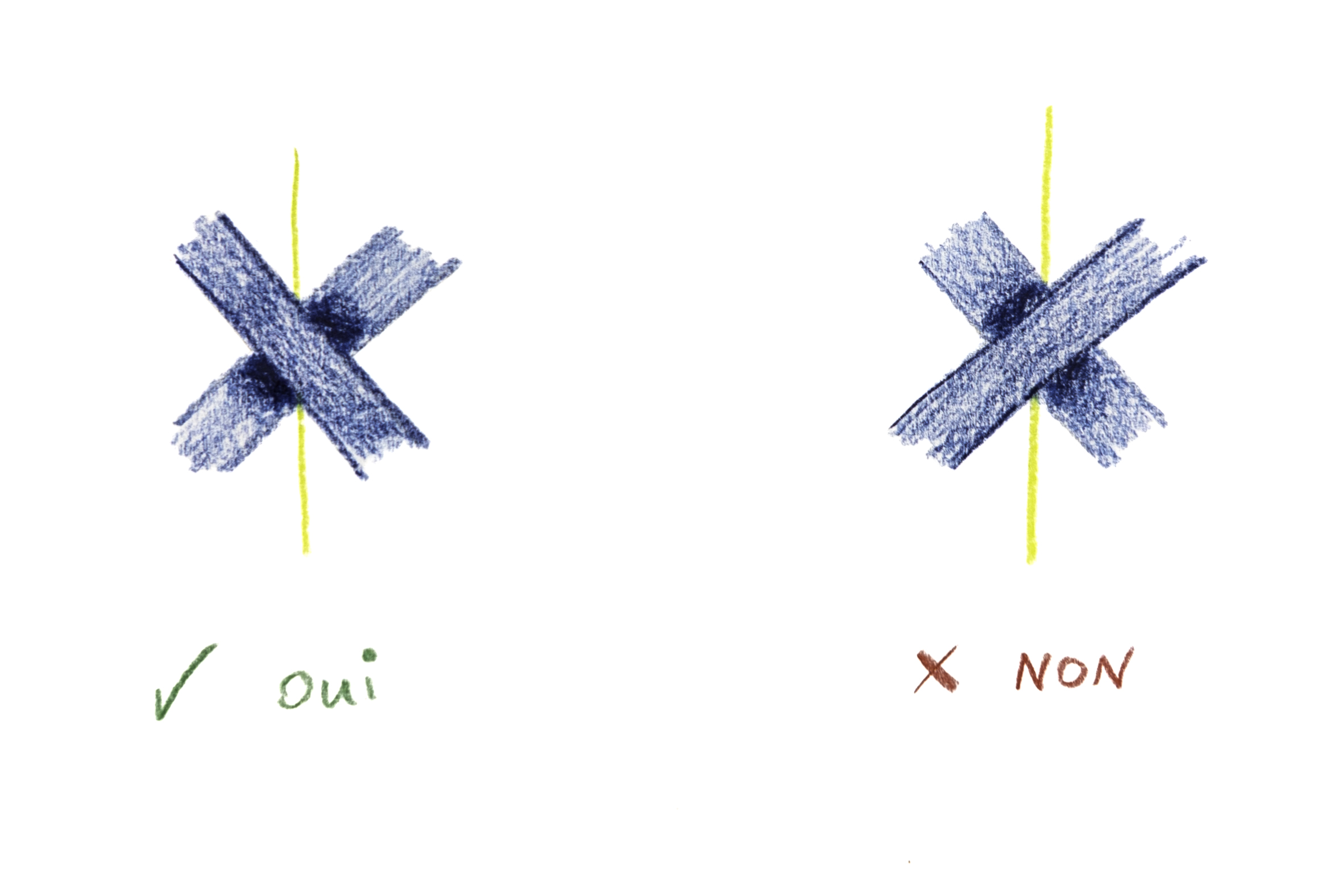
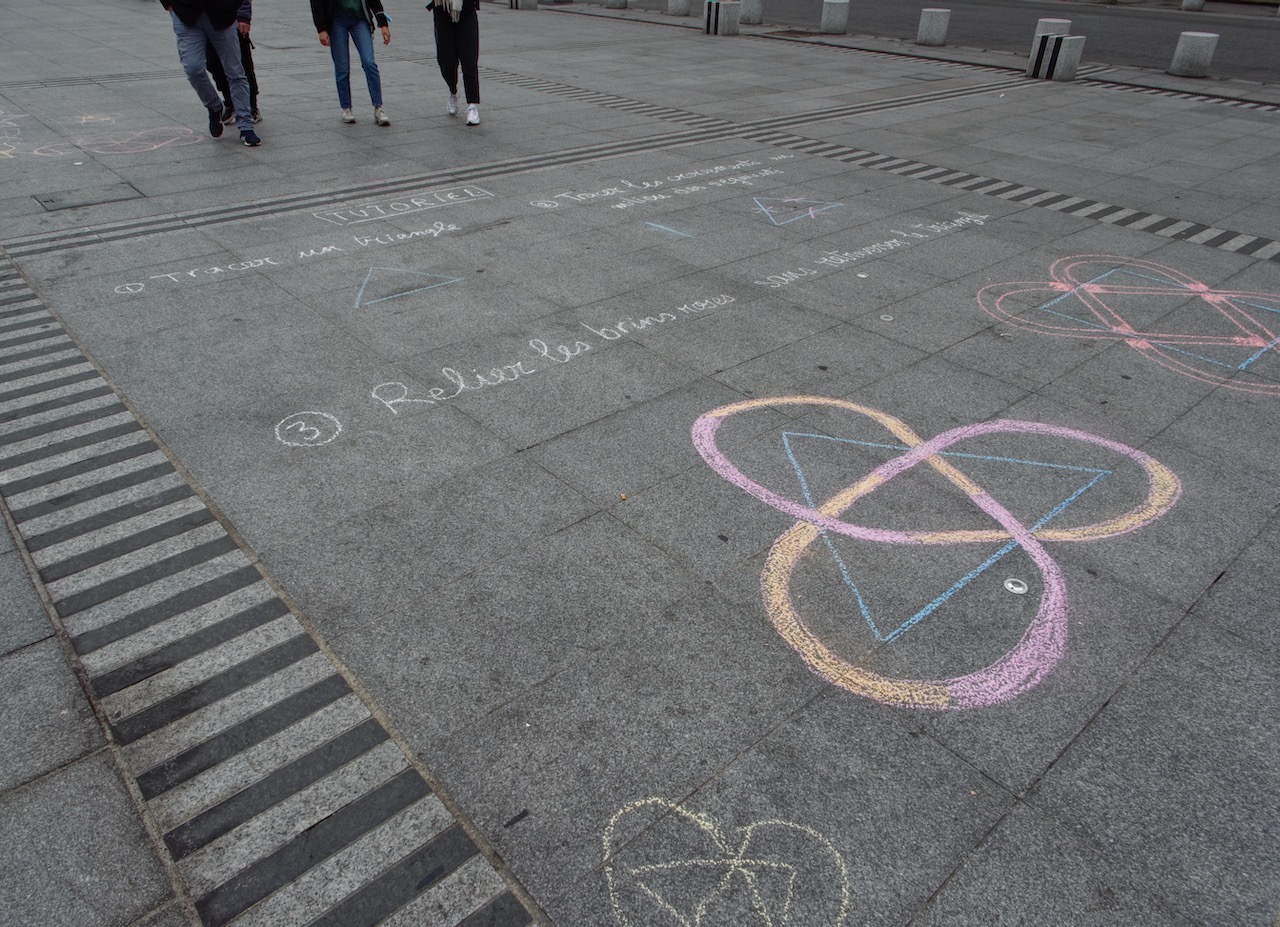
Photo : Bertrand Paris-Romaskevich
Mandalas
Lieu
Place vierge (et encore mieux, ronde !).
Principe mathématique
Il s’agit de créer une grande figure circulaire (mandala signifie cercle en sanskrit) avec beaucoup de symétries : \(8\), \(12\) ou \(16\) axes de symétrie, ou alors des symétries circulaires d’ordre \(8\), \(12\) ou \(16\).
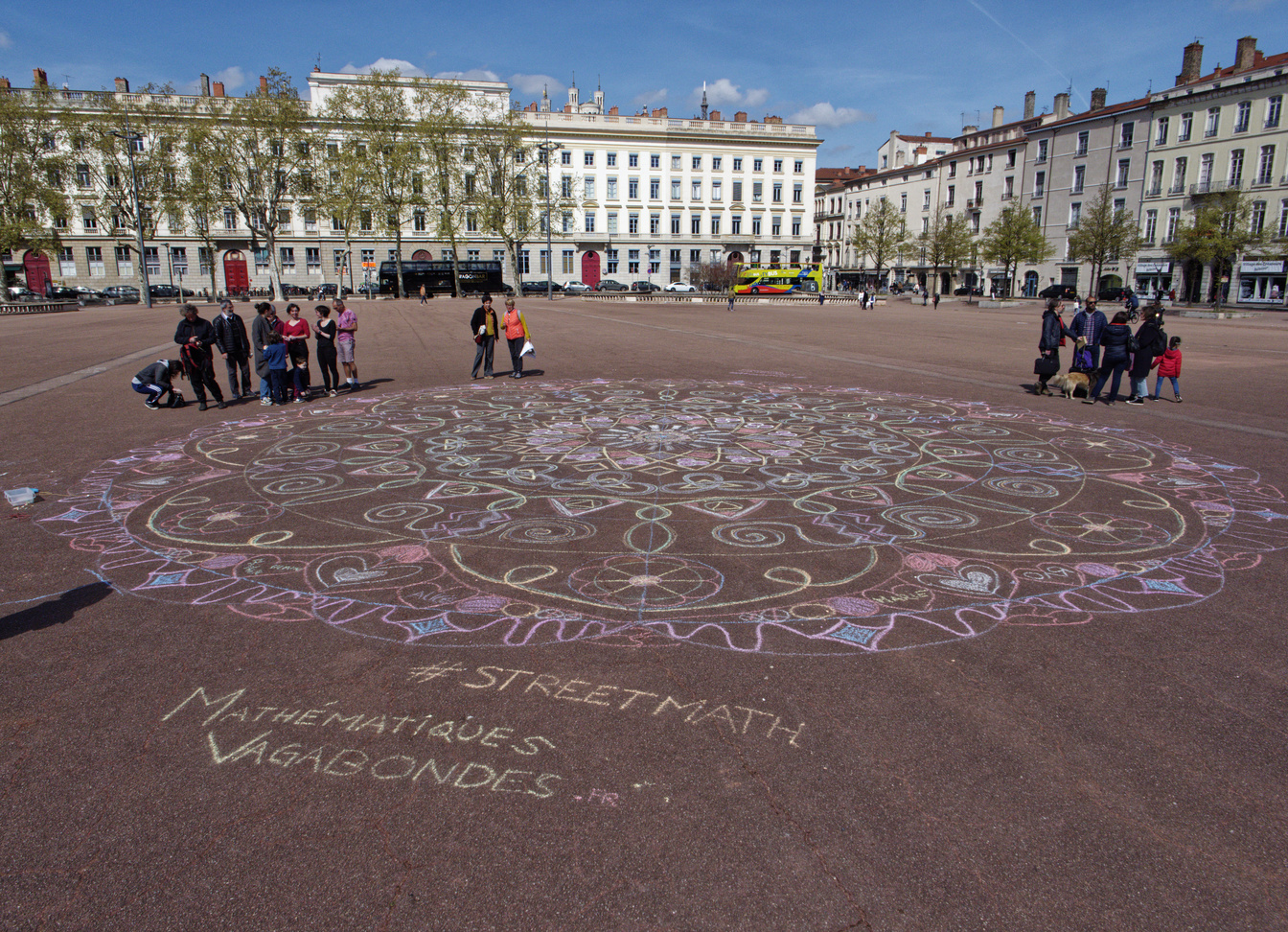
Photo : Bertrand Paris-Romaskevich
C’est une activité qui laisse grande place à la créativité car les motifs à choisir sont libres. Son intérêt est de découvrir la symétrie axiale et de vivre de façon physique l’expérience inoubliable de tracer un grand cercle.
Mise en place
Choisissez le centre du mandala, puis dessinez plusieurs cercles concentriques (environ 8), à espacement variable (ce qui donnera des bandes de taille différentes pour le répétition des motifs). Divisez le grille circulaire en secteurs de taille égale :
-
dessinez d’abord un diamètre (deux personnes qui tiennent des bouts de corde, une qui trace) ;
-
puis divisez les angles en parties égales grâce à l’une des constructions géométriques suivantes :
-
soit en reprenant la construction de la bissectrice au compas avec une cordelette,
-
soit en utilisant une feuille de papier que vous pliez en deux pour subdiviser l’angle en partant du centre.
-
On obtient ainsi huit ou seize secteurs. À l’aide de la construction au compas de l’hexagone régulier, on peut aussi obtenir une grille à six ou douze secteurs.
Déroulement
Une fois que la grille est prête, chacun est libre de dessiner le motif de son choix dans une case de la grille et puis s’occupe de le reporter dans toutes les cases de la bande circulaire. Plusieurs dessins se font ainsi en parallèle. On peut choisir de reporter les motifs par rotation ou par symétrie axiale (c’est moins évident !)
Conseils
Il faut être vigilant à ne pas croiser les motifs pour ne pas créer d’incohérences. Pour cela, réunissez-vous à plusieurs et créez des dessins ensemble, aidez les autres à reporter leur motif dans tous les secteurs, ornez et complexifiez les motifs déjà créés. Le dessin émerge petit à petit et de nouveaux éléments peuvent être ajoutés dans les bandes.
Une courbe rien qu’avec des droites
Lieu
Une place vierge, ou avec des grands pavés, ou autres grandes zones délimitées par des segments.
Principe mathématique
La parabole est une courbe qui a la particularité d’être l’enveloppe de droites obtenues de manière bien particulière : à partir de deux familles de points alignés et régulièrement espacés, qu’on relie successivement deux à deux. Pour plus d’informations sur cette construction géométrique, on pourra consulter la page Wikipedia Enveloppe (géométrie) .

Photo : Bertrand Paris-Romaskevich
Mise en place
Tracez deux segments (perpendiculaires ou pas) qui ont une extrémité commune. Dessinez-les à l’aide d’une cordelette tendue ou en vous appuyant sur la géométrie de votre place (rebords, grilles, bord des dalles, etc.). À l’aide d’une cordelette de taille adaptée, faites des marques régulièrement espacées (dix, vingt, trente marques… autant sur les deux segments). Numérotez-les, en partant de l’extrémité libre pour un des segments et de l’extrémité commune pour l’autre.
Déroulement
Reliez les marques de même numéro. En ne traçant que des lignes droites, vous verrez ainsi apparaître une courbe parfaite, un arc de parabole —comme une pensée un peu fantaisiste qui émerge par magie d’un univers rectiligne !
Conseils
Vous pouvez faire un grand dessin ou plusieurs petits dessins. Cette méthode marche aussi très bien pour décorer les lettres de l’alphabet !

Bonus : pavages d’hexagones par des losanges
Auteures : Nathalie Corson et Alice Ernoult.
Le vent lyonnais a soufflé l’inspiration de Streetmath jusqu’en Normandie où une petite équipe de mathématiciennes s’est emparée de l’idée. En association avec des professeures des écoles, il s’agit de décliner Streetmath avec des classes pour des ateliers en deux temps.
Une première partie est consacrée à la présentation du projet et des mathématiques sous-jacentes, la seconde est une réalisation artistique.
Pour chacune de ces activités, une fiche pratique présentant un déroulement possible de l’activité et le matériel associé est librement consultable.
Des documents ressources pour cette activité sont disponibles sur le site de l’APMEP .
Le matériel est prévu pour être utilisable avec la présence ou non d’une personne chargée de la médiation.
Nous vous présentons ici la première activité de ce type, inspirée des cubes de Victor Vasarely1. D’autres sont en cours d’élaboration.
Lieu
Une salle de classe et la cour de l’école ou du collège.
Matériel
-
puzzle en bois ou en papier ;
-
des cordes avec un nœud pour le doigt et un nœud pour la craie avec une longueur fixée (si on utilise les gabarits) ;
-
un gabarit de losange par groupe d’enfants ;
-
un tasseau ou tout autre objet rigide qui puisse servir de règle pour tracer les segments ;
-
de grosses craies d’au moins trois couleurs.
Principe général
Cette activité menée avec des enfants (à partir de sept ans) permet de découvrir, manipuler et reproduire des pavages d’un hexagone par douze losanges. L’observation de différents pavages et la manipulation du puzzle, avec ou sans coloriages, amènent des discussions autour de la représentation d’objets en trois dimensions. Le puzzle sert également de modèle pour la construction géométrique, en grande taille, à l’extérieur.


Mise en place
Pour la discussion en classe, prévoir des dessins de différents pavages de l’hexagone par douze losanges (avec ou sans coloriage) et les puzzles (en bois ou en papier).
Au moment du tracé dans la cour, pour les élèves les plus jeunes, il est préférable de pré-tracer le cercle et l’hexagone et de privilégier l’utilisation des gabarits.
Déroulement
-
Observation en classe de différents pavages d’un hexagone par douze losanges.
-
Manipulation de ces pavages avec un puzzle en bois ou en papier pour faire le plan du puzzle qui sera réalisé dans la cour.
-
Construction dans la cour : tracer un cercle en utilisant la corde comme un compas, reporter la distance pour découper le cercle en six portions égales, tracer l’hexagone en reliant les points du cercle. Puis choisir l’une des méthodes suivantes :
- \(\star\) avec les gabarits,
-
reproduire les losanges avec le gabarit en commençant par un sommet de l’hexagone en suivant le plan élaboré par une partie de l’équipe ;
- \(\star\) sans les gabarits,
-
partir de l’hexagone, placer le milieu de chaque côté de l’hexagone (en pliant la corde en deux), relier les parallèles aux côtés passant par deux sommets ou deux milieux, tracer au trait plus fort les losanges en reproduisant le plan prévu par la partie de l’équipe travaillant sur le plan.
-
Finition par le coloriage du pavage obtenu.
Conseils
Il faut accepter les imprécisions de tracé qui peuvent être facilement corrigées en grossissant certains traits, en décalant légèrement certaines parties ou au moment du coloriage. Ne pas hésiter à accompagner les enfants pour cela.
Si une personne chargée de la médiation est suffisante pour la partie en classe, l’accompagnement par plusieurs adultes est un plus pour la partie en extérieur. À titre d’exemple, lors de nos interventions, des étudiants de licence et de master de mathématiques sont venus nous prêter main-forte.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Marie Lhuissier est conteuse-mathématicienne
.
Olga Paris-Romaskevich est chercheuse en mathématiques et très active dans la diffusion des mathématiques notamment via les arts.
Elles ont fondé ensemble l’association Mathématiques vagabondes.
Nathalie Corson est enseignante-chercheuse au laboratoire de mathématiques appliquées du Havre (LMAH), université Le Havre Normandie.
Alice Ernoult est professeure de mathématiques au lycée François Ier du Havre et membre de l’APMEP.

Une réflexion sur « Activités Streetmath »
Les commentaires sont fermés.