Le pavé dans la boîte en Sixième

L’activité décrite ci-dessous a été présentée lors du stage PAF « Manipuler pour concevoir en Mathématiques » animé par le groupe MONAF ¹ de l’IREM de Rouen. Elle a pour objectif d’aider les élèves de 6^e à concevoir le pavé droit dans ses différentes représentations et de l’évoquer en utilisant le vocabulaire approprié.

Anne Dusson et Nathalie Lecouturier

© APMEP Juin 2019

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

L’activité est conçue sur plusieurs séances de 55 minutes après les rituels (calcul du jour, questions flash, …). Par expérience, les étapes 1 et 2 peuvent se faire lors d’une même heure de cours. Les étapes 3, 4 et 5 prennent chacune une heure et l’étape 6 commencée à une fin d’heure se poursuit sur une partie de l’heure suivante. On part de l’objet concret puis les différentes manipulations et observations permettent d’arriver aux définitions et caractérisations du pavé droit et de la notion de patron, et de définir les règles de la perspective cavalière.

Préparatifs

Avant la première séance, on demande aux élèves de préparer une boîte en carton parallélépipédique (de médicament, de dentifrice…) de la façon suivante : couper les languettes que l’on ne voit pas quand la boîte est fermée puis refermer la boîte en scotchant les ouvertures.

Étape 1 : des objets connus

On présente aux élèves différents solides de la vie quotidienne puis on leur demande de les nommer (boule, pyramide, cône, cylindre, prisme, cube, pavé droit).

Il est important de montrer les objets en vrai et non des photos qui sollicitent la vision en perspective, vision qui sera travaillée plus tard. On convient ensemble de définir deux catégories : celle des polyèdres (le mot est donné à ce moment-là) et les autres. Puis on introduit le mot de polygone pour désigner chaque face des polyèdres.

Étape 2 : description de la boîte

Il faut parfois préciser oralement que l’on attend le maximum de renseignements mathématiques, qu’importe la marque de dentifrice !

Durant la mise en commun émerge le vocabulaire : face, arête, sommet, rectangle, carré, solide, figure, arêtes parallèles, arêtes perpendiculaires, pavé droit, longueurs des arêtes.

On enrichit le vocabulaire avec les notions suivantes : faces parallèles, faces perpendiculaires, segment, droite, point, longueur d’un segment. On introduit les notations d’un segment, d’une droite ainsi que les trois dimensions du pavé droit. On redéfinit le rectangle et le carré. C’est l’occasion de faire découvrir que le carré fait partie de la famille des rectangles. Un grand moment de déstabilisation et de remise en cause des connaissances pour la plupart !

Dans le cahier, en institutionnalisation, le pavé droit est défini : un pavé droit est un polyèdre formé de six faces, toutes rectangulaires.

Étape 3 : mise à plat

1. Consigne orale : « Découper la boîte suivant les arêtes pour la mettre à plat. La forme obtenue doit être d’un seul morceau ».

   Cette mise à plat permet d’introduire le mot patron qui est parfois proposé par les élèves eux-mêmes.

2. Consigne orale : « Sur le patron, colorier d’une même couleur les faces parallèles et d’une même couleur les arêtes de même longueur ».

   C’est l’occasion d’introduire le codage des segments de même longueur (arêtes) et de l’angle droit.

3. Consigne orale : « Par 2 ou par 4, comparer les différentes formes obtenues ».

   Au bout de dix minutes, on fait une mise en commun de la façon suivante : un élève vient au tableau coller son patron, ceux qui ont un patron de la même forme viennent le coller dans la même colonne. Puis un patron d’une autre forme est collé puis un autre, etc. On établit un classement selon un critère que l’on nomme pour le moment « forme » et qui se construit à l’aide d’exemples « oui » et d’exemples « non » selon la méthode de Britt-Mari Barth².

Les élèves justifient le choix de la famille par la position des faces indépendamment de leur taille. On est amené à distinguer en deux colonnes intitulée : Qu’est-ce qui change ? et Qu’est-ce qui ne change pas ? Si l’on n’obtient pas assez de familles différentes, les élèves reprennent leur boîte, la referment avec du scotch, puis la découpent à nouveau pour obtenir une autre forme. À la fin de ce travail de classement, on garde au tableau, ou sur une affiche qui servira plusieurs séances de suite, un patron de chaque famille trouvée.

On introduit à l’oral la notion de disposition des faces.

Cette activité de comparaison est très formatrice pour les élèves. Elle fait émerger les différences et les similitudes sur des objets à la portée de quasiment tous les élèves de 6^e et elle ouvrira la possibilité de transferts à d’autres activités de comparaison à condition de laisser aux élèves le temps de l’évocation et de la verbalisation du travail effectué.

Dans le cahier, en institutionnalisation : Les formes obtenues s’appellent des patrons. Les patrons ne sont pas tous identiques mais ils sont tous constitués de six rectangles deux à deux identiques. Un pavé droit a plusieurs patrons différents.

Étape 4 : patrons de cube

Les élèves ont des cahiers avec des carreaux Seyès, ce qui facilite les tracés. Les plus rapides sont invités à trouver d’autres patrons de cube. Les plus lents se contentent de deux ou trois patrons. Les plus en difficulté peuvent dessiner leur assemblage de six carrés sur du bristol quadrillé et le découper pour vérification³

Lors de ce travail, si l’on utilise uniquement la reproduction sur le cahier sans avoir recours au découpage pour vérification, on rend obligatoire l’évocation dans la tête de la fermeture (ou pas !) du patron.

Étape 5 : patrons de pavé droit

Matériel : six rectangles ( trois paires de rectangles de couleurs différentes et de dimensions : \(3 cm \times 4,5 cm\),  \(3,5 cm \times 4,5 cm\),  \(3 cm \times 3,5 cm\) ), du scotch et une paire de ciseaux.

Les élèves peuvent s’auto-corriger en refermant (ou pas !) le patron. Voici par exemple des essais d’élèves. Certains assemblages sont éliminés car on n’obtient pas le pavé droit souhaité en refermant.

Les plus rapides peuvent chercher plusieurs solutions avec le même ensemble de rectangles. Sur du papier à petits carreaux, les élèves qui trouvent plusieurs patrons les reproduisent au fur et à mesure. Dans le cahier, les élèves dessinent un patron de pavé droit en utilisant le quadrillage du cahier, ils codent les angles droits, les segments de même longueur puis collent, sur une seule face, le patron constitué des six rectangles de couleur de façon à pouvoir le refermer (il est souvent différent de celui construit).

Étape 6 : représentation en perspective cavalière

Matériel : une feuille blanche de format A6 pour chaque élève.

Un pavé droit, type boîte à chaussures, est posé sur le bureau (boîte assez grande pour être visible de tous les élèves).

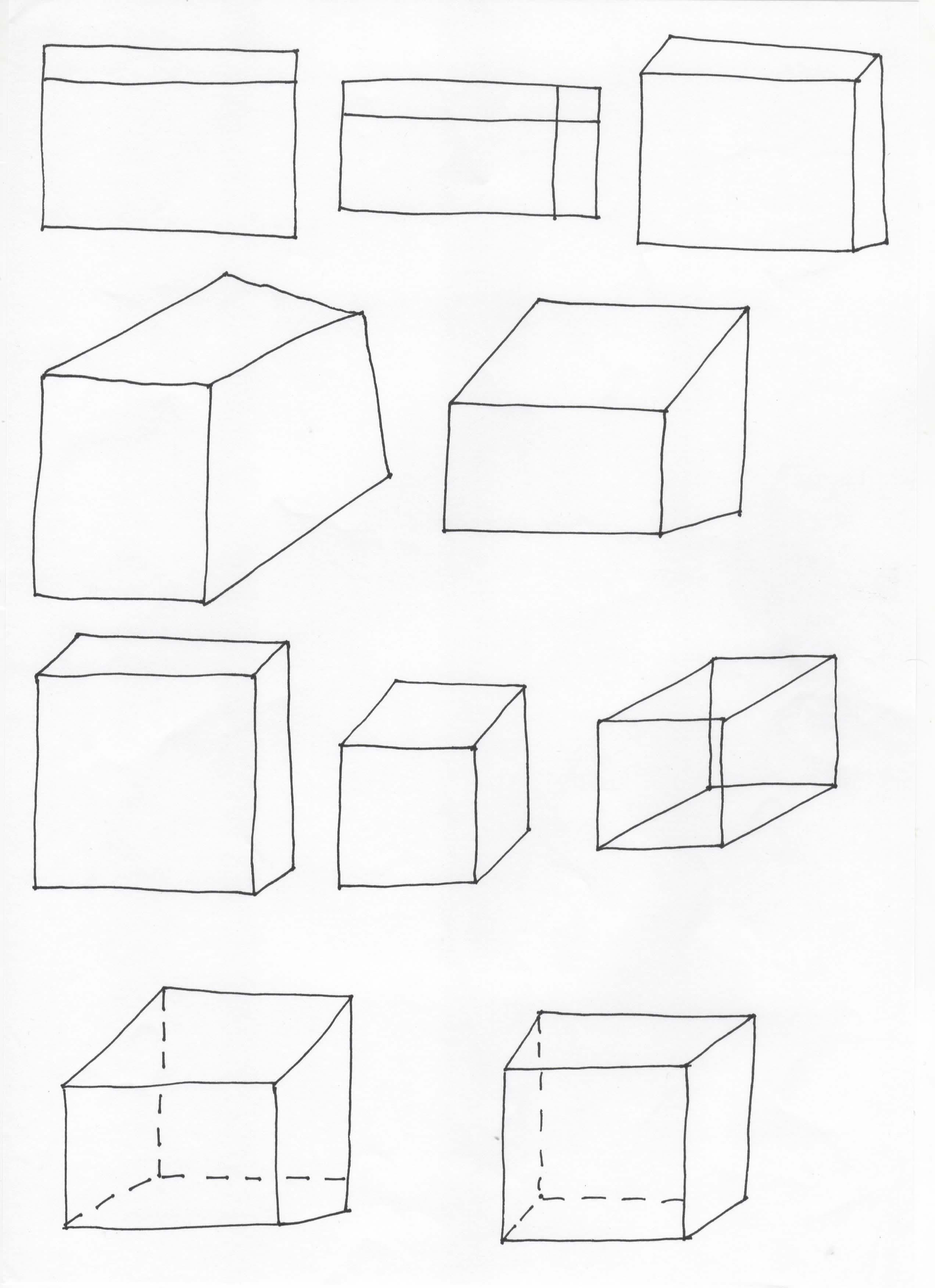
Ce travail qui prend à peine dix minutes peut être réalisé à la fin d’un cours, en dehors de toutes les étapes précédentes. On ramasse les feuilles et on part du travail des élèves pour élaborer les règles de perspective. Une feuille blanche permet à l’élève de transcrire son image mentale sans se conformer à un cadre qui serait donné par un quadrillage. Le dessin se fait à main levée et oblige l’élève à faire des allers-retours entre sa perception et son évocation.

Mise en commun et débat de classe

Les réponses des élèves sont triées puis montrées à la classe l’une après l’autre pour arriver à concevoir et verbaliser les règles de perspective, toujours grâce à des exemples « oui » et des exemples « non ». Il est important d’introduire auprès des élèves la notion de « critique bienveillante » en précisant qu’on ne cherchera pas à savoir qui a fait telle ou telle figure et en rectifiant toute remarque désobligeante. Le débat de classe doit se faire dans un climat de confiance.

Dans le cahier, en institutionnalisation, les élèves écrivent les règles de représentation en perspective et dessinent un pavé droit en perspective.

• Les faces avant et arrière sont dessinées en vraie grandeur.

• Les arêtes parallèles dans la réalité sont représentées par des segments de directions parallèles sur le dessin en perspective.

• Les dimensions des arêtes fuyantes sont réduites par rapport aux dimensions réelles.

• Les arêtes cachées dans la réalité sont dessinées en pointillés.

Bilan

Tout ce travail étant fait, les élèves ont pu se familiariser avec les différentes représentations d’un pavé droit : en réalité, en perspective et sous forme de patron. Ils ont la possibilité de passer d’une représentation à une autre ce qui représente une gymnastique du cerveau qu’il convient de faire travailler et d’entretenir.

Prolongements ou réinvestissements possibles

Selon le temps dont on dispose, on peut :

• Utiliser ponctuellement un logiciel de géométrie dynamique pour consolider et entretenir les mécanismes de vision dans l’espace (passage de la vision en perspective à l’image mentale de l’objet réel et inversement). À noter que ceci ne doit intervenir qu’après la mise en place de la vision en perspective à partir de l’objet réel.

• Réaliser un cube et/ou un pavé droit par pliage dans une enveloppe 11 cm × 22 cm, à insérer dans le cahier [3].

• Commencer une carte mentale sur le rectangle. En effet, la définition et des propriétés du rectangle ont été réactivées au cours de la description de la boîte et au fur et à mesure de l’année, la carte mentale sera complétée avec de nouvelles découvertes.

• Sur papier quadrillé, représenter deux patrons d’un même pavé puis comparer leurs aire et périmètre. Construire ensuite un autre patron possible.

• Construire un flexacube [4].

• Mettre en place les activités proposées par l’IREM de Paris Nord [5].

• Colorier les patrons des brochures Jeux de l’APMEP [1] : une activité qui, selon que l’on peut ou non plier le patron, permettra de faire travailler le passage de la 2D à la 3D.

Références

1. APMEP. « Jeux école 2 » et « Jeux 5 ». . ↩
2. APMEP. Des patrons téléchargeables. .
3. Didier Boursin et Valérie Larose. Pliages et mathématiques. ACL-Édition. ↩
4. IREM de Clermont-Ferrand. Brochure « Espace et géométrie ». . ↩
5. IREM de Paris-Nord. Brochure « La troisième dimension ». . ↩

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Anne Dusson et Nathalie Lecouturier enseignent respectivement à Petit-Quevilly (76) au collège Fernand Léger et à Rouen (76) au collège Barbey d’Aurevilly.