Bain ou douche ?

L’éducation au développement durable est un des thèmes des différents programmes scolaires. Claude Fahrer nous propose une situation mise en œuvre dans sa classe de Seconde, illustrée de productions d’élèves.
Puis il élargit la réflexion à l’enseignement de la modélisation en collège et lycée, en s’appuyant sur une ressource récente des IREM.

Claude Fahrer

© APMEP Juin 2022

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Une activité sur le développement durable

La fiche suivante de caractéristiques de cette situation est extraite d’une brochure de l’IREM de Strasbourg [1].

1. À quel niveau le problème est-il destiné ?	Le problème est plus particulièrement destiné à des élèves de Troisième ou de Seconde. Il a été testé en classe de Seconde.
2. Déroulement de l’activité.	À la fin d’une séance, j’ai posé la question oralement et nous en avons discuté pendant une dizaine de minutes. Les discussions ont permis d’orienter les recherches à faire pour la prochaine séance. Lors de la séance suivante, un bilan a été fait en classe pendant une dizaine de minutes sur l’état d’avancement des recherches. À la fin de cette deuxième séance, j’ai demandé aux élèves de rédiger à la maison un compte rendu de leurs recherches, dont quelques extraits se trouvent ci-dessous.
3. En quoi est-ce un problème de modélisation ?	Il pose une question issue de la vie réelle à laquelle on essaie d’apporter une réponse argumentée. Pour répondre à ce problème, il est nécessaire de faire des hypothèses simplificatrices qui permettront sa résolution : quel est le débit moyen d’un pommeau de douche, quelle est la contenance d’une baignoire ; quelle est la durée moyenne d’une douche.
Quelles sont les hypothèses et comment les formuler ?	Pour émettre des hypothèses, les élèves ont été obligés de faire des recherches, souvent sur l’internet. Certains ont d’ailleurs cité leurs sources .
4. Compétences mathématiques visées	La situation fait intervenir des grandeurs composées (débit en L/min) et éventuellement des connaissances sur les fonctions affines. Plusieurs élèves ont utilisé des fonctions affines pour déterminer la «durée de basculement».
5. Point de vue du professeur	L’activité a nécessité peu de temps en classe (une vingtaine de minutes). Elle a suscité de l’intérêt et de la curiosité chez tous les élèves (y compris les plus fragiles) qui ont rédigé des comptes rendus plus personnels que les devoirs maison habituellement rendus.

Quelques comptes rendus d’élèves

Copie n° 1

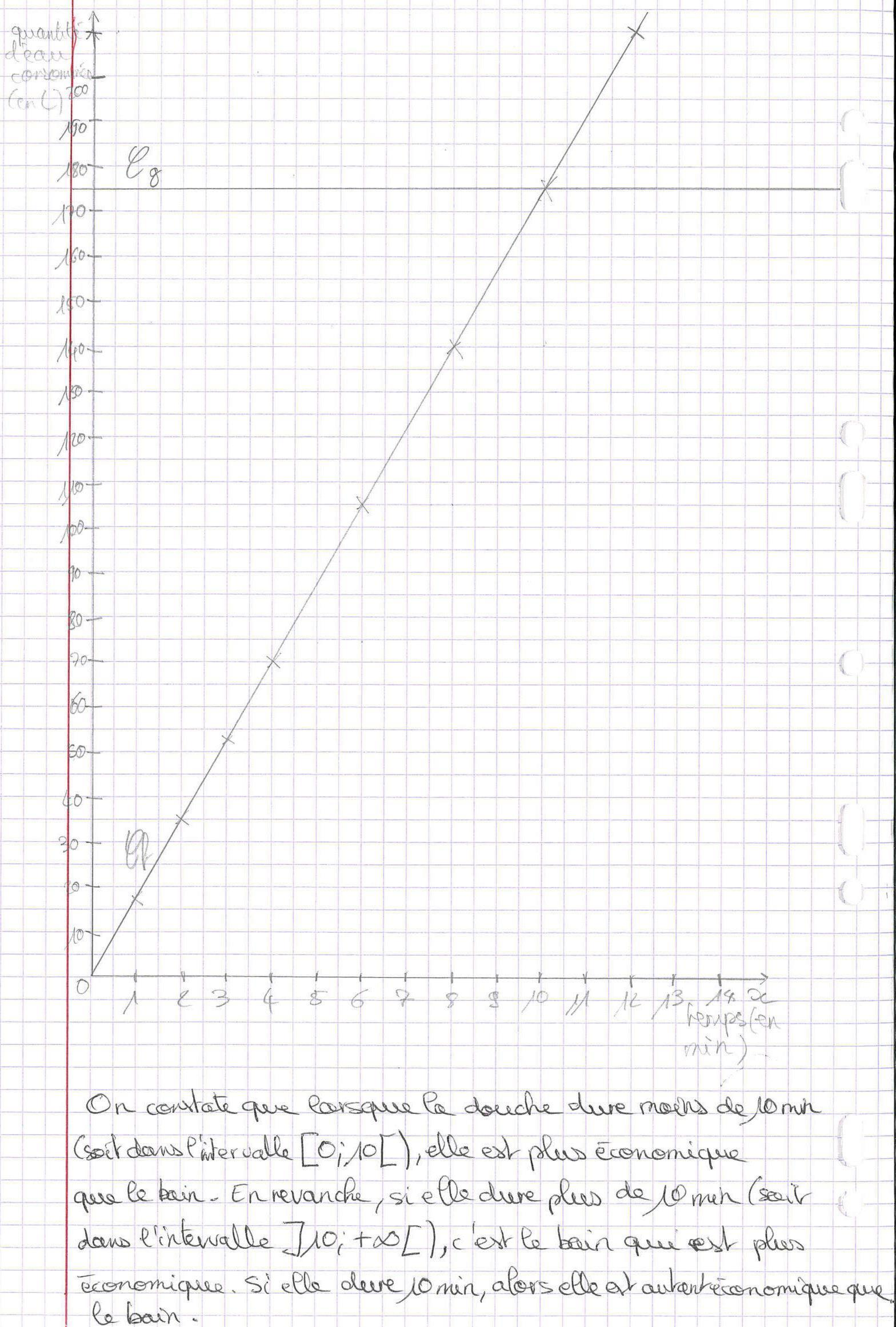
Commentaire

L’élève repère bien des hypothèses à formuler. Par exemple, le débit moyen d’une douche mesuré en  et la consommation moyenne d’un bain sont justifiés par des données récupérées d’un site scientifique, celui du CNRS. Le modèle mathématique choisi permet la comparaison de ces consommations en représentant graphiquement ces consommations en fonction des durées de consommation d’un bain et d’une douche. Avec ce modèle, il résout le problème posé, montrant qu’une douche rapide consomme moins d’eau qu’un bain, ce qui permet de sensibiliser aux moyens d’économiser la consommation d’eau.

Copie n° 2

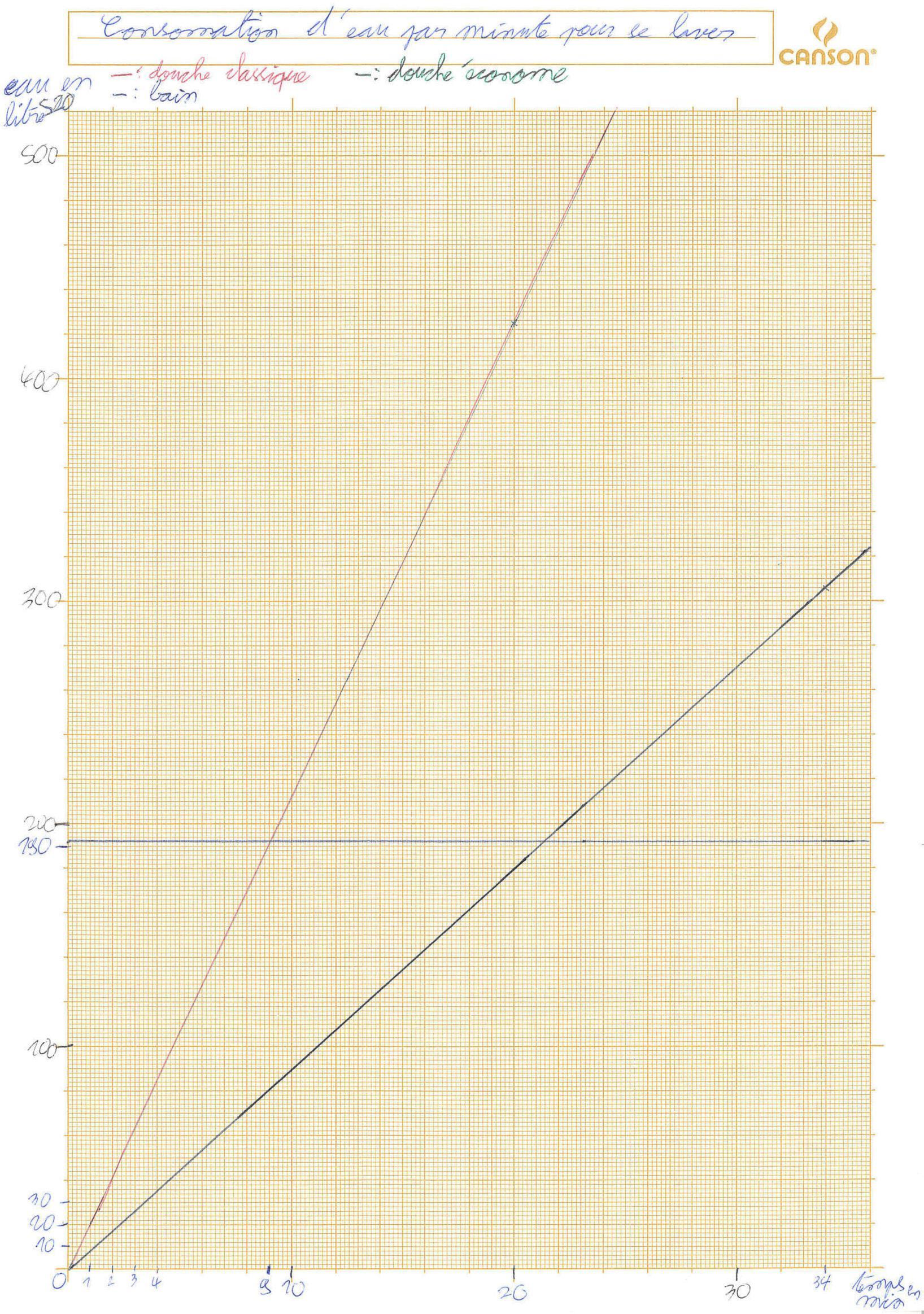
Commentaire

Les hypothèses sont plus fines que pour l’élève précédent puisque deux types de douches sont envisagés: la douche classique et la douche économe. Cependant, l’argumentation extra-mathématique pour fonder cette typologie est absente et on ne sait pas d’où viennent les données repérées par l’élève, ni comment il caractérise ces types de  douche. Il convient de sensibiliser les élèves à la nécessité d’argumenter les choix d’hypothèses, même si ceux-ci reposent sur des arguments extra-mathématiques de connaissances en lien avec le monde réel.

Copie n° 3

Commentaire

Cet élève, tout comme le précédent, propose des hypothèses sur les données de consommation d’une douche ou d’un bain qui ne sont pas justifiées. Sa décision ne se fonde pas sur un calcul précis. Au lieu d’indiquer une consommation moyenne en litres, il indique un intervalle, pour le bain comme pour la douche, ce qui rend la comparaison difficile. Il mentionne ensuite la durée, 30 minutes pour une douche, ce qui peut paraître bien long, sans expliquer d’où vient cette donnée et en quoi elle permet de justifier un choix. Ici, aucun modèle mathématique clair n’apparaît pour justifier la décision finale. Alors que les précédentes comparaisons mettaient en évidence clairement les seuils de décision ( pour la copie 1; et pour la copie 2), ici ils n’apparaissent pas clairement justifiés.

L’examen des deux premières copies montre clairement que le choix des hypothèses influe grandement sur la solution trouvée, même si le même modèle mathématique est utilisé (comparaison graphique des consommations en fonction du temps).

Modéliser avec les élèves

L’activité précédente illustre un travail de modélisation mathématique avec des élèves. Nous allons nous appuyer sur la brochure de l’IREM de Strasbourg [1], qui fera l’objet d’une prochaine recension dans la revue, pour développer quelques points de vigilance concernant la modélisation par les élèves.

Deux éléments nous apparaissent importants dans le processus de modélisation.

• D’une part, les données de la situation doivent être précisées. Ces données peuvent être explicitement proposées par l’énoncé. Par exemple, dans notre problème, il est demandé de comparer d’un point de vue économique le bain et la douche. Il ne s’agit donc pas de se placer du point de vue du degré de satisfaction, du point de vue médical ou autre. Parfois il faut aller chercher les données évoquées implicitement par l’énoncé. Par exemple, si l’énoncé avait indiqué se référer aux données de consommation d’un bain et d’une douche précisées dans un article d’un numéro de la revue Au fil des maths, il aurait fallu se référer à cette revue pour expliciter ces données. Mais il y a aussi les données supplémentaires que le résolveur du problème ajoute: c’est ce que nous appelons «hypothèses» pour les distinguer des données implicites ou explicites de l’énoncé. Dans nos exemples, le résolveur de la copie 1 suppose une consommation de \({17,5}L/min\) pour une douche et de \({175}L\) pour un bain. Les résolveurs des copies 2 et 3 font d’autres hypothèses. Autant les données de l’énoncé sont admises (même si elles peuvent être critiquées), autant les hypothèses du résolveur doivent être argumentées, par des arguments extra-mathématiques (expérience personnelle, connaissances sociales…) ou par des arguments mathématiques (données statistiques relevées dans une revue scientifique…). Il est donc important de préciser les données de l’énoncé, les hypothèses des résolveurs et les arguments qui les sous-tendent.

• D’autre part, la phase de choix et d’application du modèle est essentielle. Elle dépend bien entendu des modèles disponibles chez l’élève, ce qui est lié au niveau de la classe auquel le problème est proposé. Ici le modèle fonctionnel proposé par la copie 1, utilisant la consommation d’eau de la douche en fonction du temps en la comparant à celle du bain, qui est une fonction constante en fonction du temps, est disponible chez les élèves de Seconde. En revanche, un autre modèle, qui reposerait sur des équations différentielles, ne serait pas mobilisable en Seconde. Pour défendre le modèle choisi, comme évoqué précédemment, des arguments extra-mathématiques ou mathématiques peuvent être discutés. Ensuite, il faudra bien vérifier l’application correcte du modèle (le respect des conditions d’utilisation du modèle, la correction des calculs…). Enfin, dans certains cas, la confrontation de la réponse trouvée aux conditions de la réalité pourra faire apparaître un manque de vraisemblance de la solution proposée. Par exemple, si l’élève de la copie 1 avait trouvé que le bain était plus intéressant que la douche seulement après une douche de plus d’une centaine d’heures, il aurait intérêt à chercher une erreur (dans les représentations ou lectures graphiques ou autres). De manière générale, un retour réflexif sur le choix des hypothèses et du modèle permettra une éventuelle modification de ce choix pour mieux l’adapter aux conditions de la réalité.

Le bilan de cette activité montre qu’il est possible de mettre en œuvre des activités de modélisation en lien avec les différentes parties du programme et qui ne prennent pas trop de temps. L’expérience a montré l’intérêt des élèves pour ce type de recherche, même chez des élèves habituellement peu motivés. Le thème du développement durable permet de travailler à la fois sur la citoyenneté et l’esprit critique dans sa formation extra-mathématique, ainsi que sur la compétence de modélisation dans sa formation mathématique. Il est important de discuter des arguments pour mieux distinguer mathématique et extra-mathématique.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Claude Fahrer est professeur de mathématiques au lycée Marc-Bloch de Bischheim et animateur à l’IREM de Strasbourg.