\(\def\num#1{#1}\)
Dérive génétique et autres forces évolutives
Dans l’activité sur la dérive génétique, on a pu constater que pour une taille de population suffisamment grande, les fréquences alléliques étaient relativement stables au cours des générations. Ceci mène naturellement à l’étude du modèle de Hardy-Weinberg. Il est étudié en enseignement scientifique de Terminale mais d’un point de vue mathématique, il peut être démontré en spécialité mathématiques dès la classe de Première.
Jean-Louis Marcia
© APMEP Décembre 2021
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Le modèle de Hardy-Weinberg dès la classe de Première
Énoncé du modèle
|
Sous les hypothèses suivantes (voir la ressource Eduscol sur l’enseignement scientifique de Terminale) :
On établit que les fréquences alléliques sont stables à partir de la génération \(0\) et les fréquences génotypiques quant à elles le sont à partir de la génération \(1\). |
La version 1 du devoir maison
Après avoir abordé le chapitre relatif aux probabilités conditionnelles et à l’indépendance, un devoir maison peut être suggéré aux élèves de Première. Il y a deux façons de mettre en place le modèle de Hardy-Weinberg.
La première, plus naturelle pour les élèves, fait l’objet de la version 1 du devoir (DM 1).
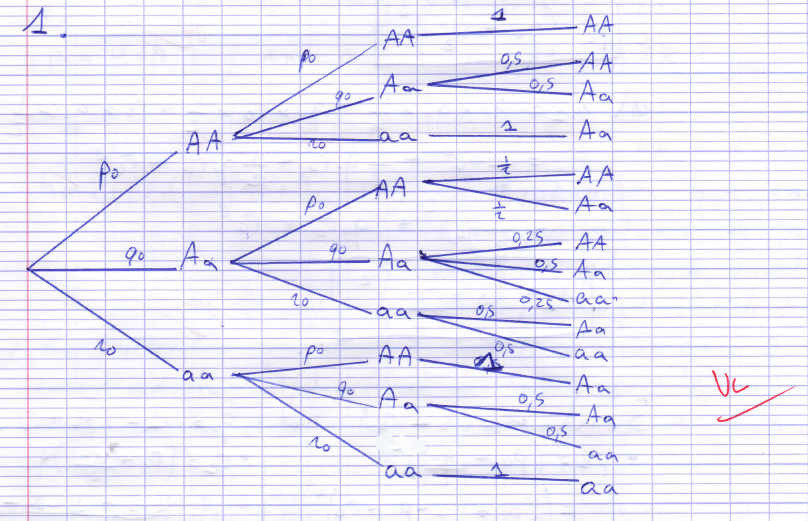
Dans un premier temps, on met en place la stabilisation génotypique au cours des générations. Le raisonnement repose sur la rencontre au hasard de deux individus de la population et à partir de leurs génotypes possibles (figure 1), la formule des probabilités totales donne la distribution génotypique chez l’enfant.
À partir de cette nouvelle génération, on réitère le raisonnement pour obtenir la distribution génotypique de la génération suivante et on constate qu’elle est identique à la précédente.
Reste ensuite à faire le lien entre distribution génotypique et distribution allélique pour conclure également à sa stabilisation au cours des générations.
Comme le calcul algébrique y tient une place importante ; ce qui est l’occasion de faire progresser les élèves dans ce domaine même si on peut reprocher à cette version la lourdeur des calculs.
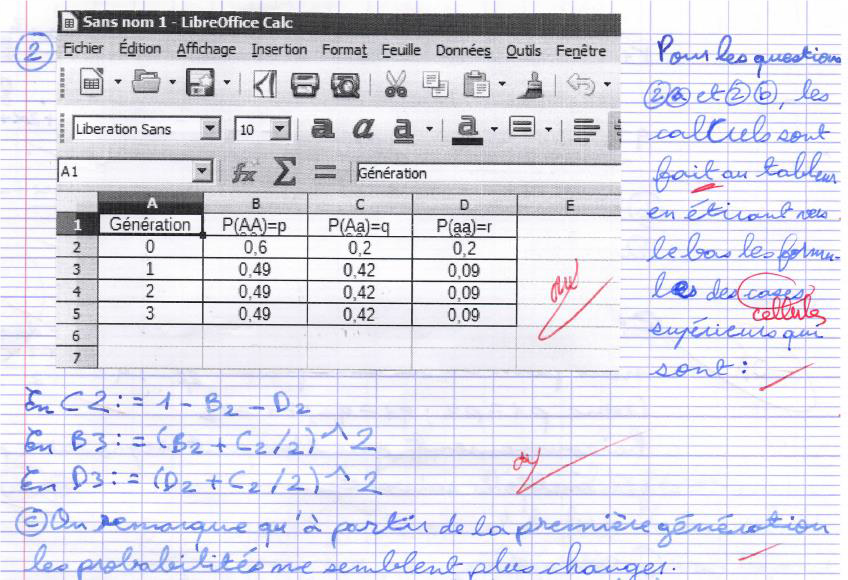
L’utilisation du tableur (figure 2), montre aux élèves son importance dans la recherche en l’occurrence pour faire apparaitre des propriétés et émettre des conjectures.
En particulier, on constate ici que la fréquence des génotypes est stable après la première génération.
La version 2 du devoir
La version 2 du devoir (DM 2) a l’avantage de supprimer la lourdeur des calculs algébriques évoqués précédemment. C’est d’ailleurs la démarche adoptée en général dans l’enseignement supérieur lors de l’étude théorique du modèle en génétique des populations. Mais le raisonnement concernant la stabilisation allélique peut dérouter, voire être une source de confusion (et c’est sur ce point que les élèves d’enseignement scientifique de Terminale pourront rencontrer des difficultés). En effet, on met en place la distribution génotypique de l’enfant à partir de la rencontre au hasard de deux allèles dans la population. Cette approche s’affranchit des individus et considère la reproduction comme une « rencontre de deux allèles issus de la population ». Cela se justifie par la notion d’indépendance d’événements, indispensable ici et qui était simplement sous-entendue dans la version 1 du devoir mais qui, en y regardant de plus près, apparaissait dans le résultat simplifié des formules établies.
Et pour preuve, dans cette version 1, on établit la formule : \(p_1=\left (p_0+\dfrac {q_0}{2}\right )^2\), qui traduit le fait que \(p(\mathrm {AA})=p(\mathrm {A})\times p(\mathrm {A})\), en d’autres termes, la probabilité que le génotype de l’enfant soit AA est égale au produit des probabilités que chaque allèle « choisi » soit A. Ce qui prouve l’indépendance et valide le raisonnement. D’autre part, la version 2 privilégie la notion de suites numériques et leur donne ainsi toute légitimité aux yeux des élèves. En particulier, les élèves sont amenés à établir et à manipuler des relations de récurrence, ce qui constitue bien souvent un obstacle pour eux.
Si l’activité de dérive génétique a été traitée en Seconde, on peut espérer que les élèves puissent plus facilement argumenter. Sinon ce peut être l’occasion de leur proposer d’étudier ou simplement d’exécuter le programme Python pour constater l’écart au modèle. On pourra dans ce cas faire usage des listes pour générer les points du graphique.
Cette simulation confirmerait alors l’hypothèse émise en fin de devoir sur le caractère fini de la population et le phénomène de dérive génétique que cela entraîne.
Les autres forces évolutives
Le modèle de Hardy-Weinberg est également étudié en Terminale dans le cadre de l’enseignement scientifique et de la spécialité SVT. Même s’il n’a pas de réalité biologique, il est à la base du raisonnement pour émettre certaines hypothèses en dynamique des populations. En particulier, si les données observées sur les fréquences génotypiques ne respectent pas l’équilibre du modèle, on conclura qu’une force évolutive s’exerce sur la population. Reste ensuite à déterminer laquelle (deux exercices et leurs corrigés montrant un cas où il n’y a pas d’écart alors qu’avec l’autre si).
Les mutations génétiques
Les mutations génétiques s’exercent sur les allèles du gène considéré. Elles se font au hasard, soit spontanément soit sous l’action d’agents mutagènes. La probabilité de mutation d’un allèle est donc variable.
L’activité Dérive génétique et mutations proposée en Activité 1 rappelle le programme de l’activité de dérive génétique. La seule différence se situe au niveau de la représentation graphique où les points sont générés par une liste conformément aux compétences de Première et Terminale en algorithmique.
Pour simuler ces mutations, on demande aux élèves de définir la fonction mut. Elle doit s’appliquer sur chaque allèle d’une population \(P\) avec une fréquence \(f\).
Pour simplifier la représentation graphique, les allèles mutés seront regroupés sous un seul allèle noté ’a’.
Des exécutions successives de cette fonction sur une population fixée comme [[’v’, ’v’], [’m’, ’m’], [’v’, ’v’], [’v’, ’v’], [’v’, ’v’], [’v’, ’m’]] par exemple, permettra aux élèves de constater son effet et les aidera à l’intégrer dans le programme. En particulier, on peut espérer qu’ils pensent à modifier ensuite la fonction Dist et le corps du programme pour y intégrer ce nouvel allèle et sa distribution (programme 1).
Il ne reste plus qu’à exécuter le programme modifié.
Dans un premier temps, on choisit de fixer le nombre de couples \(n\) et le nombre de génération \(g\) et de faire varier la fréquence \(f\) de mutation d’un allèle.
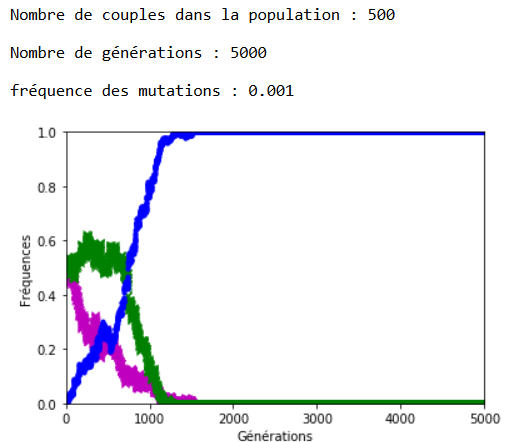
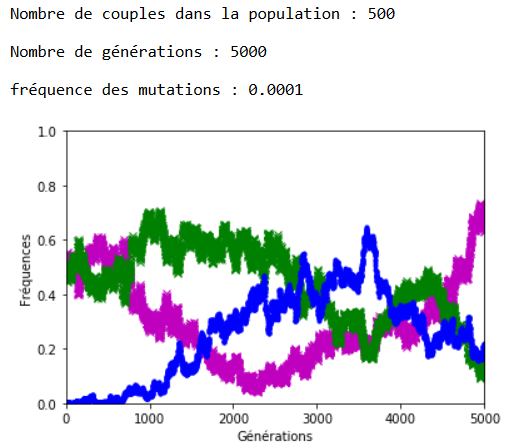
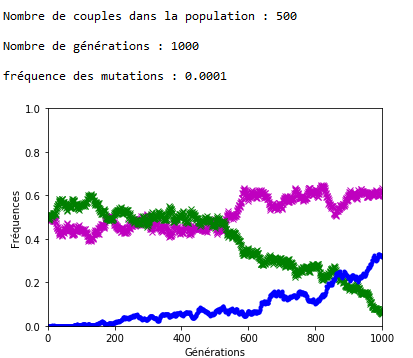
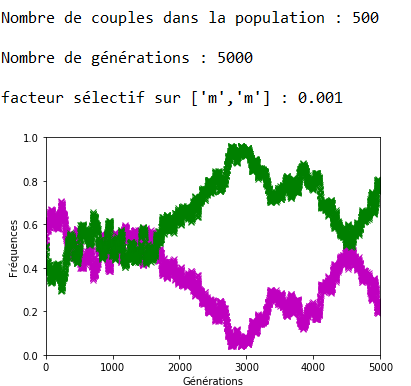
Après plusieurs exécutions avec les mêmes valeurs des paramètres, il apparaît qu’une valeur de 0,001 pour \(f\) entraîne l’extinction des allèles d’origine assez rapidement (tout est relatif) et qu’avec \(f = \num {0,0001}\) les allèles d’origine cohabitent avec les allèles mutés sur la période étudiée, à ceci près que la dérive génétique continue à s’exercer et peut contrer momentanément la progression des allèles mutés (figures 4 et 51).
Malgré la dérive génétique, et si les mutations perdurent, la disparition des allèles d’origine semble inéluctable. On peut l’observer en fixant la valeur de \(n\) et de \(f\), et en faisant varier le nombre de générations \(g\) (figures 6 et 7).
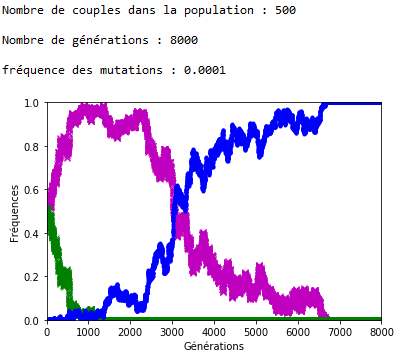
Figure 7. En attendant l’extinction des allèles d’origine (ex. 2).
On peut faire remarquer ici aux élèves de spécialité mathématiques et mathématiques complémentaires que, si on ne tenait pas compte de la dérive génétique, d’une génération à la suivante, les allèles d’origine perdraient \(f\) fois leur effectif ; ce que l’on pourrait également traduire par une relation de récurrence du type \(\mathrm {O}(g+1)=\mathrm {O}(g)-f\times \mathrm {O}(g)=(1-f)\times \mathrm {O}(g)\), où O est l’effectif des allèles d’origine à une génération \(g\). Cette remarque permettrait par exemple de prévoir le temps nécessaire à leur extinction en résolvant l’inéquation \((1-f)^g<\dfrac {1}{2N}\) à l’aide de la fonction \(\ln \) 2.
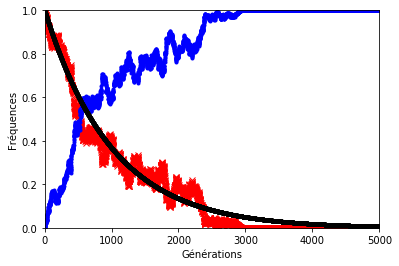
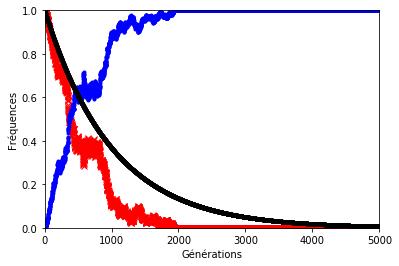
Le résultat n’est pas forcément très éloigné de ce que l’on observe sur les graphiques précédents sauf lorsque le hasard s’en mêle (figures 8, 9 et 10). En effet, le hasard qui est à l’origine de la dérive génétique, peut exercer une pression telle qu’elle éloignerait la décroissance des allèles d’origine du modèle géométrique.
Pour illustrer cela, on a représenté ci-dessous la fréquence des allèles d’origine avec et sans dérive génétique. Les paramètres sont les mêmes que précédemment.
Dans les graphiques ci-dessous, la décroissance géométrique est représentée en noir, la fréquence des allèles d’origine en rouge et celle des allèles mutés en bleu.
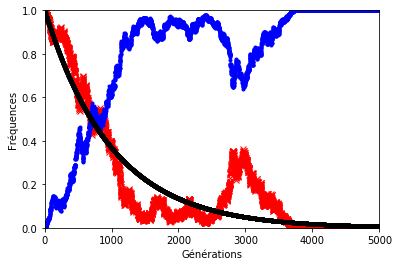
Figure 10. . . . sauf lorsque le hasard s’en mêle (ex. 2) !
Mais tout ceci est sans tenir compte de la sélection naturelle.
La sélection naturelle
L’environnement exerce une pression sur les individus d’une population. Il va sélectionner les individus adaptés à cette pression et au contraire désavantager les autres ; c’est ce qu’on appelle la sélection naturelle.
L’activité Dérive génétique et sélection naturelle (Activité 2) présente la fonction selec qui s’applique à une population \(P\) d’effectif pair. Elle simule la sélection naturelle que peuvent subir certains phénotypes.
On choisit ici de simuler une sélection défavorable au phénotype associé au génotype [’m’, ’m’] (c’est-à-dire les tortues à carapace marron) en le faisant disparaître de la population avec une fréquence \(s\).
La conséquence de cela est que l’effectif de la population n’est plus constant au cours des générations. D’un point de vue algorithmique, pour rester sur le principe de la formation des couples par tirage sans remise, on choisit d’imposer artificiellement de maintenir l’effectif pair en créant si besoin un « survivant » parmi les individus [’m’, ’m’].
Ici certains élèves découvrent alors la fonction % renvoyant le reste de la division euclidienne d’un entier \(a\) par un entier \(b\) non nul.
Quelle sera l’influence de cette sélection, et en particulier du choix de la valeur de \(s\), sur l’évolution des fréquences alléliques sur une période donnée ? Ou bien, pour \(s\) fixé, combien de générations faudra-t-il attendre pour voir l’allèle ’m’ disparaître ? La réponse n’est pas si évidente si on tient compte de la dérive génétique (voire des mutations).
Il ne reste plus qu’à intégrer cette fonction au programme de dérive génétique. Il suffit de placer la fonction Selec juste après la fonction Pop_suivante dans le programme (programme 2).
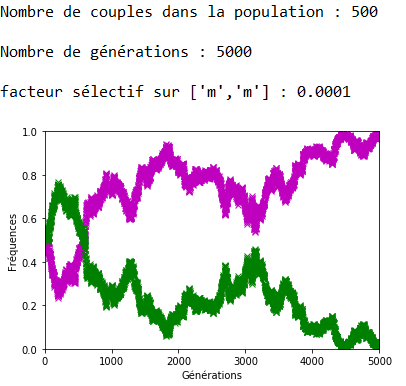
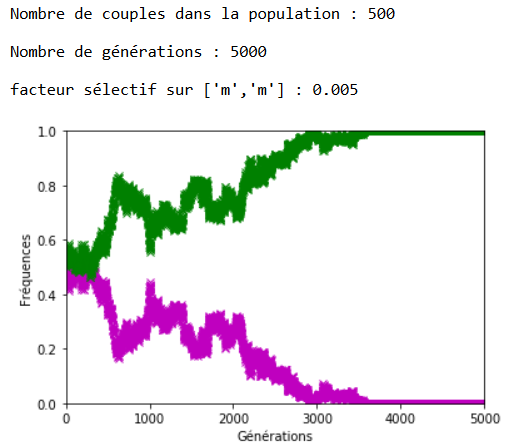
Lorsque \(s\) est faible, la dérive génétique peut l’emporter sur la sélection naturelle comme l’indique la figure 12 où l’allèle ’m’, soumis à une sélection défavorable, voit malgré cela sa fréquence se fixer à \(1\).
Lorsque \(s\) augmente, l’effet s’inverse et on note bien sur les figures 13, 14 et 15 la rapidité de l’extinction de l’allèle ’m’ en fonction de l’intensité du facteur sélectif.
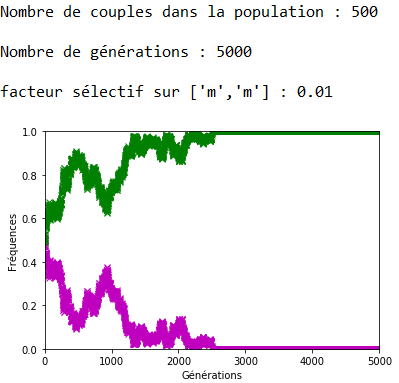
Figure 15. La sélection naturelle l’emporte sur la dérive génétique (ex. 2).
Il est plus difficile ici d’évaluer le temps nécessaire à la disparition de l’allèle ’m’ car il apparaît aussi dans le génotype m//v qui n’est pas soumis à la sélection. Il faudra alors attendre son extinction.
Appariement non aléatoire : les préférences sexuelles
On peut envisager le cas où un phénotype va induire une préférence dans le choix du partenaire. Les appariements ne sont plus équiprobables.
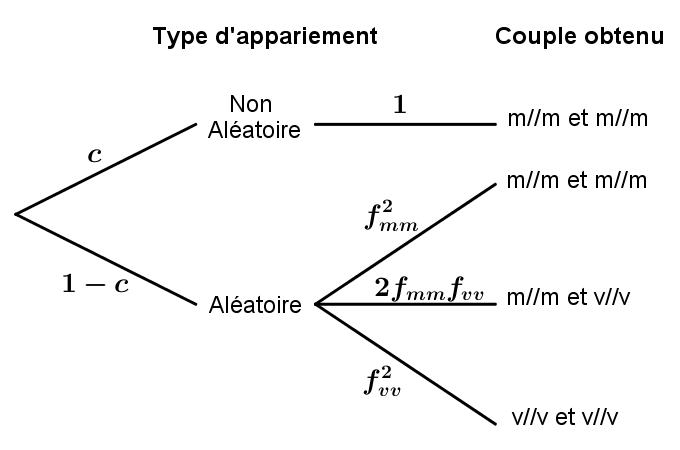
Par exemple, on peut choisir de forcer l’appariement en priorité entre les individus [’m’,’m’] avec une fréquence \(c\).
Afin de simuler ce processus on met en place l’algorithme suivant :
-
dans un premier temps, et avec une fréquence \(c\), on choisit un individu [’m’,’m’] dans la population, s’il existe !
-
ensuite, on choisit un deuxième individu [’m’,’m’], s’il existe encore, et on reproduit le couple ainsi formé en créant les deux descendants (il est clair ici que les descendants seront de génotype m//m
mais cette étape pourra être utilisée en cas d’appariement de génotypes différents) ; -
dans les autres cas on procède à la reproduction des individus de façon équiprobable ;
-
on réitère le processus jusqu’à vider la population.
Dans l’activité Dérive génétique et appariement non aléatoire (Activité 3) on demande de modifier la fonction Pop_suivante du programme de dérive génétique afin de respecter l’algorithme présenté ci-dessus.
On propose simplement de compléter la nouvelle fonction car les modifications sont importantes mais on peut également faire le choix de laisser les élèves la concevoir ou au contraire de la leur donner et contrôler qu’ils l’ont bien comprise en posant des questions sur le rôle de telle ou telle ligne.
Il n’y a plus ensuite qu’à l’intégrer dans le programme et l’exécuter (programme 3).
On a modifié l’urne U de la fonction Pop en ajoutant un allèle ’m’ pour faire passer sa fréquence dans la population à \(\dfrac {2}{3}\cdotp \) Ce choix totalement arbitraire aide à mieux distinguer son évolution sur les graphiques.
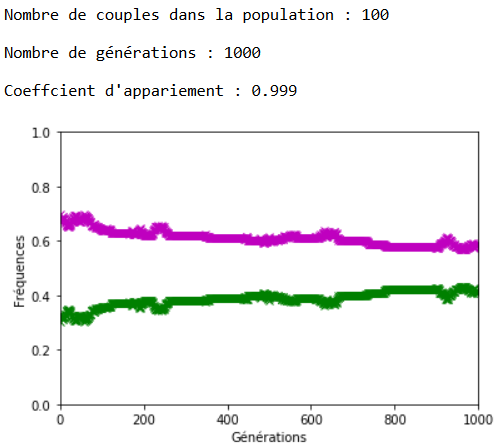
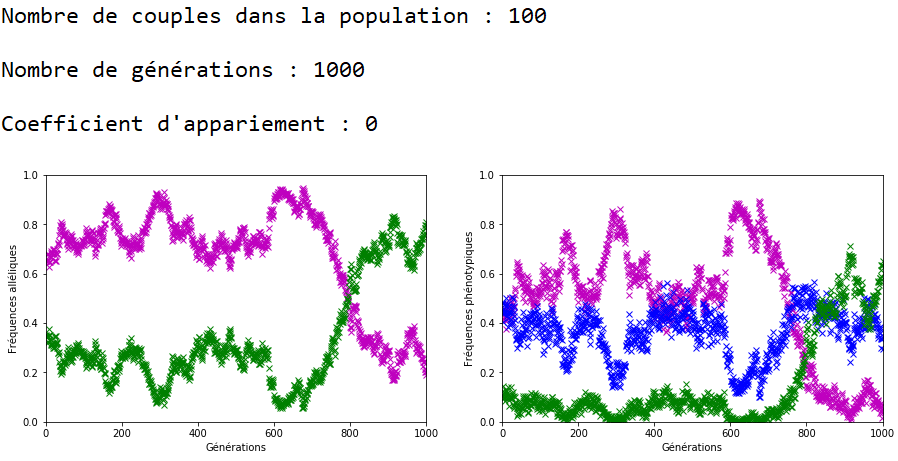
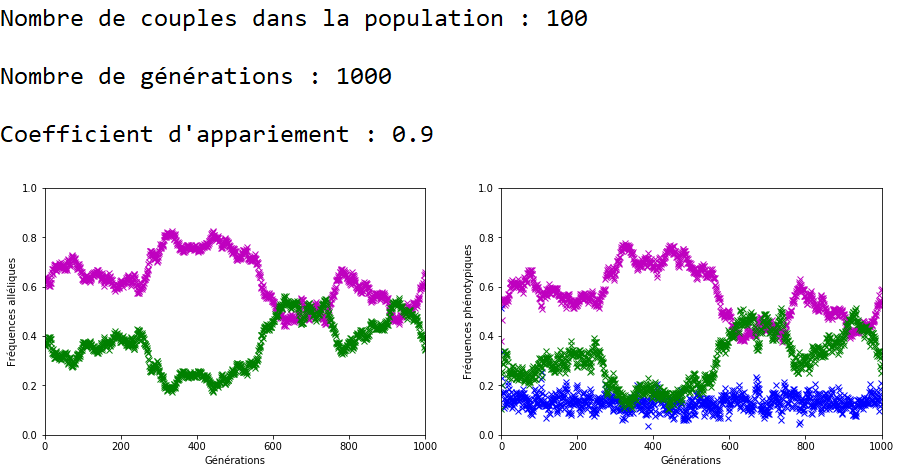
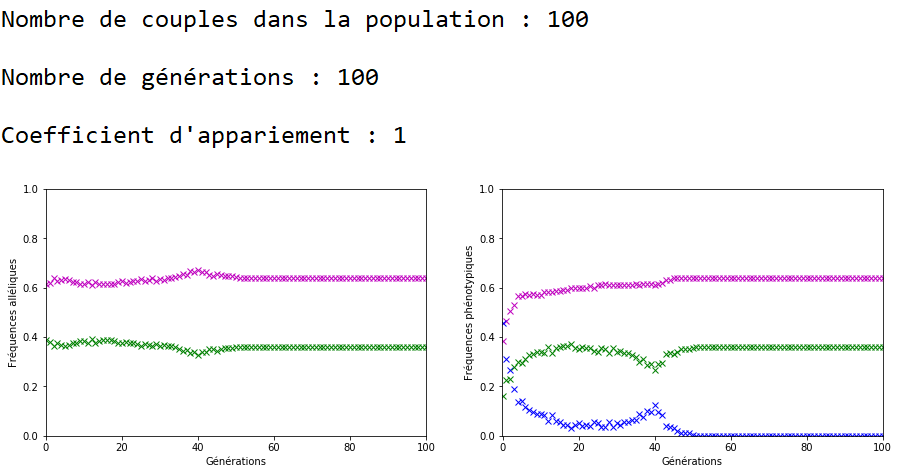
On décide de fixer les valeurs de \(n\) et \(g\) et de faire varier celle du coefficient d’appariement \(c\).
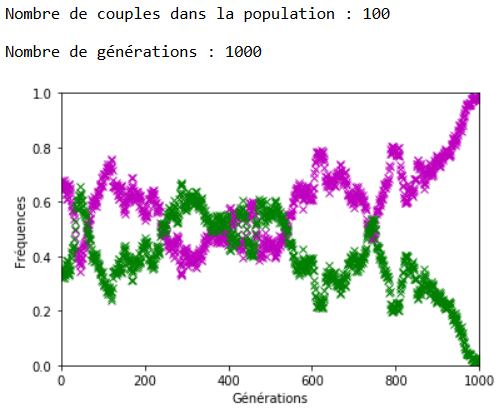
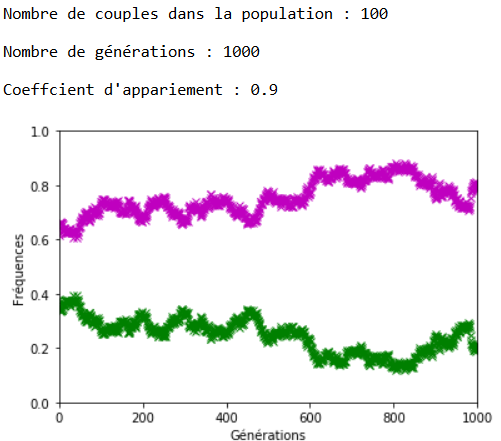
À l’inverse des mutations, il faut que le coefficient \(c\) soit très fort pour constater un effet sur l’évolution des fréquences alléliques (figures 16, 17 et 18).
On constate qu’un fort coefficient d’appariement estompe la dérive génétique. Les fréquences alléliques sont globalement stables voire constantes sur quelques générations (un coefficient extrême de \(c=1\) rend ces fréquences définitivement constantes après quelques générations).
Qu’est ce qui peut expliquer un tel résultat?
Pour répondre à cette question l’activité Dérive génétique et phénotype (Activité 4) s’intéresse aux phénotypes.
On rappelle que dans notre exemple des tortues, le phénotype marron est associé au génotype m//m, le phénotype vert au génotype v//v et le phénotype beige au génotype m//v.
Pour des raisons purement pratiques nous noterons ces phénotypes respectivement ’M’, ’V’ et ’B’ avec les
couleurs graphiques respectives Mauve, Vert et Bleu.
La fonction suivante traduit le génotype en phénotype. Cette fonction a d’abord un objectif didactique en SVT : il ne faut pas confondre génotype et phénotype (même si, ici, ils sont en bijection). D’autre part, cette fonction permet de modifier facilement le contexte dans le cadre d’un allèle récessif où par exemple m//m et m//v donnent M et seul v//v donne V (il n’y a dans ce cas que deux phénotypes).
Il ne reste plus qu’à l’intégrer au programme précédent en modifiant la fonction Dist et les listes graphiques pour obtenir la représentation graphique des phénotypes au cours des générations (programme 4).
On peut ainsi mettre en vis-à-vis l’évolution des fréquences alléliques et des fréquences phénotypiques.
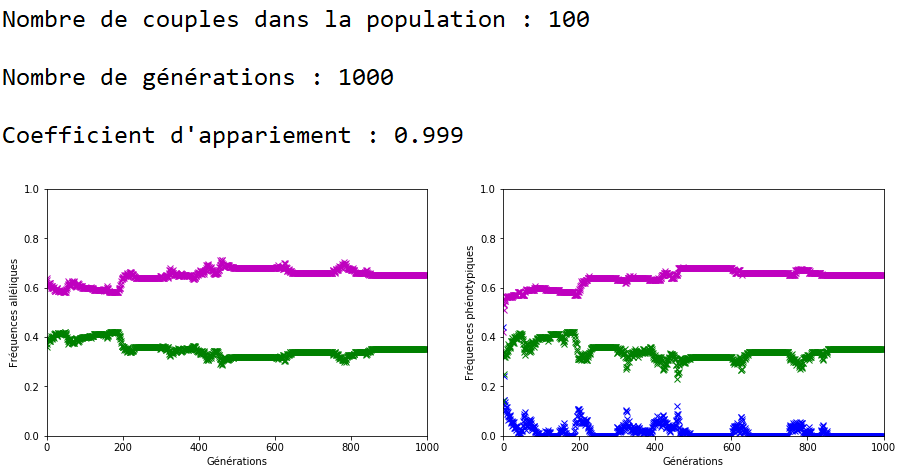
Dans le cas d’un appariement non aléatoire fort (figure 22), le phénotype beige (en bleu) associé au génotype m//v disparaît de la population au bout de quelques générations. Il ne reste plus que des individus homozygotes (m//m et v//v) dans la population et donc les fréquences alléliques restent stables jusqu’à ce qu’au moins un nouvel individu m//v apparaisse. Ceci peut prendre quelques générations car la valeur de \(c\) est forte et les appariements se font essentiellement entre individus m//m et entre individus v//v.
Ensuite, il faut attendre à nouveau l’extinction des tortues à carapace beige et le cycle recommence.
Pour les spécialistes, il serait intéressant d’évaluer la probabilité \(p\) du succès : « au moins un nouvel individu m//v apparaît après la reproduction de la population » (en fait, au vu de l’algorithme, les individus sont créés deux par deux donc il y aura au moins deux individus m//v), puis de déterminer le temps d’attente moyen pour voir ce succès apparaître pour la première fois. Sur la période où les fréquences alléliques sont stables, on est alors dans le cadre d’une loi géométrique.
On se place donc au moment où les génotypes m//v ont disparu. Dans le cas de tirages avec remise pour former les couples, l’expérience revient à répéter \(n\) fois de façon indépendante l’épreuve modélisée par l’arbre de la figure 24.
Sachant qu’il n’y a plus d’individu m//v, on obtient, \(p=1-\bigl (1-2(1-c)f_{\texttt {mm}}\,f_{\texttt {vv}}\bigr )^n\), où \(f_{\texttt {vv}}\) et \(f_{\texttt {mm}}\) sont les fréquences respectives des génotypes v//v et m//m juste après l’extinction du génotype m//v.
Les fréquences étant stables pendant la période cherchée, on peut appliquer l’espérance de la loi géométrique pour obtenir en moyenne \(\dfrac {1}{p}\) générations pour voir le succès apparaître pour la première fois.
Une application numérique avec \(n=100\text { couples}\), \(f_{\texttt {vv}}=\num {0,3}\) ; \(f_{\texttt {mm}}=\num {0,7}\) et \(c=\num {0,999}\) donne environ \(24\) générations.
Sachant qu’il s’agit d’une moyenne et qu’en réalité les fréquences des génotypes dépendent de la période étudiée, on peut confronter ce résultat à la simulation du programme 5.
Un autre aspect intéressant est que, malgré cette quasi stabilisation des fréquences, les valeurs de l’équilibre du modèle de Hardy-Weinberg ne sont pas respectées. En effet les fréquences génotypiques attendues par le modèle sont ici \(\dfrac {4}{9}\), \(\dfrac {4}{9}\) et \(\dfrac {1}{9}\) pour les génotypes respectifs m//m, m//v et v//v et on constate que ce n’est pas le cas puisque la fréquence des génotypes m//v est le plus souvent très faible, voire nulle.
Enfin, n’oublions pas non plus que la dérive continue d’agir et que malgré son affaiblissement en cas d’appariement non aléatoire fort (et non extrême), on peut supposer qu’elle finira par faire disparaître l’un des deux allèles.
Il reste une force évolutive qui n’a pas été considérée mais qui n’apporte rien de nouveau d’un point de vue algorithmique ; il s’agit des migrations dont l’effet est soit de fragmenter la population soit d’apporter de nouveaux allèles.
Ensemble des annexes de la revue numérique
Jean-Louis Marcia est professeur de mathématiques au lycée Pablo Picasso de Fontenay-sous-Bois et membre du groupe de travail Maths/SVT de l’IREM Paris Nord.
![]()
1.Sur les graphiques (figures 4, 5, 6 et 7), les fréquences des allèles ’m’ et ’v’ sont représentées respectivement en mauve et en vert ; celle de l’allèle ‘a’ est représentée en bleu.
2.On obtient \(g>\dfrac {\ln \left (\dfrac {1}{2N}\right )}{\ln (1-f)}\cdotp \)