Escape Game, des révisions revisitées

À l’approche des examens, les dernières séances de l’année sont souvent consacrées aux révisions. Évidemment, on peut profiter du travail mené par l’APMEP et consulter toutes les annales disponibles en ligne. Hélas, dans certaines classes, il arrive que les élèves se dispensent de ces dernières heures, préférant réviser chez eux (avec plus ou moins de succès). Fabien Aoustin vous propose de les retenir avec un grand jeu.

Fabien Aoustin

© APMEP Mars 2019

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

La séance décrite ci-dessous s’est déroulée une semaine à peine avant la fin officielle des cours en terminale S. En entrant dans la salle, les élèves ont pu se mettre autour d’un grand îlot sur lequel étaient disposés en vrac tous les documents nécessaires au jeu. Une fois installés, sans avoir le droit de toucher aux documents, ils ont pu visionner une petite vidéo expliquant les règles du jeu sur fond de musique de film d’action.

Sur le bureau du professeur est alors dévoilée une valisette fermée avec les cinq cadenas mentionnés dans la présentation du jeu. C’est parti !

Phase de découverte

Dans un premier temps, les élèves découvrent tous les documents mis à leur disposition et se répartissent en cinq groupes, un pour chaque code. Cette phase demande une certaine capacité de communication entre les élèves. De plus, certains documents sont fournis en plusieurs exemplaires identiques afin qu’aucun élève ne se retrouve sans matériel pour réfléchir et travailler.

Première énigme : calculs et logique

Le premier code s’obtient en complétant la grille de nombres croisés ci-dessous. Les calculs sont assez simples mais il est nécessaire de mener à bien quelques raisonnements pour la compléter en entier.

Pour déterminer les quatre chiffres du cadenas doré, il faut ensuite superposer dans le bon sens les quatre transparents suivants.

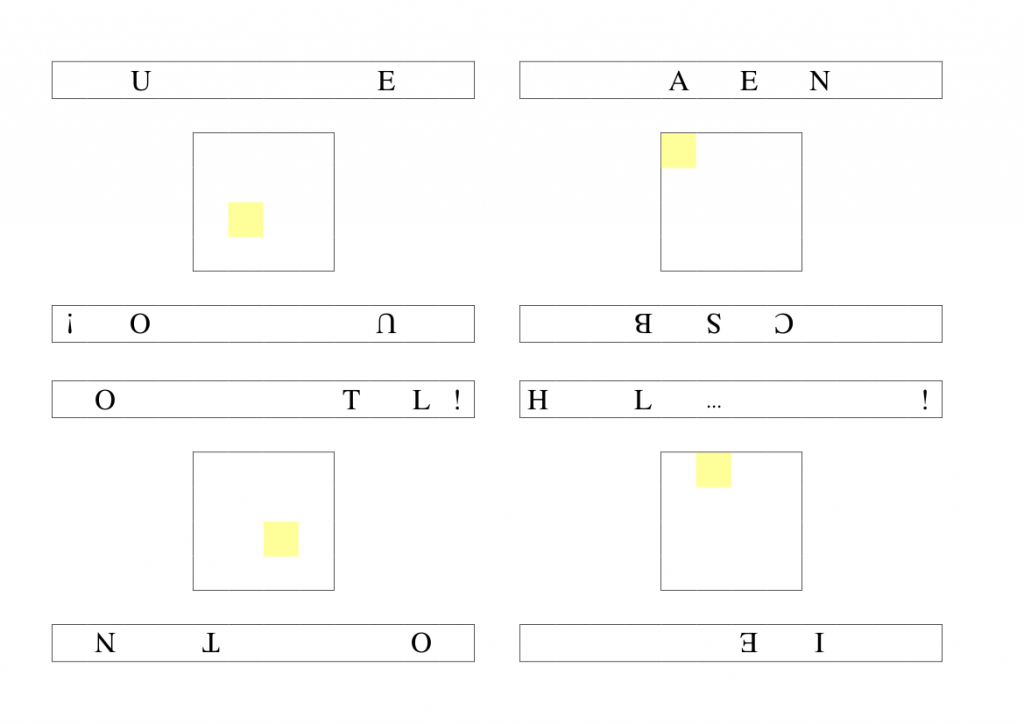
La bonne combinaison fait apparaître le message «OUI C’EST BON !» et on lit alors le code \(8.7.6.4.\) (dans le sens de lecture habituel). Les quatre transparents peuvent aussi faire apparaître le message suivant : «HOULA ET NON !».

Deuxième énigme : nombres complexes

Pour ce deuxième défi, les élèves disposent d’une carte des États-Unis, d’une grille (en mode polaire) imprimée sur une feuille transparente, d’un arbre généalogique des Capétiens (pour l’aide culturelle) et du texte énigmatique suivant :

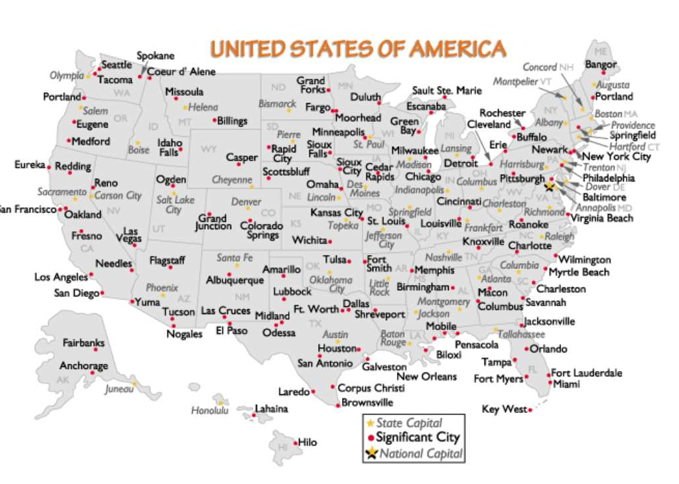
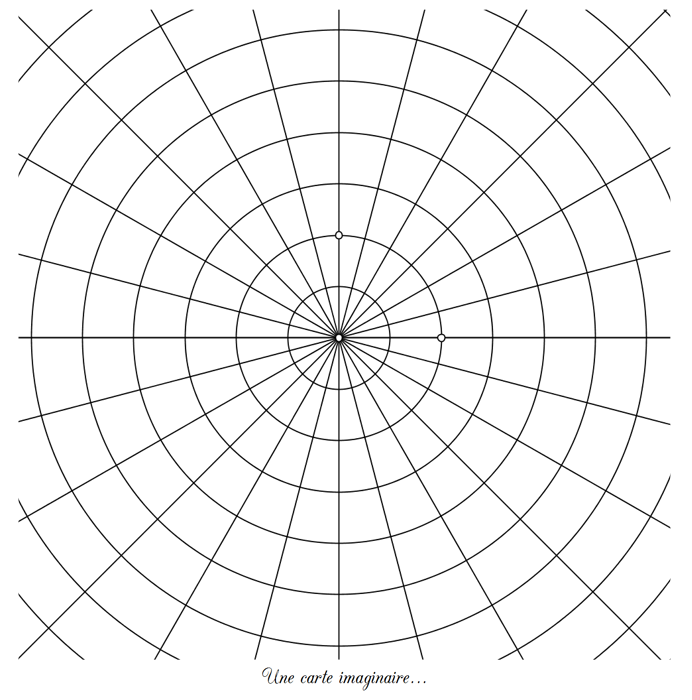
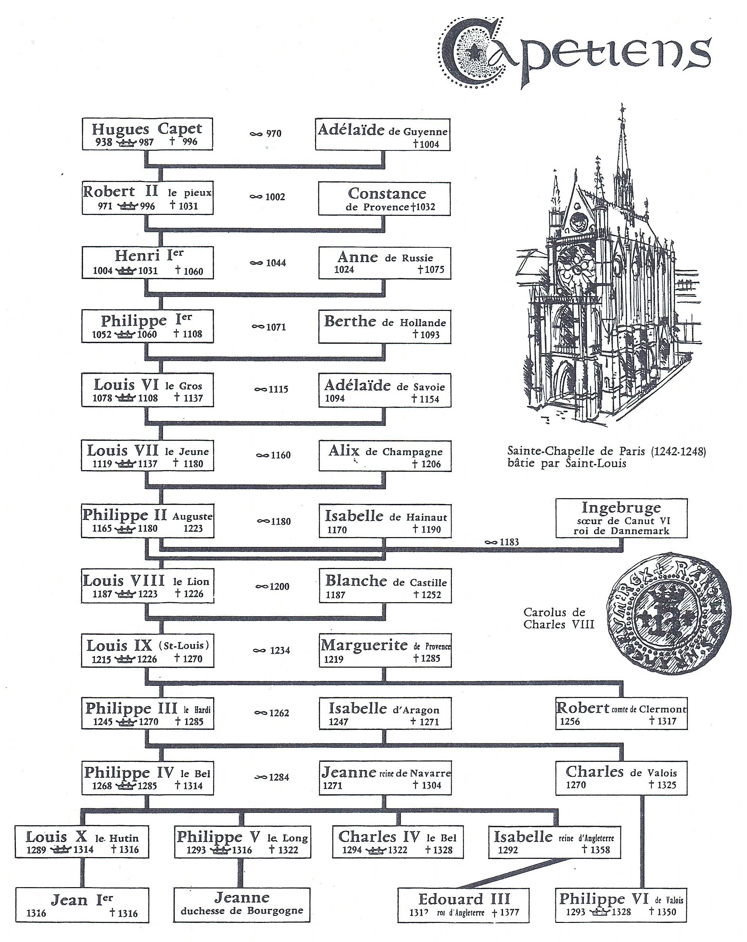
Il suffit alors de placer l’origine du repère sur Macon puis le point blanc de l’axe réel sur St-Louis. On peut ensuite lire l’affixe de Montpelier puis celle de Grand Forks (les «grandes fourchettes» de l’énigme). On trouve respectivement \(2\,\mathrm{e}^{-\mathrm{i}\,\textstyle\frac{5\pi}{12}}\) et \(2,5\,\mathrm{e}^{-\mathrm{i}\,\textstyle\frac{\pi}{12}}\).

Le code du cadenas noir est alors donné par le calcul suivant : \(\left(\dfrac{2\,\mathrm{e}^{-\mathrm{i}\,\textstyle\frac{5\pi}{12}}}{\dfrac{1}{5}\times 2,5\,\mathrm{e}^{-\mathrm{i}\,\textstyle\frac{\pi}{12}}}\right)^{6}=4096\).

La grille est en fait légèrement irrégulière pour que les villes tombent parfaitement sur les nœuds du quadrillage mais cela passe inaperçu.

Troisième énigme : autour des suites

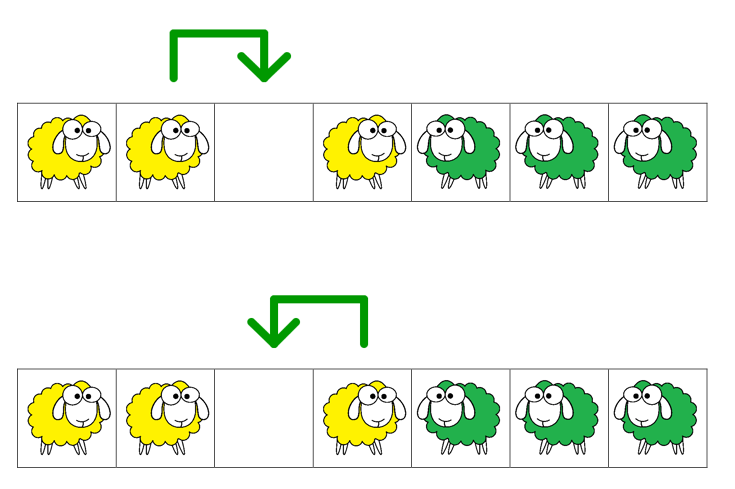
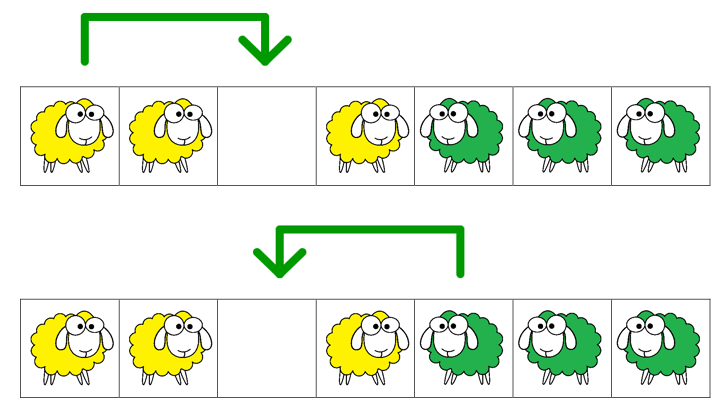
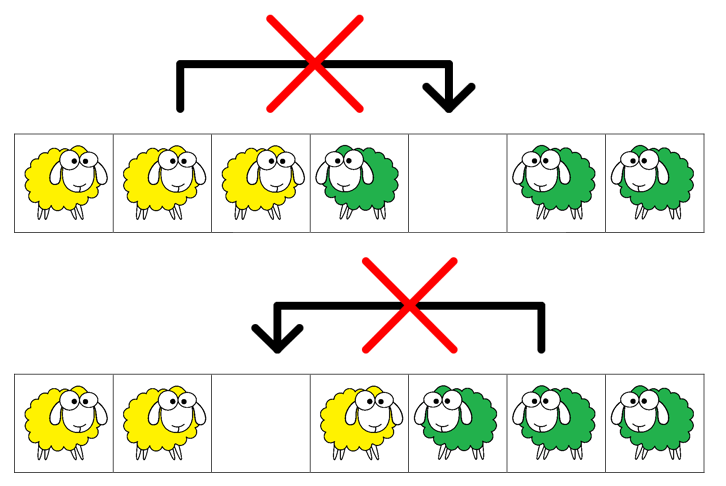
Le regroupement des documents nécessaires à la résolution de cette troisième énigme se fait très rapidement. Trois dessins donnent les règles du jeu :

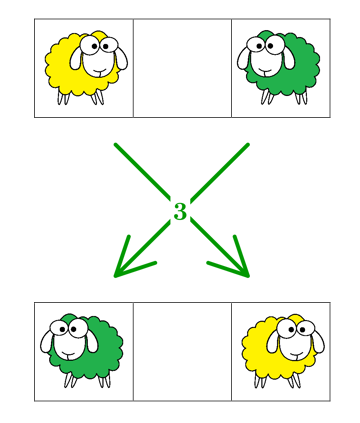
Deux autres donnent le résultat obtenu dans des cas simples :

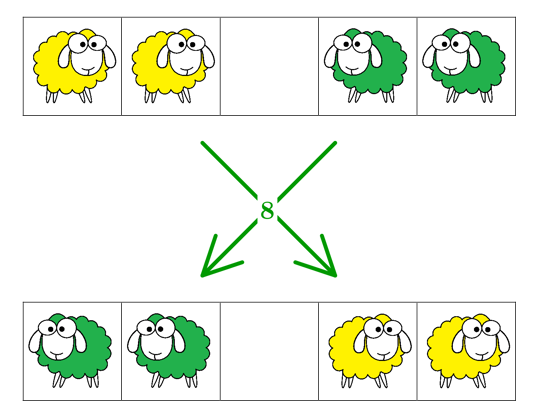
Les élèves disposent également d’une version du jeu en bois avec quatre pions jaunes et quatre pions verts.

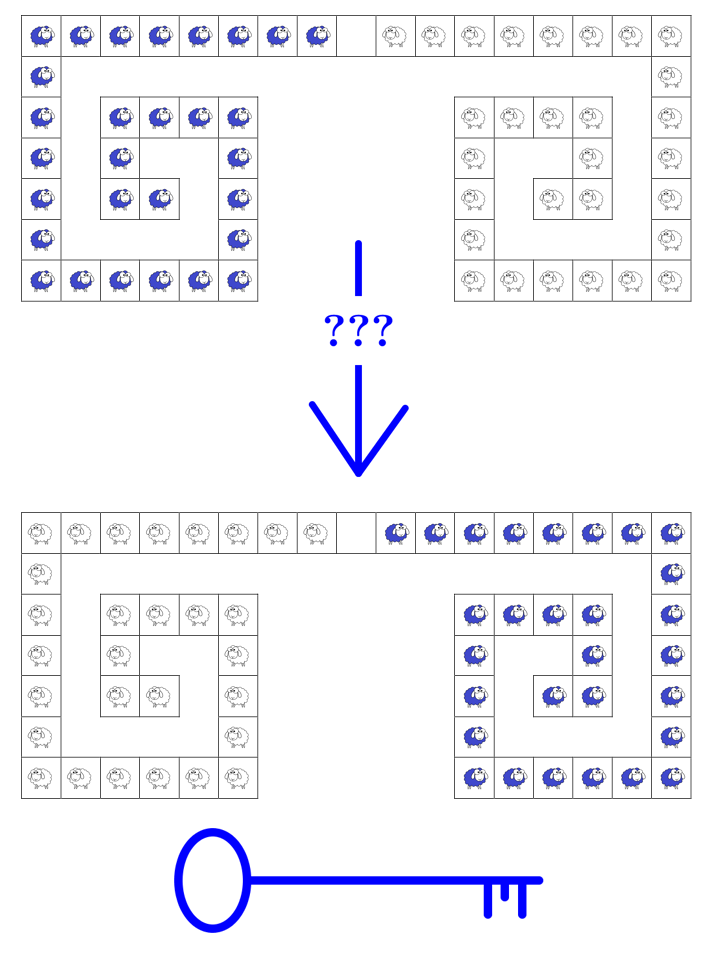
Le but est d’échanger les moutons de chaque couleur en respectant les règles suivantes : un mouton peut aller sur une case voisine ou sauter par-dessus un congénère mais pas plus.

Lorsqu’il y a un mouton de chaque côté du plateau de jeu, il faut au moins \(3\) mouvements (le jaune avance d’un pas, le vert passe par-dessus, le jaune avance encore d’un pas).

Lorsqu’il y a deux moutons de chaque côté, il faut au moins \(8\) mouvements.

L’énigme consiste à trouver combien il faut de mouvements au minimum pour \(29\) moutons.

Les élèves peuvent expérimenter sur de petites valeurs (jusqu’à \(4\) moutons de chaque côté par exemple). En notant \(u_{n}\) le nombre minimum de mouvements nécessaires pour réussir le jeu avec \(n\) moutons de chaque côté, on trouve alors : \(u_{1}=3\), \(u_{2} = 8\), \(u_{3}= 15\), \(u_{4}=24\), etc. On peut ainsi conjecturer une formule directe en fonction du nombre \(n\) de moutons (à savoir : \((n+1)^{2}-1\)) ou une relation de récurrence (sans qu’une justification ne soit nécessairement attendue). Le code bleu est finalement égal à \(30^{2}-1\), soit \(899\).

Les approches pour trouver le résultat sont diverses selon le raisonnement suivi, même sans outil numérique (la calculatrice est interdite pour le jeu, et le recours à l’ordinateur aussi !). Certains élèves remarquent par exemple que \(u_{2}=u_{1}+5\), \(u_{3}=u_{2}+7\), \(u_{4}=u_{3}+9\), et calculent finalement une somme de termes d’une suite arithmétique. D’autres remarquent que \(u_{n}=n(n+2)\).

Quatrième énigme : géométrie dans l’espace

Les élèves disposent cette fois-ci d’un patron et d’un texte donnés ci-dessous.

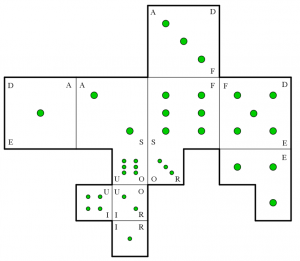
Pour résoudre cette énigme, il faut commencer par assembler le patron (on peut en prévoir plusieurs exemplaires). On obtient alors un assemblage de deux dés cubiques positionnés l’un sur l’autre. Comme indiqué dans le texte, on se place ensuite dans le repère \(\left(\mathrm{O}\,;\,\overrightarrow{\mathrm{OR}},\ \overrightarrow{\mathrm{OU}},\ \overrightarrow{\mathrm{OS}}\right)\).

Dans ce repère, le plan \(\mathcal{P}\) orthogonal à la droite \((\mathrm{ID})\) passant par \(\mathrm{D}\) a pour équation cartésienne : \[x+y+3z-13=0\] La droite \((\mathrm{EU})\), intersection des plans \((\mathrm{EAU})\) et \((\mathrm{FEU})\) a pour représentation paramétrique : \[\left\{\begin{array}{l} x=2+2t\\ y=2+t \\ z=1+t\\ \end{array} \right.,\ t \in \mathbb{R}\] Le point d’intersection de \(\mathcal{P}\) et \((\mathrm{EU})\) a pour coordonnées \(\left(4\,;\,3\,;\,2\right)\) ce qui donne le code du cadenas vert.

Cinquième énigme : probabilités

Pour ce dernier problème, les élèves disposent d’une enveloppe sur laquelle il est écrit « test » en rouge et qui contient un puzzle de \(24\) pièces de la table de la loi normale centrée réduite. Ils disposent également de l’article ci-dessous.

On note \(X\) la variable aléatoire égale au temps mis par les cobayes pour résoudre le puzzle.

La résolution de l’énigme demande de faire quelques hypothèses qui viennent assez naturellement : on peut penser que \(X\) suit une loi normale de moyenne \(\mu=300\) et d’écart-type \(\sigma\).

L’article indique que \(P(289 \leqslant X \leqslant 311)=0,34\). On en déduit que \(P\left(\dfrac{X-300}{\sigma}\leqslant\dfrac{11}{\sigma}\right)=0,67\). La lecture de la table de loi normale centrée réduite donne alors \(\sigma=25\).

On cherche la donnée \(x\) barrée d’un trait rouge et qui constitue le code du dernier cadenas. On a \(P(X \geqslant x)=0,025\) donc \(P\left(\dfrac{X-300}{25}\leqslant\dfrac{x-300}{25}\right)=0,975\). La table donne alors \(\dfrac{x-300}{25}=1,96\) et on a donc \(x=349\).

Bilan de l’activité

Cette activité a été testée sur trois groupes d’élèves de terminale S : deux demi-groupes de 18 élèves issus d’une même classe et un groupe de 12 élèves issu d’une autre classe. Les deux groupes de 18 élèves ont pu se délecter des bonbons cachés dans la valisette dans le temps imparti (en terminant la résolution des cinq énigmes respectivement trois et cinq minutes avant la sonnerie). Le groupe de 12 élèves a mis environ une heure et demie pour résoudre l’ensemble des problèmes. Les deux demi-groupes issus de la même classe étaient mis en concurrence en étant chronométrés, ajoutant ainsi encore un peu plus de piment au jeu.

Tous les élèves se sont fortement impliqués dans l’activité proposée. Ils ont travaillé dans l’enthousiasme et la bonne humeur, y compris quand ils se sont rendu compte que les thèmes sur lesquels ils se retrouvaient à réfléchir n’étaient pas ceux qu’ils préféraient (« Ah ! Mais il faut se servir des nombres complexes en fait ! »)

La plupart des grands thèmes du programme de terminale S ont été abordés dans ce jeu et interdire l’usage de la calculatrice s’est souvent avéré source de discussions intéressantes sur la façon de mener certains calculs efficacement. Par exemple, lors de la résolution de l’énigme de probabilités, les élèves sont amenés à calculer le quotient \(\dfrac{11}{0,44}\) ou le produit \(1,96\times 25\). Poser ces opérations à la main peut s’avérer laborieux, même en terminale ! Constater qu’avec un peu de réflexion ils peuvent y arriver de tête sans rien écrire est pour nombre d’entre eux une redécouverte pleine d’émerveillement.

Évidemment, toutes les compétences attendues pour réussir à l’examen ne sont pas travaillées, en particulier la communication par écrit, mais sortir ainsi des sentiers battus permet aussi de prendre un peu de recul sur les enchaînements de questions classiques des énoncés d’annales. Tous les documents étant mélangés au départ, les groupes d’élèves se sont formés de façon aléatoire. Cela les a aussi obligés, au moins dans un premier temps, à communiquer oralement de façon assez précise.

Il va de soi que toutes les énigmes ne sont pas traitées par tous les élèves mais elles peuvent être exploitées à nouveau lors des séances suivantes car chacun est curieux de comprendre comment a été résolue l’énigme du groupe voisin, notamment celles qui nécessitaient une manipulation (le puzzle en probabilités, le casse-tête avec les moutons, la carte des États-Unis ou encore le patron en géométrie).

Le concept global du jeu peut être adapté à d’autres programmes, à d’autres niveaux et à d’autres moments de l’année. Il suffit pour cela d’imaginer de nouvelles énigmes ! Plastifier les documents permet également de les réutiliser plusieurs fois sans souci.

Voilà en tout cas de quoi apporter un peu plus de gaieté aux dernières séances de l’année et rompre la monotonie des sempiternels exercices «type bac» !

Je tiens à remercier Claire Aoustin pour son soutien logistique et son envie communicative de réaliser ce type d’activités ainsi que Thierry Lesage et Frédéric Gantois, mes collègues cobayes, dont les remarques ont permis d’améliorer ce jeu avant sa mise en œuvre en classe !

Tous les documents sont disponibles ici .

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Fabien Aoustin a expérimenté l’activité présentée dans cet article au lycée Condorcet de Saint-Quentin. Il est désormais en poste au lycée Paul Guérin de Niort et collabore régulièrement au magazine Tangente.