Les Sixièmes ne manquent pas d’aire !

Voici deux jolies activités destinées à consolider la notion d’aire et à différencier les notions de périmètre et d’aire en 6^e. Issues de Bulletins inter-IREM [1], elles ont été adaptées au fur et à mesure des années, des élèves et des programmes, et présentées lors d’un stage PAF animé par le groupe MONAF¹ de l’IREM de Rouen.

Anne Dusson & Nathalie Lecouturier

© APMEP Septembre 2019

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Ces deux activités sont complémentaires l’une de l’autre et l’idéal est de les proposer toutes les deux et dans l’ordre donné ci-dessous. En effet, la première est très cadrée du point de vue des manipulations mais elle présente une déstabilisation dans la perception ; elle contribue à une remise en cause des croyances mathématiques et donne une ouverture pour un nouvel apprentissage. La deuxième laisse place à l’imagination dans les manipulations ce qui, d’ailleurs, peut être déstabilisant pour certains élèves. Dans tout l’article, nous désignerons par tangram l’ensemble des sept pièces du célèbre jeu.

Figure 1. Tangram. ↩

1 ^re activité : tangram et bateau

L’objectif principal est de consolider la notion d’aire en apprenant à aiguiser l’œil du mathématicien qui doit s’habituer à se méfier de ce qu’il voit et deviner ce qu’il ne voit pas.

Étape n°1 : la problématique

Dans un premier temps, aucun matériel n’est distribué de façon à focaliser l’attention des élèves sur la problématique posée. On montre au vidéoprojecteur (ou rétroprojecteur) trois figures en même temps et on pose la question : « À votre avis, ces figures ont-elles la même aire ? Et si vous pensez que non, quelle est celle qui a la plus grande aire ? »

Il est parfois nécessaire d’expliciter ce qu’on appelle « l’aire des figures ». On parle alors de la place occupée par chaque figure au tableau ou sur la feuille en donnant l’image d’une surface qu’on aurait à peindre ou à colorier. On précise également qu’on donne un avis sur un ressenti ou une impression que l’on a, sans être sûr de la réalité.

Figure 2. Les trois figures. ↩

Chacun va donner son avis et, pour récolter les réponses, on convient de donner des noms aux trois figures : le rectangle, le carré et le bateau. Les résultats du sondage sont écrits au fur et à mesure au tableau.

Majoritairement les élèves pensent que le bateau a la plus grande aire et le carré la plus petite. Les avis sont beaucoup plus partagés entre le carré et le rectangle et certains élèves pensent qu’ils ont la même aire.

Ce sondage terminé, on fait remarquer à la classe que les perceptions sont différentes selon les élèves et on leur propose une méthode qui va permettre de prouver ce que l’on affirme et ainsi se mettre d’accord.

Étape 2 : Un moyen pour prouver

C’est là que l’on introduit le tangram.

Matériel par élève

• Une feuille avec les trois figures (Figure 2).

• Un tangram (donné sous forme de carré) sur une feuille cartonnée de couleur (Figure 1).

Le tangram carré a les mêmes dimensions que le carré de la feuille précédente. Prévoir des tangrams de couleurs différentes pour des voisins de façon à ne pas mélanger les pièces.

Consignes orales données au fur et à mesure :

1. Découper avec précision les pièces du tangram et, sur la feuille, reconstituer le carré.

2. Sur la feuille, reconstituer le rectangle à l’aide des pièces du tangram. Observer si toutes les pièces sont utilisées.

3. Sur la feuille, reconstituer le bateau à l’aide des pièces du tangram. Observer si toutes les pièces sont utilisées.

Certains élèves ont besoin du modèle d’avant le découpage pour reconstituer le carré et l’aide des pairs est importante pour le rectangle et le bateau mais les élèves sont motivés par ce travail de puzzle abordable par tous.

Une fois cette étape franchie — sachant que le rectangle s’obtient avec les sept pièces du tangram et que le bateau utilise une pièce de moins et offre plusieurs solutions — le débat de classe peut reprendre en ce qui concerne la comparaison des aires des trois figures.

Conclusion

On fait donc émerger le fait que le carré et le rectangle ont la même aire et que le bateau a une aire plus petite. C’est le moment de revenir aux impressions du début. Il paraît important de se méfier de ce que l’on voit. Pour rassurer les élèves qui se sont trompés au début, on peut faire la distinction entre l’aire et l’encombrement, ce dernier relevant plus d’une impression et, par là même, source d’erreur. Puis en repensant aux différences de ressentis, on retiendra l’importance de trouver une méthode qui permettra de prouver et de se mettre d’accord. Comme ces deux derniers points sont transférables à d’autres situations, cette activité est très formatrice pour les jeunes mathématiciens que sont nos élèves.

Dans le cahier

Les élèves collent les pièces du tangram utilisées sur le bateau et mettent à côté la pièce inutilisée comme sur les figures 3 et 4, puis chaque élève écrit ce qu’il retient de ce travail.

Figure 3. Production d’élève. ↩

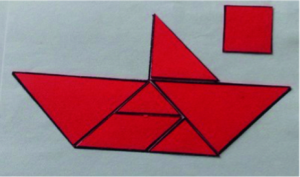
Figure 4. Production d’élève. ↩

2^e activité : les deux rectangles

Objectif principal

Il s’agit de dissocier les concepts d’aire et de périmètre sans avoir recours aux mesures.

Matériel pour chaque élève

• Deux rectangles de même couleur et de mêmes dimensions (en prévoir plus que le nombre d’élèves en raison des erreurs possibles).

• Un tube de colle

• Une paire de ciseaux

Déroulement

Chaque élève reçoit un premier rectangle de couleur et le colle dans son cahier sur la page de gauche.

Puis il reçoit un deuxième rectangle identique (même couleur et mêmes dimensions).

Des élèves voisins ont des rectangles de couleurs et de dimensions différentes pour éviter les mélanges de pièces.

Consignes données au fur et à mesure au vidéoprojecteur :

1. Sur le deuxième rectangle, tracer des segments qui partagent le rectangle en cinq morceaux de forme quelconque.

2. Découper les cinq morceaux.

3. Inventer une nouvelle figure d’un seul tenant en juxtaposant les cinq morceaux.

4. Coller la figure obtenue en dessous du rectangle de départ ou sur la page de droite s’il n’y a pas assez de place.

5. Comparer la figure obtenue et le rectangle de départ : qu’est-ce qui change ? Qu’est-ce qui ne change pas ?

Description et analyse

Pour certains élèves, obtenir cinq morceaux exactement (ni quatre, ni plus de cinq) est difficile. Il faut parfois préciser aux élèves que l’on découpe avec des ciseaux et non en déchirant… L’invention d’une nouvelle figure perturbe des élèves peu habitués à faire travailler leur imagination. En revanche, une fois qu’ils s’autorisent à créer, les élèves laissent libre cours à leur imagination, cherchant à réaliser des figures évoquant un bonhomme, un bateau, etc.

Figure 5. Productions d’élèves.

Pour la comparaison, les élèves commencent par écrire sur leur cahier puis échangent en débat de classe. Ce qui émerge après discussion :

Dans un premier temps, certains disent que l’aire change donc il faut revenir sur la notion d’aire d’une figure et la distinction entre aire et encombrement que l’on fait apparaître dans la première colonne.

Dans un deuxième temps, l’aire rejoint la colonne « Ce qui ne change pas » mais alors, certains élèves pensent qu’il en est de même pour le périmètre.

On revient sur la notion de périmètre et on trouve un moyen de comparer les deux. L’utilisation d’une ficelle est proposée ainsi que la règle graduée et le compas. Selon le temps, ce travail commencé en classe peut être terminé à la maison.

Dans le cahier

Deux figures de formes différentes peuvent avoir la même aire.

Deux figures de même aire n’ont pas nécessairement le même périmètre.

Prolongements possibles

• Le groupe « Jeux2Maths »  de l’IREM de Caen propose deux activités pouvant être utilisées en prolongement :

  • Le jeu Périmaire  est un jeu de cartes (aux motifs constitués de carrés) pouvant se jouer en îlots et ne nécessitant aucune formule. Il s’agit de proposer une carte avec une figure ayant le périmètre et/ou l’aire de la carte proposée par l’un des joueurs.

  • Le jeu Périmexpaire  est un peu plus complexe, car cette fois les formes sont curvilignes mais la règle reste inchangée.

• Dans le même esprit, le jeu Curvica

Bilan sur les deux activités

Ces deux activités permettent de travailler les notions d’aire et de périmètre sans avoir recours à des mesures ou des formules. Ce travail est tout indiqué pour des élèves déjà formatés par l’introduction d’unités et/ou de formules mal assimilées.

À la suite de la première activité, au lieu de faire l’activité des deux rectangles, on pourrait faire le même travail de comparaison de périmètres avec les trois figures de l’activité n°1. Mais, proposer une manipulation qui laisse de la place à l’imagination, permet aux élèves de s’approprier leur figure et certains, ayant compris l’enjeu de la démarche, demandent même à recommencer un découpage pour accentuer encore les différences.

Que demander de plus ?

Référence

1. Gérard Combien et Martine Philippon. Aire et périmètre. le tour de l’aire en collège. . Villeurbanne : IREM de Lyon, 1994. ↩

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Anne Dusson et Nathalie Lecouturier enseignent respectivement à Petit-Quevilly (76) au collège Fernand Léger et à Rouen (76) au collège Barbey d’Aurevilly. Elles sont toutes deux membres du groupe MONAF de l’IREM de Rouen.