Mais qui a tué Alan Turing ?
Dans cet article, Katia Vergnaud et Stéphane Mouez nous font découvrir leur « Cluedo » , qui se présente sous la forme d’une enquête fictive basée sur la vie du mathématicien et logicien Alan Turing. Il se prête à un travail transversal intéressant et stimulant pour les élèves placés dans des situations d’apprentissage inédites.
Stéphane Mouez & Katia Vergnaud
© APMEP Mars 2022
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Ayant l’envie de travailler en équipe français / mathématiques et d’éveiller la curiosité de nos élèves de Seconde, nous sommes toujours à la recherche de nouvelles activités développant la mémorisation et l’autonomie de nos élèves. Chaque année, nous proposons un défi à notre classe commune de Seconde. Cette année, nous avons créé un « Cluedo » qui se présente sous la forme d’une enquête fictive basée sur la vie du mathématicien et logicien Alan Turing. Il se prête à un travail transversal intéressant et stimulant pour les élèves placés dans des situations d’apprentissage inédites. Des exercices de logique et de programmation constituent des liens pertinents avec le programme de mathématiques. Les activités sur la mémoire et la lecture d’un texte, éclairant sur la place des femmes à l’université dans cette première partie du siècle, permettent l’ouverture transdisciplinaire recherchée. D’ailleurs, la réflexion sur la condition féminine est souvent amorcée dans les séquences consacrées à la littérature d’idées, une des entrées du programme de français au lycée. D’autre part, cette activité prend tout son sens dans un travail de groupe où les efforts et les qualités de chacun pourront permettre l’élucidation des énigmes. Mener une enquête par équipe, rechercher un coupable, résoudre des énigmes, tels sont les ingrédients qui nous paraissent adaptés pour surprendre nos élèves et sortir ainsi des sentiers battus.
Le travail en groupe se prête en effet tout naturellement à cette enquête fictive sur la vie d’Alan Turing, que les élèves ont déjà découvert lors d’une séance précédente consacrée à la recherche documentaire et à la hiérarchisation des informations en utilisant des cartes mentales. Les libertés que nous prenons avec l’Histoire n’apportent pas de confusion dans l’esprit des élèves : il est important qu’ils soient conscients que ces écarts avec la réalité participent de la mise en œuvre ludique de l’enquête. Les élèves sont ainsi répartis par groupe de quatre en veillant à l’homogénéité des niveaux ; l’idée étant de stimuler leur réflexion par l’interaction entre pairs mais aussi de favoriser l’entraide afin que les élèves plus en difficulté puissent trouver une place valorisante au sein du groupe. Commence alors une compétition bienveillante puisque la résolution de l’énigme doit se faire dans un temps imparti, tout en tentant de la résoudre le plus rapidement possible. Les élèves doivent donc se répartir les tâches afin de mener leur enquête à terme. Solidarité et entraide sont des qualités essentielles dans la réussite du défi.
Avant de démarrer, nous parcourons l’ensemble du document1 avec les élèves afin qu’ils puissent ensuite élaborer leur stratégie. L’enquête se déroule ensuite sur une heure et demie en plusieurs étapes, chacune d’entre elles permettant la collecte d’un indice.
 Place à l’enquête ! |
Place désormais aux indices donnés, avec à chaque fois un petit retour comportant quelques pistes de solutions et des propositions d’élèves sur ces différents indices.
| Premier indice : à la recherche du lieu du crime |
|---|
| Nous allons vous lire une liste de mots associée à des noms de ville. Faites preuve de mémoire ! a) Écrivez les villes dont vous vous souvenez ; b) Le lieu du crime n’est pas dans cette liste… Déterminez à l’aide de la fiche donnée en annexe le lieu du crime (cherchez l’intrus !). |
Pour le premier indice, nous commençons donc par une liste de lieux à mémoriser ; cette liste n’est lue qu’une seule fois avec obligation de poser le stylo pendant la lecture. Une dizaine de minutes après la lecture, elle est donnée aux élèves avec une ville supplémentaire Wilmslow qui est le lieu du crime (voir figure 1).
| Cambridge | Princeton | |
| Bletchley Park | Varsovie | Berlin |
| Londres | Covent Garden | Birmingham |
| Oxford | Paris | Dublin |
| Sherborne |
Cette première étape se présente comme un défi mémoriel se déclinant donc d’abord dans une phase auditive, puis par une visualisation à l’écrit qui permet aux élèves de confronter leur mémoire à la liste donnée pour identifier la ville intruse.

| Deuxième indice : à la recherche du suspect [1] |
|---|
| Toujours à la recherche du suspect, vous surprenez une conversation. Faites preuve de logique ! On pourra s’aider d’un tableau donné dans l’annexe. Dans cette conversation, une seule personne dit la vérité : |
Pour le deuxième indice, le tableau de vérité qui amène à la découverte du suspect nécessitera souvent des explications complémentaires, c’est un exercice nouveau et important pour les élèves qui continueront des études en informatique.
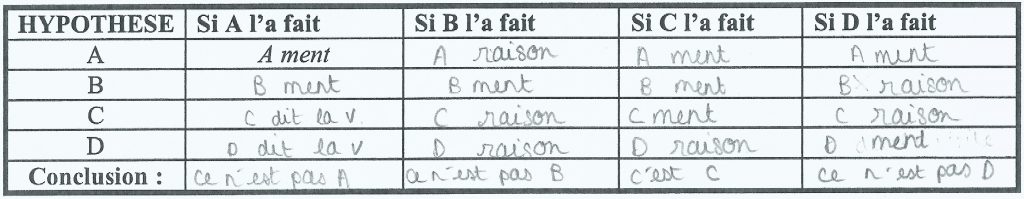
Certains élèves utilisent ici une « approche psychologique » . Par exemple, « C dit juste que ce n’est pas lui, je pense donc qu’il est coupable… » ou bien :

Une méthode par déduction est évidemment possible, méthode que nous donnons aux élèves à la fin de la séance.
Déductions :

| Troisième indice : programmez pour trouver le nombre mystère |
|---|
| Chaque arme porte un numéro, celui recherché correspond à un nombre de Fibonacci. Ce sont des nombres obtenus selon le principe suivant : 1 ; 1 ; \(2=1+1\) ; \(3=1+2\) ; \(5=2+3\) ; \(8=3+5\) ; \(13=5+8\) ; etc.  |
Dans le troisième indice, le numéro de l’arme est un nombre de Fibonacci, l’idée est aussi de poser des jalons portant sur des notions historiques, ici une suite classique. Les élèves doivent alors découvrir ce « nombre mystère » en faisant quelques essais à l’aide du programme proposé dans le texte ; c’est l’occasion d’étudier avec les élèves une boucle « pour » et une suite récurrente d’ordre deux.
| Quatrième indice : à la recherche du mobile |
|---|
Faites preuve d’esprit d’analyse ! • Hugh Alexander (né le 19 avril 1909 à Cork ; mort le 15 février 1974 à Londres) est un cryptanalyste et un joueur d’échecs britannique, né en Irlande. Pendant la Seconde Guerre mondiale, Alexander participa à la cryptanalyse d’Enigma, à Bletchley Park. Après la guerre, il fut pendant vingt ans le chef de la section H (cryptanalyse) du GCHQ ( « Quartier général des communications du gouvernement » ). • En mars 1943, Turing revient à Bletchley Park. En son absence, son adjoint Hugh Alexander avait officiellement pris la fonction de directeur de la Hut 8 2, qu’il avait de fait toujours exercée, Turing n’ayant pas d’intérêt pour la direction. • Après être passée dans un lycée pour filles de Dulwich, Joan Clarke a étudié les mathématiques au Newnham College, une des deux seules universités de Cambridge qui acceptaient les filles. Elle participait aux épreuves de mathématiques, de renommée mondiale, qui exigeaient des plus brillants étudiants de résoudre les problèmes les plus ardus dans un temps imparti. Une expérience précieuse pour sa carrière future. Exceptionnellement douée, elle a été récompensée par le prix Philippa Fawcett, du nom d’une célèbre mathématicienne qui surpassa ses camarades de classe masculins en 1890, et par la bourse Helen Gladstone. En 1939, Joan Clarke fut diplômée avec la mention « double first » (c’est à dire qu’elle était arrivée première à deux de ses examens finaux), mais à titre honorifique seulement puisque Cambridge ne remit de diplôme aux femmes qu’à partir de 1948. • Une course pour décrypter Enigma Arrivée au centre secret de Bletchley Park en juin 1940, Joan Clarke a rejoint la Hut 8 chargée de décrypter Enigma, machine d’encodage utilisée par la marine allemande. Chaque jour passé dans cette cabane de bois, installée sur les terrains d’une somptueuse propriété, était une course contre la montre. Durant le printemps 1941, Alan Turing se rapproche de Joan Clarke, une des rares femmes cryptologues à Bletchley Park. Malgré un amour platonique qui ne dépasse jamais l’amitié, il se fiance avec elle car par devoir social, les parents de Joan lui demandent de se marier. Turing rompt les fiançailles durant l’été après lui avoir révélé son homosexualité. a) Selon vous, quel pourrait être le mobile du crime ? b) Quelle réflexion vous inspire le texte sur la condition des femmes à cette époque ? |
L’idée, dans le quatrième indice, est de faire réfléchir les élèves sur la place des femmes dans les milieux universitaires des années 1950, ceci à travers la lecture d’un texte portant sur Joan Clarke. Ce texte est particulièrement éclairant sur les inégalités touchant les femmes dans les domaines de l’éducation et leur marginalisation dans l’accès au savoir à cette époque. Il sera opportun de le remettre en perspective en cours de français en étudiant différents textes émanant de voix féminines dénonçant leur exclusion du savoir.
| Cinquième indice : une dernière preuve… |
|---|
Décryptez le message ! !  Ici, Turing a utilisé la méthode de cryptage suivante : En complétant le tableau ci-dessus, décryptez le message retrouvé sur le papier que tenait Turing. Pour départager les plus rapides
|
Le message secret du cinquième indice est un codage affine, il sera donc décrypté à l’aide d’un tableau qui permettra de confirmer les découvertes des deuxième et quatrième indices.
Les deux questions subsidiaires ont pour objectif de départager les groupes et surtout d’évoquer le principe du test de Turing connu par certains élèves qui trouvent ici une occasion de mettre en valeur leurs connaissances dans le domaine de l’Intelligence Artificielle. Le dernier message secret est chiffré par un code César, c’est un clin d’œil au conte « Blanche Neige » , particulièrement apprécié par Alan Turing (la lettre A est codée C, la lettre B est codée D, etc.).

Pour décrypter ce message, il suffit de décaler chaque lettre de deux rangs vers la gauche. Il est évidemment possible de donner un coup de pouce aux groupes complètement bloqués.
Les élèves obtiennent ainsi :


Quelques restitutions d’élèves
Voici les résultats d’un premier groupe :

Les résultats d’un second groupe :

Pour conclure ce « Cluedo » , nous proposons une synthèse sous la forme d’un schéma. Ces activités qui fonctionnent très bien, quel que soit le profil de la classe, ont naturellement prolongé de façon ludique l’étude de la vie et des découvertes d’Alan Turing que nous avions pu travailler auparavant.

Références
- [1] Linda V. Williams. Deux cerveaux pour apprendre.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Katia Vergnaud et Stéphane Mouez enseignent respectivement le français et les mathématiques au lycée Alfred Kastler de Talence.
- Vous trouverez ici le sujet entier.
- La Hut 8 était une section du bureau anglais responsable de l’interception et du déchiffrage des communications étrangères entre 1919 et 1946. Elle était chargée de chargée de résoudre les messages Enigma de la marine allemande pendant la seconde guerre mondiale.

2 réflexions sur « Mais qui a tué Alan Turing ? »
Les commentaires sont fermés.