Quelques bricolages pour le cercle trigonométrique

À l’école, au collège, au lycée ou à l’université, l’un des intérêts des objets n’est pas simplement de pouvoir les manipuler mais aussi de s’interroger sur comment ils fonctionnent et ensuite pourquoi ils fonctionnent. Olivier Longuet nous propose dans ce cadre quelques objets à utiliser avec nos classes dans le secondaire. Des ciseaux, du carton, de la colle, un peu d’imagination pour rendre les mathématiques vivantes.

Olivier Longuet

© APMEP Mars 2019

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Dans mes cours, j’aime beaucoup proposer des approches différentes pour introduire des notions ou des formules. En plus d’activités classiques, je présente dès que je le peux des objets qui, par leur manipulation, vont permettre aux élèves de mieux comprendre les concepts étudiés. J’y vois plusieurs avantages, notamment d’éveiller l’intérêt des élèves, de les aider à mémoriser les résultats, d’offrir à certains élèves plus kinesthésiques d’autres entrées moins abstraites. Dans un premier temps, l’objet présenté les amuse, puis les questions arrivent : «comment ça marche ?», «pourquoi ça marche ?» favorisant ensuite le débat et l’introduction de la notion mathématique.

Pourquoi des objets manipulables ?

Le matériel de manipulation aide les élèves à passer du concret à l’abstrait ; manipuler permet de mettre plus facilement les raisonnements à l’épreuve, de reconnaître des régularités, des relations, de construire des images mentales.

Les élèves se souviennent généralement bien des objets, ce qui en fait un point d’ancrage. Au moment où on a besoin de réactiver une notion, on peut ressortir l’objet qui a servi à l’introduire et les problématiques évoquées reviennent facilement aux élèves. Mieux, si on assure ses cours dans une seule salle, on peut les accrocher au mur et s’en servir à l’occasion.

Objet, mode d’emploi

L’arrivée d’un nouvel objet dans la classe commence par une phase de découverte. Je le manipule devant eux. Parfois, j’annonce le rôle de l’objet et je le place dans une certaine position. Je demande ensuite de justifier que l’objet donne la réponse que j’attends.

S’ensuit la phase de débat, où le passage de l’univers du manipulable à celui des figures géométriques est nécessaire pour verbaliser.

Je déplore que les élèves n’aient pas systématiquement le réflexe de réaliser un schéma, une figure codée pour réfléchir. Souvent, elle est donnée dans l’énoncé d’un problème et n’est pas reproduite sur le cahier.

Le fait de dessiner puis de simplifier l’objet est une phase importante, où le travail d’abstraction s’effectue en cherchant quels sont les liens entre les différentes composantes de l’objet et ce que cela implique au sens géométrique (égalité de longueur, droites perpendiculaires, etc).

Je pourrais bien entendu utiliser les logiciels de géométrie dynamique, mais je me suis aperçu que lorsque j’utilise la souris, je suis concentré sur l’écran et je ne regarde pas les élèves.

Or, regarder ses élèves est important quand on veut animer le débat dans la classe. Aussi, si j’utilise souvent l’outil informatique, c’est plutôt au moment de la conclusion, lors de la phase de verbalisation finale, comme autre moyen de visualisation et comme confirmation des définitions ou propriétés que je voulais travailler.

Objet n° 1

L’objectif de cet objet est de distinguer la notion d’angle et de cosinus, beaucoup d’élèves faisant souvent la confusion entre les deux. Il peut être présenté dès le cycle 4 pour présenter le cosinus d’un angle aigu. Il consiste en un bras articulé autour d’un axe, de longueur une unité, au bout duquel on attache un fil à plomb.

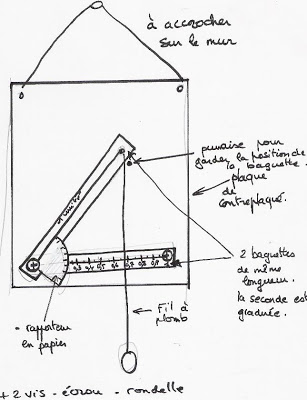
En tenant l’objet verticalement, le fil à plomb permet de visualiser le projeté orthogonal du point sur le côté adjacent. On remarque que le quart de cercle n’est pas tracé, la question en quatrième étant surtout l’étude des triangles rectangles. Cela dit, au bout de quelques années d’utilisation, le cercle se dessine avec l’usure de l’objet.

L’élève peut manipuler l’objet lors d’un exercice où il doit estimer le cosinus d’un angle donné, ou la mesure d’un angle dont on connaît le cosinus. Il peut ensuite vérifier et affiner avec la calculatrice.

J’ai récemment utilisé cet objet pour commencer mon cours sur la trigonométrie en seconde en réglant l’angle sur 60° et en remarquant que le résultat obtenu était 0,5 ; pour un angle de 45°, on obtient 0,7. Comment ça marche ? Est-ce que ces résultats sont précis ? S’est alors instauré un débat où certains élèves, peu communicatifs d’habitude, ont été intrigués et ont apporté des remarques intéressantes à la classe : « le fil à plomb est vertical », « on obtient un triangle rectangle », « l’hypoténuse a pour longueur 1 », « on peut utiliser SOHCAHTOA ».

En amenant le questionnement à partir d’un objet concret, le cadre a changé par rapport à un questionnement sur papier, j’ai interpellé certains élèves plus bricoleurs, plus kinesthésiques. J’ai ouvert des portes supplémentaires pour aborder la notion. Sans doute d’autres élèves avec un rapport plus classique à l’écrit ont-ils été troublés. Ils retrouveront leurs marques un peu plus tard.

Objet n° 2

L’objet présenté maintenant a pour but de visualiser des cosinus et des sinus d’angles quelconques. Ici, le cercle est tracé explicitement, les angles remarquables sont indiqués en radians sur le cercle rouge, rappelant ainsi l’enroulement de la droite autour du cercle. Au bout du bras articulé, sur le même principe, un fil à plomb, qui va permettre de projeter orthogonalement sur l’axe des cosinus, pour un angle compris entre \(0\) et \(2\pi\).

Ce dispositif a des défauts, notamment celui de ne pas permettre la lecture des sinus, mais il a l’avantage d’être simple et facilement compréhensible en première approche. François Bouyer a proposé l’objet 2bis suivant, il sera testé prochainement.

Objet 2bis:

Pour lire cette fois les sinus d’un angle donné ainsi que les cosinus des angles compris entre \(\pi\) et \(2\pi\), il va falloir un peu plus qu’un fil à plomb. On fait un trou au centre d’une plaque de plexiglas, on trace deux droites perpendiculaires sécantes en ce trou. On leste cette plaque sur une de ses verticales, avec un lest d’environ 200 grammes.

Cet objet, plus fragile que le précédent, demande à être manipulé avec précaution. Il est particulièrement intéressant pour aborder les mesures principales d’un angle en radian, le signe d’un cosinus et d’un sinus d’un angle donné et surtout les variations de ces deux fonctions, ou encore pour résoudre des équations trigonométriques.

Objet n° 3

Cet objet reprend une idée de Gérald Giangrande, un collègue animateur de l’IREM de Caen très inventif. Il aime fabriquer des objets mathématiques avec une finition travaillée qui donnent des résultats précis, pour lesquels la compréhension du fonctionnement n’est pas évidente a priori et demande une vraie réflexion.

On superpose les trois couches de cartons pour permettre au point mobile (bouton de jean surmonté d’un piton à vis) de circuler sur un rail. L’idée est d’utiliser un cercle de diamètre 1, tournant autour de l’origine du repère.

Cet objet utilise le théorème du cercle circonscrit à un triangle rectangle. Soit \(\mathsf{H}\) le deuxième point d’intersection du petit cercle avec l’axe des abscisses. Le point \(\mathsf{H}\) appartient au cercle de diamètre \([\mathsf{OM}]\), donc le triangle \(\mathsf{OMH}\) est rectangle en \(\mathsf{H}\). Comme \(\mathsf{H}\) appartient à l’axe des abscisses, le point \(\mathsf{H}\) est le projeté orthogonal de \(\mathsf{M}\) sur l’axe des abscisses. On peut donc lire le cosinus de l’angle \(\widehat{\mathsf{IOM}}\). Cet objet est un théorème en action, qui permet une lecture de mesures.

J’aime particulièrement l’idée de l’objet, même si la lecture du sens de variation des fonctions est beaucoup moins intuitive : il y a un obstacle, il faut oublier qu’on visualise l’intersection d’un cercle et d’une droite, il faut se dire sans cesse qu’on a le projeté orthogonal donnant le cosinus et le sinus. Cela fait beaucoup d’opérations mentales, la lecture est moins directe, certains élèves peuvent décrocher en se demandant ce qu’on visualise.

Cela dit, c’est peut être ce qui rend cet objet si intéressant : il est intrigant, il ne se laisse dévoiler qu’après une certaine réflexion. Lorsqu’on a compris, on est très content : aha ! comme dirait Martin Gardner, ça chatouille comme une œuvre d’art.

Objet n° 4

À l’aide de cet objet, on peut déterminer le cosinus et le sinus d’un angle aigu donné, ou encore à partir de la valeur d’un cosinus, déterminer la valeur de l’angle aigu et la valeur du sinus. On pourra dessiner le cercle trigonométrique et utiliser les propriétés des angles associés pour trouver les solutions sur le cercle entier.

Gérald Giangrande propose cet objet imposant et un peu mystérieux lors des portes ouvertes de son lycée et dans sa classe. Il est composé d’un demi carré \(\mathsf{OIJ}\) d’un mètre de côté et d’une règle de plexiglas. Sur les deux côtés de l’angle droit de cette équerre isocèle en \(\mathsf{O}\), des mètres rubans ont été collés comme graduation. Un quart de cercle de centre \(\mathsf{O}\) et de rayon \(\dfrac{1}{2}\) a été tracé et gradué en degré. Sur la règle de plexiglas, on a placé deux clous à un mètre de distance, aux points \(\mathsf{M}\) et \(\mathsf{N}\). Le milieu \(\mathsf{K}\) du segment \([\mathsf{MN}]\) est marqué.

On place la règle de manière à ce que les clous touchent les deux côtés de l’angle droit.

Le lieu géométrique du point \(\mathsf{K}\) est le quart de cercle de centre \(\mathsf{O}\) et de rayon \(\dfrac{1}{2}\cdotp\)

On peut lire la mesure de l’angle \(\widehat{\mathsf{IOK}}\), l’abscisse du point \(\mathsf{M}\) et l’ordonnée du point \(\mathsf{N}\).

On a alors \(\cos \left(\widehat{\mathsf{IOK}}\right) = x_{\mathsf{M}}\) et \(\sin \left(\widehat{\mathsf{IOK}}\right)= y_{\mathsf{N}}\).

En pratique, les valeurs sont assez précises à \(1\) ou \(2\) millièmes près.

L’explication du fonctionnement de cet objet n’est pas immédiate : on ne voit plus du tout le projeté orthogonal d’un point du cercle. Pour mieux comprendre, on peut considérer le point \(\mathsf{O}’\), symétrique de \(\mathsf{O}\) par rapport à \(\mathsf{K}\). Il devient alors facile de justifier que le quadrilatère \(\mathsf{OMO’N}\) est un rectangle et que \(\mathsf{O}’\) appartient au cercle de rayon \(1\).

Sans cette réflexion, le résultat donné par l’instrument paraît un peu magique, la recherche du « truc » peut être motivante pour l’élève, et peut donner lieu à une réflexion collégiale ou à un devoir guidé fait à la maison.

Conclusion

Bon, on peut me dire, maintenant qu’il y a les animations sur GeoGebra tellement plus propres, pourquoi se casser les pieds avec ces manipulations parfois saugrenues ? Eh bien, c’est beaucoup plus fort pour les élèves. GeoGebra est un outil sophistiqué, donnant des images magnifiques, fines et précises. Mais c’est un peu une boîte noire, il fabrique les images, on lui fait confiance.

Que deux bouts de cartons et une ficelle mettent en évidence le même phénomène donne des séquences très vivantes, très parlantes et mémorables pour les élèves ! Les moments où on tient l’objet devant soi, pour présenter les notions ou, plus tard, pour interroger un élève sur les valeurs remarquables ou les variations sont des moments percutants où on fait corps avec les notions.

Des collègues trouveront sûrement des méthodes plus élégantes et fabriqueront des objets plus beaux, plus artistiques mais j’aime assez l’idée qu’on puisse fabriquer des objets intéressants avec des moyens rudimentaires. Cela étant, depuis quelque temps, je fabrique de nombreux objets avec une découpeuse laser dans un fablab, l’objet réalisé est mieux fini.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Olivier Longuet enseigne les mathématiques au lycée Alain Chartier de Bayeux. Il est membre de l’équipe de rédaction d’Au fil des maths et notamment l’auteur de certaines des illustrations.
Lire à son sujet l’article paru dans le Café pédagogique et n’hésitez pas à parcourir son blog.