À la poursuite des flexagones

Voilà la suite de l’article sur les flexagones paru dans le n° 532 d’Au fil des maths.

Loïc Terrier

© APMEP Mars 2020

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Résumé de l’épisode précédent

Dans l’article précédent (Au fil des maths \(532\) ), nous avons découvert les (hexa)flexagones, ces assemblages de triangles qui ressemblent à des hexagones mais cachent en leur sein des faces que l’on révèle par « flexage ». Nous avons constaté qu’il existe (à symétrie près) un seul modèle de flexagone ayant trois, quatre ou cinq faces, mais que les choses semblent se diversifier pour six faces. Il existe en effet plusieurs façons de découper un hexagone en triangles, et on obtient ainsi différents « plans » pour les flexagones à six faces.

Nous avons également vu comment fusionner deux flexagones pour en obtenir un plus grand, et nous allons mettre en pratique cette méthode pour obtenir les patrons des trois flexagones à six faces. Nous verrons un peu plus loin une méthode différente, qui permet, avec un peu de travail, d’obtenir le patron d’un flexagone quelconque à \(n\) faces à partir de son plan.

Avant d’aller plus loin, remarquons qu’un tiers de patron nous suffit pour avoir le patron tout entier : en effet, tout patron de flexagone est constitué de trois tiers identiques. D’autre part, plutôt que de donner le recto et le verso, il sera plus simple de signaler sur le recto la couleur de la face au verso. Par exemple, pour le flexagone à trois faces :

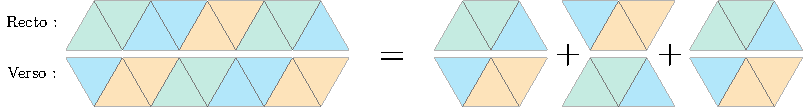
On reprend (sur un tiers seulement) les couleurs du recto et on signale par un trait la couleur au verso. Noter que le trait se situe toujours sur le bord de la bande de papier.

Si on veut reconstituer le patron entier, on met trois tiers bout à bout, en retournant le deuxième tiers (recto/verso) lorsque \(n\) est impair (et uniquement dans ce cas !). Bien sûr quand on retourne un tiers de patron, les couleurs recto et verso s’inversent.

Les trois hexaflexagones

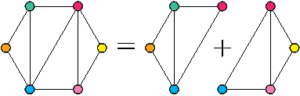
Comme vu dans l’article précédent, on peut fusionner un flexagone à \(n\) faces et un flexagone à \(p\) faces pour obtenir un flexagone à \(n+p-2\) faces. Cette fusion peut se visualiser grâce au plan ou à la carte : sur le plan ce sont deux arêtes qui fusionnent ; sur la carte ce sont deux sommets.

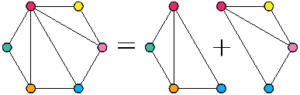
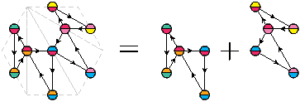
On peut décomposer ce flexagone à six faces en deux flexagones à quatre faces. On cherche alors les patrons de chacun de ces flexagones à quatre faces, et on s’arrange pour que le dernier triangle du premier patron soit le même que le premier triangle du deuxième patron, à savoir le triangle qui va disparaître lors de la fusion (ici on voit qu’il s’agit du triangle rouge/bleu).

Les triangles hachurés sont ceux qu’on coupe lors de la fusion « physique » des flexagones de papier. On obtient le tiers de patron du flexagone à six faces cherché. Reconstituons le patron tout entier pour voir la forme de la bande de papier à utiliser :

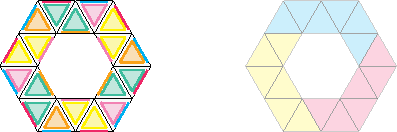
Quelques remarques :

• La forme du patron complet est intéressante en soi : nous l’appelerons silhouette du flexagone. C’est le patron mais sans indication de couleurs. Pour distinguer les trois tiers de patrons, nous utiliserons simplement les trois couleurs primaires : bleu, rouge, jaune. L’intérêt de ce choix apparaîtra plus loin !

• Cette méthode de fusion n’est pas (du tout) une méthode pratique d’obtention du patron ! Elle est présentée ici plutôt comme un moyen de mieux comprendre les mécanismes de la carte et du plan. Nous verrons avec les flexagones à sept faces une méthode très générale et beaucoup plus simple à mettre en œuvre.

• Sur le patron complet, on peut vérifier que les traits indiquant la couleur du verso sont bien au bord de la bande de papier : cela permet de voir comment on recolle les trois tiers et aussi, dans d’autres cas, où découper le papier !

Le deuxième flexagone à six faces peut lui aussi être obtenu en fusionnant deux flexagones à quatre faces.

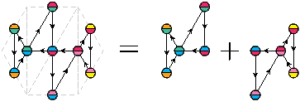
Comme on l’a dit précédemment, les traits indiquant les couleurs des faces au verso sont au bord de la bande de papier : les deux triangles en haut de l’hexagone ne se touchent donc pas : dans la pratique, il faut inciser la feuille. Sur la figure ci-dessous, on a exagéré cette incision pour aider à comprendre que la silhouette de ce flexagone est elle aussi un anneau.

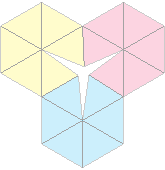
La vidéo ci-dessous montre la création du patron.

Pour le troisième de ces flexagones à six faces, on voit sur le plan qu’on ne peut pas faire autrement que fusionner un flexagone à cinq faces avec un flexagone à trois faces.

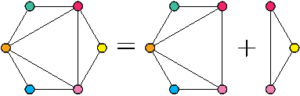
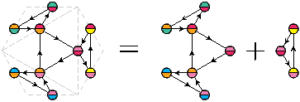
On obtient une silhouette rectiligne¹ : il s’agit du deuxième flexagone historiquement découvert par Arthur Stone, celui-là même qui a sucité l’engouement du « comité de Princeton » ! Très pratique à réaliser pour vos faire-parts !

Une face, six configurations

Lorsque l’on flexe, les triangles constituant la face que l’on a devant soi semblent se mélanger de façon étrange… En réalité, trois morceaux de cette face vont subir des rotations dans l’espace. Les axes de ces rotations sont représentés sur la première figure ci-dessous. La face est maintenant située sous la flexagone : la deuxième figure représente cette face « vue par transparence ». La troisième figure est le résultat obtenu lorsque l’on retourne le flexagone pour remettre la face vers le haut.

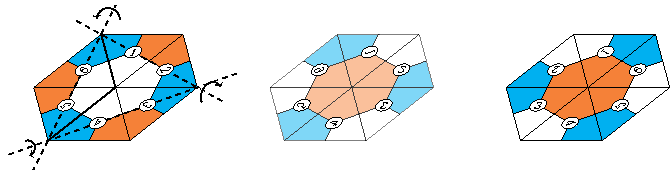
Que se passe-t-il si l’on flexe à nouveau ? Si on utilise les mêmes axes (1-2, 3-4 et 5-6), on revient à la configuration précédente, mais sinon on en obtient une nouvelle. Attention, ce n’est pas toujours possible ! Par exemple avec un flexagone à trois faces, chacune des faces n’est visible que dans deux configurations. Avec des flexagones ayant davantage de faces, celles-ci seront visibles dans trois, quatre, cinq, voire six configurations ! On ne peut pas aller au-delà, car au bout de six fois on est revenu à la configuration initiale :

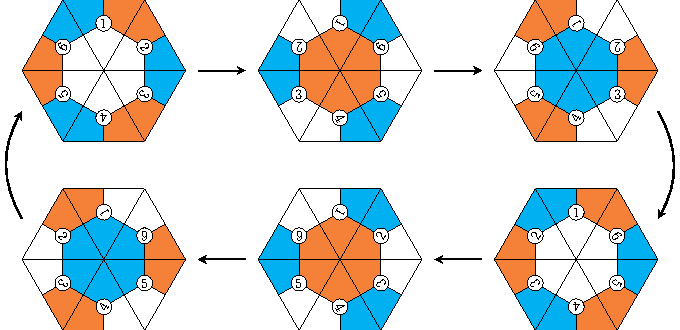
On remarque qu’on bout de trois flexages on a retrouvé le centre initial. Cependant les triangles ne « tournent » pas dans le même sens !

Pour savoir dans combien de configurations une face sera présente, il suffit de regarder le plan. Anticipons un peu et regardons ce plan d’un flexagone à sept faces :

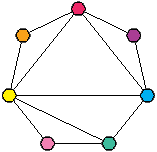
La face rouge, par exemple, est reliée aux faces jaune, orange, violette et bleue. La face rose, quant à elle, n’est reliée qu’aux faces verte et jaune : la face rouge sera présente dans quatre configurations, la face rose seulement dans deux. On peut le vérifier sur la carte : la face rouge apparaît quatre fois, la rose seulement deux fois.

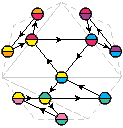
Si on veut que les six configurations soient présentes, il faut qu’un sommet du plan soit relié à six autres sommets. C’est possible pour un flexagone à sept faces, mais pas celui-ci.

L’un des intérêts des flexagones est d’ordre artistique : si l’on dessine sur une face dans une configuration donnée, après flexage les triangles ont été « mélangés » et l’image n’est plus la même.

Question : est-il possible de paver une face de flexagone de sorte que les six configurations soient différentes ? Avec un type de tuile ? Deux ?

Je n’ai pas la réponse à cette question : si vous trouvez de tels pavages, n’hésitez pas à m’envoyer un courriel !

Heptaflexagones

Nous allons maintenant voir une méthode qui permet, à partir du plan d’un flexagone, de déterminer son patron. C’est une variante de la méthode présentée dans la « bible » flexagonale de A. Conrad et D.K. Hartline [1].

Il existe quatre triangulations différentes de l’heptagone :

On peut se demander comment on sait qu’il n’y en a que quatre et aussi comment on les trouve. Une première méthode consiste à rajouter un triangle sur chacun des côtés dans les différentes triangulations de l’hexagone. Il reste ensuite à éliminer les doublons (rotations, symétries). Nous discuterons du cas général dans le paragraphe suivant.

Nous allons déterminer le patron du quatrième flexagone, par exemple. On oublie provisoirement les couleurs des sommets et on procède comme suit :

• on colorie les triangles avec deux couleurs (ici bleu et blanc) de sorte que deux triangles voisins ne soient pas de la même couleur (une récurrence montre que c’est toujours possible) ;

• on marque les milieux de chaque arête, et on relie ces milieux ;

• on numérote les milieux des côtés (extérieurs), consécutivement (dans un sens ou dans l’autre, ça n’a pas d’importance)

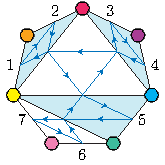
• on ajoute des flèches : dans les triangles en bleu (par exemple) on tourne dans le sens horaire, dans les triangles en blanc dans le sens trigonométrique.

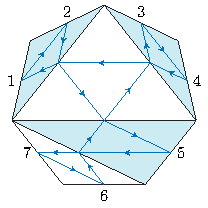
Si vous avez des triangles bleus à la place des blancs (et donc si vos flèches vont dans l’autre sens), ça n’a pas d’importance, car on travaille à symétrie près : on ne fait pas de distinction entre un flexagone et son enantiomère².

Partant du numéro \(1\), on suit les flèches jusqu’à ce qu’on atteigne un autre numéro : dans notre exemple, on arrive à \(2\). Repartant du \(2\), on suit les flèches avec la règle suivante : à chaque « carrefour », on suit la flèche « en face », c’est-à-dire celle qui continue dans le triangle voisin. Du \(2\) on arrive alors au \(5\), puis \(7\) et on poursuit ainsi jusqu’à revenir à \(1\). On note la séquence obtenue : \(1,2,5,7,6,3,4\).

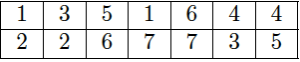
On construit alors un petit tableau en notant les numéros de la séquence alternativement sur la première et sur la deuxième ligne ; on note la couleur du triangle sur la troisième :

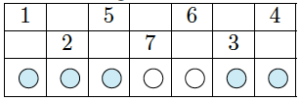
On remplit alors les cases vides de ce triangle : si la colonne contient le numéro \(i\), on y place \(i+1\) (si c’est \(7\), on place \(1\)).

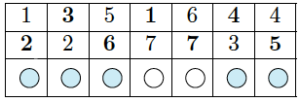
On va, dans un premier temps, déterminer la silhouette du patron, et on complétera ensuite avec les couleurs recto et verso.

Pour la silhouette, on se sert uniquement de la troisième ligne. On va utiliser des « tuiles » de deux types :

Pour réaliser la silhouette, on assemble les tuiles bleues et blanches, en respectant l’ordre de la séquence, en les disposant de sorte que les demi-disques aux bord se correspondent.

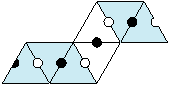
On a alors obtenu le premier tiers, et on peut obtenir la silhouette complète :

Cela peut se faire de deux façons : soit on continue avec les tuiles, en reprenant la séquence au début, soit on assemble les trois tiers directement, sachant que pour un nombre de faces impair on assemble recto + verso + recto.

Maintenant que nous avons la silhouette, il n’y a plus qu’à mettre les couleurs !

On utilise les deux premières lignes du tableau :

On remplace chaque numéro par la couleur qui le précède (en tournant dans le sens croissant des numéros) :

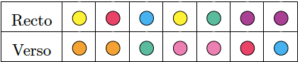
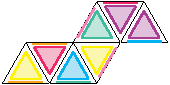
Et voilà ! La méthode est applicable pour tout flexagone… Mais (c’était trop beau) il arrive qu’en construisant la silhouette celle-ci ait le mauvais goût de repasser sur elle-même : c’est le cas par exemple du troisième heptaflexagone dont la silhouette est :

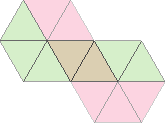
Rappelons que les couleurs utilisées sont, dans l’ordre : bleu, rouge et jaune. Or on voit du rouge, du brun et du vert ! Cela vient du fait qu’on a utilisé de l’opacité : vert résulte de la superposition de bleu et jaune ; brun résulte de la superposition des trois couleurs.

En vidéo :

Autre surprise : deux flexagones différents peuvent avoir la même silhouette ! Leurs patrons seront différents mais la forme générale de la bande de papier utilisée sera la même. Les couleurs conditionnant le pliage du patron, c’est donc celui-ci qui permettra d’obtenir un modèle ou un autre. Ce phénomène apparaît la première fois pour \(n=7\), mais on le retrouve systématiquement par la suite : les flexagones à six faces sont donc en réalité une exception !

Et ensuite ?

Comme promis dans le paragraphe précédent, nous allons discuter du nombre de flexagones à \(n\) faces. Comme vous l’avez compris, il s’agit de compter le nombre de façons de trianguler un polygone régulier à \(n\) côtés, puis d’éliminer les triangulations qui sont identiques à rotations ou symétries près.

Nous n’allons pas entrer dans les détails (cela constituerait un article en soi !) mais donnons les grandes lignes.

• Pour compter les triangulations, on peut établir une bijections entre celles-ci et les « chemins de Dyck », plus faciles à compter. Voir par exemple la jolie vidéo d’El jj [2]. On obtient des nombres de triangulations égaux aux nombres de Catalan.

• Reste à faire le tri pour ne garder qu’un seul représentant par classe d’équivalence : on utilise un résultat de théorie des groupes appelé le « lemme de Burnside » (voir à ce sujet dans l’incontournable livre de J.-P. Delahaye [3] le chapitre qui lui est consacré). On est obligé de distinguer quatre cas, selon les congruences de \(n\) modulo 6 : (\(0\), \(\pm 1\), \(\pm 2\), \(3\)). L’idée générale est expliquée dans un article de Moon et Moser [4].

Après un début timide, le nombre de flexagones croît de façon vertigineuse : \(1\), \(1\), \(1\), \(3\), \(4\), \(12\), \(27\), \(82\), \(228\), \(733\), \(2282\), \(7528\), \(24834\), \(83898\), \(285357\), \(983244\), \(3412420\)…

Vous avez à présent les outils pour vous lancer à votre tour dans l’exploration de l’univers infini des flexagones !

Parmi les rencontres qu’on peut y faire, voici quelques silhouettes :

Jeu : retrouver les tiers de patrons à partir des silhouettes données (précision : on commence toujours par un triangle bleu « pointe en haut »).

Python, Tikz, et les flexagones

Les flexagones fournissent des problèmes algorithmiques à foison : comment générer toutes les triangulations d’un polygone régulier à \(n\) côtés ? Comment reconnaître si deux triangulations sont équivalentes ? Comment générer les patrons, les silhouettes ?

Toutes les figures ont été réalisées à l’aide de scripts Python générant du code Tikz pour LaTeX…

Vous trouverez ci-dessous un script de Pascal Richard (encore merci Pascal !) permettant de créer différents patrons pour quelques modèles de flexagones à partir d’images de votre choix. La procédure est détaillée dans le document notice.

dossier_python

En guise de conclusion

Qu’est-ce qu’un flexagone ? Un bout de papier plié ? La matérialisation d’une triangulation ? Un passe-temps topologique ? Une œuvre d’art en devenir ? Une étrange permutation³ ? Un casse-tête combinatoire ? Un outil pédagogique pour présenter la théorie des groupes⁴ ?

Les flexagones sont tout ça. À mon sens, une porte d’entrée ludique vers de bien belles mathématiques !

Complément

Flexagone à découper.

Références

1. A.S. Conrad et D.K. Hartline. Flexagons. . 1963.↩

2. El Jj. Deux (deux ?) minutes pour. . . les nombres de Catalan. . Youtube. 2017.↩

3. Jean-Paul Delahaye. Pour la science. Mathématiques pour le plaisir. Belin, 2010.↩

4. J. W. Moon et L. Moser. Triangular Dissections of N-Gons. . 1963.↩

5. Leslie Philip Pook. Flexagons Inside Out. Cambridge University Press, 2003.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Loïc Terrier est adhérent de la dynamique régionale de Lorraine. Après avoir sévi de nombreuses années dans le secondaire, il s’en est récemment évadé et tente à présent de convaincre ses élèves de la prépa ECE (classe prépa économique et commerciale, option économique) du lycée Henri Poincaré de Nancy que les mathématiques peuvent être amusantes… Il a animé des ateliers aux Journées Nationales sur \(\LaTeX\), R et les flexagones.

---