Le Kepler Music Project :
un spectacle pour jouer avec les lois de Kepler
Depuis 2012, Le Kepler Music Project1 est un spectacle écrit, composé et interprété par Guy Boistel et Stéphane Le Gars, tous deux chercheurs en histoire des sciences, professeurs de physique-chimie en lycée et musiciens de jazz. Ce spectacle vise à expliquer à tous publics, (grand public, lycéens, chercheurs2, musiciens) et en tous lieux (salles de concert, planétariums, festivals d’astronomie, chapelles, etc.) comment Johannes Kepler a brassé d’importantes considérations pour aboutir à ce que nous appelons aujourd’hui les trois lois de Kepler, qui sont enseignées en classe de Terminale S, et fondent l’astronomie moderne qui a émergé au XVIIe siècle.
Stéphane Le Gars
© APMEP Septembre 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
En 2017, Guy Boistel et Stéphane Le Gars présentent le Kepler Music Project 2.0, une nouvelle version du spectacle qui applique la méthode de Kepler aux exoplanètes découvertes par milliers depuis 1995. Par ce biais, le Kepler Music Project (KMP) ambitionne de faire découvrir la démarche extravagante de Kepler dans sa quête de la Vérité, mais également d’appliquer cette démarche sur des objets célestes récemment découverts, et ainsi susciter des questionnements chez le spectateur : qui est ce Kepler qui, en cherchant l’Harmonie du Monde découvre la façon dont les planètes tournent autour du Soleil ? Dans quel contexte a-t-il évolué ? En quoi son adhésion à l’héliocentrisme, sur les traces de Copernic, lui a-t-elle pavé le chemin vers la découverte ? En quoi la démarche de Kepler est-elle universelle ? Quelle est la part d’arbitraire dans sa construction théorique du Monde ? Quels choix opère-t-il pour articuler musique, arithmétique (les sciences du discontinu dans le quadrivium) avec géométrie et astronomie (les sciences du continu) ?

La démarche de Kepler mise en en scène dans le Kepler Music Project3
Kepler publie en 1596 son premier ouvrage, le Mysterium Cosmographicum. Il y montre déjà les fondements et particularités de sa pensée : il se montre influencé tout à la fois par Pythagore et l’idée que le monde est structuré par les nombres, et par la Bible car pour lui « Le Soleil au milieu des astres mouvants, lui-même immobile, mais source de mouvement, porte l’image de Dieu le Père, le Créateur… Il répand sa force motrice dans un médium qui contient les corps en mouvement de même que le Père crée par l’intermédiaire du Saint-Esprit »4. Le copernicanisme de Kepler, évident par son adhésion à l’héliocentrisme qu’il enseigne à l’université de Tübingen, déplaît fortement aux autorités religieuses, ce qui le conduit à une promotion sous forme d’exil : il est nommé professeur de mathématiques à Graz, éloigné de 600 km de Tübingen. C’est donc à Graz, devant ses étudiants, que Kepler dessine, d’un point de vue héliocentrique, les rapprochements de Jupiter et Saturne. Il réalise que ces deux planètes se rencontrent tous les 20 ans et divisent le cercle en 3, et que leurs orbites représentent des cercles inscrits dans des triangles équilatéraux : Kepler va alors chercher à trouver l’harmonie au cœur du système planétaire, harmonie qu’il trouvera non dans les polygones mais dans les polyèdres réguliers dits platoniciens, qui sont au nombre limité de 5 : ces polyèdres viennent remplir les espaces entre les orbites des six planètes ; ils sont parfaitement symétriques ; tous les sommets des polyèdres touchent les sphères dans lesquelles on peut les inscrire. Kepler trouve alors la raison du nombre limité des 6 planètes connues à son époque !
Animation 1 ![]() : les solides platoniciens organisent le Monde (nous remercions le Planétarium de Milan pour nous avoir permis d’utiliser cette animation).
: les solides platoniciens organisent le Monde (nous remercions le Planétarium de Milan pour nous avoir permis d’utiliser cette animation).
En 1600, Kepler quitte Graz pour Prague, où il va travailler avec Tycho Brahé qui réalise les observations les plus précises du moment. Il y découvre que l’orbite de Mars n’est pas circulaire mais elliptique, et précise même que cette planète balaie des aires égales en des temps égaux. Il publie ses réflexions en 1609 dans son Astronomia Nova, qui contient ce que nous appelons aujourd’hui les deux premières lois de Kepler.
Mais c’est en 1619 que paraît son Harmonices Mundi, ou Harmonie du Monde, ouvrage dense qui mêle mathématiques, astronomie et musique. C’est en effet en réutilisant la musique des sphères, sur les traces de Pythagore, que Kepler va pouvoir généraliser ses résultats obtenus sur Mars. Ce concept de musique des sphères se base sur l’idée que la musique est le lien entre l’homme et le cosmos. Pour les pythagoriciens, il existe une harmonie universelle dont les nombres sont l’expression sensible : l’harmonie, qu’elle soit cosmique ou musicale, est un état d’équilibre entre divers éléments, régi par des rapports numériques5. C’est donc par le concept d’harmonie, fondé sur une grande analogie cosmique, que Kepler espère découvrir le secret du monde : il s’agit pour lui de trouver les rapports harmoniques qui sont au cœur des sons comme au cœur du système solaire. Pour Kepler, « le musicien comme l’astronome imitent Dieu qui a créé le Monde en appliquant les lois géométriques ».
Depuis Pythagore et jusqu’à la Renaissance, seuls trois intervalles sont estimés consonants car, issus de rapports de nombres entiers, ils respectent la vénération des chiffres 1, 2, 3 et 4 (la tetraktys : 1+2+3+4=10) érigée en système philosophique par les pythagoriciens :
| Octave | Quinte | Quarte |
| 2/1 | 3/2 | 4/3 |
| 2,000 | 1,500 | 1,333 |
(aujourd’hui, nous disons par exemple qu’un son de fréquence 600 Hz est situé à un intervalle de quinte d’un son de fréquence 400 Hz car ces deux sons sont caractérisés par un rapport numérique \(600/400 = 3/2\) )
Au XVIe siècle, ces rapports sont revus par Zarlino dans le cadre de la gamme dite naturelle. Dans ce cadre, d’autres chiffres que 2 et 3 peuvent être utilisés pour définir les intervalles :
| Seconde | Tierce majeure | Tierce mineure | Sixte majeure | Septième |
| 9/8 | 5/4 | 6/5 | 5/3 | 15/8 |
| 1,125 | 1,250 | 1,200 | 1,667 | 1,875 |
Influencé tout à la fois par la théorie pythagoricienne de la musique, le concept de musique des sphères, l’héliocentrisme copernicien et par les nouvelles observations astronomiques, Kepler cherche les nombres qui sous-tendent l’harmonie universelle, et donc les mouvements des planètes.
Tout d’abord, il lui faut construire de nouveaux termes : « Pour éviter des erreurs, il m’a fallu faire reposer le fondement du Monde pour ainsi dire au centre du Soleil ; cela a entraîné que les lieux du Zodiaque, où les planètes sont les plus proches ou les plus éloignées, ne peuvent plus garder leur nom d’apogée ou de périgée, comme le fait abusivement Copernic, mais ont reçu de moi un nom propre et signifiant : aphélie et périhélie ».
Ensuite, Kepler attribue à chaque planète une note fondamentale caractéristique de sa vitesse lors du passage à l’aphélie (plus une planète est proche du Soleil, plus elle va vite et plus sa note se trouve dans les aigus).
Enfin, Kepler transforme la variation de vitesse entre l’aphélie et le périhélie en une variation de son, c’est à dire en un intervalle musical. Par exemple, les données les plus récentes dont Kepler dispose pour Saturne montrent que cette variation de vitesse correspond au rapport 5/4 ou 1,25, qui est l’intervalle de tierce majeure dans la musique pythagoricienne. Kepler va appliquer cette démarche pour l’ensemble des planètes connues à son époque (Mercure, Vénus, Terre, Mars, Jupiter, Saturne) et préciser son harmonie céleste, pour définir « quelle planète chante la voix de soprano, laquelle celle d’alto, celle de ténor et celle de basse » : il affirme alors que Mercure est le soprano, Vénus le contralto, Mars le ténor léger, tandis que Jupiter et Saturne chantent les basses profondes. Il attribue ainsi une gamme à chaque planète en utilisant donc deux paramètres : la distance de la planète au soleil (ce qui donne la note fondamentale de la gamme), et son excentricité (qui lui donne l’étendue de la gamme, comme on le voit bien pour Vénus dont l’excentricité est quasi-nulle).

Figure 1 : Notre système solaire mis en musique par Kepler
C’est donc en se fondant sur la musique des sphères, sur l’harmonie universelle, que Kepler trouve ce que nous appelons aujourd’hui la troisième loi de Kepler ou loi Harmonique qui donne le rapport entre les mouvements et les distances : le rapport \(T²/a^3\) est le même pour toutes les planètes6. Comme l’écrit Kepler dans l’Harmonie du Monde :
« La proportion des moyens mouvements diurnes est donc trouvée à partir des Harmonies fixées […]. En effet, la proportion des moyens mouvements est une fois et demie la proportion inverse des Orbes. ».7
L’application des lois de Kepler au exoplanètes : une démarche anachronique ?
L’idée d’appliquer la méthode de Kepler aux exoplanètes a émergé progressivement au sein du Kepler Music Project. Ceci pour plusieurs raisons : actualiser et moderniser le spectacle, de façon à lui assurer des perspectives pédagogiques en lycée ; générer des gammes comme Kepler l’a fait pour le système solaire ; permettre une réflexion épistémologique sur la méthode de Kepler.
Actualiser la démarche de Kepler
La première version du Kepler Music Project envisageait de donner à comprendre la démarche de Kepler, avec une scénarisation qui mettait en parallèle deux personnages : un historien des sciences contemporain (joué par Guy Boistel par ailleurs pianiste) et Kepler lui-même (joué par Stéphane Le Gars par ailleurs saxophoniste). La version 2.0 du spectacle, donnée à Nantes plusieurs fois à partir de l’automne 2017, et dans le cadre du festival Jazz au Vip à Saint-Nazaire, conclut la partie conférence du spectacle (avant un concert electro-jazz inspiré des gammes de Kepler) par une rencontre anachronique entre ces deux personnages autour des exoplanètes, autorisant un dialogue entre le savant du XVIIe siècle et un historien des sciences d’aujourd’hui. Cet artifice temporel permet de poursuivre le travail mathématique, entrepris par Kepler, sur un système planétaire découvert par le satellite Kepler, mis en orbite par la NASA en 2009 pour découvrir des exoplanètes semblables à la Terre autour d’étoiles proches : ![]() .
.
Le premier critère sur lequel se baser pour le choix d’un système planétaire est en premier lieu le nombre de planètes. Cette recherche peut se faire sur des sites internet comme exoplanets.org ou exoplanet.eu via des tables interactives permettant de sélectionner les exoplanètes selon des critères comme période, excentricité ou demi-grand-axe. Nous avons choisi pour le spectacle d’étudier le système Kepler-62 : celui possède 5 planètes, avec des excentricités différentes (donc des intervalles musicaux variés), et l’une des planètes située dans la zone d’habitabilité. Un travail plus approfondi (y compris avec des élèves) est possible grâce au logiciel Nasa’s Eyes disponible sur le site de la NASA : ![]() .
.
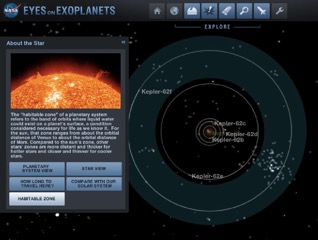
Figure 2 : le système Kepler-62 d’après le logiciel Nasa’s Eyes
Générer des gammes musicales à partir des exoplanètes
Pour appliquer la méthode de Kepler à n’importe système planétaire, nous avons construit des outils informatiques : fichier Excel tout d’abord, puis page web interactive.
Le fichier excel (voir fichier joint « Kepler62 ») a été une première étape pour faire « chanter » ce système, mais nous avons par la suite envisagé de construire un outil permettant à tout un chacun, sur n’importe quel système planétaire, d’obtenir l’intervalle de la planète comme évoqué dans le spectacle pour le système solaire. La page web est en cours de construction, mais il est d’essence du Kepler Music Project d’être un projet en chantier permanent et de montrer des résultats encore provisoires (qui peuvent être améliorés par les suggestions de tous) : © ![]() .
.
Cette page web, provisoire, renvoie au site Thimble qui permet l’écriture de pages web en ligne, et autorise la lecture du code via le bouton « Remixer ».
Nous avons alors créé le système musical suivant :

Figure 3 : le système musical Kepler-62
Une version sonore est également disponible :
Critiquer la démarche de Kepler
En mettant « la main à la pâte », c’est-à-dire en construisant le canon planétaire d’autres systèmes, sur la base des travaux de Kepler, nous pouvons en savoir plus sur les choix et les libertés prises par le savant du XVIIe siècle.
Une telle critique nécessite tout d’abord de replacer Kepler dans son contexte. Au XVIIe siècle, les sciences enseignées dans les Universités sont structurées au sein du Quadrivium qui regroupe l’arithmétique, la géométrie, l’astronomie et la musique (cette dernière fait partie intégrante des sciences). Musique et arithmétique sont les sciences des quantités discrètes respectivement en mouvement et au repos, alors que géométrie et astronomie représentent les sciences des quantités continues au repos et en mouvement. D’après Brigitte Van Wymeersch8, Kepler, dans sa méthode, bouleverse cet ordre hérité de Pythagore, en considérant la musique comme une quantité continue, non discrète. Cette approche explique la façon avec laquelle Kepler attribue des sons aux planètes sur leurs orbites elliptiques : il associe une note grave lors du passage de la planète à l’aphélie, et une note aigue lors de son passage au perihélie. Mais l’ensemble de l’ellipse produit du son, dont certains points seulement occupent une place privilégiée dans la recherche de l’Harmonie. La recherche de ces points passe également par une attention à l’ensemble des planètes, qui doivent produire des accords consonants lorsqu’elles se trouvent au même moment à certains points de leurs orbites, conduisant au canon planétaire.
Dans notre réplication de la démarche de Kepler, écrire la gamme d’une planète est donc un exercice difficile : sur quel critère trouver les notes musicales (donc des quantités discrètes) dans le continuum sonore qu’est un intervalle entre deux sons donné par l’excentricité de la planète ? Quelle part de subjectivité intervient alors ? Comment le contexte culturel, et en particulier musical, joue-t-il dans cette recherche du discontinu sonore, si l’on réalise que la consonance en musique est un phénomène historiquement daté (par exemple : la tierce majeure a longtemps été considérée comme une dissonance ou une consonance imparfaite avant d’être progressivement acceptée comme consonance notamment suite aux travaux de Rameau) ?
Par ailleurs, la notion de point de repère prend ici tout son sens : quelle note fondamentale attribuer pour chaque gamme planétaire ? Si l’on considère, comme Kepler, que c’est la planète la plus éloignée qui fixe la basse, quelle note lui attribuer ? Là encore, c’est la pratique musicale qui donne la solution à Kepler, notamment via les possibilités des chanteurs de son époque.
Conclusion
Le Kepler Music Project est un spectacle évolutif (il se joue à deux musiciens, mais une version quartet – avec un batteur et un bassiste- existe également), qui vise à donner à voir une méthode, une histoire, et surtout donner à entendre des musiques qui ont une histoire et sont situées entre recherche scientifique objective et expression subjective. L’esthétique qui s’en dégage est donc un compromis entre objectivité et subjectivité, entre raisonner et résonner. C’est une expérience à tenter qui parle à la fois à l’esprit et au corps !
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Stéphane Le Gars est membre du Centre François Viète, Nantes.
-
De nombreuses informations sont disponibles sur notre site :
 ainsi que sur la page Facebook :
ainsi que sur la page Facebook :  ↩
↩ -
Par exemple :
 ↩
↩ -
Ce paragraphe reprend en partie l’article que j’avais écrit en 2015 : LE GARS Stéphane, « Kepler, les astres et la musique », Les Cahiers Clairaut, Automne 2015, p.23.↩
-
Toutes les citations de Kepler sont extraites des traductions françaises du Mysterium cosmographicum (Le secret du Monde, trad. A. Segonds, 1984, Les Belles-Lettres), de l’Astronomia Nova et de L’Harmonie du Monde par Jean Peyroux, Paris, A. Blanchard.↩
-
Van Wymeersch Brigitte, Descartes et l’évolution de l’esthétique musicale, Mardaga, 1999, p.27.↩
-
T est la période de la planète, a est la longueur du demi-grand axe de l’ellipse.↩
-
Kepler Jean, L’Harmonie du Monde, traduit pour la première fois du latin en français avec un un avertissement et des notes par Jean Peyroux, Librairie Blanchard, Paris, 1979, p.373.↩
-
Van Wymeersch Brigitte, Descartes et l’évolution de l’esthétique musicale, Mardaga, 1999, p.52.↩
