Mathématiques à/en portée

Le langage mathématique et le langage musical ont ceci de particulier que les mots, les signes, les symboles n’y désignent pas seulement des objets : ils les incarnent [6]. Mieux : mathématiques et musique se parlent et se comprennent, au point que leur dialogue fut souvent fructueux : l’étude méthodique du monocorde, attribuée à Pythagore; la pratique, en amateur, de la guitare par Zorn ; l’usage des probabilités par Xenakis ; l’emploi des transformations géométriques par Bach en sont autant d’exemples. Et si les deux disciplines ont leur grammaire, axiomes et théorèmes dans un cas, solfège et harmonie dans l’autre, elles demandent à l’esprit de se libérer de la technique (donc de la posséder) pour être créatif, et ne se renouvellent que parce qu’elles savent perpétuellement réinventer et dépasser leurs règles [10][3]. En voici un aperçu, à la portée du collégien.

Karim Zayana

© APMEP Juin 2018

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

La portée mathématique du langage musical

Figure 1 : Portée.↩

Quand on lit de la musique, on fait déjà, sans le savoir des mathématiques. Une portée, c’est un axe horizontal — axe des temps, et un axe vertical — axe des notes, lesquelles notes sont indissociablement liées à des fréquences, et donc des nombres. Ajoutons une origine, marquée par la clé qui sert de référence, figure 1. Petit raffinement : l’axe vertical n’est, en vérité, pas gradué linéairement mais logarithmiquement. Quand on franchit un barreau, du DO au RÉ par exemple, on multiplie en fait la fréquence par à peu près 9 / 8. Et quand on passe d’un MI au FA, on la multiplie à peu près par la racine carrée de ce nombre, \(\sqrt{9/8}=3/2\sqrt{2}\). Autre fait remarquable : nous venons de décrire ce qui s’apparente à la représentation graphique d’une fonction telle que nous la rencontrons communément aujourd’hui. En cela, la musique avait quelques siècles d’avance sur les mathématiques, qui n’ont adopté ce mode d’explicitation qu’au XVIIe siècle.

Figure 2 : Portée avec symétrie.↩

Une portée musicale, nous l’avons dit, c’est un repère. Et la géométrie s’invite dès lors spontanément. On va reconnaître, sur certaines partitions, les effets de transformations du plan : translations et symétries ou association des deux. La translation horizontale traduit un décalage temporel, qu’on retrouve dans l’écriture du canon. La translation verticale est, elle, plus ou moins une transposition, c’est-à-dire que l’on joue un même motif plus aigu ou plus grave. La symétrie axiale verticale retourne un motif ou une phrase entière sur elle-même, le tour de force consistant à ce que les deux s’accordent et puissent être joués ensemble. La symétrie axiale horizontale dédouble une voix en une autre, dans un mouvement descendant pour cette seconde s’il était ascendant pour la première. Au moins deux compositeurs majeurs ont utilisé ces procédés, et les ont même combinés. Citons, chronologiquement, Bach (allemand, XVIIIe) puis Mozart (autrichien, XVIIIe) figure 2.

Les probabilités et les statistiques trouvent en musique un champ d’application. Dans une tonalité donnée, certaines notes reviennent plus souvent que d’autres : on parle de degrés forts et de degrés faibles. On peut se livrer, sur une partition donnée, à un décompte comparatif des occurrences de chacune des notes. On peut aussi y inclure des pondérations en fonction des valeurs des notes, c’est-à-dire de leur durée. En probabilités, mentionnons que des compositeurs ont investi le terrain de la musique stochastique, tirant au sort les notes, leur durée, l’instrument qui les exécute selon un hasard rigoureusement contrôlé. Le compositeur grec Xenakis (XXe) était passé maître dans cet art.

La corde sensible

Le calcul sur les puissances, les fractions, la proportionnalité, les racines, voire même le calcul modulaire, jouent un rôle central en solfège, bien que l’on puisse faire de la musique en ignorant les détails conceptuels qui la sous-tendent. Les puissances de deux interviennent par exemple dans la division du temps. Il est un sujet plus riche, à savoir la construction de la gamme, ou, devrions-nous dire, des échelles musicales, tant il y en eut, à travers les âges.

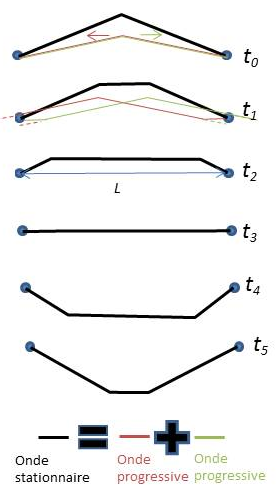
Figure 3 : Ondes.↩

Commençons par de la physique en prenant une corde, de longueur L, tendue en ses deux extrémités. C’est déjà un instrument de musique, même rudimentaire. Pinçons-la. Cela l’écarte de sa position d’équilibre. L’élongation va se propager dans les deux sens, atteindre les bouts (tête et chevalet dans le cas d’une guitare), s’y réfléchir, parcourir le même chemin en sens inverse, rebondir de nouveau, etc., figure 3 (en trait épais l’allure de la corde, comme superposition de deux ondes progressives, en traits fins). À l’affaiblissement près, le phénomène est périodique et produit un son. Pour entendre mieux qu’un fouettement dans l’air, la corde doit être fixée sur une table qui sert de caisse de résonance. Il s’en échappe ce qu’on appelle dans le langage courant une note.

À l’œil nu, on ne voit rien tant la vibration est rapide : songez que la cadence est de l’ordre de 440 aller-retours par seconde pour une note LA, plus exactement un LA3 à savoir le LA donné par un diapason. Pour mieux percevoir les choses, il faut faire l’expérience avec une grosse corde : bout marin ou d’escalade. Et là, on peut suivre du regard la propagation aller-retour de l’onde de choc qui, certes, s’évanouit assez vite. Que constate-t-on aussi ? Et bien que plus la corde est tendue, plus la propagation de la secousse est rapide ; mais ceci ne se fera pas tout à fait dans un rapport de proportionnalité (le rapport est quadratique en vérité). Bien sûr, plus la corde est courte, plus la période est courte car la distance à parcourir à l’onde est plus courte. Là, si fait, il y a rapport de proportionnalité. Enfin, signalons l’influence de la matière dont est faite la corde. C’est pour cela qu’on voit les choses sur une corde de marin, et pas sur une corde de guitare.

À la guitare, justement, on joue sur la tension des cordes à l’aide des mécaniques. Les cordes ont toutes la même longueur, mais on peut les raccourcir, sans changer la tension, en appuyant dessus. La partie qui va de la tête au doigt devient inerte, la partie restante entre en vibration. Enfin, les cordes sont de matériaux et de diamètres différents : cela explique qu’à tension égale, certaines sonnent plus aigu ou plus grave.

Aux temps reculés du grec Pythagore (500 avant J.-C.), on avait déjà conscience que la taille d’un objet qui entrait en résonance influait sur la note produite. Notamment, on avait perçu que deux objets comparables (en l’occurrence, des enclumes frappées par un marteau) mais aux masses de 2 pour 1 sonnaient pareil, quoique l’un plus aigu que l’autre. On donnera le même nom aux notes ainsi émises et on appellera l’octave l’intervalle de fréquence qui les sépare. On avait aussi réalisé que deux objets comparables mais aux masses de 3 pour 2 sonnaient bien — on dira harmonieusement — ensemble. Cela peut s’expliquer par la théorie du français Fourier (XIXe siècle).

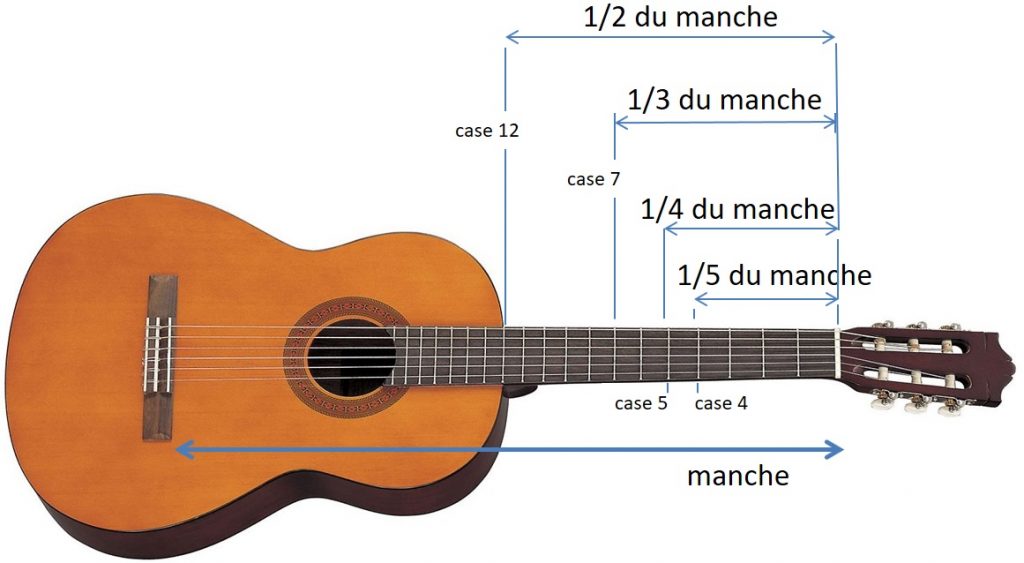
Figure 4 : Guitare.↩

Sur une guitare, appelons MI la note de la corde à vide la plus aiguë (la chanterelle) d’où l’on part, et cela même si les noms des notes furent bien postérieurs à Pythagore. Appuyons en case 12, on raccourcit le manche de moitié. La première moitié est inerte, l’autre moitié vibre. La fréquence émise est double de la corde à vide, nous avons produit l’octave, encore un MI, figure 4. Puis appuyons en frette 7, on raccourcit le manche d’un tiers. Les deux tiers restants produisent une fréquence fois plus élevée que la corde à vide. La note 3 / 2 fois plus élevée fait faire un intervalle dit de quinte. C’est celle que nous baptiserons SI. Nous pouvons continuer ainsi, bâtir la quinte de la quinte, etc.

Pour simplifier, commençons plutôt à DO, qui sera notre tonique. Sa quinte fournit le SOL. La quinte de la quinte, à la fréquence 9 / 4 de la fondamentale, mais aussi après retour dans l’octave, est un RE. Continuons avec la fréquence 27 / 8 de la fondamentale, ou encore 27 / 16 après retour dans l’intervalle d’octave, c’est le LA. Ainsi de suite jusqu’à obtenir 7 notes que nous désignons1 par DO, SOL, RÉ, LA, MI, SI, FA#. Autant de notes que de jours, ou que d’astres mobiles connus à l’époque. Continuons en si bon chemin: DO#, SOL#, RÉ#, LA#, MI#… SI# est la douzième quinte, correspondant à (3 / 2)12, ou encore, après retour à l’octave, à 312 / 219, soit 1,01 fois la fréquence fondamentale. C’est un petit miracle : la spirale de quintes est pratiquement un cycle, figure 5.

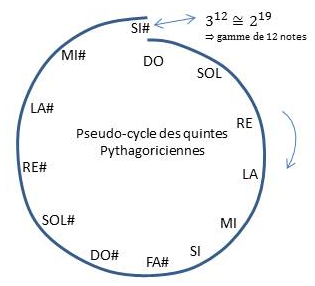
Figure 5 : Gamme de 12 notes.↩

On assimile donc ce SI# au DO, tout en sachant qu’on commet une petite erreur2. La dernière quinte est fausse, c’est la quinte du loup. Quand on joue le DO et le SI#, la superposition des deux notes crée un battement, comme une sirène, qui fait penser au hurlement d’un loup et qui résulte de la formule d’addition de deux sinusoïdes.

L’accord parfait

Gamme chromatique
import win sound
from numpy import *
q = 3/2 # saut d’une quinte
notes = [262] # fréquence du DO3
octave = notes[0]*2
for i in range(11):
frequence = notes[i]*q
while fréquence > octave:
frequence = frequence/2
notes.append(fréquence)
notes.sort() # ordonné selon fréquences croissantes
for note in notes:
winsound.Beep(int(floor(note)), 300)
print(int(floor(note)))

Fort des douze notes que nous avons obtenues par superposition de quintes selon le procédé de Pythagore, nous aboutissons à la gamme dite chromatique. Ce script Python permet de retrouver tout cela à la volée, de réordonner les notes et de les écouter.

L’oreille est sensible au rapport des fréquences, et non à leur différence. On mesure donc les intervalles de fréquences par une division et non une soustraction. De DO à DO#, l’intervalle est de 1,067 environ (37 / 212 précisément) ; de DO# à RÉ il est de 1,053 (28 / 35 précisément) ; de RÉ à RÉ# de 1,067 ; de RÉ# à MI de 1,053 ; de MI à FA de 1,067 ; de FA à FA# de 1,053 ; de FA# à SOL de 1,053 ; de SOL à SOL# de 1,067 ; de SOL# à LA de 1,053 ; de LA à LA# de 1,067; de LA# à SI de 1,053 ; de SI à DO de 1,053.

Les demi-tons ne sont pas réguliers, les tons non plus: certains ont une amplitude de \(1,053^2\simeq1,108\), d’autres de \(1,053\times1,067\simeq1,123\). On va tout de suite « voir » que c’est un inconvénient.

Soit la comptine universellement connue Au clair de la Lune mon ami Pierrot : DO DO DO RÉ MI RÉ DO MI RÉ RÉ DO. À supposer qu’on souhaite la jouer ou la chanter un peu plus haut, mettons deux tons et demi au-dessus, parce qu’on n’a pas le bon instrument, qu’on a mis un capodastre ou que c’est une tessiture qui nous convient mieux. On fait donc ce qu’on appelle une transposition. La mélodie devient avec l’échelle de Pythagore dont on dispose : FA FA FA SOL LA SOL FA LA SOL SOL FA. Et… ça ne sonne pas pareil car les intervalles de fréquence (au sens des rapports) ne sont pas tout à fait identiques : l’écart FA-SOL n’est pas l’écart DO-RÉ. Ceci a commencé à devenir critique au siècle quand les compositeurs ont éprouvé le besoin d’adapter leurs œuvres à tous les instruments, et de faire jouer les musiciens ensemble.

La gamme de Pythagore comporte des quintes, et, par renversement, des quartes. Expliquons. De DO à SOL plus aigu, le rapport est de 3 / 2. De SOL à DO plus grave, le rapport est de 2 / 3. Enfin, de SOL à DO plus aigu le rapport est de 2 × 2 / 3. Voilà qui définit l’intervalle de quarte. On peut obtenir la quarte sur la guitare en case 5 : nous sommes au quart du manche, il reste les 3 / 4 qui vibreront à la fréquence 4 / 3 de la fondamentale, figure 4. Il existe d’autres consonances agréables, que la théorie de Fourier expliqua postérieurement. Appuyons en case 4. Il reste les 4 / 5 du manche, soit une fréquence 5 / 4 de la note à vide. Voilà qui définit l’intervalle de tierce. Que nous n’avons pas rigoureusement dans la gamme de Pythagore, mais que nous avons3 sur la guitare. Au XVIe siècle, le compositeur italien Zarlino va l’introduire dans une nouvelle échelle. Pour autant, cette dernière ne sera pas plus performante en matière de transposition.

Nous en arrivons donc à une troisième échelle, qui s’est imposée en Occident et ce depuis le siècle. Il s’agit du tempérament égal, dont le Clavier bien tempéré de Bach, même s’il ne s’y plie pas encore tout à fait, donne un avant-goût. On reste sur un principe de 12 notes. On égalise tous les demi-tons. C’est-à-dire qu’on escalade d’une note au demi-ton supérieur en dilatant la fréquence par d’une même constante multiplicative q. Après 12 telles opérations, on a décrit l’octave, d’où q12 = 2 et \(q=\sqrt[12]{2}\) est la racine, non pas carrée, mais douzième de 2, soit environ \(1,059\) (à comparer aux \(1,053\) et \(1,067\) de tout à l’heure). La transposition est dès lors exacte. En revanche, du fait du tempérament égal, les tierces, et les quartes ou les quintes ainsi que les accords mineur ou majeur ne sont pas tout à fait purs. Et les cases de la guitare ne sont pas exactement réparties dans les rapports rationnels de la figure [4]. De quoi faire chanter « faux » Léonard Cohen et Jeff Buckley :

Well I heard there was a secret chord
That David played and it pleased the Lord
But you don’t really care for music, do you?
Well it goes like this: the fourth, the fifth
The minor fall and the major lift
The baffled king composing Hallelujah

En guise d’approfondissement, on consultera les références [1], [2], [3], [5], [7], [8] et la fin de [4] et [9].

Karim Zayana est Inspecteur Général, professeur invité à l’Institut Mines-Télécom. L’article est extrait d’un atelier[4] proposé aux journées nationales de l’APMEP (Nantes, 2017) et d’une conférence[9] donnée à la cité internationale Balzac (Paris, 2015).

Références

  1. Collectif. « Maths et musique ». In : Tangente hors-série no 11 (2010). ↩ ↩
  2. Rémi Coulon. Maths et Musique.  ↩
  3. Zoé Faget. Musique et mathématiques : recherche et création. ↩
  4. Frédéric Hérau et Karim Zayana. Atelier réalisé aux journées nationales de l’APMEP (Nantes, 2017).  2017. ↩
  5. Xavier Hubaut. Pourquoi n’ai-je jamais rien compris au solfège ? ↩
  6. Laurent Lafforgue. L’enseignement des mathématiques. Séminaire « Quel enseignement secondaire4 pour le XXIe siècle ? »  2016.↩
  7. David Louapre et Vled Tapas. Les mathématiques de la musique.  ↩
  8. Nicolas Minet. « 7 notes dans la gamme. Toujours ? Pourquoi ? » In : PLOT no 21 (2008).  ↩
  9. Nicolas Ngo et Karim Zayana. Conférence jouée en 2015 à la cité internationale Balzac (Paris). v. 2015. ↩
  10. Charles Torossian et Cédric Villani. 21 mesures pour l’enseignement des mathématiques.  Fév. 2018.↩
  1. Les Grecs ne les désignaient pas par ces noms. Ce sont des moines du XIe siècle qui les ont ainsi baptisées. ↩
  2. Cette erreur (appelée comma) est à la musique ce que l’epsilon est aux mathématiques.↩
  3. La guitare n’est pas un instrument pythagoricien. Ce n’est pas non plus tout à fait un instrument « Fourierien ». C’est un instrument tempéré, cf. paragraphe suivant.↩
  4. C’est pourtant un sujet majeur.↩
Pour citer cet article : Zayana K., « Mathématiques à/en portée », in APMEP Au fil des maths. N° 528. 9 juin 2018, https://afdm.apmep.fr/rubriques/ouvertures/mathematiques-a-en-portee/.