Triangulation et impression 3D
Imprimer en 3D est une belle occasion de faire des mathématiques. Dans cet article complété par un second disponible uniquement en ligne, Aurélien Alvarez nous initie à l’impression 3D à travers quelques éléments de mathématiques, de technologie et d’informatique.
Aurélien Alvarez
© APMEP Juin 2019
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Avec du papier, une règle, un peu de colle et une paire de ciseaux, c’est une activité bien plaisante que de construire les cinq polyèdres réguliers. C’est une activité bien différente, mais tout aussi plaisante, que de les imprimer. Nous expliquons dans cet article le lien entre polyèdres, triangulation des surfaces et impression 3D. Dans un second article [1], disponible en ligne, nous nous attardons plus spécifiquement sur le cas du tétraèdre et expliquons en détail comment préparer un fichier pour l’impression.

Si vous n’avez jamais imprimé d’objets mais que l’idée de vous y mettre vous plaît bien, alors ces deux articles pourront peut-être vous aider à faire vos premiers pas.
Impression 3D et format STL
Le principe général de l’impression 3D
Le principe général du fonctionnement d’une imprimante 3D est de fabriquer des volumes solides par ajout progressif de matière. Avant de pouvoir lancer l’impression d’un objet, il faut d’abord disposer d’un modèle numérique 3D de celui-ci. Le fichier du modèle 3D est ensuite analysé par le logiciel d’impression de l’imprimante qui est en charge d’organiser le découpage en tranches des différentes couches de matière qui seront déposées les unes sur les autres afin de fabriquer l’objet. Le logiciel d’impression de l’imprimante convertit donc le modèle 3D en instructions précises que la machine est capable de comprendre et d’exécuter. L’imprimante dépose finalement la matière couche après couche, lentement mais sûrement, jusqu’à obtenir le volume souhaité.
 |
 |
 |
 |
 |
 |
À leurs débuts, les imprimantes 3D utilisaient bien souvent des résines, alors que depuis les années 2010, d’autres matériaux sont plébiscités, en particulier certains plastiques comme le PLA ou l’ABS. C’est d’ailleurs le cas de l’imprimante da Vinci 1.0 Pro 3in1 ![]() que nous avons utilisée ici.
que nous avons utilisée ici.
-
Le PLA est biodégradable et issu de matériaux recyclés. Il est assez courant de l’utiliser dans l’industrie alimentaire (comme emballage !). Il ramollit autour de \(50 °C\), commence à fondre à \(160 °C\) et peut être réellement travaillé à partir de \(180 °C\). En plus d’être sensible à l’humidité, le PLA a tendance à casser facilement si on le contraint trop fortement.
-
L’ABS quant à lui est un polymère thermoplastique que l’on retrouve dans les appareils électroménagers ou dans les jouets Lego. Il ramollit autour de \(90 °C\), commence à fondre à \(180 °C\) et peut être réellement travaillé vers \(230 °C\). Il est donc plus résistant à la chaleur que le PLA et se plie facilement sans rompre.
Le PLA et l’ABS ont chacun leurs avantages et leurs inconvénients mais il est en général plus facile de réaliser des impressions avec le PLA qu’avec l’ABS car ce dernier résiste mal aux chocs de température. Bien choisir entre le PLA ou l’ABS selon l’objet que l’on souhaite imprimer est davantage une question d’expérience que de science…
Le format STL
De nombreux logiciels de modélisation sont disponibles, y compris des logiciels gratuits et multiplateformes. Ces logiciels permettent de modéliser des formes géométriques complexes à l’aide d’outils de base très simple, comme par exemple l’outil d’extrusion. Une fois le logiciel pris en main et avec un peu d’habitude, on peut modéliser un tétraèdre et un cube en quelques clics, comme illustré sur l’image suivante extraite du logiciel SketchUp ![]() .
.
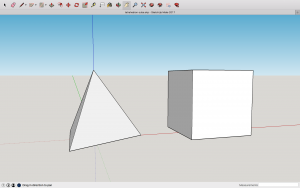
Pour imprimer le tétraèdre ci-dessus, il nous suffit alors de demander à notre logiciel de modélisation d’exporter le modèle 3D vers un fichier au format STL qui sera traité par le logiciel d’impression de l’imprimante. Le temps d’impression dépend essentiellement de la taille de l’objet à imprimer et du taux de remplissage de celui-ci : cela peut donc aller de quelques minutes à de longues heures. Pendant ce temps, avec un simple éditeur texte, rien n’interdit de jeter un œil au fichier STL en question.
On découvre alors quelque chose comme ceci :
solid tetrahedron
facet normal 0.0 0.942809 0.333333
outer loop
vertex 70.7107 72.4745 -70.7107
vertex -70.7107 72.4745 -70.7107
vertex 0.0 31.6497 44.7594
endloop
endfacet
facet normal 0.816497 -0.471404 0.333333
outer loop
vertex 70.7107 72.4745 -70.7107
vertex 0.0 31.6497 44.7594
vertex 0.0 -50.0 -70.7107
endloop
endfacet
facet normal -0.0 0.0 -1.0
outer loop
vertex 70.7107 72.4745 -70.7107
vertex 0.0 -50.0 -70.7107
vertex -70.7107 72.4745 -70.7107
endloop
endfacet
facet normal -0.816497 -0.471404 0.333333
outer loop
vertex -70.7107 72.4745 -70.7107
vertex 0.0 -50.0 -70.7107
vertex 0.0 31.6497 44.7594
endloop
endfacet
endsolid tetrahedron
Le format STL est très répandu de nos jours, son nom provient du mot stéréolithographie (STL pour STereo-Lithography). D’après Wikipédia :
La stéréolithographie est une technique, dite de prototypage rapide, qui permet de fabriquer des objets solides à partir d’un modèle numérique. L’objet est obtenu par superposition de tranches fines de matière. Le développement industriel de cette technique date des années 1980 et fut initiée aux États-Unis par Charles W. Hull.
Notons que le format de fichier STL ne décrit que la géométrie de surface d’un solide alors qu’un modèle numérique de conception assistée par ordinateur contient bien souvent des informations complémentaires comme la couleur, la texture, etc.
Regardons de plus près ce fichier. La première ligne contient le mot réservé solid suivi du nom que l’on a choisi pour l’objet au moment de l’exportation (ici tetrahedron) et la dernière ligne contient ce même nom après le mot réservé endsolid. Le reste du fichier est composé de blocs commençant par le mot réservé facet et terminant par le mot réservé endfacet.
facet normal ni nj nk
outer loop
vertex v1x v1y v1z
vertex v2x v2y v2z
vertex v3x v3y v3z
endloop
endfacet
À l’intérieur d’un bloc, les coordonnées de trois sommets sont indiquées, ainsi que les coordonnées de la normale au triangle formé par ces trois sommets et pointant vers l’extérieur du volume. Les coordonnées de la normale sont précédées par le mot réservé normal et celles de chacun des sommets par le mot réservé vertex. Dans notre exemple, on lit quatre blocs facet–endfacet correspondant chacun à l’une des quatre faces du tétraèdre. On vérifie également que les quatre normales indiquées dans le fichier sont bien des vecteurs de norme \(1\).
En résumé, un fichier STL contient essentiellement les données de triangulation de la surface de l’objet que l’on souhaite imprimer. Ainsi, tous les objets que l’on imprime, même s’ils peuvent sembler lisses quand on les prend en main, sont en fait décrits par une multitude (parfois des dizaines de milliers) de petits triangles plats. Si les triangles sont l’ADN du format STL, il n’est pas évident a priori que l’on puisse décrire toute surface comme une collection de triangles. Nous allons voir dans la suite de cet article un théorème fondamental de la topologie des surfaces compactes qui affirme que c’est en fait bien le cas.
Triangulation des surfaces
Le tétraèdre régulier est formé de quatre faces triangulaires et si l’on coupe par la diagonale chaque face carrée du cube en deux, on peut également voir le cube comme composé de \(2 \times 6\) triangles isocèles. L’octaèdre et l’icosaèdre ont respectivement huit et vingt faces triangulaires. Quant au dodécaèdre, ses douze faces sont des pentagones réguliers et il est très facile de diviser un polygone régulier à \(p\) côtés en \(p\) triangles isocèles en rajoutant un sommet au centre de celui-ci.
Quitte à parler de polyèdres réguliers et quitte à ouvrir une parenthèse dans notre propos, nous ne résistons pas au plaisir de donner ci-dessous deux démonstrations qu’il n’en existe que cinq, avant de nous intéresser au problème général de la triangulation des surfaces compactes.
Cinq polyèdres réguliers, pas davantage
Les polyèdres réguliers ou solides de Platon sont par définition les polyèdres convexes et réguliers de l’espace ordinaire. Chose étonnante au premier abord, il n’y en a qu’un nombre fini, cinq précisément, alors que les polygones réguliers du plan sont, eux, en nombre infini : quel que soit un entier naturel \(p\) au moins égal à trois, il existe un polygone régulier ayant \(p\) côtés et la démonstration revient essentiellement à découper le cercle unité du plan euclidien en \(p\) parts égales.
L’image suivante est extraite du film Dimensions[3] .
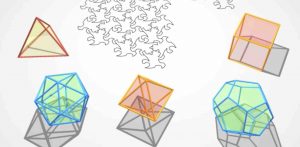
Les noms des polyèdres réguliers nous rappellent leurs nombres de faces : tétraèdre (pyramide à base triangulaire), hexaèdre (cube), octaèdre, dodécaèdre et icosaèdre. Au moins depuis les mathématiques grecques, les polyèdres réguliers fascinent par leur esthétique et leurs symétries. Par ailleurs, ils jouent un rôle important dans la philosophie de Platon qui, dans le Timée, l’un de ses derniers dialogues, associe chacun des quatre éléments avec un polyèdre régulier : le feu avec le tétraèdre, la Terre avec le cube, l’air avec l’octaèdre et l’eau avec l’icosaèdre. Et le dodécaèdre ? Platon (428-348 av. J.-C.) voit dans ce dernier le Tout, la quintessence. Quant à Euclide (\(\sim 300\) av. J.-C.), il a donné dans les Éléments une description mathématique complète des solides de Platon, de leurs propriétés à leur construction.
Afin de décrire la combinatoire d’un polyèdre régulier, on utilise le symbole \(\{p, q\}\) de Shläfli (1814-1895) :
-
\(p\) est le nombre de côtés de chaque face (c’est aussi le nombre de sommets de chaque face) ;
-
\(q\) est le nombre de faces se rencontrant en chaque sommet (c’est aussi le nombre d’arêtes partant de chaque sommet).
Les faces du tétraèdre sont des triangles équilatéraux, donc \(p\) est égal à trois. Par ailleurs, deux sommets distincts du tétraèdre sont toujours reliés par une arête, donc \(q\) est égal à trois également. Le symbole de Shläfli du tétraèdre est donc \(\{3, 3\}\). C’est un exercice facile que de calculer les symboles de Shläfli des autres polyèdres réguliers et on trouve \(\{4,3\}\) pour le cube, \(\{3, 4\}\) pour l’octaèdre, \(\{5, 3\}\) pour le dodécaèdre et \(\{3, 5\}\) pour l’icosaèdre.
Étant donné un polyèdre régulier, notons \(S\), \(A\) et \(F\) ses nombres de sommets, d’arêtes et de faces. Nous pouvons écrire plusieurs égalités :
-
\(p \times F = 2 A\) car une arête appartient toujours à deux faces exactement ;
-
\(q \times S = 2 A\) car une arête relie toujours deux sommets exactement ;
-
\(S – A + F = 2\), c’est la fameuse relation caractéristique d’Euler.
En combinant les deux premières égalités avec la troisième, on en déduit \[\frac{1}{q}-\frac{1}{2}+\frac{1}{p}=\frac{1}{A}\quad\text{et donc}\quad\frac{1}{p}+\frac{1}{q}> \frac{1}{2}\cdotp\]
Or \(p\) et \(q\) sont par définition des entiers naturels au moins égaux à trois, ce qui ne laisse que peu de choix pour les couples \(\{p, q\}\), à savoir \(\{3, 3\}\), \(\{3, 4\}\), \(\{3, 5\}\), \(\{4, 3\}\), \(\{5, 3\}\). On démontre ainsi qu’il existe au plus cinq polyèdres réguliers, les fameux cinq solides de Platon. Reste alors à les construire mathématiquement pour s’assurer qu’ils existent bien !
Remarquons qu’il est tout à fait possible de se convaincre qu’il existe au plus cinq polyèdres réguliers par un petit raisonnement géométrique, plutôt qu’en écrivant des égalités comme nous l’avons fait. On commence par remarquer qu’au voisinage de chaque sommet du polygone régulier il y a au moins trois faces (autrement dit que trois arêtes au moins partent de chaque sommet). Puisque la somme des angles des faces au voisinage d’un sommet ne peut excéder \(360 °\) et que chaque face contribue à part égale, on en déduit que l’angle au sommet d’une face est strictement inférieur à \(\dfrac{360}{3}= 120 °\). Il ne reste plus qu’à faire la liste des polygones réguliers « admissibles », parmi lesquels :
-
le triangle équilatéral avec un angle de \(60 °\), donc on peut en mettre trois, quatre ou cinq en chaque sommet (ce qui conduit au tétraèdre, à l’octaèdre et à l’icosaèdre) ;
-
le carré avec un angle de \(90 °\), donc on peut en mettre trois au maximum (on reconnaît le cube) ;
-
le pentagone régulier avec un angle de \(108 °\), donc on peut en mettre trois au maximum également (on reconnaît le dodécaèdre).
À partir de l’hexagone régulier, les angles au sommet sont au moins égaux à \(120 °\).
Toute surface compacte est triangulable
Un théorème de Radó (1895-1965) affirme que toute surface topologique compacte admet une triangulation1[6] . D’autres démonstrations ont depuis été publiées dans la littérature, on peut par exemple citer celle de Doyle et Moran qui est relativement courte [5]. Très concrètement, cela signifie qu’il est toujours possible de découper la surface en un nombre fini de pièces triangulaires et donc, de manière imagée, de voir celle-ci comme un puzzle dont toutes les pièces seraient des triangles.
L’image ci-dessous du taureau, extraite du film Chaos [2], illustre ce théorème de triangulation. On remarque que sur les parties du corps du taureau ayant une faible courbure, on peut choisir les triangles relativement grands, alors que sur les parties très courbées (par exemple au voisinage des yeux ou dans les cornes), les triangles sont tout petits.

Si l’énoncé du théorème de triangulation est intuitivement clair, aucune démonstration ne peut véritablement être « facile ». Celle de Doyle et Moran tient en moins de trois pages mais s’appuie sur le théorème de Jordan-Schoenflies qui assure que toute courbe fermée simple sépare le plan en deux régions, l’une bornée, l’autre non, et qu’on peut toujours trouver un homéomorphisme du plan qui envoie une telle courbe sur le cercle unité. Là encore, si l’énoncé du théorème de Jordan-Schoenflies est intuitivement clair, il n’en demeure pas moins qu’il est loin d’être une évidence…
Donnons malgré tout quelques éléments de démonstration du fait que toute surface fermée 2 \(S\) admet une triangulation. Puisque \(S\) est compacte et localement homéomorphe au plan, on peut trouver un nombre fini de disques fermés dont la réunion recouvre \(S\). On peut également supposer qu’un tel recouvrement est irréductible, c’est-à-dire que si l’on retire l’un quelconque de ces disques, alors la réunion n’est plus égale à \(S\) ; en particulier, cela assure qu’aucun disque n’est entièrement contenu dans un autre disque et on écarte ainsi la présence éventuelle de région en forme d’anneau. Supposons à présent, et c’est le point délicat, que l’on puisse déformer les disques pour que leurs bords s’intersectent « gentiment », comme sur la partie gauche de la figure ci-dessous extraite de [4].
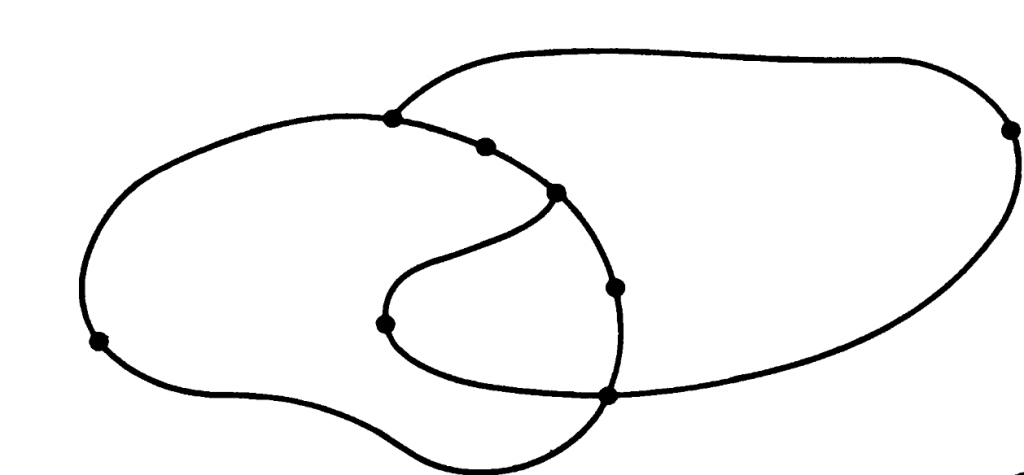

Plus précisément, après déformation, on suppose que l’intersection de deux disques se fait selon un nombre fini de points et un nombre fini d’arcs ; on introduit alors un sommet en chaque point où au moins trois arcs se rejoignent et au milieu de chaque arc. Finalement, dans chaque région dessinée par le nouveau recouvrement, on introduit un sommet en un point intérieur de la région (qui est topologiquement un disque), ce qui permet in fine de définir une triangulation de celle-ci (par une construction topologique analogue à celle qui permet de passer d’un polygone régulier à \(p\) côtés à \(p\) triangles isocèles), et donc de la surface elle-même comme l’illustre la partie droite de la figure.
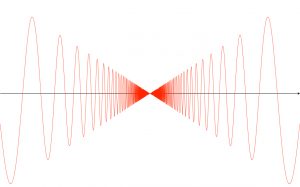
Pour convaincre le lecteur qu’il y a bien quelque chose de non trivial à démontrer au moment du point délicat mentionné ci-dessus, dessinons le graphe de la fonction \(x \longmapsto x \sin\left(\dfrac{1}{x}\right)\) au voisinage de \(0\), prolongée par \(0\) en \(0\). L’intersection de ce graphe avec l’axe des abscisses donne une idée de la complexité éventuelle de l’intersection de deux courbes fermées simples du plan…
Si toutes les surfaces fermées admettent une triangulation comme nous venons de le voir, certaines sont naturellement triangulées, comme le tétraèdre. Dans l’article [1] disponible en ligne, nous expliquons en détail comment préparer un fichier pour imprimer son propre tétraèdre. Après la théorie, place à la pratique pour les plus enthousiastes !
Références
- A. Alvarez. Triangulation et impression 3D. Version uniquement en ligne. Au fil des maths, 2019. ↩
- A. Alvarez, É. Ghys et J. Leys. Chaos, une aventure mathématique.
 . 2013. ↩
. 2013. ↩ - A. Alvarez, É. Ghys et J. Leys. Dimensions, une promenade mathématique.
 . 2008. ↩
. 2008. ↩ - M. A. Armstrong. Basic Topology. Springer, 1983. ↩
- D. A. Moran et P. H. Doyle. A Short Proof that Compact 2 -Manifolds Can Be Triangulated. vol. 5, p. 160-162. Inventiones
mathematicae, 1968. ↩ - T. Radó. Über den Begriff der Riemannschen Fläche. vol. 2, p. 101-121. Acts. Litt. Sci. Szeged., 1925. ↩
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Aurélien Alvarez est enseignant-chercheur à l’Institut Denis Poisson, le laboratoire de mathématiques des universités d’Orléans et de Tours, et formateur au centre national de la Fondation La main à la pâte. Il participe à de nombreux projets de diffusion de mathématiques et est le rédacteur en chef de la revue en ligne Image des mathématiques
.
-
-
-
De manière informelle, une triangulation d’une surface est une famille de points reliés par des arcs tracés sur la surface et disjoints deux à deux, de sorte que l’on découpe ainsi la surface en petits morceaux ressemblant beaucoup à des triangles du plan.↩
-
Une surface est dite fermée si et seulement si elle est compacte et sans bord.↩
-
-


Une réflexion sur « Triangulation et impression 3D »
Les commentaires sont fermés.