Comment j’ai dessiné certaines de mes planches

Vous allez découvrir dans ce numéro une nouvelle planche de BD d’Olivier Longuet. Avez-vous identifié toutes les subtilités de celle du 527 « Arrêtons le carrelage » ? Allez-vous reconnaître « La vie mode d’emploi » de Perec dans la planche ci-après ?
Olivier Longuet, adepte de l’OuBaPo, vous dévoile quelques secrets de fabrication¹.

Olivier Longuet

© APMEP Juin 2018

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

En 1960, l’écrivain Raymond Queneau et le mathématicien François Le Lionnais fondent l’OuLiPo, ouvroir de littérature potentielle, groupe de littéraires et de scientifiques qui se propose d’écrire des textes à partir de contraintes souvent mathématiques. Raymond Queneau énonce : « Nous appelons littérature potentielle la recherche de formes, de structures nouvelles et qui pourront être utilisées par les écrivains de la façon qu’il leur plaira ». Un oulipien aime à se décrire comme un rat qui construit lui-même le labyrinthe dont il se propose de sortir. Le côté ludique de leurs écrits apparaît par exemple dans le sous titre d’une de leurs anthologies : créations, re-créations, récréations.

Les contraintes, classées dans la table de Queneleiev, peuvent porter sur les constituants d’un texte (lettre, ponctuation, syllabe, mot, phrase, vers, chapitre) comme sur leur sens (personnage, lieu, action, sentiments, objets, durée).

Parmi les œuvres les plus célèbres créées au sein de l’OuLiPo, on peut citer Cent mille milliards de poèmes de Raymond Queneau, La disparition et La vie mode d’emploi de Georges Perec, Si par une nuit d’hiver un voyageur d’Italo Calvino, et de nombreux ouvrages collectifs.

Des exercices de textes à contraintes sont assez connus, comme le palindrome (une phrase qui peut se lire dans les deux sens, comme « engage le jeu que je le gagne »), le lipogramme (on s’interdit l’usage d’une lettre comme dans La disparition, roman privé de la lettre E), la méthode \(S + 7\) (substantif + 7 : dans un texte connu, on substitue chaque nom commun par le 7^e suivant dans un dictionnaire choisi ; par exemple, « la cimaise et la fraction » est un \(S + 7\) de « la cigale et la fourmi »). Le plus souvent, on peut associer chaque contrainte à une notion mathématique (la symétrie, la soustraction, l’addition dans les cas cités).

L’OuLiPo a de nombreuses petites sœurs, dans différents domaines, par exemple l’OuMuPo (ouvroir de musique potentielle), l’OuPeinPo (peinture), l’OuLiPoPo (littérature policière) ou encore l’OuBaPo (Bande dessinée). Dans tous ces domaines, on peut jouer avec tous les éléments de la grammaire du médium. Par exemple, dans l’OuBaPo, en plus du jeu sur le texte, on peut trouver des contraintes sur le dessin, sur les cases, sur les strips ou sur les planches, Certaines bandes de l’OuBaPo ont une inspiration mathématique certaine et assumée, en particulier les travaux d’Étienne Lécroart (Contes & Décomptes) ou de Jason Shiga (Vanille ou chocolat).

La vie mode d’emploi de Georges Perec, par sa structure utilisant un immeuble en coupe, peut presque être visualisé comme une grande planche de bande dessinée, et attire les auteurs de bande dessinée oubapienne ; un projet oubapien nommé « l’immeuble » est d’ailleurs évoqué depuis de nombreuses années, pas encore paru.

En tant que dessinateur amateur d’OuBaPo, j’ai voulu dessiner une planche présentant ce roman en utilisant les mêmes contraintes. Je vous présente ma démarche, en espérant qu’elle peut servir en tant qu’exemple de construction de labyrinthe. Chaque planche est une aventure, et celle-ci a été riche de recherches et de surprises combinatoires et esthétiques que je voudrais humblement partager.

Pour écrire ce livre, l’un de ses romans les plus ambitieux, Georges Perec, en bon oulipien, définit tout d’abord son cahier des charges, les contraintes qui vont structurer son roman : une centaine de chapitres décrivant chaque pièce d’un immeuble, chaque chapitre comportant deux mots parmi une liste disposés suivant un bi-carré latin orthogonal d’ordre 10 (ou un carré gréco-latin d’ordre \(10\)) et l’ordre des chapitres agencé par la course d’un cavalier sur un damier. Dans un carré gréco-latin d’ordre \(n\), on doit pouvoir placer des couples de lettres latines et grecques (\(n\) lettres latines et \(n\) lettres grecques) dans chaque ligne et chaque colonne de telle manière que chaque couple de lettres latine et grecque soit placé une fois et une seule dans le carré, et que chaque lettre latine ou grecque soit placée une fois par ligne et une fois par colonne.

Le problème de la polygraphie du cavalier, très connu des amateurs d’échecs, consiste à faire parcourir au cavalier toutes les cases d’un échiquier ou d’un damier une fois et une seule.

Ces deux problèmes étant associés à Léonhard Euler, j’ai imaginé une rencontre entre ces deux hommes, bien qu’ils n’aient pas vécu à la même époque. Euler avait essayé en vain de disposer \(36\) officiers (\(6\) grades différents de \(6\) régiments différents) dans un carré d’ordre \(6\) de telle manière qu’il y ait un seul officier de chaque grade et de chaque régiment sur chaque ligne et sur chaque colonne. Il conjecture qu’une telle disposition est impossible dans ce carré, puis qu’elle est aussi impossible pour un carré de côté \(n\), avec \(n\) congru à \(2\) modulo \(4\), c’est-à-dire pour un carré de côté \(10\) ou \(14\). En 1960, à l’aide d’ordinateurs, les chercheurs Bose, Parker et Shrikhande trouvent une solution pour le carré de côté \(10\), réfutant ainsi la conjecture d’Euler.

Pour dessiner la solution des \(100\) officiers, trouvée dans un document écrit par Perec, j’ai choisi un symbole pour chaque officier et une couleur pour chaque arme, ce qui m’a amené à représenter la solution sous la manière d’un jeu.

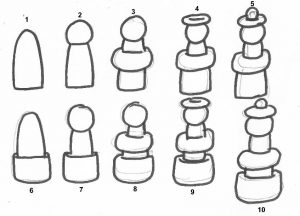
Ensuite, j’ai décidé d’organiser ma planche à la manière du roman, c’est-à-dire sous la forme d’un carré gréco-latin en me demandant comment la course du cavalier pourrait s’y dérouler. Pour dessiner les cases, j’ai dessiné un gaufrier (terme de bande dessinée désignant une répartition régulière en cases identiques, qui ressemble donc à une gaufre) de \(3 \times 3\) cases, car si j’avais choisi davantage de cases, \(4 \times 4\) par exemple, les cases auraient été plus petites et moins lisibles.

Pour organiser ce carré gréco-latin d’ordre \(3\), il fallait donc choisir \(6\) mots. Certains étaient évidents, au vu de la thématique (livre, officiers, cavalier), les trois autres étant davantage des éléments de décor (tasse, chat, fenêtre). Je me suis permis de faire figurer ces mots en les écrivant en toutes lettres ou en les dessinant, au choix, afin de rendre le décryptage un peu plus ludique. Chaque mot de la liste sera présent dans une seule case sur chaque ligne et sur chaque colonne. Le problème des \(9\) officiers admet une solution unique.

Aux permutations des lettres près, il existe deux manières de placer les \(3\) lettres dans ces deux cases.

Je vous invite à les retrouver sur une feuille de papier, le jeu est amusant et très facile.
En combinant les lettres latines et grecques, on obtient le carré gréco-latin d’ordre \(3\).
En prenant la correspondance :

on obtient la répartition de mes mots dans mes cases

J’ai choisi la première ligne, assez naturellement en me basant sur les mots dont j’avais le plus besoin pour définir l’histoire. Ensuite, placer les mots dans les bonnes cases a guidé la mise en scène de la planche et m’a donc aidé à sa conception.

La contrainte libère la créativité, comme aiment à le défendre les oulipiens, d’autant qu’en sachant que la règle du jeu est une partie de l’intérêt de la planche, on dessine assez rassuré sur son contenu, en se concentrant juste sur les détails.

Euler a étudié le problème de la polygraphie du cavalier et trouvé de multiples solutions sur l’échiquier et le damier [3] et Perec, amateur de jeux, a cherché aussi sa solution. Parmi les solutions d’Euler, les plus impressionnantes sont celles qui font un cycle, revenant sur la case de départ à la fin du parcours.

Les damiers ne sont pas tous parcourables par le cavalier : le damier \(3 \times 3\), en particulier, ne l’est pas, car il n’est pas possible d’atteindre la case centrale. Au sens de parcours près, il y a un cycle qui permet de relier toutes les autres cases et que je trouve très esthétique.

En suivant le parcours et en partant du mot Cavalier dans la case B3, on visite toutes les cases avec le mot Cavalier, avant d’arriver à la case Cavalier Chat, puis on visite toutes les cases du Chat, puis de même toutes les cases Fenêtre, puis toutes les cases Tasse. Les cases Livre et Officiers, dont la case centrale, ne sont pas prises en compte dans ce parcours mais sont liés à des mots opposés dans ce cycle, ce que j’ai représenté sur cette figure :

Au delà de cette constatation, j’aurais dans doute pu créer une seconde façon de lire la bande dessinée, en suivant le chemin du cavalier pour obtenir une autre progression logique des cases, une autre histoire, mais le ton imposé par l’histoire ne permettait sans doute pas de faire ce pas de côté.

Bibliographie

1. Marcel Bénabou et Paul Fournel, éd. Anthologie de l’OuLiPo. Paris : Gallimard, 2009.

2. Italo Calvino. Si par une nuit d’hiver un voyageur. Paris : Éditions du Seuil.

3. Leonhard Euler. « Solution d’une question curieuse qui ne paroit soumise à aucune analyse ». In : Mémoires de l’académie des sciences de Berlin no 15 (1766). .↩

4. Étienne Lécroart. Contes & Décomptes. . Paris : Édition l’Association, 2012.

5. OuBaPo. Oupus 1 à 6. L’Association.

6. OuLiPo. La littérature potentielle. Créations Re-création Récréations. Paris : Gallimard, 1973.

7. Georges Perec. La disparition. Paris : Gallimard, 1969.

8. Georges Perec. La vie mode d’emploi. Paris : Hachette.

9. Georges Perec. « Quatre figures pour La vie mode d’emploi ». In : L’Arc no 76 (1980).

10. Raymond Queneau. Cent mille milliards de poèmes. Paris : Gallimard.

11. Jason Shiga. Vanille ou chocolat. Paris : Cambourakis, 2012.

Olivier Longuet est enseignant de mathématiques au lycée Alain Chartier de Bayeux et membre de l’équipe d’Au fil des maths.