La preuve par 9
Les problèmes de Papy Michel

La « preuve par 9 », vous connaissez ? Elle a longtemps été enseignée en primaire et utilisée par les écoliers pour vérifier le produit de deux entiers. Selon votre scolarité, vous l’aurez systématiquement mise en œuvre… ou pas ! Cet article fait le point sur cette preuve qui porte plutôt mal son nom.

Michel Soufflet

© APMEP Décembre 2019

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

La technique

Ce que plusieurs générations d’écoliers ont fait, mécaniquement, sans trop savoir comment et pourquoi ça marchait…
Après avoir calculé le produit de deux entiers \(\mathsf{A}\) et \(\mathsf{B}\), on dessine une croix en forme de \(\times\) (le signe de la multiplication) délimitant quatre parties dans laquelle on reporte quatre entiers \(a\), \(b\), \(c\) et \(d\) compris entre 0 et 9.

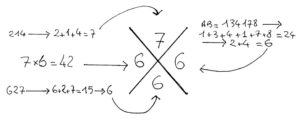
Un exemple avec le produit \(\mathsf{A}\times\mathsf{B}= 214\times627\).
\(a\) est la somme réduite des chiffres de \(\mathsf{A}\), elle s’obtient en additionnant tous les chiffres de l’entier \(\mathsf{A}\).
Ici \(a=2+1+4=7\).
\(b\) est la somme réduite des chiffres de \(\mathsf{B}\).
Ici, \(\mathsf{B}=627\) et \(6+2+7=15\geqslant9\) donc on poursuit « la réduction » : \(1+5=6\) pour trouver finalement \(b=6\).
Si le total est égal à 9, il est remplacé par 0.
On procède à la somme des chiffres jusqu’à l’obtention d’un nombre à un seul chiffre.
\(c\) est la somme réduite du produit \(ab\). Ici \(ab=42\), donc \(c=4+2=6\).
Enfin, \(d\) est la somme réduite du produit obtenu \(\mathsf{AB}\).
Ici, si nous avons trouvé \(\mathsf{AB}=134\;178\), alors \(d=6\).

L’opération est considérée comme juste lorsque \(c\) et \(d\) sont égaux.

On ne savait pas pourquoi ça marchait mais c’était facile à réaliser et quelquefois exigé de l’enseignant.

Comment ça marche ?

Essayons de comprendre, imaginons que nous avons 10 billes à répartir entre 9 enfants, la distribution faite, il va nous en rester une.
Si nous en distribuons 20, il va en rester 2.
Si nous en distribuons 70, il va en rester 7.
Si nous en distribuons 100, il va en rester 1.
Si nous en distribuons 500, il va en rester 5…
Si maintenant nous avons 572 billes à distribuer, puisque 572 = 500+70+2, il va en rester 5+7+2 = 14, soit, avec un tour de plus, 5.

Ce que l’on observe, c’est que le reste dans la division de A par 9 est sa forme réduite.

Cette observation ne se limite pas aux entiers à trois chiffres : puisque 1000 = 999+1 et que 4765 = 4000+700+60+5, si nous distribuons 4765 billes, il en restera 4+7+6+5 = 22, et puisque 22 = 20+2, il en restera 2+2, soit 4 billes.

Vous me direz, ce n’est pas une démonstration ; un cas particulier ne saurait démontrer le général. Certes, mais quand le particulier est lui-même général ? Si notre observation ne démontre pas, elle permet de se convaincre de la généralité de la propriété.

Puisque le reste de toute puissance de 10 dans la division par 9 est 1, cette propriété se généralise facilement et permet de comprendre le « pourquoi » de la règle de divisibilité par 9.

Expérimentée dans les classes de CM2, cette activité ludique peut se faire lorsque l’on étudie la règle de divisibilité par 9. Elle est plaisante et peut donner l’envie aux enfants de faire des mathématiques. L’arithmétique étant, avec la géométrie, un domaine propice à susciter des vocations.

Pour justifier la « preuve par 9 », il faut maintenant établir que le produit AB a le même reste que le produit ab dans la division par 9.

Si A = 9q+a avec a < 9, et B = 9q’+b avec b<9, alors AB = (9q+a)(9q’+b) = 9(9qq’+aq’+bq)+ab.

Le produit ab n’est peut être pas le reste de AB dans la division par 9, mais ab et AB ont le même reste dans cette division.

Qu’a-t-on prouvé au fait ?

On a prouvé que si la « preuve par 9 » n’est pas vérifiée, alors le produit obtenu est faux.

Si la « preuve par 9 » est vérifiée, cela prouve seulement que nous avons le bon résultat à un multiple de 9 près.

Mais un élève qui combinera plusieurs erreurs de calculs pourra penser, à tort, que son produit est juste… et il faudra reprendre avec lui les calculs intermédiaires. Cette preuve ne révélera pas non plus les étourderies simples comme la permutation de deux chiffres en recopiant le résultat ; ces fautes étant très courantes surtout chez les élèves atteint de légère dyslexie, elle n’apportait guère de sécurité. Lorsque j’étais écolier, je ne la pratiquais que lorsqu’elle était demandée !

Eh oui, cette preuve porte bien mal son nom !

Je vous parle d’un temps
Que les moins d’cinquante ans
Ne peuvent pas connaître !
(d’après Charles Aznavour, « La Bohème »)

NDLR

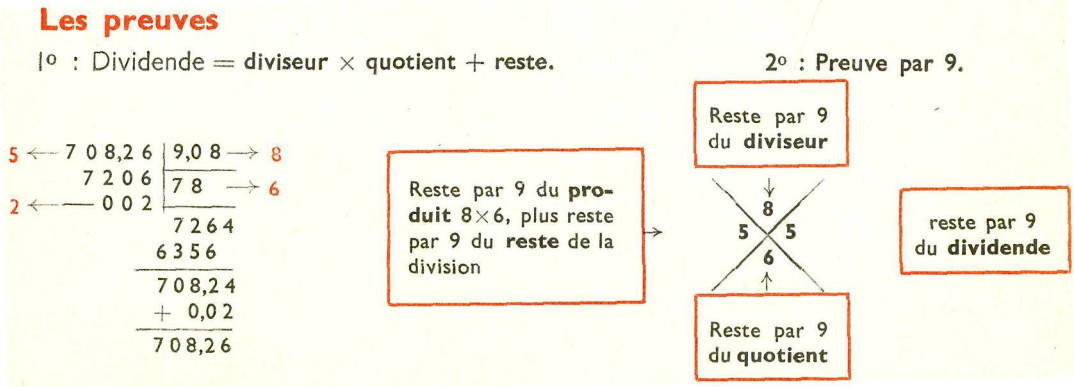
À partir de la classe de Troisième, on peut espérer faire comprendre aux élèves ce que cette « preuve » permet réellement de justifier. La maîtrise de la double distributivité étant une attente de la fin du cycle 4, on peut envisager de diffuser aux élèves un extrait du manuel Calcul Vivant et de les faire réfléchir sur la technique puis sur ce qui a été prouvé. Les petits curieux ne manqueront pas de s’interroger sur la possibilité d’une preuve par d’autres nombres que 9 et de son utilisation pour les autres opérations… Le nouveau programme de mathématiques expertes (applicable en terminale générale dès la rentrée 2020 pour les élèves qui choisiront cet enseignement) prévoit une partie arithmétique fournie. Il précise qu’ une place importante sera faite à l’étude des congruences (arithmétique modulaire). De quoi envisager une activité autour de cette « preuve » !

Ressources

1. Gérard Villemin
2. Images des maths (CNRS)

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Michel Soufflet, professeur retraité, a été président de l’APMEP et animateur IREM de Basse Normandie.