La méthode des coordonnées de Descartes

Martine Bühler

© APMEP Décembre 2020

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Les programmes de mathématiques du lycée de la rentrée 2019 font la part belle à l’histoire des mathématiques et recommande la lecture de textes originaux. On y trouve, pour la partie « Géométrie » en Seconde : « Les progrès apportés par la « méthode des coordonnées » de Descartes […] permettent de relier efficacement géométrie, physique et calcul ». La rédaction d’un programme, obligatoirement succincte, peut laisser croire à un développement linéaire des mathématiques, avec, de temps à autre, une innovation importante de la part d’un personnage isolé. La réalité est plus complexe et, pour mieux l’appréhender, on peut se plonger dans la lecture de textes originaux.

Descartes publie en 1637 son Discours de la Méthode pour bien conduire sa raison et chercher la vérité dans les sciences, accompagné de trois essais, La Dioptrique, Les Météores et La Géométrie. Ce dernier texte commence par présenter une méthode : l’arithmétisation de la géométrie, étendant les opérations arithmétiques aux « lignes droites »¹, qui ouvre de nouvelles perspectives pour la résolution de problèmes de géométrie, en les ramenant à la résolution d’équations, et donne des constructions géométriques permettant de résoudre des équations. Le livre I se termine par la résolution d’un problème (dit « de Pappus ») de construction géométrique « que ni Euclide, ni Apollonius, ni les autres n’avaient su entièrement résoudre », comme illustration de la force de sa méthode. Le livre II commence par des considérations sur la nature des lignes courbes, et c’est là qu’on trouve la notion d’équation d’une courbe. Descartes donne ensuite une méthode générale pour déterminer les normales (et donc les tangentes) à une courbe en un point donné de la courbe. Le style de Descartes est souvent elliptique, et des textes ultérieurs sont parfois plus éclairants sur les idées de Descartes. Nous essaierons de montrer comment la notion de coordonnées a émergé au cours de l’histoire et nous nous intéresserons à la « méthode des coordonnées » de Descartes.

Voici ce qu’en dit Charles-René Reyneau (1656–1728) dans Analyse démontrée ou la Méthode de résoudre les Problèmes de mathématiques et d’apprendre facilement ces sciences publiée en 1708 :

« On s’avisa heureusement dans le dernier siècle d’exprimer les lignes & les figures par les caractères familiers de l’alphabet, & de réduire ces expressions à un calcul facile, qui exprimât aussi tous les rapports simples & composés que peuvent avoir ces lignes & ces figures. On forma un Art méthodique (qui est ce que l’on nomme l’Analyse) pour trouver, par les rapports connus qu’ont les grandeurs inconnues que l’on cherche dans les Problèmes avec celles qui sont connues, des équations qui exprimassent les conditions & la nature, pour ainsi dire, des Problèmes ; et pour découvrir les valeurs des grandeurs inconnues de ces équations ; ce qui donne la résolution des Problèmes. Monsieur Descartes perfectionna et réduisit à une extrême facilité ces calculs et cette Analyse naissante. Il y ajouta l’excellente […] méthode de réduire les lignes courbes à des équations qui en exprimassent les principales propriétés & de tirer de ces équations toutes les choses que l’on pouvait désirer connaître sur ces courbes ; enfin la manière d’employer les courbes elles-mêmes à la résolution des équations & des problèmes. On vit une Géométrie nouvelle, qui contenait tout ce que nous avions reçu des Anciens, & qui allait infiniment plus loin : les résolutions étaient générales, & aucun cas particulier ne leur échappait. »

La recherche d’une méthode générale pour résoudre les problèmes, voilà effectivement le but de Descartes, et d’autres mathématiciens du xvii siècle. Mais ces équations dont parle Reyneau mettent-elles en jeu ce que nous appelons « coordonnées cartésiennes » ? Voici un extrait de l’article « courbe » de L’Encyclopédie méthodique de Diderot et d’Alembert (1784–1789) :

« Descartes est le premier qui ait pensé à exprimer les lignes courbes par des équations.

Cette idée sur laquelle est fondée l’application de l’Algèbre à la Géométrie est très heureuse et très féconde.

[…] il faut considérer d’abord la manière dont on détermine la nature d’une ligne courbe.

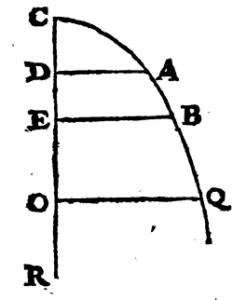
On rapporte les points de cette courbe \(\mathsf{CABQ}\) par des lignes \(\mathsf{AD}\), \(\mathsf{BE}\), \(\mathsf{QO}\), qu’on appelle ordonnées, à une ligne droite fixe & indéfinie \(\mathsf{CR}\) tirée dans le plan de la courbe, & sur laquelle ces lignes \(\mathsf{AD}\), \(\mathsf{BE}\), \(\mathsf{QO}\) sont perpendiculaires ; les parties \(\mathsf{CD}\), \(\mathsf{CE}\), \(\mathsf{CO}\) de la ligne \(\mathsf{CR}\), s’appellent les abscisses.

On sent bien que puisque la nature de la courbe \(\mathsf{CABQ}\) est déterminée, la longueur de chaque ordonnée \(\mathsf{DA}\) doit être déterminée par rapport à l’abscisse correspondante \(\mathsf{CD}\), puisque c’est la longueur plus ou moins grande de cette ordonnée qui donne par son extrémité le point correspondant \(\mathsf{A}\) de la courbe. La nature de la courbe consiste donc dans un certain rapport, une certaine loi qui s’observe entre chaque ordonnée comme \(\mathsf{DA}\), & l’abscisse \(\mathsf{CD}\) correspondante. »

Ainsi, l’on voit que les « coordonnées » ne sont pas des nombres, mais des « lignes », et qu’un seul « axe » est défini². Il faudra du temps avant qu’on ne passe aux nombres pour les coordonnées, et cela se fera progressivement. Voici ce qu’écrit Gabriel Cramer (1704–1752) dans son Introduction à l’Analyse des lignes courbes algébriques, publiée en 1750 :

« Descartes est le premier, je pense, qui ait entrepris d’exprimer la nature des Lignes par des Équations algébriques. Voici comment il s’y est pris.

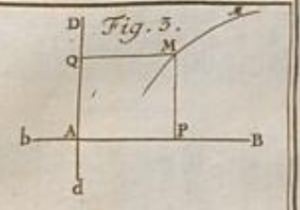
Dans le plan, sur lequel une Ligne comme \(\mathsf{M}\mathscr{M}\) est tracée, on choisit à volonté un Point fixe, qu’on nomme l’Origine, par lequel on mène à discrétion deux Droites \(\mathsf{AB}\), \(\mathsf{AD}\). De chaque point \(\mathsf{M}\) de la Ligne \(\mathsf{M}\mathscr{M}\) on mène des Droites \(\mathsf{MP}\), \(\mathsf{MQ}\) parallèles aux Droites \(\mathsf{AB}\), \(\mathsf{AD}\) et qui y sont terminées réciproquement. L’une, comme \(\mathsf{MP}\) ou son égale \(\mathsf{AQ}\), se nomme l’Ordonnée ou l’Appliquée. L’autre, comme \(\mathsf{MQ}\) ou son égale \(\mathsf{AP}\), se nomme la Coupée ou l’Abscisse. C’est pourquoi la Droite \(\mathsf{AB}\) s’appelle la Ligne ou l’Axe des abscisses ou des coupées, et la droite \(\mathsf{AD}\) la Ligne ou l’Axe des ordonnées ou des appliquées. Et l’on se sert du mot de coordonnées pour exprimer en commun l’abscisse & l’ordonnée d’un même point. »

On voit apparaître les deux axes de coordonnées, mais toujours des lignes pour les coordonnées. On trouve chez Euler (1707–1783) des conceptions plus proches des nôtres (mais un seul axe) dans le second tome de son Introductio in analysin infinitorum publiée en 1748 :

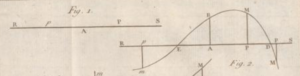
« Il faut donc, avant tout, fixer sur une droite indéfinie \(\mathsf{RS}\) un point \(\mathsf{A}\) qui sera censé l’origine des grandeurs déterminées […]. Une portion déterminée \(\mathsf{AP}\) représentera une grandeur déterminée […]

Soit donc \(x\) une quantité variable, représentée par la droite indéfinie \(\mathsf{RS}\) ; il est clair que toutes les valeurs déterminées de \(x\), pourvu qu’elles soient réelles, peuvent être exprimées par des portions prises sur la droite \(\mathsf{RS}\). […]

Si nous prenons les valeurs positives de \(x\) en allant sur la droite depuis le point \(\mathsf{A}\), les intervalles \(\mathsf{Ap}\) situés sur la gauche représenteront les valeurs négatives de \(x\).

Cherchons à présent une manière très commode de représenter géométriquement une fonction quelconque de \(x\). Soit \(y\) cette fonction de \(x\) […] Ayant pris une droite indéfinie \(\mathsf{RAS}\) pour représenter les valeurs de \(x\), il faudra, pour chaque valeur \(\mathsf{AP}\) déterminée de \(x\), élever sur cette ligne une perpendiculaire \(\mathsf{PM}\), égale à la valeur correspondante de \(y\) ; c’est-à-dire que si la valeur de \(y\) est positive, il faudra la placer au-dessus de \(\mathsf{RS}\) ; mais si la valeur de \(y\) devient négative, il faudra la placer perpendiculairement au-dessous de \(\mathsf{RS}\). »

Euler a donné dans le tome premier la définition de « quantité variable » :

« […] Une quantité variable est une quantité indéterminée, ou, si l’on veut, une quantité universelle, qui comprend toutes les valeurs déterminées.

Une valeur déterminée quelconque pouvant être exprimée en nombre, il s’ensuit qu’une quantité variable comprend tous les nombres de quelque nature qu’ils soient. […] »

On voit ainsi, à travers ces textes, la notion de « coordonnées » s’installer peu à peu, assez différente au départ de notre perception actuelle, avec des conceptions différentes co-existant à la même époque. Ainsi, les « coordonnées » restent pendant longtemps des lignes et pas des nombres ; on s’appuie sur un axe et une direction plutôt que sur deux axes. Cet article ne peut évidemment pas être exhaustif et il serait intéressant de voir comment certains prennent en compte des « quantités négatives », ce que ne fait pas Descartes. Si on ne peut dénier à La Géométrie son caractère novateur, il faut cependant être conscient que d’autres mathématiciens, contemporains de Descartes, pouvaient avoir des idées similaires, s’appuyant sur des travaux plus anciens. C’est en particulier le cas de Fermat.

Compléments historiques et idées pour la classe

Vous trouverez dans la brochure³ 79 du groupe M.:A.T.H. un résumé sur la vie et l’œuvre de Descartes ainsi que des exercices utilisables en Troisième et Seconde (pp. 115-119) utilisant des extraits de La Géométrie, pour montrer « comment le calcul d’Arithmétique se rapporte aux opérations de géométrie », des exercices plutôt pour la spécialité en Première sur l’insertion de moyennes proportionnelles (pp. 120-122) et la construction géométrique de solutions d’équations du second degré (pp. 123-125).

D’autre part, des extraits de La Géométrie de Descartes sont recensés dans un document disponible sur le site du groupe M.:ATH de l’IREM de Paris (paragraphe « Autour de la Géométrie de Descartes »). Nous incitons le lecteur à aller consulter cette page car on y trouve une version actualisée de deux exercices de la brochure 79 précédée de compléments historiques permettant de mieux comprendre les apports de Descartes, ainsi que des commentaires éclairants de Rabuel écrits un siècle après la parution de La Géométrie.

Références

1. Évelyne Barbin. « L’arithmétisation des grandeurs ». In : Repères-IREM n° 68 (2007). Paris. Disponible en ligne : , pp. 5-20.

2. Évelyne Barbin. « Pourquoi les contemporains de Descartes n’ont-ils pas compris sa Géométrie de 1637? » In : Circulation, Transmission, Héritage (2011). Université de Basse-Normandie, IREM de Basse Normandie. Caen.
3. Dominique Tournès. « Constructions d’équations algébriques ». In : Repères-IREM n° 59 (2005). Paris. Disponible en ligne : .
4. René Descartes. La Géométrie. Textes choisis et commentés
   par André Délédicq. Paris : ACL-Les Éditions du Kangourou, 2009.
5. René Descartes. Discours de la Méthode. Texte complet du Discours de la Méthode, y compris La Géométrie. Disponible en ligne sur Gallica : .

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Martine Bühler a enseigné les mathématiques au lycée Flora Tristan (Seine-Saint-Denis) ; elle est membre du groupe d’histoire des mathématiques de l’APMEP, et travaille au sein du groupe M.:A.T.H. de l’IREM Paris-Diderot. Ce groupe a été fondé au début des années 1980 par Jean-Luc Verley, alors enseignant à Paris VII, avec comme objectif l’introduction d’une perspective historique dans l’enseignement des mathématiques en s’appuyant sur les textes historiques. Le groupe a publié des brochures et une revue (Mnemosyne) à l’IREM, et anime régulièrement des stages de formation continue dans les académies d’Île-de-France. Le groupe anime également des séances mensuelles de lectures de textes historiques, dont le thème était, en 2018–2019, La Géométrie de Descartes.