Le pourquoi et le comment
Dans cette opinion sur la relation entre arts et mathématiques, Bernard Parzysz montre comment les mathématiques peuvent être source d’exploration et de création artistique, facilitant la compréhension des œuvres, tout en laissant une part au mystère et à l’inexplicable.
Bernard Parzysz
© APMEP Septembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Nous le savons, les mathématiques sont à même de nous fournir des grilles de lecture nous permettant de mieux comprendre le monde qui nous entoure, de découvrir « les choses qui sont cachées derrière les choses », comme le fait dire Jacques Prévert au peintre de Quai des Brumes (Marcel Carné, 1938). C’est également vrai en ce qui concerne l’art, et mes incursions — ou devrais-je dire excursions ? — dans des domaines variés qui lui sont liés m’ont maintes fois permis de le vérifier et de découvrir ainsi des richesses insoupçonnées. Mes échanges avec des spécialistes (musiciens, peintres, architectes, archéologues…) m’ont également convaincu qu’un bagage scientifique relativement modeste peut être un moyen de communication efficace entre des domaines différents et procurer à chacune des parties une vision à la fois plus étendue et plus profonde d’une œuvre, en nous mettant à même d’approcher — même si ce n’est que de façon partielle et incomplète — ses « pourquoi » et ses « comment ».
Il m’est tout d’abord apparu que, dans quelque domaine que ce soit, réaliser une œuvre d’art implique de satisfaire à des règles, liées au genre d’œuvre que l’on veut créer : une fugue, un sonnet ou un haïku obéissent à des principes de composition, un tableau repose sur une organisation de sa surface, le bois et la pierre ne se laissent pas sculpter n’importe comment, etc. C’est ainsi qu’André Gide a pu écrire que « l’art naît de contraintes », et le styliste Christian Lacroix préciser que « dans l’art, la contrainte est un instrument pour aller plus loin ». C’est d’ailleurs en poussant cette idée à l’extrême qu’a été créé l’Ouvroir de Littérature Potentielle (OuLiPo), au sein duquel a notamment œuvré Georges Perec1. C’est à l’OuLiPo que Jean Lescure a inventé la méthode d’écriture « S + 7 », où dans un texte on remplace chaque substantif par le septième qui le suit dans un dictionnaire donné, méthode qui nous évoque bien sûr la notion de translation ; c’est là aussi que Raymond Queneau a eu l’idée de son livre Cent mille milliards de poèmes [1], dont le titre s’explique grâce à la combinatoire d’une structure arborescente. Dans ces contraintes, les outils mathématiques ont souvent un rôle à jouer, en permettant d’accéder aux principes sousjacents — mais implicites — régissant l’œuvre, à leur fonctionnement (le « comment »), et même, parfois, à leur raison d’être (le « pourquoi »). À l’appui de mon propos, je prendrai maintenant trois petits exemples vécus.
En musique, d’abord
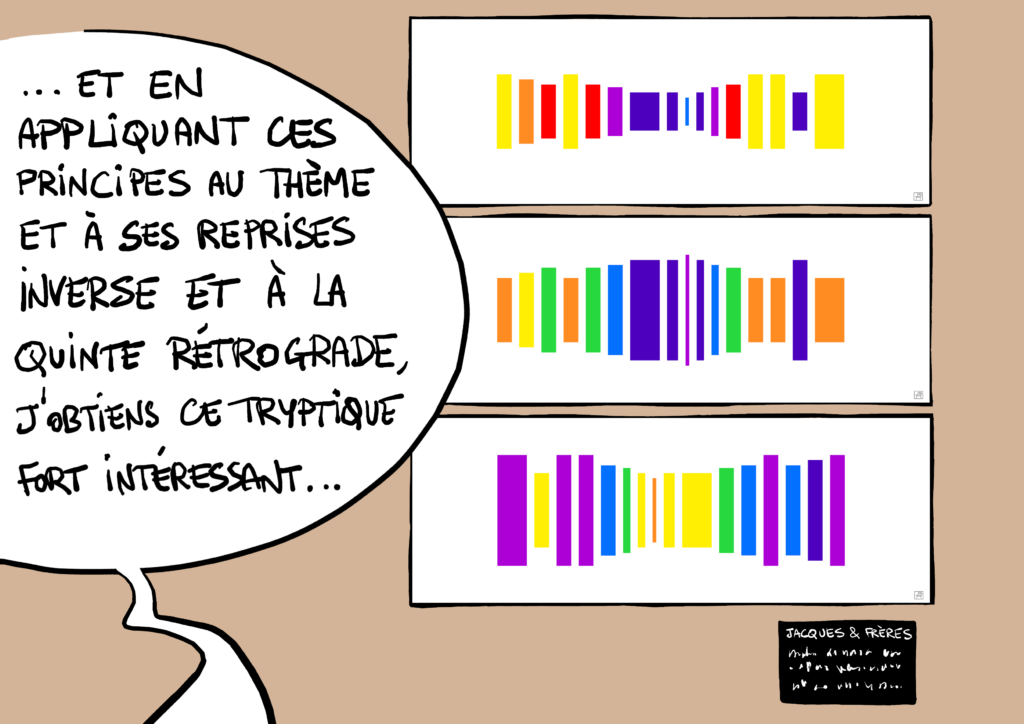
Dans une fugue, une même petite phrase mélodique (le sujet), se fait entendre tout le long de l’œuvre. Lorsqu’elle est reprise à l’unisson ou à l’octave elle reste inchangée, mais lorsqu’elle est reprise à la quinte elle est légèrement modifiée. Pourquoi ? Ici apparaissent la notion de tonalité (sous-ensemble de 7 notes parmi les 12 de l’échelle), celle de tonalités voisines (parties d’intersection maximale), et tout s’explique. Il arrive aussi que le sujet soit « renversé » (les intervalles conservent la même amplitude, mais les intervalles montants deviennent descendants et inversement) ; il arrive même qu’il devienne « rétrograde » (énoncé à l’envers, de la dernière à la première note), et on peut même combiner ces deux modifications en un renversement rétrograde [2]. On aura reconnu, avec ces quatre formes, un groupe isomorphe au « groupe du matelas », celui des symétries du rectangle2. À l’écoute d’une œuvre de Bach, par exemple, attendre et repérer les diverses apparitions du sujet sous diverses formes procure assurément un sentiment de connivence avec le compositeur, et on ne sait ce qu’il faut admirer le plus, ou le résultat, ou la façon dont Bach a procédé pour l’obtenir. On se rend alors compte que son génie s’appuie sur une connaissance approfondie des règles de la tonalité et du contrepoint.

En architecture ensuite
On sait que les amphithéâtres romains sont — dit-on couramment — « de forme elliptique » [3], et que la construction de l’ellipse par la « méthode du jardinier » remonte à Apollonius3. Rien n’empêche donc de penser que les amphithéâtres sont effectivement elliptiques… sauf si on entreprend d’en construire un. Pourquoi ? Parce que tout autour de l’arène se situe la cavea, zone de gradins où viendront s’asseoir les spectateurs. Or, tracer différentes rangées de gradins avec des ellipses de mêmes foyers conduit à créer un espace plus large vers les extrémités du grand axe, et plus étroit vers les extrémités du petit axe. Si on veut avoir le même confort sur tout le pourtour — comme on peut effectivement le constater sur place —, on va être contraint de changer la position des foyers pour chaque rangée. Et ici on peut imaginer qu’un architecte romain a eu un jour une illumination4. Laquelle ? Celle de substituer aux ellipses des ovales à quatre centres.
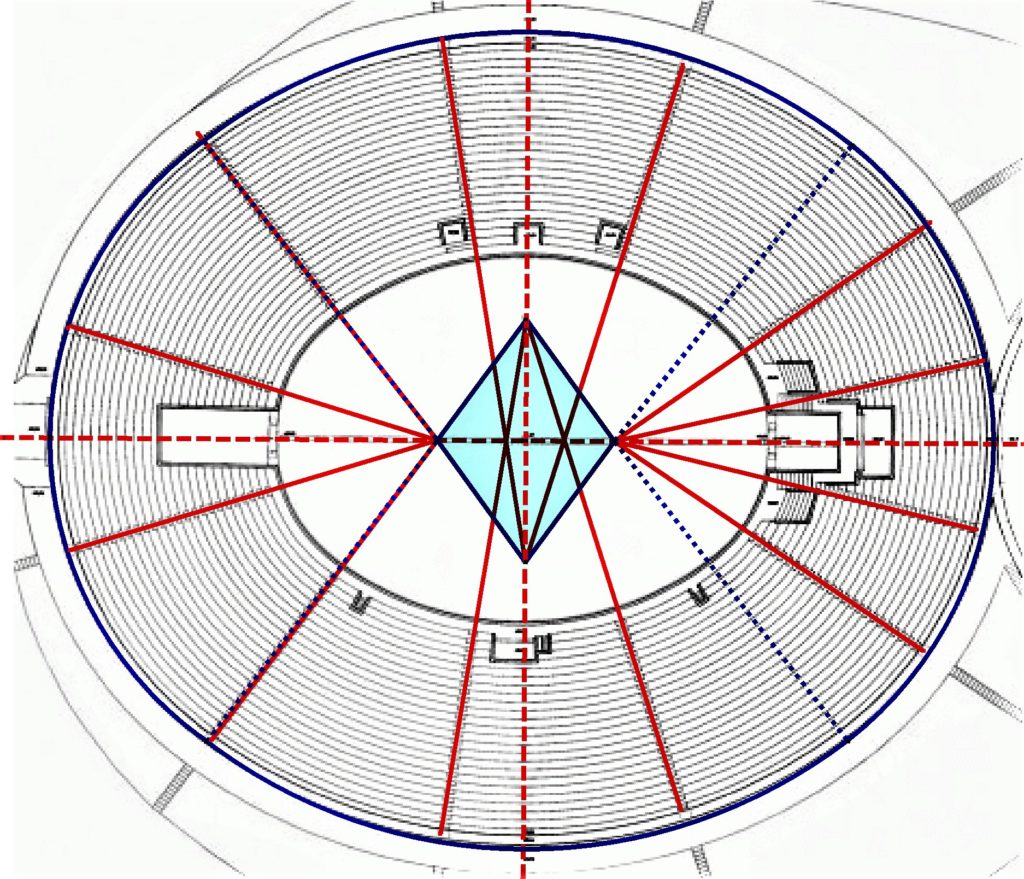
Ainsi, sans modifier la position des centres, on pouvait obtenir toute une famille de courbes équidistantes. Et du coup le problème géométrique était résolu de façon élégante, uniquement grâce à des tracés de cercles. Cerise sur la gâteau : l‘ovale de l’amphithéâtre est pratiquement indiscernable de l’ellipse de mêmes sommets [4].
Dans le domaine des arts décoratifs enfin
Je me suis notamment intéressé à la mosaïque d’époque romaine à décor dit « géométrique ». Selon Wikipedia, « la distinction entre art décoratif et bel art est surtout fondée sur la fonctionnalité, les intentions, l’importance, le statut d’œuvre unique ou de production liée à un seul artiste » [5]. Pour un pavement de mosaïque, la fonctionnalité est indubitable : il est fait pour qu’on marche dessus et fournit un sol résistant facile à nettoyer, les intentions sont de faire voir l’opulence du commanditaire, l’importance résulte du fait que seules les pièces d’apparat en étaient revêtues, le statut d’œuvre unique va de soi et l’artiste (le pictor) conçoit le décor, prépare et supervise le travail de la petite équipe qui posera le pavement. Le même article de Wikipedia précise que « ce champ inclut tous les artisanats de l’architecture d’intérieur et de la décoration d’intérieur », ce qui est bien en accord avec la mosaïque.
J’ai eu récemment l’opportunité d’étudier la totalité des pavements mosaïqués d’une villa romaine de la seconde moitié du IVe siècle située à Rabaçal, près de Coimbra au Portugal [6], ce qui m’a permis d’effectuer un travail extensif sur un ensemble décoratif complet et cohérent, et de confronter mes hypothèses antérieures à de nouveaux exemples. Une particularité du décor de cette villa m’a notamment frappé : l’omniprésence de l’élément décoratif appelé « tresse ». L’abondance des tresses à deux, trois, quatre ou cinq brins a ainsi été pour moi l’occasion d’entreprendre une étude approfondie de leur composition et de leur mise en place.
Dans la mosaïque romaine, la tresse sert essentiellement de bordure de séparation entre différents panneaux, et à ce titre elle est perçue par les archéologues spécialistes du décor comme un élément banal et sans grand intérêt. C’est pourtant un motif qui vaut la peine qu’on s’y attarde, car c’est l’un des lieux où l’on voit le mieux le travail du maître mosaïste, que ce soit dans la façon dont la tresse est mise en place à partir de tesselles5 isolées disposées très régulièrement en quinconce, la gestion des différents brins dans les bifurcations et les croisements, le camouflage des brins « orphelins » dans des endroits discrets, la répartition des différentes couleurs ou l’organisation générale de la surface. Celles de Rabaçal m’ont assurément passionné et j’y ai trouvé des réponses à beaucoup de « comment » que je me posais à propos de la mosaïque, même si je ne sais toujours pas pourquoi il y a tant de tresses dans le décor de cette villa ; peut-être s’agissait-il d’une spécialisation du mosaïste, ou d’un symbole, ou d’une fixation du propriétaire ?

Bien sûr, s’efforcer de comprendre comment une œuvre artistique a été réalisée est insuffisant à dire pourquoi elle est belle, mais cela montre au moins qu’elle est le résultat d’un travail et d’une recherche : « le génie ne fait rien que d’apprendre d’abord à poser des pierres, ensuite à bâtir, que de chercher toujours des matériaux et de travailler toujours à y mettre la forme » [7]. Et, comme le chantait naguère Georges Brassens, « sans technique un don n’est rien qu’une sal’ manie » [8].
J’espère avoir pu montrer, sur ces exemples, que les mathématiques constituent une voie particulièrement intéressante d’exploration, dans le domaine artistique comme dans bien d’autres. C’est pourquoi je plaide depuis longtemps pour une ouverture aussi large que possible de l’enseignement de notre discipline à des domaines d’application variés, par exemple en utilisant l’étude d’œuvres d’art comme source de problèmes. Certains élèves s’apercevront alors peut-être que la géométrie, l’algèbre, l’analyse, la statistique et les probabilités6 peuvent s’avérer des outils efficaces si l’on ne veut pas se contenter de rester seulement à la surface des choses, et ils pourront même avoir envie d’aller au-delà en fréquentant les lieux où l’art se donne à voir. Les collègues des autres disciplines ont bien évidemment un rôle incontournable à jouer dans cette démarche, aussi bien pour apporter leur point de vue que pour prévenir d’éventuelles dérives. Et je suis convaincu qu’ainsi tout le monde aurait à y gagner.
Référence
-
- Raymond Queneau. Cent mille milliards de poèmes. Réédité en septembre 2006. Gallimard, juillet 1961. ISBN : 2-07-010467-2.
-
- Bernard Parzysz. « Musique et transformations. Analyse d’une œuvre contemporaine ». In : Bulletin de l’APMEP 509 (2014), pp. 295-308.
-
- Amphithéâtre romain. Wikipedia.
-
- Bernard Parzysz. « Des ellipses… sans ellipses : les amphithéâtres romains ». In : Bulletin de l’APMEP 479 (2008), pp. 772-780.
-
- Arts décoratifs. Wikipédia.
-
- Bernard Parzysz et Miguel Pessoa. Les mosaïques de la villa romaine de Rabaçal. Formes et couleurs. Parcours géométrique. Penela (Portugal) : Direction générale du Patrimoine, 2019.
-
- Friedrich Nietzsche. Humain, top humain. aphorisme 192. Chap. IV.
- Georges Brassens. Le mauvais sujet repenti. Paris : Éditions Ray Ventura, 1955.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Bernard Parzysz est professeur émérite de l’université d’Orléans, membre du LDAR (Laboratoire de Didactique André Revuz) de l’université Paris-Diderot, et animateur à l’IREM de Paris-Diderot. Il collabore avec fidélité aux publications de l’APMEP.
![]()
-
-
Par exemple, son roman La disparition (1969, Gallimard) n’utilise jamais la voyelle e, et son autre roman Les Revenentes (1972, Julliard) n’utilise au contraire que cette seule voyelle.↩
-
-
-
Encore appelé groupe de Klein.↩
-
-
-
Proposition 52 du livre III des Coniques.↩
-
-
-
Travaux de J.-C. Golvin,↩
-
-
-
Les petits éléments de pierre, de verre ou de céramique qui constituent la mosaïque.↩
-
-
J’ai effectivement été amené à les utiliser tour à tour lors de mes « incursions » dans les domaines artistiques.↩

2 réflexions sur « Le pourquoi et le comment »
Les commentaires sont fermés.