Se coller aux « Khôlles »

Serge Radeff nous fait part de son expérience et de ses réflexions sur les « khôlles » auxquelles il a dû se coller que ce soit d’un côté ou de l’autre du tableau .

Serge Radeff

© APMEP Mars 2021

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

The name of the game

Le mot en lui-même laisse rêveur : «colles» voire «khôlles» ; les orthographes varient d’un lycée à un autre . «Khôlle», qui comme «khâgne» est d’origine grecque, donne une couleur plus mystérieuse voire secrète à cet exercice traditionnel des classes préparatoires et il permet sans doute aux anciens étudiants d’impressionner les nouveaux entrants . «Colle» semble plus banal et fait penser à une retenue du mercredi pour collégien remuant . Il y a du vrai là dedans, puisque la colle a souvent lieu le mercredi, mais celle-ci s’adresse pourtant à tous les étudiants … sages ou pas !

En tout cas, il semble bien que ce soient les élèves eux-mêmes qui aient inventé ce mot «colle» . Pour le Littré:

Colle : terme d’écolier ou plutôt d’aspirant à une école spéciale . Professeur ou maître de colles, examinateur qui vient à certains jours faire aux aspirants des questions difficiles et auxquelles ils ne sont pas préparés, afin qu’ils apprennent à y répondre .

Ce maître de colles est à son tour appelé colleur . Toujours dans le Littré, on trouve :

Colleur : dans l’argot des collèges, maître qui vient non pour faire des cours, mais pour interroger les élèves qui vont passer des examens et se destinent aux écoles spéciales, et pour les préparer en leur posant des questions difficiles .

Cette définition [1] est toujours valable de nos jours .

La colle (en 2020) est essentiellement une interrogation des étudiants (des «aspirants») qui se préparent à un concours aux écoles d’ingénieurs ou de commerce .

Mais avant de parler de l’époque actuelle et de rentrer dans les détails, restons un peu dans l’histoire et laissons la parole à Bruno Belhoste¹ qui, dans un article sur l’histoire de l’éducation, répond parfaitement à la question.

À l’origine qu’est-ce qu’une « colle » ?

«Ce n’est pas seulement des répétitions que les institutions préparatoires proposent à leurs élèves, ce sont aussi, et même surtout, des interrogations qui les préparent directement aux épreuves du concours . Le passage au tableau est le meilleur entraînement pour le préparationnaire . Malheureusement, dans les classes pléthoriques des spéciales parisiennes, il en a rarement l’occasion . C’est pourquoi les institutions multiplient les interrogations . Celles-ci sont collectives dans les conférences, où le préparateur cherche à éclaircir les difficultés du cours, et individuelles dans les examens, qui mettent les futurs candidats dans les conditions du concours . Dans les années 1840, chaque élève, chez Mayer (puis Debain) est interrogé tous les jours . Les examinateurs sont des professeurs de lycée, comme Menzas et Gérono, ou des répétiteurs de l’École polytechnique, comme Leverrier, Catalan, Delaunay et Wantzel . Chez Barbet, en 1844, pas moins de neuf professeurs jouent le rôle d’examinateurs permanents, venant deux fois par semaine, deux heures à chaque fois, pour interroger les élèves individuellement . Ceux-ci subissent, en outre, tous les trois mois un examen général . Chez Parchappe, à la même date, six personnes sont attachées comme examinateurs, “en sorte que chaque élève est souvent interrogé et exercé au tableau” . Toutes les institutions préparatoires adoptent ce système des “colles”, que l’on retrouve d’ailleurs à l’intérieur de l’École polytechnique où elles servent à la préparation des examens de passage et de sortie . Partout, il s’agit donc de “chauffer” les candidats en simulant les épreuves du concours qu’ils auront à affronter .»[2]

Nous voilà sur la bonne piste et, même si l’École polytechnique n’est plus la seule école visée par nos étudiants, ils continuent à se «chauffer» grâce aux «colles» pour les concours d’entrée aux grandes écoles .

Une différence notable, c’est que la «colle» n’est plus un examen individuel, les étudiants en prépa étant beaucoup plus nombreux qu’en 1840, ils sont rassemblés trois par trois dans ce qu’on appelle un «trinôme», et le colleur vient interroger chaque semaine un ou deux trinômes sur le programme en cours . Mais la colle se déroule toujours au tableau, au moins pour les interrogations de maths et de physique et l’examinateur est un professeur souvent «extérieur» c’est à dire qui ne connaît pas nécessairement les étudiants . Ceci donne à l’étudiant un sentiment des conditions réelles d’un concours, avec une interrogation par un inconnu qui, comme on va le voir, n’a pas toujours le même point de vue que son professeur habituel .

Dans un couloir hyperbolique

En plus des devoirs préparant à l’écrit des concours, les colles permettent essentiellement de préparer l’oral des concours et aussi de renforcer l’écrit par un suivi plus minutieux de la connaissance des cours .

En vue de cette préparation, chaque trinôme de colle rencontre les différents colleurs de manière périodique avec en moyenne deux ou trois heures de colles par semaine.

Les colles ont lieu dans toutes les matières : mathématiques, physique, chimie, sciences de l’ingénieur, français, langue vivante même si, à l’origine, elles portaient essentiellement sur les mathématiques . Au dire des élèves, les colles de mathématiques restent les plus redoutées au moins pour les filières d’ingénieurs ; il est vrai que faire des mathématiques à l’oral n’est pas naturel et c’est peut être la discipline qui semble la plus éloignée d’un exposé oral : nous sommes habitués à entendre des discours de physique, de biologie, de français, d’anglais, bien moins de chimie et encore moins de mathématiques . Nous reviendrons plus loin sur ce sujet .

L’emploi du temps de l’étudiant est donc assez bien garni et les heures laissées à la recherche personnelle sont assez restreintes . C’est souvent cette organisation un peu militaire due à la fréquence des devoirs et des colles qui fait que certains étudiants préfèrent la faculté au cadre strict des classes préparatoires, dites «prépas» : un étudiant m’a rapporté que le couloir où se déroulent les colles du lycée Saint-Louis est surnommé « le couloir de la mort » . C’est certes exagéré, mais les taupins aiment les hyperboles… même si celles-ci ont disparu des nouveaux programmes ! La richesse des enseignements va donc aussi de pair avec la lourdeur des horaires : chacun peut faire donc son choix et il n’est pas rare de voir des étudiants quitter la prépa à cause de son organisation trop intense pour partir à l’université .

My Taylor is not recursive

Chaque semaine, les professeurs dressent la liste des thèmes étudiés durant leur cours qui seront au programme des colles de la semaine suivante . Il y a donc des théorèmes, des démonstrations, des exemples classiques à connaître et réciter . Dans un premier temps, l’étudiant doit tout seul refaire le travail demandé . Dans un deuxième temps, en général le colleur donne un exercice à résoudre en direct au tableau sans préparation comme cela sera le cas le jour du concours . Les programmes de colles préparés par le professeur sont donc les références essentielles pour l’étudiant et le colleur . Certains professeurs suivent à la lettre le programme officiel, d’autres laissent plus libre cours à leur imagination et proposent des démonstrations qui ne sont pas forcément celles qui seront demandées le jour du concours mais qui présentent un intérêt pédagogique dans le cadre du cours . Par exemple dans une leçon sur l’analyse asymptotique, on peut demander de démontrer la célèbre formule de Taylor avec reste intégral : l’étudiant doit donc présenter la démonstration au tableau assez rapidement . En général, l’étudiant a au maximum quinze minutes pour répondre à la question de cours avant de passer à un exercice . Suivant sa dextérité, le colleur apprécie le niveau de l’élève et peut ajuster l’exercice qu’il proposera ensuite . Cette démonstration peut être apprise par cœur par l’élève sans forcément être bien comprise . S’il sent que c’est le cas, le colleur demandera alors quelques précisions et demandera aussi de l’écrire sur un exemple pour voir si l’élève est capable de la mettre en pratique, et éventuellement d’en tirer des conclusions sur une amorce de série entière comme dans le cas de la fonction exponentielle .

Certains étudiants n’aiment pas apprendre les démonstrations, ils estiment que cela ne sert à rien pour l’écrit et que c’est du temps perdu . Le professeur et le colleur doivent parfois se fâcher un peu pour que les plus récalcitrants se mettent au travail et apprennent le cours avant de venir en colle . Convaincre les étudiants de la nécessité d’apprendre, c’est tout le métier du professeur .

Mais la discussion n’est pas uniquement entre le professeur et les étudiants . Il n’est pas rare que les professeurs discutent entre eux sur la manière de démontrer tel ou tel théorème et, sans les colles, ce genre de conversation n’aurait sans doute jamais lieu .

Par exemple, la formule de Taylor avec reste intégral se démontre traditionnellement par récurrence . Rien de plus efficace pour manipuler les intégrales et les intégrations par parties . L’inconvénient bien sûr saute aux yeux : comment a-t-on pu avoir l’idée d’une telle formule ? La récurrence n’est-elle pas une simple vérification qui ne dit rien de la démarche initiale de découverte du mathématicien ?

Si je parle de cette formule, c’est que j’ai eu, il y a quelques années, une discussion avec un colleur sur la façon de la démontrer . En effet, il était surpris de voir à la place de la preuve classique par récurrence, celle de Lagrange qui a pratiquement disparu des manuels . Pourtant, cette démonstration, chère à l’historien des sciences Marco Panza [3], utilise les fonctions à deux variables et permet de trouver la formule finale par un principe télescopique simple même si l’étudiant n’a pas pu la retenir ou a oublié son expression . Elle a donc pour avantage de faire voir comment la formule prend forme . Me semblant plus riche et plus proche des méthodes de l’analyse que la démonstration par récurrence qui est surtout une démarche arithmétique, je l’ai toujours préférée et enseignée mais je ne pense pas que cela soit l’avis général des professeurs de mathématiques . Bref, une démonstration de mathématiques n’est pas neutre, et la colle, en rendant en quelque sorte publique les démonstrations des professeurs, est peut-être bien le lieu où l’originalité d’un professeur se révèle le plus à ses collègues et à ses étudiants .

Socrate dessinant

Un professeur d’histoire de mon lycée m’a un jour confié ne pas bien comprendre comment on pouvait faire des mathématiques à l’oral . Pour lui, une formule mathématique était vraie ou fausse et il ne voyait pas bien sur quoi pouvait porter l’argumentation de l’étudiant ou du colleur . Je n’ai pas trop su quoi lui répondre sur le champ, il est vrai que je ne suis pas aussi à l’aise que lui à l’oral, l’argumentation rapide n’étant pas en effet l’apanage du mathématicien !

Les mathématiques sont pour beaucoup de gens un langage écrit, ne serait-ce que par les signes algébriques difficiles à retenir si on ne les écrit pas. En effet, tout le monde garde le souvenir d’une équation du second degré à résoudre ou d’un système avec des \(x\) et des \(y\) sans trop se souvenir à quoi tout cela pouvait bien servir . Bien plus rares sont ceux qui gardent souvenir d’une question mathématique résolue à l’oral et non pas à l’écrit .

La colle de mathématiques en elle-même n’est pas un vrai oral . Ce n’est pas un écrit non plus … C’est un oral avec un tableau . L’étudiant écrit au tableau et le colleur le corrige ou discute avec lui . Le tableau est donc central dans la colle . Il est donc difficile de coller dans une classe ayant un petit tableau, il faut toujours un grand tableau surtout avec le trinôme de trois élèves . La première chose qu’apprend l’étudiant c’est de partager le tableau en trois car tout va dépendre de cette place dédiée qu’il faudra peut-être même défendre par rapport à ses coturnes prolixes risquant d’envahir son espace vital!

Dans le Ménon, Socrate demande à un jeune esclave de définir le côté d’un carré de surface double d’un carré donné . En termes modernes, il veut l’amener à découvrir tout seul la grandeur \(\sqrt{2}\) en tant que diagonale du carré unitaire . On a peut-être là le premier témoignage d’une colle dans l’Antiquité . Tout y est : on imagine Socrate traçant les carrés sur le sol et guidant son élève dans sa démarche . Il a sans doute à la main un outil, de quoi tracer ses figures et interroge grâce à elles le jeune esclave . De nos jours nous faisons un peu la même chose que Socrate .

Lors d’une colle je demandais à un élève de démontrer la formule \[\arctan\left(x\right)+\arctan\left(\frac{1}{x}\right)=\pm\frac{\pi}{2}\cdotp\]

C’était au programme de colle et, sûr de lui, il dérive puis intègre pour arriver au résultat . Je lui demande alors une démonstration géométrique qui, sans calcul, démontrerait que ces deux angles sont complémentaires . Devant son hésitation, je lui dessine alors au tableau un triangle rectangle avec des cotés adjacents à l’angle droit de longueurs \(1\) et \(x\).

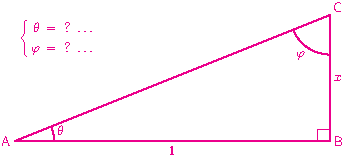
… mais la reconnaissance d’\(\arctan(x)\) en tant qu’angle dans le triangle n’a pas été immédiate . Il a fallu revenir plusieurs fois sur la figure pour que l’étudiant découvre enfin la formule qui y apparaissait .

Il est évident qu’une telle démarche ne pouvait pas se faire à l’écrit, ni même à l’oral, il fallait le tableau pour faire parler cette figure et la mettre en relation avec la formule abstraite .

La démarche de Socrate est bien sûr différente, le jeune esclave n’a aucune formule algébrique en tête contrairement à mon étudiant, puisque de toute façon l’algèbre n’existait pas au temps de Socrate, donc tout passe par la figure . De nos jours, c’est l’inverse qui se produit, tout passe par l’algèbre et la géométrie disparaît . Les formules seules restent ou laissent, comme dans le cas de mon professeur d’histoire, un souvenir bien vague qui fait croire que les mathématiques sont écrites essentiellement au lieu d’être dessinées et donc plus proches de l’oral : on peut raconter un dessin, un tableau car il y a une image spontanée, l’imagination se met en marche toute seule . L’imagination a beaucoup plus de mal à s’accrocher à une formule pour la faire parler .

La colle est de ce point de vue un remède à cette prédominance de l’algèbre au détriment de la géométrie, c’est à dire de l’abstrait par rapport au concret pour reprendre une formulation d’Auguste Comte [4] .

La difficulté des colles

Comme le rappelle le Littré dans sa définition, les questions posées en colle sont réputées «difficiles» . En effet, la préparation aux concours exige de confronter l’étudiant à des questions ardues parfois destinées à déstabiliser l’étudiant car les écoles d’ingénieurs veulent avant tout sélectionner les meilleurs . Ceci n’est pas à négliger mais il faut voir aussi que c’est la difficulté de l’exercice qui va rendre le dialogue possible . Une colle trop facile ne sert pas à grand-chose ; même si elle peut rassurer mentalement l’étudiant, elle ne va pas forcément le faire progresser .

La difficulté consiste généralement à donner à l’étudiant un énoncé inhabituel afin de briser certains automatismes et l’obliger à se remettre en question . Elle n’est ni gratuite, ni uniquement utile à un classement mais elle sert principalement à consolider les connaissances .

Par exemple dans le chapitre de probabilités et dénombrement, j’ai souvent posé l’exercice suivant :

Dans une course de chevaux, est-il plus facile de gagner un quinté dans le désordre ou un tiercé dans l’ordre?

L’étudiant met souvent un certain temps à cerner l’exercice et demande rapidement de l’aide. Alors je lui donne une piste : de quelle variable va dépendre le résultat ? S’il ne se rend pas compte qu’il faut faire intervenir le nombre de chevaux, je lui demande de considérer le cas où il n’y a que cinq chevaux. Ensuite, soit \(n\) le nombre de chevaux, peut-on former une équation pour \(n\)…?

La difficulté est donc la mise en équation puis la résolution pour faire intervenir arrangements ou combinaisons, et surtout le fait que l’étudiant doit lui-même faire intervenir ces notions-là . Si le cours est bien en tête l’exercice est en fait assez facile à résoudre . En revanche, le même exercice demandé à l’oral des concours est bien plus difficile car les notions de combinaison et d’arrangement sont vite oubliées si on ne les a pas revues récemment .

L’avantage des colles est donc de pouvoir doser les questions et d’amener le candidat lui-même à se poser les questions pour compléter un exercice et lui donner du sens .

Un autre intérêt des colles dans un exercice réputé difficile est la rapidité de la correction : pas besoin d’attendre le corrigé d’un devoir surveillé où, souvent une semaine après, l’étudiant a du mal à s’expliquer les erreurs qu’il a faites et à bien se souvenir de la démarche qu’il avait en tête . La colle permet de corriger beaucoup de confusions naissantes dans les très (voire trop) nombreuses notions abstraites qui sont à la disposition des étudiants .

La princesse Élisabeth, élève de Descartes, ne devait se concentrer que sur deux théorèmes pour résoudre les problèmes de géométrie [5,6]. Notre étudiant dispose de beaucoup plus de théorèmes (le cours de première année de classes préparatoires contient une centaine de théorèmes) et surtout des outils algébriques très riches qui sèment rapidement le trouble dans son esprit alors que justement la méthode cartésienne vise à la simplification .

Voici un exemple dans un cours d’algèbre linéaire qu’on pourrait croire assez facile, mais où les confusions dans les outils algébriques peuvent devenir inextricables . L’exercice était posé ainsi, suite au cours sur les déterminants d’ordre \(n\) :
Voici la recherche de l’étudiant que je retranscris telle qu’elle était au tableau :
\[\begin{aligned} \overrightarrow{\mathsf{AB}}\cdot\overrightarrow{\mathsf{AC}}= \overrightarrow{0}&\Longleftrightarrow \binom{b-a}{b’-a’}\cdot\binom{c-a}{c’-a’}=\binom{0}{0}\\ &\Longleftrightarrow\binom{b+c-2a}{b’+c’-2a’}=\binom{0}{0}\end{aligned}\]
Arrivé à ce point, l’étudiant se retourne vers moi en me disant qu’il ne sait pas comment arriver au résultat annoncé …

On devine aisément les égarements, les méprises accumulées dans la simple résolution de cet exercice : le produit scalaire au lieu d’un déterminant et le produit scalaire donnant un vecteur au lieu d’un réel . Même si l’étudiant est travailleur et volontaire, l’heure de colle est bien trop courte pour reprendre et rectifier les notions utilisées .

Il est vrai que la période de confinement a aussi perturbé beaucoup de nos élèves mais je pense que cela n’explique pas tout . Cet exemple montre combien l’étudiant raisonne en aveugle, au hasard, en mettant en place des connaissances encore trop hésitantes .

L’étudiant est dans un «tunnel» dont il cherche à sortir à tâtons . Il ne voit pas ce qu’il fait car il lui manque une image concrète des outils utilisés . Ici encore une image géométrique lui permettrait de voir que le produit scalaire est lié aux vecteurs orthogonaux et non aux vecteurs colinéaires . On peut confondre le déterminant avec un produit scalaire mais pas des droites orthogonales avec des droites parallèles !

La difficulté des colles peut donc venir d’une question dite «ouverte», où apparemment il n’y a pas de chemin classique pour le résoudre, ou d’une question simple et connue en apparence mais où les nombreuses notions utilisées ne sont pas encore maîtrisées et créent d’elles-mêmes des confusions dans l’esprit de l’étudiant .

Pour sortir enfin du tunnel

Il est certain que s’il n’y avait pas de colles, très peu d’étudiants feraient l’effort d’apprendre soigneusement les démonstrations, la pression des concours exigeant surtout pour eux de savoir faire des exercices .

Mais je pense que la nécessité des colles est bien plus philosophique que pratique dans l’intérêt des étudiants .

«Puisqu’une machine à compter est possible, une machine à raisonner est possible . Et l’algèbre est déjà une machine à raisonner ; vous tournez la manivelle, et vous obtenez sans fatigue un résultat auquel la pensée n’arriverait qu’avec des peines infinies . L’algèbre ressemble à un tunnel ; vous passez sous la montagne, sans vous occuper des villages et des chemins tournants ; vous êtes de l’autre côté, et vous n’avez rien vu .» [7]

Il me semble qu’Alain résume bien notre article : le problème est pour nos étudiants de voir des phénomènes propres aux mathématiques, de les mettre au grand jour, de ne pas faire des exercices en aveugle ou au hasard et de s’aider le plus possible de son imagination . Ce problème se pose moins en physique où les TP permettent à l’étudiant d’expérimenter à son tour, de confronter la théorie à la pratique et de se tromper librement sachant que le professeur pourra redresser rapidement l’expérience . Les mathématiques ont moins l’occasion de se confronter au réel et même cela ne fait guère partie de l’idée d’abstraction que l’on se fait ordinairement de cette discipline . Pourtant il faut toujours imaginer les objets pour les rendre habituels. Et imaginer sans pouvoir expérimenter directement . À ce titre la géométrie élémentaire est indispensable, par exemple pour le début de l’algèbre linéaire, pour l’étude des fonctions, la trigonométrie . Mais il faut très souvent forcer l’étudiant à faire les figures, car naturellement il est toujours pressé de connaître de nouvelles notions et ne se donne pas le temps de donner un sens à ses connaissances . La colle permet en partie de sortir de cette impasse, de voir concrètement les objets mathématiques en les dessinant au tableau par exemple . Cette démarche n’est malheureusement plus habituelle dans les cours trop surchargés de notions et où même les meilleurs perdent le contact avec le réel pour devenir des algébristes hors pair mais qui n’ont pas eu le temps de voir les paysages réels des mathématiques . Il est vrai que l’abstraction des mathématiques va de pair avec son utilité, sa généralisation à toutes sortes de domaines en dehors de la géométrie et de la mécanique, comme les probabilités ou l’informatique, et que le chemin est long avant d’y arriver, d’où la tentation de faire vite et de laisser de côté ce qui à l’origine était le cœur des mathématiques .

Il faut donc voir le plus possible et interroger les étudiants sur leurs représentations des mathématiques, et pourquoi pas refaire la démarche de Socrate dans le Ménon et demander à l’élève de tracer au tableau \(\sqrt{2}\) ou même \(\sqrt{a}\) comme le faisait Descartes ou, encore plus difficile, \(\sqrt[{\scriptstyle3}]{a}\) à l’aide de la cissoïde ?

Références

• [1] Littré. Monte-Carlo : Édition du Cap, 1968 .↩
• [2] Bruno Belhoste . « La préparation aux grandes écoles scientifiques au XIX^e siècle : établissement publics et institutions privées » . In : Histoire de l’éducation n°90 (2001) . , mis en ligne le 09 janvier 2009, consulté le 19 avril 2019 .↩
• [3] Giovanni Ferraro et Marco Panza . « Lagrange’s Theory of Analytical Functions ans His Ideal of Purity of Method  » . In : Archive for History of Exact Sciences. T. 66. N°2. 2012, pp95-197↩
• [4] Auguste Comte . Traité élémentaire de géométrie analytique à deux et à trois dimensions . Carilian-Goeury et Victor Dalmont, mars 1843, pp 21-22 ↩
• [5] Simone Weil. « Sur la science » . In : NRF / Collection Espoir . Gallimard, 1966. Chap. Science et perception dans Descartes (1929-1930), p. 25 .↩
• [6] René Decartes . Correspondance avec Elisabeth de Bohême et Christine de Suède . Lettre du 17 novembre 1643 . Galimard, 2013, p 52 .↩
• [7] Alain . Propos sur l’éducation . Édition Quadrige/Puf, novembre 2001, p. 164. ↩

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Ancien élève de classes préparatoires ayant intégré l’ENS Cachan puis devenu professeur de mathématiques en Physique Technologie de ces fameuses «prépas», au lycée Bourdelle à Montauban, Serge Radeff continue, à ses heures perdues, de lire des textes sur l’astronomie et la géométrie anciennes (Delambre et Tannery) ainsi que sur la philosophie des sciences .

---

1. Docteur en histoire (1982), Bruno Belhoste est professeur émérite d’histoire à l’Université Paris 1 Panthéon-Sorbonne et directeur de l’Institut d’histoire moderne et contemporaine de 2014 à 2017 .↩

---