À bas Euclide ?

Henrique Vilas-Boas commence son exploration du tableau L’École d’Athènes. L’occasion pour ses élèves de se frotter à Euclide et au raisonnement hypothético-déductif.

Je n’aurai pas le droit d’avoir des préférences pour un des deux côtés
Juste milieu je suis jusqu’à la fin des fins
C’est donc de ne pas savoir jamais, si je fais bien
Eugène Guillevic, Les Euclidiennes

Henrique Vilas Boas

© APMEP Mars 2022

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Euclide peut-il mourir deux fois ?

« À bas Euclide ! À bas le triangle ! » avait tonné en 1969, Jean Dieudonné, grand mathématicien, lors du séminaire proposé par l’OECE, future OCDE, faisant écho au programme « Mathématiques nouvelles » pour l’enseignement secondaire [1]. Cinquante-deux ans plus tard, les enseignements d’Euclide auraient-t-il disparu des programmes comme le souhaitait le mathématicien ? Certes non : aujourd’hui, s’il fallait choisir un mathématicien représenté dans l’École d’Athènes et central au collège, Euclide d’Alexandrie serait un excellent candidat.Précisément, la méthode hypothético-déductive et les nombreux résultats associés à son œuvre majeure en treize livres, les Éléments [2], ont impacté profondément la discipline et son enseignement durant plus de deux millénaires, au point d’en faire une clé possible pour appréhender la configuration disciplinaire des mathématiques [3]. Cet ouvrage a subi de très nombreuses critiques et commentaires, tant sur le contenu mathématique que pédagogique. Cela en fait par conséquent un marqueur culturel profond de la discipline. Paradoxalement, l’ouvrage s’est fossilisé dans les programmes scolaires pour devenir presque invisible [4]. Comme un lointain souvenir, Euclide a laissé son nom à une division donnant, chose rare au collège, deux résultats, un quotient et un reste, ainsi qu’à un algorithme pour déterminer le plus grand commun diviseur de deux nombres entiers. En effet, cette division et cet algorithme sont intimement liés dans la proposition 1 et 2 du livre VII. Sous sa formulation lapidaire, on peut supposer que Jean Dieudonné, excédé par une muséification des mathématiques, souhaitait avant tout abattre l’enseignement qui découlait des Éléments d’Euclide et non la personne. Et pour reprendre nos questions du précédent article [5], quelles mathématiques « euclidiennes » sont possibles et utiles ? Quelle place au concept de vérité ? À la contradiction ?

Les Éléments d’Euclide s’invitent dans ma classe

Dans le tableau de Raphaël, l’École d’Athènes, le personnage en bas à droite représente probablement Euclide qui trace une figure au compas, instrument hautement symbolique du géomètre de la Grèce antique. S’il s’agit bien d’Euclide, Raphaël sublime dans son tableau la Géométrie, fleuron des Éléments1. Que peut-on en faire au collège ? Voici quelques idées que je mène avec mes classes en lien avec cet ouvrage historique.

Dans ma classe

En Cinquième, j’introduis petit à petit quelques propositions des Éléments d’Euclide. Cela peut être l’occasion d’un travail sur l’aire d’un disque ou sur les angles alternes-internes. Pour ces derniers, un travail préalable est réalisé sur la symétrie centrale. Dans un premier temps, j’introduis les propositions2 n°s27 et 29 du livre I qui sont réciproques l’une de l’autre. La démonstration se fait oralement au tableau à l’aide de la symétrie centrale et par conservation des mesures des angles. Dans un second temps, je montre un texte de la démonstration de la proposition3 29. Il ne s’agit surtout pas de la lire en entier, j’attire plutôt l’attention sur le fait que la démonstration faite par Euclide ne convoque pas la symétrie centrale mais fait appel à d’autres idées. Nous décodons les éléments rédigés entre parenthèses (fig. 28, prop. 13, ax. 11) pour comprendre que la démonstration d’Euclide, d’une part est très différente de celle que j’ai proposée et, d’autre part qu’elle fait appel à d’autres propositions. Je peux introduire l’idée qu’Euclide utilise une chaîne logique pour aboutir à la démonstration d’un énoncé (par analogie avec ce que j’ai présenté où j’utilise une autre chaîne logique). Par ailleurs, la proposition 29 est aussi très utile pour construire un périscope [6] ou pour déterminer la circonférence de la Terre à la manière d’Erathostène [7], ces deux situations sont travaillées en classe avec les élèves.

Dans un troisième temps, j’introduis la proposition 32 [8] qui stipule que, dans tout triangle, la somme des mesures des trois angles d’un triangle vaut deux droits. Cette proposition est la conséquence de la proposition 29, c’est là de mon point de vue un joyau du livre I des Éléments. L’idée de « transporter » les angles pour former un angle plat est si lumineuse que tous les élèves peuvent y accéder.

Théorème 22 Proposition 32 du livre I des Éléments d’Euclide

En tout triangle, l’un des côtés étant prolongé, l’angle extérieur est égal aux deux côtés opposés intérieurs, et de chaque triangle les trois angles intérieurs sont égaux à deux droits.

Plusieurs exercices sont ensuite travaillés pour mobiliser ces trois propositions où les élèves s’initient à communiquer une démonstration.

Cette pratique est renouvelée en Quatrième et en Troisième. Ci-dessous quelques productions : l’une d’un élève de Cinquième (Reda) en mobilisant la proposition 32 du livre I et deux autres d’un élève de Quatrième (Muhammad) mobilisant la proposition 2 du livre VI (théorème de Thalès). Dans les copies d’élèves présentées ici, la référence donnée est celle de la numérotation des Éléments d’Euclide et non classiquement le nom du théorème (la proposition n° 32 n’en a pas). J’essaie de l’introduire pour tous les énoncés qui proviennent des Éléments ; néanmoins pour les plus classiques, les élèves ont le choix entre donner le nom classique et donner le numéro de la proposition en citant les Éléments d’Euclide. Certes il est plus facile de retenir le nom d’un théorème, c’est la pratique courante pour les mathématiciennes et mathématiciens professionnels, mais ces noms sont très rares dans la multitude des propositions travaillées à l’école et au collège. Par ailleurs, donner des noms à certaines propriétés peut laisser l’impression d’un aveuglement cognitif concernant ces propriétés au détriment d’autres propositions tout aussi importantes. Bien que je propose aux élèves d’écrire le théorème soit avec le nom, soit avec son numéro des Éléments, ce choix pose problème : que se passerait-il si un élève écrivait les références des Éléments sur sa copie au Brevet ? Il y a de quoi déstabiliser plus d’un collègue ! Gageons alors que le correcteur identifie dans ce type de trace une compétence culturelle mathématique de l’élève.

Un exemple en cinquième

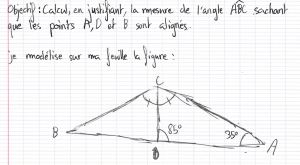
L’énoncé (source : cahier Sésamath Cinquième) et la production de Reda (ci-dessous). Pour déterminer l’angle \(\widehat{\mathsf{ABC}}\), il faut mobiliser deux fois la proposition n° 32 du livre I des Éléments d’Euclide (la somme des mesures des trois angles d’un triangle égale deux droits)
Premier exemple en quatrième

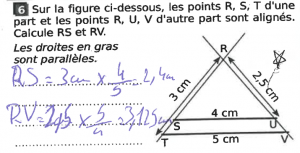
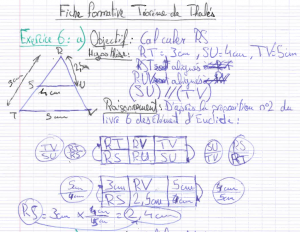
L’énoncé (source : cahier Sésamath Quatrième) et la production de Muhammad (ci-dessous). Pour déterminer la longueur \(\mathsf{RS}\), il faut mobiliser la proposition n° 2 du livre VI des Éléments d’Euclide (théorème de Thalès).
Second exemple en quatrième

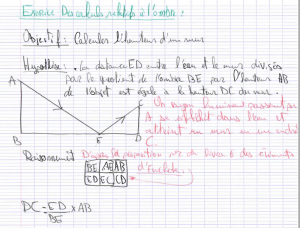
L’énoncé (source : Le calcul et la géométrie en Inde ancienne et médiévale de Catherine Morice-Singh) et une autre production de Muhammad (ci-dessous). Il faut aussi mobiliser la proposition n° 2 du livre VI moyennant un transport du triangle à l’intérieur du triangle \(\mathsf{BDE}\). L’approche est purement algébrique.

La démonstration « à la Euclide » contribue-t-elle à la formation du citoyen ?

S’il fallait argumenter en faveur de la démonstration « à la Euclide » au service d’une formation du citoyen, on peut émettre quelques propositions tout à fait favorables du point de vue cognitif, civique et moral. La démonstration « à la Euclide » s’inscrit dans une démarche dite hypothético-déductive [9], il faut noter d’emblée sa spécificité qui ne recouvre pas d’autres formes de raisonnements comme l’induction ou l’abduction4 par exemple, et qui participent sans nul doute, elles aussi, à la formation du citoyen. Il faut donc chercher du côté de cette démarche hypothético-déductive ce qui en fait son ferment et qui pourrait participer à la citoyenneté.

Du point de vue cognitif, l’exercice de la démonstration [10] hypothético-déductive est emblématique dans l’enseignement de la discipline, voire correspond à un certain moment de la philosophie : celui des ses commencements, marqué par des prises de conscience décisives [11]. L’exercice de la démonstration avec les élèves permet ainsi d’accéder aux normes mathématiques, ce que Jean-Yves Rochex définit par la normativité [12], dit autrement, la grammaire de la discipline.

Du point de vue civique et moral, développer l’exercice de la démonstration déductive impacte la qualité d’un débat, même alignée très imparfaitement à l’idéal d’un raisonnement [13] où toutes les implications sont explicitées.Les démonstrations à la manière d’Euclide, à la fois historiques et circonscrites à des formes particulières de la démonstration, permettent de donner à voir qu’en science on avance prudemment, qu’il faut se méfier des évidences, que chaque pas de raisonnement est important : c’est en cela un excellent modèle de rigueur pour les élèves, futurs citoyens qui seront amenés à prendre de la hauteur, à nuancer leur certitude. La certitude n’étant pas le vrai, cette exigence cruciale de la discipline est à rebours de la spontanéité et de l’impulsivité qui peuvent donner l’illusion du vrai. Cet horizon régulateur de la démonstration permet de donner à voir dans un débat citoyen par exemple, que soucieux du « poids » qu’exige une démonstration, le citoyen tempère ses convictions et écoute plus facilement celle de son contradicteur. Cette prudence pas à pas, a pour horizon une recherche d’objectivation, apprendre à penser pour soi-même, par soi-même et contre soi-même. En effet, après avoir émis une opinion, il ne s’agit pas nécessairement de la confirmer, mais de trouver les attributs propres aux objets discutés qui permettent d’articuler et (in)-valider différentes propositions. En somme, faire vivre de la contradiction5, penser contre l’opinion émise par soi ou par l’autre pour appréhender l’objet débattu, sans jamais se donner le dernier mot. Enfin, l’exercice de la démonstration reposant sur des objets a priori moins complexes que d’autres objets de la culture humaine, est de ce fait un excellent terrain pour se « faire la main » aux raisonnements déductifs.

Il m’est difficile de savoir à quel point mes élèves s’emparent de cette approche dans leur parcours d’apprenti citoyen, mais certaines de leurs traces écrites me donnent l’impression qu’ils prennent au sérieux cette prudence scientifique, au fur et à mesure qu’ils progressent dans l’année.

La difficulté de l’exercice de la démonstration suscite plusieurs alertes auxquelles il faut être vigilant : à qui s’adresse une démonstration ? Est-elle impersonnelle ? Suspendue dans le vide ? un discours sans agents ? ne risque-t-elle pas de s’imposer sans discussion possible sous l’effet de l’autorité de celui qui l’enseigne ? Peut-elle empêcher de penser si l’on confond de manière implicite le texte et l’idée de la démonstration ?

Les Éléments ? Demandez le programme !

En parcourant le programme de mathématiques en vigueur depuis 2015 au cycle 3 et 4, on trouve de nombreux objets présents dans les Éléments que j’ai essayé de répertorier dans le tableau ci-dessous. La liste n’est pas exhaustive.

Remarquons que la proposition « Si deux droites sont perpendiculaires à une même troisième alors elles sont parallèles », souvent étudiée en Sixième, est une variante du cinquième postulat.

Thème A — Nombres et calculs Définitions-Axiomes-propositions
Comprendre et utiliser les notions de divisibilité et de nombres premiers
Cycle 4 — Division euclidienne (quotient, reste).

  • (PGCD) Proposition 1 du livre VII
Cycle 4 — Multiples et diviseurs

  • Définitions 1, 2, 3, 4 et 5 livre VII
Cycle 4 — Nombres premiers

  • Définition 12 livre VII

  • (Infinité des nombres premiers) Proposition 20 livre IX

  • Décomposition d’un nombre entier en nombre premier, version plus « faible » Proposition 31 livre VII
Utiliser le calcul littéral
Cycle 4 — Utiliser le calcul littéral pour prouver un résultat général, pour valider ou réfuter une conjecture.

  • Distributivité Propositions 1, 2 et 3 livre II

  • Identité remarquable carré de la somme Proposition 4 livre II

  • Variante de la différence des carrés Proposition 5 livre II
Thème C — Grandeurs et mesures Définitions-Axiomes-propositions
Calculer avec des grandeurs mesurables ; exprimer les résultats dans les unités adaptées
Cycle 4 — Formule donnant le volume d’une pyramide, d’un cylindre, d’un cône ou d’une boule.

  • Aire d’un disque — version plus faible—Proposition 2 livre XII

  • Volume d’un prisme Proposition 31 livre XI

  • Volume d’une pyramide Proposition 7 livre XII

  • Volume d’un cône Proposition 12 livre XII

  • Volume d’une boule — version plus faible — Proposition 18 livre XII
Thème D — Espace et géométrie Définitions-Axiomes-propositions
Utiliser les notions de géométrie plane pour démontrer
Cycles 3 et 4 — Résoudre des problèmes de géométrie plane, prouver un résultat général, valider ou réfuter une conjecture.
Signification des sigles :
ACA = Angle-Côté-Angle
CAC = Côté-Angle-Côté
CCC = Côté-Côté-Côté

  • Caractérisation angulaire du parallélisme, angles alternes / internes Propositions 27 et 29 livre I

  • Médiatrice d’un segment Propositions 10 et 11 (problèmes) livre I

  • Somme des angles dans un triangle Proposition 32 livre I

  • Inégalité triangulaire Proposition 22 (problème) livre I

  • Cas d’égalité des triangles Proposition 4 livre I (CAC) Proposition 6 livre I (ACA) Proposition 8 livre I (CCC)

  • Triangles semblables-proportionnalité Propositions 4 et 5 livre VI

  • Parallélogramme : propriétés relatives aux côtés et aux diagonales Propositions 33 et 34 livre I

  • Théorème de Thalès et réciproque Proposition 2 livre VI

  • Théorème de Pythagore et réciproque Propositions 47 et 48 livre I
Thème E — Programmation et algorithmique Définitions-Axiomes-propositions

  • Algorithme PGCD Propositions 1 et 2 livre VII

Euclide s’efface derrière les Éléments

Après avoir exploré l’utilisation en classe des Éléments, intéressons-nous à la vie et l’œuvre du mathématicien. De la vie du mathématicien on ne sait quasiment rien, l’hypothèse la plus solide est qu’Euclide devait être un mathématicien actif dans certains domaines, soucieux d’organiser et d’exposer les connaissances scientifiques de son époque [15]. Force est de constater qu’Euclide s’efface littéralement derrière son ouvrage phare.Cette rigoureuse organisation mathématique, sans précédent, s’appuie sur des définitions, des axiomes, et cinq postulats. Les Éléments, terme finement choisi, sont les briques de l’ouvrage : des propositions démontrées selon les règles de la logique du tiers exclu introduit par Aristote, dont le dogme stipule qu’une proposition et son contraire ne peuvent être vrais simultanément.

On suppose qu’il a fallu accumuler et analyser de nombreux résultats pour déterminer ces briques, à l’instar de la chimie, et les articuler entre elles de manière déductive. On perçoit aussi qu’il a bien fallu interrompre ce processus et poser des principes non démontrés. C’est ce qui caractérise une approche atomiste de la pensée mathématique.

De ce long cheminement, il reste 465 propositions organisées selon trois grands domaines : géométrie plane, arithmétique et stéréométrie [16]. Le record étant obtenu par le très énigmatique livre X avec ses 115 propositions traitant de l’irrationalité de certains nombres. Si l’on considère les nombreux autres ouvrages d’Euclide, nous avons une véritable encyclopédie mathématique représentative des quatre branches que sont la géométrie, l’arithmétique, la musique et l’astronomie et qui connaîtra une postérité au Moyen-Âge, sous le nom de quadrivium, l’ensemble des arts mécaniques complémentaires des arts libéraux [17].

À partir des Temps modernes, le travail d’Euclide est remis en question, à la fois du point de vue logique et sur son choix de privilégier le côté déductif des raisonnements sans expliciter les idées et intuitions qui ont pu y mener. Ces controverses multiples sont détaillées dans la version numérique de cet article.

Un livre qui a fait ses preuves

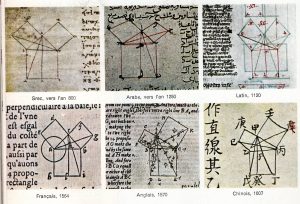
Cet ouvrage qui a fait le tour du monde (ci-dessus, la célèbre proposition 47 du livre I des Éléments dans différentes langues) doit son succès à la simplicité de ses principes, la rigueur de la démarche, l’apparente irréfutabilité des propositions. D’ailleurs, dès l’Antiquité, ce modèle donne l’envie à certains auteurs de rédiger des Éléments d’éthique, de physique, de théologie, etc.

Les savants arabes sous le règne du calife Al-Ma’mun au ixe siècle à Bagdad montrèrent un intérêt pour les Éléments d’Euclide, qui fut certainement parmi les premiers livres traduits du grec en arabe [18]. Quelques siècles plus tard, Baruch Spinoza, philosophe du xviie siècle, illustre parfaitement la poursuite du paradigme euclidien, comme le souligne Wim Klever : « Spinoza déduit les phénomènes humains, les affections et les comportements politiques, de principe et d’axiomes, qui sont établis exactement comme ceux d’Euclide. Son Éthique et sa Politique sont un élargissement et une continuation de la pratique d’Euclide. C’est pour ça qu’Euclide est son patron par excellence » [19]. Et même récemment, on trouve des défenseurs ardents des Éléments comme Nicolas Farès « Jusqu’à nos jours, des parties importantes des Éléments constituent des chapitres fondamentaux des programmes de la formation des enseignants […] à travers le monde » [20]. Il cite aussi l’édition de 1952 de l’Encyclopædia Britannica : « Le texte qui pourrait remplacer le livre d’Euclide n’a pas été écrit et, probablement, il ne le sera jamais ». En 1970, en réaction aux propos de Jean Dieudonné, Georges Métrios écrit un livre au titre sans équivoque : Vive Euclide ! (cf. [21]).

Un livre de vérités… très discutées !

On trouve tout d’abord des détracteurs de l’homme, c’est le cas d’Arnauld et Nicole (cf. [22]) au xviie siècle qui reprochent à Euclide « de plus rechercher la chaîne des démonstrations que la liaison des idées, de privilégier la certitude sur l’évidence et, par là, de négliger le vrai ordre de la nature ». C’est aussi le cas de certains historiens modernes qui pensent qu’Euclide serait dans l’hypothèse la plus extrême un simple compilateur de travaux tiers. L’œuvre n’est pas épargnée, une longue histoire critique commence avec Apollonius de Perge, proche contemporain d’Euclide. Il remet en cause dans le livre III des Éléments une construction qu’il estime incorrecte et incomplète, c’est la plus ancienne trace où il est fait mention des Éléments et c’est une critique (cf. [23]).

Au xvie siècle, Pierre de La Ramée (cf. [24]) initie une dispute mathématique et attaque avec virulence la logique du tiers exclu. Fondement de la démonstration euclidienne, elle sera remise en question par Jan Łukasiewicz [25] au début du xxe siècle avec les logiques trivalentes. Elles donneront naissance aux logiques modale, probabiliste et floue [26], elles-mêmes critiquées par le logicien contemporain Jean-Yves Girard [27]. D’autres voies alternatives seront poursuivies, à l’instar de Jan Brouwer, père de l’intuitionnisme, qui inscrit la dialectique comme moteur de la pensée mathématique (cf. [28]), et d’un choix troublant qui énonce que la négation d’une négation d’une proposition vraie n’est pas une proposition vraie [29]. Ce courant de pensée s’oppose radicalement à celui dit formaliste de David Hilbert [30] et sera le carburant d’une crise des fondements des mathématiques retentissante au début du xxe siècle [31].

Claude Tisseron, mon enseignant en maîtrise de mathématiques pures (sic), nous avait enseigné une critique de la proposition 1 du livre I qui donne une démonstration de la construction d’un triangle équilatéral. Euclide suppose implicitement que deux cercles se coupent forcément en un point, ce qui n’est pas nécessairement vrai si l’on construit des cercles sur le corps \(\mathbb{Q}\) des rationnels. Il serait très imprudent de faire ce procès au mathématicien, mais cet exemple souligne que les fondements du livre sont ancrés dans le sensible. La figure prévaut à notre insu dans cette démonstration.

Le doute s’est aussi immiscé très lentement sur les fondements même de l’ouvrage. De nombreux mathématiciens grecs, arabes et européens ont pensé qu’il était possible de démontrer le cinquième postulat à partir des quatre premiers. Au xviie siècle, dans cette perspective, Giovanni Saccheri souhaitait ainsi laver Euclide de toute souillure (cf. [32]). Au xixe siècle, on s’est rendu compte qu’il n’y avait rien à démontrer. Friedrich Gauss, Janos Bolyai, Nikolaï Lobatchevski ont levé le voile sur de nouveaux univers géométriques : les géométries dite non-euclidiennes. Est-ce une forme d’opposition ? On serait tenté d’y voir plutôt des ramifications d’une géométrie plus fondamentale, la géométrie absolue [33].

Jean Dhombres propose l’idée qu’il n’y a pas vraiment de rupture : « en cherchant à obtenir un texte unique et irréprochable les mathématiciens ont constamment réformé les textes plus anciens, ce qui peut paraître paradoxal car le texte recherché se voudrait définitif ». Finalement, d’après lui, « ces réformes aboutissent à des vrais changements de conception des mathématiques en phase avec l’histoire » [34].

Pour (ne pas) conclure

L’enseignement de la démonstration, en particulier l’approche hypothético-déductive, est un objet très complexe et elle est encore un enjeu majeur pour développer l’esprit scientifique de nos élèves. Les Éléments d’Euclide peuvent être un ouvrage de référence puissant pour ancrer une culture mathématique robuste et permettre aux élèves de percevoir qu’on peut en avoir un regard critique tout en respectant la pensée des Anciens. Il faut entendre les controverses qui montrent, à raison, le risque de muséification des résultats et de réduction de l’ouvrage à un formulaire bureaucratique. Faire accéder les élèves au patrimoine cognitif et culturel d’une démonstration, sa diversité conceptuelle et langagière est donc au cœur de l’activité des enseignants.

L’exploration du tableau de Raphaël continue, nous nous retrouverons pour un prochain numéro avec le génial Archimède, dont la bibliographie est très prolifique. Son approche par exhaustion peut-être initiée dès le cycle 3, nous proposerons une approche qui mobilise en partie ces concepts.

Références

  • [1] Claude Lelièvre. Blog. Exemple n° 5.↩

  • [2] Στοιχεία, Éléments. Œuvres numérisées par Marc Szwajcer Exemple n° 5.↩

  • [3] Dominique Lahanier-Reuter. Conscience disciplinaire, configuration disciplinaire et vécu disciplinaire. Exemple n° 5.↩

  • [4] Julien Netter. Le curriculum invisible. Exemple n° 5. 2020.↩

  • [5] Henrique Vilas-Boas. « L’École d’Athènes s’invite au collège ». In : Au fil des maths n° 541 (juillet-septembre 2021). Exemple n° 5.↩

  • [6] Henrique Vilas-Boas. Chaîne youtube. Un périscope de fortune (Sésamath, ex. 1 p. 242) Exemple n° 5.↩

  • [7] Maude Chambert et Adlen Ayache. Monsieur Eratosthène, comment mesurer la circonférence de la Terre ? Élèves de Cinquième, blog TERRE (journal scientifique du collège Paul-Emile Victor) Exemple n° 5.↩

  • [8] Henrique Vilas-Boas. Chaîne youtube. Prop. 32 Livre 1 Exemple n° 5.↩

  • [9] Robert Blanché. L’axiomatique. PUF.↩

  • [10] Étienne Ghys, Aurélien Alvarez et Joys Leys. Dimensions. Exemple n° 5.↩

  • [11] Nathalie Chouchan. Les mathématiques. Flammarion. ↩

  • [12] Jean-Yves Rochex. Avec Henri Wallon et Lev Vygotski. Exemple n° 5.↩

  • [13] Claire Ravez. Regards sur la citoyenneté à l’école. Dossier de veille de l’IFÉ Exemple n° 5. Lyon, juin 2018.↩

  • [14] Heinz Wiesmann et Adèle Van Reeth. Les chemins de la philosophie, le mystère Héraclite. Épisode 3/4 : l’impossible rencontre avec le réel. Exemple n° 5.↩

  • [15] Bernard Vitrac. Euclide le Stoichéiôtês. Exemple n° 5. ↩

  • [16] Les Éléments d’Euclide. Exemple n° 5.↩

  • [17] Fabio Acerbi. Euclide. Exemple n° 5.↩

  • [18] François Jacquesson. Géométrie égalitaire. Exemple n° 5.↩

  • [19] Wim Klever. « Le concept de la mathématique de Spinoza ». In : Séminaire de philosophie et mathématiques n° 1 (1990). Exemple n° 5, pp. 1-12.↩

  • [20] Nicolas Farès. Euclide et l’algèbre. Exemple n° 5. 2018.↩

  • [21] Michel Criton et Bertrand Hauchecorne. La querelle des maths modernes. Exemple n° 5.↩

  • [22] Henry Plane. « À bas Euclide ! » In : PLOT nouvelle série n° 6 (juin 2004). Exemple n° 5, pp. 18-19. ISSN : 0397-7471.↩

  • [23] Bernard Vitrac. « Euclide le fondateur ». In : Les génies de la science Les géomètres de la Grèce antique. N° 21 (novembre 2004). Exemple n° 5.↩

  • [24] Édouard Mehl. « Euclide et la fin de la Renaissance : sur le scholie de la proposition 18 du livre XIII ». In : tome 56. N° 2 (2003). Exemple n° 5. ISSN : 0151-4105. DOI : 10.3406/rhs.2003.2195.↩

  • [25] Jan Łukasiewicz. Exemple n° 5. Wikipedia.↩

  • [26] Didier Dubois et Henri Prade. « Traiter le flou et l’incertain ». In : Dossier Pour la science Les chemins de la logique. N° 49 (1er octobre 2005). Exemple n° 5.↩

  • [27] Jean-Yves Girard. « La logique comme géométrie du cognitif ». In : Logique, dynamique et cognition (2007). Sous la dir. de Jean-Baptiste Joinet. Exemple n° 5, pp. 13-29.↩

  • [28] Olivier Keller. « Une occasion manquée, l’intuition de la dialectique dans l’intuitionnisme de Brouwer ». In : Quadrature n° 119 (janvier-mars 2021).↩

  • [29] Jean-Yves Girard. Des règles de la logique à la logique des règles. Conférence Exemple n° 5.↩

  • [30] Jean-Yves Girard. Les fondements des mathématiques. Canal-U Exemple n° 5.↩

  • [31] M. Combes. Fondement des mathématiques. PUF, 12 juillet 1985. ISBN : 978-2130314585.↩

  • [32] B. Ycart. Histoire de mathématiques. Exemple n° 5 et Exemple n° 5.↩

  • [33] Éric Charpentier. Géométries euclidiennes et non-euclidiennes. Exemple n° 5. 22 novembre 2018.↩

  • [34] Jean Dhombres. D’Euclide à Bourbaki, la réforme permanente. Exemple n° 5. 12 février 2015.↩

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅


Henrique Vilas Boas est enseignant de mathématiques en REP+ depuis 20 ans, chargé d’études au centre Alain Savary à l’Institut français d’éducation et ancien formateur académique éducation prioritaire au centre académique Michel Delay.

  1. De nombreux doutes existent quant aux véritables auteurs des Éléments, on pense par exemple que le livre X a été écrit par Théétète.↩︎

  2. Proposition 27 livre I : si les angles alternes sont de même mesure alors les droites sont parallèles.↩︎

  3. Texte issu de l’ouvrage Éléments d’Euclide, éditions du Kangourou.↩︎

  4. En logique, l’abduction est l’action d’inférer les prémisses les plus vraisemblables permettant de parvenir, par déduction, à une conclusion concordante aux observations Wiktionaryarticle abduction. ↩︎

  5. Au sens « le dire s’oppose au dit » [14].↩︎

Pour citer cet article : Vilas Boas H., « À bas Euclide ? », in APMEP Au fil des maths. N° 543. 24 juin 2022, https://afdm.apmep.fr/rubriques/eleves/a-bas-euclide/.