Triangulation et impression 3D
(complément)
Imprimer en 3D cache en réalité pas mal de mathématiques : essentiellement de la géométrie dans l’espace ; mais en arrière-plan, on voit poindre quelques résultats de la topologie des surfaces. L’utilisateur ne voit pas les mathématiques car ce sont les logiciels qui les prennent en charge. Dans cet article qui complète celui de la revue papier, Aurélien Alvarez se propose de nous les dévoiler en nous présentant tous les calculs nécessaires pour imprimer un tétraèdre.
Aurélien Alvarez
© APMEP Juin 2019
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Dans l’article Triangulation et impression 3D, nous expliquons le principe de l’impression 3D et le lien avec la triangulation des surfaces.
Nous proposons dans cet article d’écrire un programme permettant de générer un fichier STL contenant les données d’impression d’un tétraèdre régulier.
Ces deux articles complémentaires peuvent être lus indépendamment l’un de l’autre, ce dernier ayant pour but de permettre aux plus enthousiastes de lancer concrètement des impressions 3D des polyèdres réguliers.

Nous commençons par rappeler le principe général de l’impression 3D et ce qu’est le format STL.
Très souvent, on utilise un logiciel de modélisation à partir duquel on exporte un fichier STL du modèle que l’on souhaite imprimer.
Pour autant, peut-on écrire le fichier STL du modèle que l’on souhaite imprimer sans passer par un logiciel de modélisation ?
La complexité d’un modèle peut rapidement rendre la tâche particulièrement fastidieuse mais, sur des exemples simples comme les polyèdres, en particulier le tétraèdre qui ne comporte que quatre faces triangulaires, il s’agit d’un exercice très instructif, nous semble-t-il.
Nous avons choisi d’écrire nos programmes en swift ![]() mais aucune réelle spécificité de ce langage n’est utilisée, de sorte que chacun est libre de réécrire les lignes de code que nous allons présenter dans son langage de programmation préféré.
mais aucune réelle spécificité de ce langage n’est utilisée, de sorte que chacun est libre de réécrire les lignes de code que nous allons présenter dans son langage de programmation préféré.
Impression 3D et format STL
Le principe général de l’impression 3D
Le principe général du fonctionnement d’une imprimante 3D est de fabriquer des volumes solides par ajout progressif de matière.
Avant de pouvoir lancer l’impression d’un objet, il faut d’abord disposer d’un modèle numérique 3D de celui-ci.
Le fichier du modèle 3D est ensuite analysé par le logiciel d’impression de l’imprimante qui est en charge d’organiser le découpage en tranches des différentes couches de matière qui seront déposées les unes sur les autres afin de fabriquer l’objet.
Le logiciel d’impression de l’imprimante convertit donc le modèle 3D en instructions précises que la machine est capable de comprendre et d’exécuter.
L’imprimante dépose finalement la matière couche après couche, lentement mais sûrement, jusqu’à obtenir le volume souhaité.






À leurs débuts, les imprimantes 3D utilisaient bien souvent des résines, alors que depuis les années 2010, d’autres matériaux sont plébiscités, en particulier certains plastiques comme le PLA ou l’ABS.
C’est d’ailleurs le cas de l’imprimante da Vinci 1.0 Pro 3in1 ![]() que nous avons utilisée ici.
que nous avons utilisée ici.
-
Le PLA est biodégradable, issu de matériaux recyclés, et il est assez courant de l’utiliser dans l’industrie alimentaire (comme emballage !). Il ramollit autour de 50°C, commence à fondre à 160°C et peut être réellement travaillé à partir de 180°C. En plus d’être sensible à l’humidité, le PLA a tendance à casser facilement si on le contraint trop fortement.
-
L’ABS quant à lui est un polymère thermoplastique que l’on retrouve dans les appareils électroménagers ou dans les jouets Lego. Il ramollit autour de 90°C, commence à fondre à 180°C et peut être réellement travaillé vers 230°C. Il est donc plus résistant à la chaleur que le PLA et se plie facilement sans rompre.
Le PLA et l’ABS ont chacun leurs avantages et leurs inconvénients mais il est en général plus facile de réaliser des impressions avec le PLA qu’avec l’ABS car ce dernier résiste mal aux chocs de température.
Bien choisir entre le PLA ou l’ABS selon l’objet que l’on souhaite imprimer est davantage une question d’expérience que de science…
Le format STL
De nombreux logiciels de modélisation sont disponibles, y compris des logiciels gratuits et multiplateformes.
Ces logiciels permettent de modéliser des formes géométriques complexes à l’aide d’outils de base très simple, comme par exemple l’outil d’extrusion.
Une fois le logiciel pris en main et avec un peu d’habitude, on peut modéliser un tétraèdre et un cube en quelques clics, comme illustré sur l’image suivante extraite du logiciel SketchUp ![]() .
.
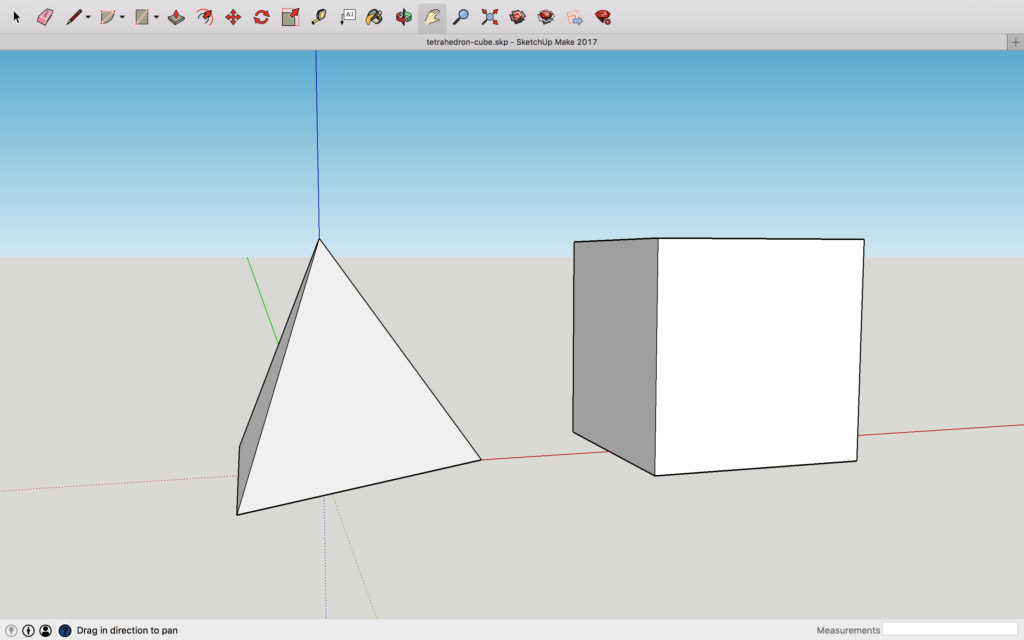
Pour imprimer le tétraèdre ci-dessus, il nous suffit alors de demander à notre logiciel de modélisation d’exporter le modèle 3D vers un fichier au format STL qui sera traité par le logiciel d’impression de l’imprimante.
Le temps d’impression dépend essentiellement de la taille de l’objet à imprimer et du taux de remplissage de celui-ci : cela peut donc aller de quelques minutes à de longues heures.
Pendant ce temps, avec un simple éditeur texte, rien n’interdit de jeter un œil au fichier STL en question.
On découvre alors quelque chose comme ceci.
|
Le format STL est très répandu de nos jours, son nom provient du mot stéréolithographie (STL pour STereo-Lithography).
D’après Wikipédia :
La stéréolithographie est une technique, dite de prototypage rapide, qui permet de fabriquer des objets solides à partir d’un modèle numérique.
L’objet est obtenu par superposition de tranches fines de matière.
Le développement industriel de cette technique date des années 1980 et fut initié aux États-Unis par Charles W. Hull.
Notons que le format de fichier STL ne décrit que la géométrie de surface d’un solide alors qu’un modèle numérique de conception assistée par ordinateur contient bien souvent des informations complémentaires comme la couleur, la texture, etc.
Regardons de plus près ce fichier.
La première ligne contient le mot réservé solid suivi du nom que l’on a choisi pour l’objet au moment de l’exportation (ici tetrahedron) et la dernière ligne contient ce même nom après le mot réservé endsolid.
Le reste du fichier est composé de blocs commençant par le mot réservé facet et terminant par le mot réservé endfacet.
|
À l’intérieur d’un bloc, les coordonnées de trois sommets sont indiquées, ainsi que les coordonnées de la normale au triangle formé par ces trois sommets et pointant vers l’extérieur du volume.
Les coordonnées de la normale sont précédées par le mot réservé normal et celles de chacun des sommets par le mot réservé vertex.
Dans notre exemple, on lit quatre blocs facet–endfacet correspondant chacun à l’une des quatre faces du tétraèdre.
On vérifie également que les quatre normales indiquées dans le fichier sont bien des vecteurs de norme \(1\).
En résumé, un fichier STL contient essentiellement les données de triangulation de la surface de l’objet que l’on souhaite imprimer.
En effet, tous les objets que l’on imprime, même s’ils peuvent sembler lisses quand on les prend en main, sont en fait décrits par une multitude (parfois des dizaines de milliers) de petits triangles plats.
Écrire un programme qui génère un fichier STL
L’espace affine euclidien
Nous allons utiliser le type Float pour représenter les nombres réels ; un vecteur de \(\mathbb{R}^3\) est alors la donnée d’un triplet de Float.
La structure standard d’espace vectoriel est encodée par l’opération d’addition \(+\) sur les vecteurs et par la multiplication externe \(\).
|
Nous munissons à présent l’espace vectoriel \(\mathbb{R}^3\) de sa structure euclidienne usuelle (la norme d’un vecteur est la racine carrée de la somme des carrés de ses coordonnées) et définissons une fonction qui normalise un vecteur.
|
Enfin nous introduisons la structure affine de \(\mathbb{R}^3\) : un point de \(\mathbb{R}^3\) est repéré par ses trois coordonnées et il est possible d’opérer sur tout point une translation par un vecteur quelconque ou une homothétie centrée en l’origine \(\mathsf{O}\).
|
Une autre manière de préciser la structure affine est d’indiquer la fonction \(\texttt{affineStruct} : \texttt{Vertex} \times \texttt{Vertex}
\longrightarrow \texttt{Vect}\) qui, étant donné deux points \(\mathsf{A}\) et \(\mathsf{B}\) de \(\mathbb{R}^3\), calcule l’unique vecteur \(\overrightarrow{v_{\mathsf{AB}}}\) tel que \(\mathsf{B} = \mathsf{A} +
\overrightarrow{v_{\mathsf{AB}}}\), ce qui est une façon équivalente de dire que l’espace vectoriel \(\mathbb{R}^3\) opère librement et transitivement dans l’ensemble \(\mathbb{R}^3\).
|
Des sommets, des arêtes, des faces et des polyèdres
Après avoir défini la notion de point, ou plutôt de sommet (Vertex), nous définissons à présent la notion d’arête qui est spécifiée par un sommet origine et un sommet terminal ; la méthode opp() permet de calculer l’opposée d’une arête et la méthode toVect() transforme une arête en un vecteur.
|
La fonction suivante calcule le produit vectoriel de deux vecteurs de \(\mathbb{R}^3\).
|
Nous définissons maintenant la notion de face par la donnée de trois sommets ordonnés ; la méthode normal() calcule le vecteur normal unitaire à la face et la méthode opp() calcule la face opposée1.
Sans difficulté, on vérifie d’ailleurs que le vecteur normal unitaire de la face opposée est l’opposé du vecteur normal unitaire de la face de départ.
Autrement dit, pour tout f de type Face, on a
f.opp().normal() \(=\) – f.normal().
|
Nous terminons cette série de définitions avec la notion de polyèdre : ce sera pour nous n’importe quelle structure qui contient une liste de sommets, une liste d’arêtes et une liste de faces.
Du point de vue mathématique, il conviendrait d’être plus précis ici en spécifiant que les sommets de la liste d’arêtes appartiennent à la liste des sommets, et de même pour les arêtes des faces.
Mais ce ne sera pas nécessaire pour notre besoin car nous appliquerons nos définitions dans des cas très précis comme celui du tétraèdre régulier dont nous connaissons bien la combinatoire.
|
De la triangulation au STL
Pour mémoire, rappelons qu’il s’agit de générer un fichier dont le motif général est le suivant.
|
La fonction suivante \(\texttt{STLwrite : [Face]} \times \texttt{Float}
\longrightarrow \texttt{Void}\) prend en entrée une liste de faces, un facteur d’échelle et, pour chaque face de la liste, imprime à l’écran le motif général rappelé ci-dessus avec les coordonnées des normales unitaires aux faces, ainsi que les coordonnées des sommets des faces.
|
Le tétraèdre régulier en STL
Voici à présent la définition de la structure polyédrale de tétraèdre : quatre sommets P, Q, R, S, six arêtes orientées PQ, PR, PS, QR, RS, SQ, et quatre faces orientées PQR, PRS, PSQ, QSR.
|
Interlude mathématique
Nous détaillons à présent la construction du tétraèdre régulier et faisons quelques calculs afin de déterminer des coordonnées explicites pour ses sommets.
On désigne par \(\mathbb{R}^4\) l’espace affine euclidien de dimension \(4\) muni du produit scalaire usuel et rapporté au repère canonique \((\mathsf{O},
(\overrightarrow{e_1}, \overrightarrow{e_2}, \overrightarrow{e_3},
\overrightarrow{e_4}))\).
Le tétraèdre régulier est par définition l’enveloppe convexe des quatre points \(\mathsf{P} = \mathsf{O} + \overrightarrow{e_1}\), \(\mathsf{Q} =
\mathsf{O} + \overrightarrow{e_2}\), \(\mathsf{R} = \mathsf{O} +
\overrightarrow{e_3}\) et \(\mathsf{S} = \mathsf{O} + \overrightarrow{e_4}\).
L’isobarycentre de ces quatre points, c’est-à-dire le centre du tétraèdre régulier, est le point \(\mathsf{O}’ = \dfrac{1}{4}(\mathsf{P} + \mathsf{Q} +
\mathsf{R} + \mathsf{S})\).
En coordonnées, on a donc \(\mathsf{P} = (1, 0, 0, 0)\), \(\mathsf{Q} = (0,
1, 0, 0)\), \(\mathsf{R} = (0, 0, 1, 0)\), \(\mathsf{S} = (0, 0, 0, 1)\) et \(\mathsf{O}’ = \dfrac{1}{4} (1, 1, 1, 1)\).

Les quatre points \(\mathsf{P}\), \(\mathsf{Q}\), \(\mathsf{R}\), \(\mathsf{S}\), et donc le tétraèdre régulier en entier, appartiennent à l’hyperplan affine euclidien \(\mathcal{H}\) d’équation \(x_1 + x_2 + x_3 +
x_4 = 1\).
Un vecteur normal unitaire à cet hyperplan est le vecteur \(\overrightarrow{n} = \dfrac{1}{2} (1, 1, 1, 1)\).
On vérifie facilement que \((\mathsf{O}’ , (\overrightarrow{u_1},
\overrightarrow{u_2}, \overrightarrow{u_3}))\) est un repère orthonormal de l’hyperplan \(\mathcal{H}\), où \(\overrightarrow{u_1}\), \(\overrightarrow{u_2}\) et \(\overrightarrow{u_3}\) sont, dans la base orthonormée \((\overrightarrow{e_1}, \overrightarrow{e_2}, \overrightarrow{e_3},
\overrightarrow{e_4})\), les vecteurs de coordonnées \(\overrightarrow{u_1} =
\dfrac{1}{\sqrt{2}} (1, -1, 0, 0)\), \(\overrightarrow{u_2} = \dfrac{1}{2} (1,
1, -1, -1)\) et \(\overrightarrow{u_3} = \dfrac{1}{\sqrt{2}} (0, 0, 1, -1)\).
Le calcul du déterminant des quatre vecteurs \((\overrightarrow{u_1}\), \(\overrightarrow{u_2}\), \(\overrightarrow{u_3}\), \(\overrightarrow{n})\) donne \(1\), ce qui fait de cette base une base directe.
Des calculs élémentaires permettent désormais d’exprimer les coordonnées des points \(\mathsf{P}, \mathsf{Q}, \mathsf{R}, \mathsf{S}\) dans le repère orthonormal \((\mathsf{O}’ , (\overrightarrow{u_1}, \overrightarrow{u_2},
\overrightarrow{u_3}))\) de \(\mathcal{H}\).
On trouve \(\mathsf{P} = \dfrac{1}{2}(\sqrt{2}, 1, 0)\), \(\mathsf{Q} =
\dfrac{1}{2}(-\sqrt{2}, 1, 0)\), \(\mathsf{R} = \dfrac{1}{2}(0, -1,
\sqrt{2})\) et \(\mathsf{S} = \dfrac{1}{2}(0, -1, -\sqrt{2})\).
Le centre de la face \(\mathsf{PQR}\) est l’isobarycentre de ses trois sommets, c’est-à-dire le point \(\mathsf{C} = \dfrac{1}{3}(\mathsf{P} +
\mathsf{Q} + \mathsf{R})\) de coordonnées \(\dfrac{1}{6}(0, 1, \sqrt{2})\).
On en déduit qu’un vecteur normal à cette face dirigé vers l’extérieur du tétraèdre est le vecteur \(\overrightarrow{\mathsf{SC}} = \dfrac{2}{3}(0, 1,
\sqrt{2})\).
Le calcul du produit vectoriel \(\overrightarrow{\mathsf{PQ}} \wedge
\overrightarrow{\mathsf{PR}}\) donne le vecteur \(\dfrac{3}{2}\overrightarrow{\mathsf{SC}}\), ce qui assure que la face \(\mathsf{PQR}\) est bien orientée.
On en déduit finalement la liste des quatre faces orientées, à savoir les faces \(\mathsf{PQR}\), \(\mathsf{PRS}\), \(\mathsf{PSQ}\) et \(\mathsf{QSR}\).
Le fichier STL du tétraèdre régulier
Nous reprenons les calculs des coordonnées des sommets du tétraèdre régulier que nous avons faits précédemment, ce qui nous permet de définir quatre points P, Q, R et S qui seront les sommets de notre tétraèdre.
En choisissant un facteur d’échelle de \(100\), nous nous préparons à imprimer un tétraèdre de côté \(100 \times \sqrt{2}\) mm, soit environ 14 cm.
|
Si nous importons le code STL généré ci-dessus dans le logiciel d’impression de notre imprimante, nous constatons que le tétraèdre ne se présente pas dans une position propice à l’impression2…
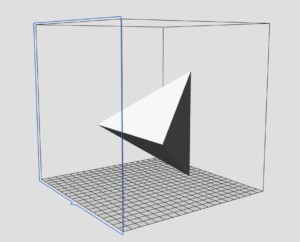
En regardant attentivement les coordonnées des sommets du tétraèdre, on comprend que le sommet qui touche le plateau de l’imprimante est S (puisque sa coordonnée en \(z\) est la plus petite des quatre), et ce sont les points P et Q qui sont sur la même horizontale (puisqu’ils ont leurs coordonnées en \(z\) égales, en l’occurrence nulle).
On identifie sur la figure l’axe \((\mathsf{O}x)\) et l’axe \((\mathsf{O}y)\) en notant que les coordonnées en \(y\) de P et Q sont égales (leurs coordonnées en \(x\) étant opposées).
On en déduit qu’il faudrait appliquer une rotation de notre modèle d’un certain angle \(\theta\) suivant l’axe \((\mathsf{O}x)\).
Un calcul élémentaire de trigonométrie permet de voir qu’il s’agit en fait d’une rotation d’angle \(\theta\) tel que \(\tan(\theta)= -\dfrac{\sqrt{2}}{2}\), ou encore \(\cos(\theta) = \sqrt{\,\dfrac{2}{3}\,}\) et \(\sin(\theta) = -\sqrt{\,\dfrac{1}{3}\,}\cdotp\)
Plutôt que de demander à notre logiciel d’impression d’appliquer cette rotation, il est presque aussi simple de reprendre notre programme et d’étendre la structure Vect avec une méthode qui opère comme une rotation d’angle theta suivant l’axe des \(x\).
|
De là, nous définissons une fonction de rotation globale du tétraèdre : plus précisément, il s’agit d’une rotation d’angle theta dont l’axe de rotation est dirigée suivant l’axe \((\mathsf{O}x)\) et passe par \(\mathsf{S}\).
|
…puis nous retentons notre chance !
|
Cette fois, le fichier STL généré correspond à un tétraèdre qui se présente parfaitement bien pour l’impression puisque l’une de ses faces, à savoir la face PSQ, est horizontale : il ne reste plus cette fois-ci qu’à lancer l’impression !
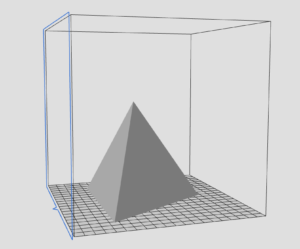
Nous laissons en exercice le cas du cube, objet un peu plus complexe puisque constitué de six faces carrées que l’on peut chacune trianguler avec deux triangles en choisissant une diagonale dans chaque face, ou bien par quatre triangles en rajoutant un sommet au centre de chaque face.
Fichiers sources
Tous les codes sources discutés dans cet article sont disponibles dans ce dépôt GitHub ![]() :
:
Remerciements
Ce travail d’impression 3D a été réalisé au FabLab du laboratoire d’informatique (LIFO) de l’université d’Orléans.
Merci aux collègues qui fréquentent régulièrement ce lieu pour leur enthousiasme et leurs conseils avisés.
Référence
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Aurélien Alvarez est enseignant-chercheur à l’Institut Denis Poisson, le laboratoire de mathématiques des universités d’Orléans et de Tours, et formateur au centre national de la Fondation La main à la pâte. Il participe à de nombreux projets de diffusion de mathématiques et est le rédacteur en chef de la revue en ligne Image des mathématiques
.
-
Puisque l’on convient d’appeler face la donnée de trois sommets ordonnés, la face opposée est la donnée de ces trois mêmes sommets ordonnés dans l’autre sens. Concrètement, si \(\mathsf{ABC}\) est une face, \(\mathsf{CBA}\) est la face opposée.↩
-
Bien que cela paraisse évident, c’est une erreur que l’on commet souvent au début : on ne peut pas déposer de la matière dans le vide ! Ainsi, si l’on souhaite imprimer une table toute simple, constituée d’un plateau et de quatre pieds, il faut l’imprimer à l’envers, de sorte que la machine commencera d’abord par le plateau et finira par les quatre pieds.↩

Une réflexion sur « Triangulation et impression 3D web »
Les commentaires sont fermés.