Mathématiques du jonglage
Vincent Pantaloni nous propose une promenade dans les mathématiques du jonglage : parabole, permutation, tresse, moyenne, … sont au programme !
Vincent Pantaloni
© APMEP Septembre 2019
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Modélisation
Les univers du cirque et des mathématiques semblent être parallèles. Et pourtant, l’art millénaire du jonglage recèle des mathématiques variées découvertes récemment. Initiée par Claude E. Shannon (celui de la théorie de l’information), cette utilisation des mathématiques dans le jonglage a même permis de créer de nouvelles figures.
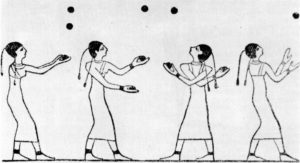
Figure 1 : Fresque égyptienne, environ 2000 av. J.-C.
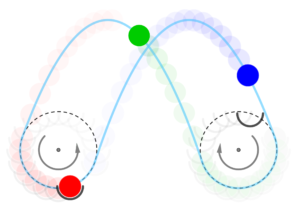
Commençons par essayer de représenter le jonglage classique avec trois balles. Les mains du jongleur, dont le mouvement est figuré en pointillés, tournent en sens contraire. Les lancers ont lieu à l’intérieur et les balles sont rattrapées à l’extérieur.
 |
 |
|
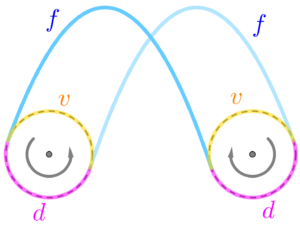
La figure de droite illustre les trois temps \(v\), \(d\) et \(f\) considérés par Shannon dans son théorème. Une main est alternativement vide (pendant un temps \(v\)) puis pleine quand elle contient une balle (qui y demeurera un temps \(d\)). Une balle vole pendant un temps \(f\) puis atterrit dans une main, où elle restera pendant un temps \(d\). |
Si on regarde la même scène du dessus, les balles vont de droite à gauche puis de gauche à droite. Il sera pratique de représenter ces positions variant dans le temps par un schéma où le temps s’écoule vers le bas comme ceci :

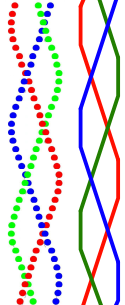
Ci-dessous, on a déroulé le mouvement sur une période, et on observe un motif de tresse à trois brins. On peut d’ailleurs effectivement obtenir une vraie tresse si on jongle avec des cordes accrochées aux balles comme figuré sur cette photo. Jongler, c’est tresser, et il y a une théorie mathématique des tresses qui s’applique à ces diagrammes que l’on utilise en jonglage. Avec cette modélisation nous allons pouvoir démontrer le théorème de Shannon.
 |
 |
Théorème de Shannon
On sait peu que Claude E. Shannon, père de la théorie de l’information, était aussi un jongleur à qui l’on doit la première mathématisation du jonglage et l’invention des premiers automates jongleurs alors qu’il était au MIT. Il a formulé le premier théorème du jonglage dans son article Scientific aspects of juggling ![]() . Si on essaye de passer du jonglage à trois balles au jonglage à quatre puis cinq balles (et plus si affinités) on se rend vite compte qu’il va falloir lancer les balles plus haut.
. Si on essaye de passer du jonglage à trois balles au jonglage à quatre puis cinq balles (et plus si affinités) on se rend vite compte qu’il va falloir lancer les balles plus haut.
On utilisera le théorème de Shannon pour déterminer à quelle hauteur il faut lancer les balles pour un jonglage régulier avec un nombre donné de balles. On appelle jonglage régulier un jonglage où chaque main fait le même lancer à chaque fois à un rythme constant.
| Théorème 1 (SHANNON) |
|
Pour un jonglage régulier avec \(B\) balles, on a : \[\frac{f+d}{v+d}=\frac{B}{H}\] où les lettres \(f\), \(d\), \(v\) et \(H\) désignent :
|
Cela peut prêter à sourire de considérer le nombre de mains comme un paramètre, mais on peut jongler à une main et même trois, quatre ou plus si on a des amis jongleurs. Nous allons donner une démonstration de ce théorème dans le cas \(H=2\) (deux mains) et \(B=3\) (trois balles). Le principe se généralise bien.
Démonstration : on utilise la représentation en tresse, avec le temps s’écoulant vers le bas.
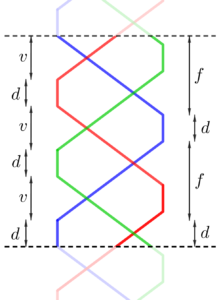
Une période est figurée entre les pointillés et on peut y lire les différents temps utilisés par Shannon. Si on regarde la balle bleue (avec les temps notés à droite) : elle est lancée de la main gauche, vole pendant un temps \(f\), puis elle atterrit dans la main droite où elle reste un temps \(d\) avant de voler vers la main gauche où elle restera encore un temps \(d\). Ainsi une période dure \(f+d+f+d=2(f+d)\). On compte par ailleurs une période en observant la main gauche qui est soit vide, soit pleine, recevant chacune des trois balles. Une période dure donc aussi \(3(v+d)\), ainsi : \[2(f+d)=3(v+d).\] En divisant de part et d’autre par \(2(v+d)\), on obtient : \[\frac{f+d}{v+d}=\frac{3}{2}\cdotp\] Ce qui est bien le résultat annoncé pour le cas \(H=2\) et \(B=3\).
▀
En partant du théorème de Shannon on peut exprimer le temps de vol \(f\) en fonction des autres variables en multipliant par \((v+d)\) :
\[\tag{10}
f = (v+d)\frac{B}{H} -d.\]
Cette dernière relation montre que \(f\) est une fonction affine croissante du nombre de balles \(B\). Ainsi, plus on veut jongler avec un nombre important de balles, plus il faut augmenter leur temps de vol \(f\). Comment augmenter \(f\) ? En lançant les balles plus haut, bien sûr ! Déterminons la hauteur des lancers pour un jonglage régulier à \(B\) balles.
Hauteur des lancers pour jongler avec balles.
Étant uniquement soumise à l’accélération de la pesanteur \(g\) (environ \(10\,m·s^{-2}\) sur Terre), la loi de la chute des corps nous dit que chaque balle met un temps \(t\) pour tomber d’une hauteur \(h\), liés par la relation :
\[\tag{10}
h=\frac{1}{2}\,gt^2.\]
Comme une balle met autant de temps pour monter à la hauteur \(h\) que pour en retomber, on a \(f=2t\) et donc \(h=\dfrac{1}{2}\,g \left(\dfrac{f}{2}\right)^2\cdotp\) Soit pour \(g=10\), après simplification : \(h=\dfrac{5}{4}\,f^2\). En combinant ce résultat avec l’équation obtenue grâce au théorème de Shannon, on a donc : \[h = \frac{5}{4}\left((v+d)\frac{B}{H}-d\right)^2.\] Pour un jonglage à deux mains (\(H=2\)), et en prenant pour \(v\) et \(d\) un temps d’un quart de seconde \(\left(v=d=\dfrac{1}{4}\right)\), on obtient :
\[h = \frac{5}{4}\left(\frac{B}{4} -\frac{1}{4}\right)^2\]
ce qui se réarrange (en arrondissant le rationnel au centième) en \(h\approx{0,08}(B-1)^2\).
| Propriété 1 |
|
Pour un jonglage régulier à \(B\) balles il faut lancer chaque balle à une hauteur \(h\) (exprimée en mètres) environ égale à \({0,08}(B-1)^2\). |
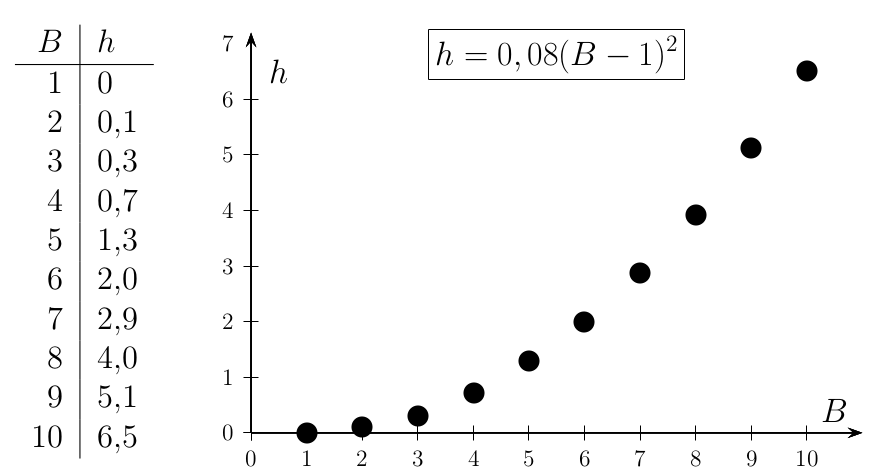
Figure 2 : Hauteur des lancers en mètres en fonction du nombre de balles.
La hauteur évolue comme le carré du nombre de balles, une balle de plus augmente considérablement la difficulté. Pour éviter d’avoir à lancer trop haut, on peut diminuer \(v+d\), c’est à dire effectuer des rotations plus rapides des mains. Les hauteurs pour huit, neuf, dix balles peuvent sembler exagérées, mais vous pouvez regarder sur des vidéos de Bruce Sarafian ![]() avec différents records pour huit, neuf, dix, onze et douze balles ou d’Alex Baron
avec différents records pour huit, neuf, dix, onze et douze balles ou d’Alex Baron ![]() avec treize balles pour observer la rapidité des mains et les hauteurs impressionnantes des lancers.
avec treize balles pour observer la rapidité des mains et les hauteurs impressionnantes des lancers.
Siteswap
Si vous cherchez des tutoriels pour apprendre à jongler, vous rencontrerez peut-être un étrange code appelé siteswap utilisé par les jongleurs pour décrire des figures de jonglage. Par exemple pour apprendre à jongler avec cinq balles on recommande de commencer par maîtriser le jonglage normal à quatre balles puis s’entraîner au \(55550\) et au \(552\). De jolies figures à trois balles sont codées par \(441\) ou encore \(5241\). Que signifient ces nombres1 ?
Il est recommandé pour visualiser les figures de jonglage dont on donnera le code siteswap d’utiliser l’application gratuite pour smartphone et tablette.
Origines de la notation
La notation siteswap inventée par Paul KLIMEK en Californie a été développée indépendamment et simultanément en 1985 par deux groupes : d’une part Bruce TIEMANN et Benêt MAGNUSSON (étudiants au California Institute of Technology et d’autre part en Angleterre à Cambridge par Mike DAY et les jeunes mathématiciens Colin WRIGHT et Adam CHALCRAFT. Le jonglage était en vogue et il y avait besoin d’un système pour décrire une figure de jonglage (qui, en pratique, nécessitait des figures de positions des balles à divers instants et de longues descriptions).
Principe de la notation
On reprend le schéma de la tresse, où on représente le temps qui s’écoule vers le bas. On effectue le premier lancer de la main à gauche au point rouge. Les numéros ①, ②, ③, … sur le schéma ci-dessous représentent l’ordre des mains qui vont lancer alternativement à un rythme régulier.
|
L’intervalle de temps entre deux mouvements de main est pris comme unité de temps. On ne tient pas compte dans cette modélisation des temps \(v\) et \(d\) utilisés dans le théorème 1. À partir de là on peut coder les différents lancers par le nombre de temps qu’il faudra à la balle pour retomber. |
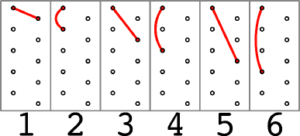
-
La balle est lancée rapidement (\(1\) temps) dans la main opposée, elle fuse quasiment à l’horizontale.
-
La balle est lancée et rattrapée par la même main, pas très haut (10 cm). En pratique, on ne la lance pas : elle reste dans la main pendant un temps qui équivaut à deux lancers \(1\) (un aller-retour rapide).
-
La balle est lancée dans la main opposée mais plus haut (environ d’après les données vues sur la figure 2) puisqu’il lui faut trois temps pour retomber. Dans le même temps on doit pouvoir faire trois lancers \(1\). C’est le lancer pour jongler la classique cascade à trois balles que nous avons illustrée au début.
-
La balle est lancée verticalement (à environ 70 cm) pour retomber dans la même main.
-
Lancer croisé haut, environ 1,3 m. Pour la cascade à cinq balles.
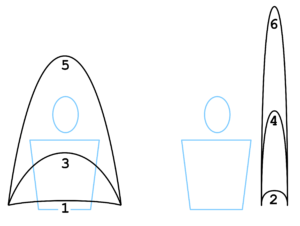
Figure 3. Lancers impairs (croisés) et pairs (non croisés).
Et ainsi de suite, les lancers impairs sont croisés et les lancers pairs sont verticaux et retombent dans la même main. On peut alors désigner une figure de jonglage par la succession de ces nombres entiers : c’est son siteswap. On donne juste le code sur un cycle puisqu’en général une figure de jonglage est périodique. Par exemple \(5241\) correspond à lancer un \(5\), puis un \(2\), puis un \(4\), puis un \(1\) et à recommencer. On écrit \(5241\) mais il faut comprendre \(524152415241\dots\) jusqu’à ce qu’une balle tombe. On peut tout aussi bien désigner ce jonglage par le siteswap \(1524\) ou toute autre permutation circulaire.
Nous conservons ici le mot anglais siteswap (littéralement l’échange de site) qui est utilisé en France et dont l’origine sera expliquée plus loin.
Exemples de siteswaps
On a cité des exemples de siteswaps : \(441\) ou \(5241\) qui se font avec trois balles. On peut aussi citer \(501\) (un jonglage à deux balles) ou \(55550\) (avec quatre balles) qui comportent un zéro. Un zéro signifie qu’il n’y a pas de balle dans la main à ce moment et donc… on ne lance pas de balle. Vous êtes invités à ouvrir l’application et à entrer ces siteswaps dans le menu Pattern Entry pour voir un automate programmé qui jongle cette figure.
| Essayez aussi \(12345\) dont voici le diagramme en échelle. Pour tracer ce diagramme, on part du haut et on note les nombres \(12345\)–\(12345\)… alternativement sur chaque point. Ensuite on trace les lancers correspondants en partant de chaque point. On observe que le \(5\) est indépendant, il est toujours fait avec la même balle bleue. Les deux autres motifs identiques sont faits par deux balles (rouges) qui subissent finalement les lancers \(1\), \(2\), \(4\), \(3\). | 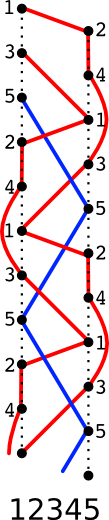 |
Le siteswap \(12340\) correspondrait au même jonglage en supprimant la balle bleue.
Les jonglages réguliers correspondent aux siteswaps de période 1. La cascade à trois balles est simplement codé par \(3\). Plus généralement le jonglage régulier à \(n\) balles se code par \(n\). La figure 4 montre les tresses régulières pour les jonglages réguliers à trois, quatre et cinq balles. On observe que le jonglage régulier à quatre balles ne croise pas : tout se passe comme si on jonglait avec deux balles dans chaque main.
Figure 4 : Tresses pour les jonglages réguliers à trois, quatre, cinq balles.
Questions mathématiques sur le siteswap
Si vous vous amusez à rentrer des siteswaps au hasard dans Juggling Lab, comme \(1234\) ou même \(12\) vous verrez le message « Invalid pattern ». Si \(12345\) fonctionnait bien, \(1234\) ou \(12\) ne semblent pas jonglables, pourquoi ?
Le siteswap \(12\) ne peut pas être jonglé comme le montre le diagramme en échelle ci-dessous car deux balles arriveraient simultanément dans la même main. Plus généralement, dès que l’on a une succession de deux entiers consécutifs dans l’ordre décroissant comme \(21\), \(32\), \(43\), …, les deux balles arriveront ensemble dans la même main, ce qui pose problème.
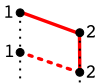
De même \(1234\) n’est pas jonglable car si on le lit \(2341\) on voit les lancers \(3\) et \(1\) distants de deux dans le siteswap qui arriveront en même temps puisque \(3-1=2\). C’est en fait la seule condition pour qu’un siteswap soit jonglable : on ne doit pas avoir deux nombres entiers \(a\) et \(b\) dans cet ordre, distants de \(d\) dans le siteswap tels que \(a-b=d\). Cette condition équivaut à dire que deux balles ne tombent pas simultanément dans la même main.
En pratique cette condition n’est pas évidente à vérifier de tête et on verra une condition nécessaire plus simple en corollaire au théorème de la moyenne qui nous donne le nombre de balles nécessaires pour jongler un siteswap jonglable. Nous allons maintenant présenter une transformation sur les siteswaps qui à la fois explique ce nom et nous permettra de démontrer le théorème de la moyenne avant d’ensuite l’utiliser pour inventer de nouveaux tours de jonglage.
Une transformation sur les siteswaps
Il est temps d’expliquer l’origine du mot siteswap. Dans le diagramme en échelle on a le point (site) de départ et d’arrivée de chaque balle. Si on considère deux balles lancées successivement, on peut en gardant les mêmes points de départ intervertir leur point d’arrivée sans perturber le reste de la séquence. On a échangé (to swap en anglais) les sites d’arrivée. Qu’est-ce que cela change à la paire de nombres considérée ?
Regardons d’abord un exemple : \(51\).
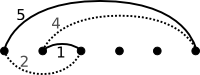
Par rapport au temps zéro, on prévoit l’arrivée de la première balle dans cinq temps et de la deuxième dans deux temps (puisqu’elle sera lancée un temps après la première). Si on fait l’échange des arrivées (en pointillés), la première balle lancée arrivera dans deux temps (on lance donc un \(2\)) et la deuxième arrivera dans cinq temps il faudra donc lancer un \(5-1=4\).
Ainsi on a par cet échange des sites d’arrivée : \(51\longmapsto 24\). On peut remarquer que si on refait l’échange des arrivées à partir de \(24\) on retombe sur \(51\). On vient de voir sur cet exemple une transformation sur deux nombres consécutifs d’un siteswap.
| Définition 1 |
|
On définit l’application \(\mathrm{E}\) (comme Échange) de \(\mathrm{N}*\times\mathrm{N}\) dans \(\mathrm{N}*\times\mathrm{N}\) par : \[\tag{$\mathrm{E}$} |
| Propriété 2 |
|
Pour tous \((a,b)\) dans \(\mathrm{N}*\times\mathrm{N}\) qui sont deux lancers consécutifs d’un siteswap jonglable, les remplacer par \(\mathrm{E}(a,b)\) donne encore un siteswap jonglable. |
On remarque que la somme reste constante après cette transformation : \(b+1+a-1=a+b\). Cette technique permet de créer de nouvelles figures de jonglage à partir de tours existants. Cela ne change pas le nombre de balles. Par exemple, on a déjà vu \(12345\) avec trois balles. En bouclant, un \(5\) est suivi d’un \(1\). \(1234{51}2345\). On peut lui appliquer la transformation \(\mathrm{E}\) : \(51\longmapsto 24\) pour obtenir \(1234{24}2345\).
On remarquera que, même si le nombre de balles n’a pas changé et que le reste du motif est demeuré identique, on a dû recolorier les balles après la transformation \(\mathrm{E}\) dans le diagramme en échelle.
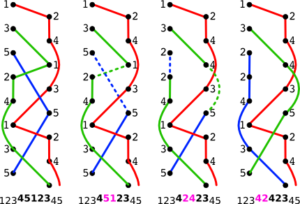
Mais pourquoi s’arrêter là ? On remarquera que :
| Propriété 3 |
|
Si une suite périodique d’entiers n’est pas constante, on peut trouver deux termes consécutifs \(a\) et \(b\) avec \(a > ; b\). |
Démonstration : notons \((a_n)_{n\in\N}\) une suite périodique non constante d’entiers. Notons \(p\) le plus petit entier non nul tel que \(a_p\) est égal au maximum de la suite. La suite étant périodique et non constante, on peut considérer le plus petit rang \(q\) après \(p\) tel que \(a_q\neq a_p\). Par définition de \(p\) et \(q\) on a alors : \(a_p=a_{q-1}> ;a_q\).
▀
Théorème de la moyenne
Ainsi, tant qu’il y a des nombres différents dans un siteswap, on peut toujours en trouver deux qui se suivent comme \((a,b)\) avec \(a > ; b\). On opère alors l’échange des arrivées \((a,b)\longmapsto(b+1,a-1)\). L’écart entre les nombres a diminué de deux. Cette transformation \(\mathrm{E}\) conserve la somme, donc la moyenne des deux nombres tout en les rapprochant de leur moyenne. Poursuivons notre exemple, voici la succession des transformations en partant de \(12345=45123\) : \[4{51}23\longmapsto {42}423\longmapsto 33{42}3 \longmapsto 33333\]
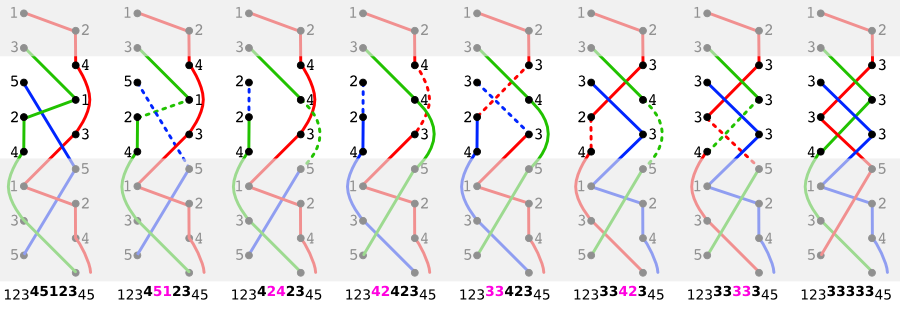
Comme chaque application de la transformation \(\mathrm{E}\) conserve le nombre de balles et un siteswap valable, on en déduit que \(12345\) se jongle avec autant de balles que \(33333\), c’est à dire avec \(3\) balles. À chaque étape le total \(T\) reste inchangé : \(T=1+2+3+4+5=3+3+3+3+3\) soit \(T=5\times3\). Le nombre constant \(3\) qu’on trouve in fine correspond donc à \(\dfrac{T}{\mathstrut5}\) soit le total divisé par la longueur du siteswap. Ainsi le nombre de balles nécessaire pour jongler le siteswap \(12345\) correspond à la moyenne des nombres du siteswap. Ce résultat est général.
Ce qui a été fait sur cet exemple peut toujours se faire avec cet algorithme de retour à la moyenne :
-
Prendre un siteswap \(S\) jonglable non nul ;
-
Tant que \(S\) comporte des nombres différents faire :
-
Opérer une permutation circulaire pour mettre le maximum de \(S\) en premier,
-
Prendre les deux premiers nombres \((a,b)\) consécutifs tels que \(a> ;b\) et les transformer en \(\mathrm{E}(a,b)\) :
\[(a,b)\longleftarrow (b+1,a-1)\]
-
-
Fin du Tant que ;
-
Renvoyer le siteswap \(S\).
L’affectation \((a,b)\longleftarrow (b+1,a-1)\) produit toujours une paire différente ; en effet, on a vu que pour un siteswap jonglable, on a toujours \(a\neq b+1\). Ainsi, en un nombre fini d’étapes cet algorithme permet d’obtenir un siteswap de même longueur, avec un même total et qui ne comporte que des nombres identiques.
On en déduit le théorème de la moyenne :
| Théorème 2 (de la moyenne) |
|
de la moyennemoyenneTout siteswap jonglable est tel que la moyenne de ses nombres est égale au nombre de balles nécessaires pour le jongler. |
Exemples
-
\(441\) se jongle avec trois balles car \[(4+4+1)\div{3}=3\ ;\]
-
\(5241\) se jongle avec trois balles car \[(5+2+4+1)\div{4}=3\ ;\]
-
\(552\) se jongle avec quatre balles car \(12\div3=4\) ;
-
\(421\) ne se jongle pas2 puisque \(4+2+1=7\) et \(7\) n’est pas divisible par \(3\).
Ce théorème donne donc une condition nécessaire pour qu’un siteswap soit jonglable.
| Corollaire |
|
Pour qu’un siteswap soit jonglable il est nécessaire que la moyenne de ses nombres soit un nombre entier. |
Par exemple \(1234\) de moyenne \({2,5}\) n’est pas jonglable. Plus généralement, \(123\ldots n\) ne peut être jonglable que si \(n\) est impair puisque sa moyenne est : \[\frac{1}{n}\times \frac{n(n+1)}{2}=\frac{n+1}{2}\cdotp\]
Une condition nécessaire mais non suffisante
La condition énoncée par le corollaire ci-dessus n’est pas suffisante pour garantir qu’un siteswap soit jonglable. Comme on le voit sur le diagramme en échelle, on peut jongler \(123\). Comme \(\dfrac{6}{\mathstrut3}=2\) c’est un jonglage à deux balles (!). Cependant \(321\) n’est pas jonglable car au troisième temps on aurait trois balles arrivant dans la même main. Donc la propriété de la moyenne ne suffit pas ; cet exemple montre aussi que pour un siteswap jonglable donné, une permutation des nombres n’est pas toujours jonglable.
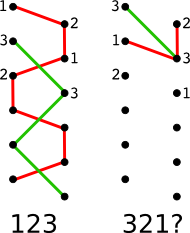
Cependant, on a le théorème de réarrangement qui est une conséquence d’un théorème de Marshall Hall qu’on trouve dans l’article A combinatorial problem on abelian groups ![]() paru dans Proceedings of the American Mathematical Society en 1952 :
paru dans Proceedings of the American Mathematical Society en 1952 :
| Théorème 3 (de réarrangement) |
|
Tout \(n-\)uplet d’entiers naturels de moyenne entière peut être réordonné de manière à obtenir un siteswap valide. |
La preuve mathématique de ce théorème est loin d’être évidente, on en trouvera une adaptation par Dean Hickerson pour le jonglage sur le groupe de discussion ![]() .
.
Créer de nouvelles figures par transformation
Nous avons utilisé la transformation d’échange des points d’arrivée pour « moyenner » un siteswap et le rendre régulier. Il est intéressant de noter que l’on peut faire le contraire pour créer à partir d’un jonglage régulier un tour plus complexe. Par exemple, dans le jonglage régulier à quatre balles, les balles ne changent pas de main (on ne croise pas). Certains spectateurs, lorsqu’ils s’en rendent compte, disent que « c’est de la triche », voire que c’est trop facile (avant d’avoir essayé). Deux techniques étaient connues des troubadours pour croiser les lancers en jonglant à quatre balles mais le jonglage n’est plus régulier. Alors, comment passer du jonglage régulier \(4\) à un jonglage avec des lancers impairs ?
On peut appliquer la transformation \(\mathrm{E}\) d’échange des points d’arrivée pour deux lancers consécutifs : \(44\longmapsto 53\). Si on le fait une fois, on croise deux balles (la bleue et la verte sur le diagramme ci-dessous). Mais on peut aussi remplacer tous les \(44\) par des \(53\) et alors on ne fait que croiser, c’est ce qui est représenté sur la troisième tresse. Le motif n’est plus symétrique, on remarque par exemple que c’est toujours la même main qui lance les \(3\) et l’autre qui lance les \(5\). On a une figure appelée demi-douche, où des lancers hauts (\(5\)) passent au dessus des lancers bas (\(3\)), on ne voit pas la figure en forme de symbole \(\infty\) comme pour la cascade à trois balles.

Figure 5 : Du jonglage régulier 4 (non croisé) au siteswap 53 croisé.
L’autre technique connue pour effectuer des lancers croisés avec quatre balles comportait deux lancers croisés hauts (deux \(5\)). On peut trouver ce jonglage avec un échange de sites espacé de deux temps. En effet, on peut généraliser la transformation d’échange en ne prenant pas des lancers nécessairement consécutifs mais espacés d’un temps \(t\).
| Propriété 4 (échange généralisé) |
|
D’un siteswap valide de la forme \(a{\dots}b\) où \(a\) et \(b\) ont des positions séparées de \(t\) on peut obtenir un autre siteswap valide en le transformant en \((b+t){\dots}(a-t)\). |
Exemples
-
\(444\longmapsto 642\) pour \(t=2\) ;
-
\(4444\longmapsto 7441\) pour \(t=3\).
Si on applique cette transformation pour \(t=2\) à \(445344\) obtenu précédemment, on obtient, en échangeant un \(4\) et un \(3\) : \(4{4}5{3}44
\longmapsto 4{5}5{2}44\). Ainsi \(444\) peut être remplacé par \(552\) qui est donc un siteswap jonglable.
Figure 6 : Du jonglage régulier 4 (non croisé) au siteswap 552 croisé.
Ce jonglage paraît saccadé car on lance deux fois de suite avec la même main (gauche, gauche, droite, droite, gauche, gauche, …).
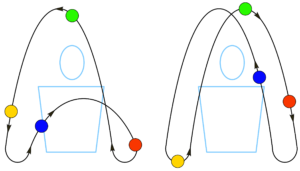
Figure 7. Siteswap 53 (à gauche) comparé à 552 (à droite).
À la fin des années 1980 à l’université de Cambridge, Colin et ses collègues inventaient la notation siteswap. Colin m’a raconté que c’est en observant ces suites de nombres qui correspondaient à des jonglages connus mais qu’ils venaient de coder en \(53\) et \(552\) qu’ils se sont dit qu’il y avait peut-être possibilité de poursuivre la suite logique en tentant \(5551\).
En effet, si on part de \(5353\), en échangeant deux \(3\) (pour \(t=2\)) on obtient \(5551\) : \(5{3}5{3}\longmapsto 5{5}5{1}\).
Le siteswap \(5551\) est donc une figure jonglable (bien que difficile), et elle n’avait jamais été jonglée avant. Colin raconte volontiers que lors de festivals de jonglage, les amateurs voulaient voir et apprendre ce nouveau tour découvert qui venait d’être récemment inventé. On peut également aller jusqu’à \(55550\) qui correspond au jonglage régulier à cinq balles mais où il manque une balle (il faudrait un \(5\) en place du \(0\)).
|
La clarté d’une notation mathématique adaptée a révélé l’existence de jonglages jusqu’alors inconnus. |
Conclusion
On a vu que le jonglage comportait depuis peu une théorie mathématique alors que c’est une activité pratiquée depuis la plus haute Antiquité comme on le voit sur l’illustration égyptienne d’ouverture. La hauteur des lancers est déterminée par le théorème de et la loi de la chute des corps. La notation siteswap est maintenant adoptée par beaucoup de jongleurs à travers le monde car c’est une notation simple et utile en pratique. On peut demander à un jongleur d’un autre pays s’il sait jongler \(441\), il comprendra bien la question. Si on ne sait pas ce qu’est \(441\), ou \(5241\), l’information est suffisante pour essayer de le jongler : on calcule d’abord la moyenne pour voir qu’il faut trois balles puis les nombres indiquent les lancers à effectuer successivement. En général, on n’y arrive pas du premier coup pour autant… Il est satisfaisant de savoir que cette notation efficace a permis de découvrir des tours de jonglage jusqu’alors inconnus et finalement, avec la notion d’état, de déterminer tous les jonglages possibles. On dispose des graphes3 qui permettent de créer aisément n’importe quelle figure périodique… ou non. Cela peut même se programmer, par exemple l’application peut renvoyer tous les siteswaps jonglables avec comme données : le nombre de balles, la hauteur maximale et la longueur de la période. On peut même considérer les marches aléatoires sur ces graphes afin de créer un jonglage aléatoire. À vos balles !
Références
-
Florent Hivert. Jonglerie, automates et combinatoire.
-
Allen Knutson. Conférence de Cornell University (Mathematics of Juggling)..
-
Mathématiques et jonglerie. Éduscol..
-
Bulkard Poster. The Mathematics of Juggling. Springer.
-
Colin Wright. Co-inventeur du siteswap.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Vincent Pantaloni est IA-IPR de mathématiques. Il a eu l’occasion d’enseigner la théorie mathématique du jonglage en classe de Seconde lors de cours de DNL, ou d’un projet « Cirque ». Il a aussi présenté des conférences sur le sujet et traduit une conférence de Colin Wright lors de la Nuit des Maths à Blois en 2017.
-
On observe que le nombre de chiffres ne correspond pas nécessairement au nombre de balles nécessaires pour la figure. Nous verrons ensuite comment ce dernier se détermine à partir du premier.↩
-
On a déjà vu un autre argument pour justifier que \(421\) ne se jongle pas, c’est que les lancers \(21\) arriveraient dans la même main en même temps.↩
-
Cela fera sans doute l’objet d’une suite dans la revue numérique d’Au fil des maths.↩


2 réflexions sur « Mathématiques du jonglage »
Les commentaires sont fermés.