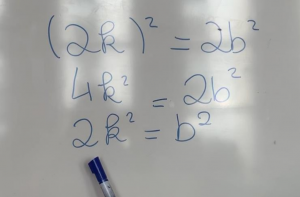Démontrer en vidéo
Comment travailler l’oral en mathématiques dans nos classes ? Les auteurs présentent ici une expérimentation menée en Seconde pendant l’année 2019-2020, autour de la démonstration et la création de vidéos par les élèves.
Christophe Hache & Étienne Quinchon
© APMEP Décembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Travailler l’oral en mathématiques ?
Des attentes institutionnelles
Les programmes du cycle 4 et du lycée mettent en avant six compétences dont une compétence « communiquer ». On trouve ainsi dans le programme de Seconde de 2019 [1] la compétence « communiquer un résultat par oral ou par écrit, expliquer une démarche ». La réforme du baccalauréat institue par ailleurs un « grand oral » dans lequel les mathématiques doivent trouver leur place.
Le travail oral individuel en classe est difficile. L’idée nous est donc venue d’un travail oral à distance à l’aide de vidéos. Un travail de fond sur l’oral favorise en effet l’apprentissage des mathématiques puisque l’expression orale incite les élèves à s’interroger explicitement sur leurs choix en termes de formulations. On retrouve cette idée par exemple dans le document « Mathématiques et maîtrise de la langue »[2]: « Ces différences entre oral et écrit peuvent être riches pour travailler la langue: chaque mode d’expression pouvant éclairer l’autre du fait même de leurs différences (d’autant plus si elles sont soulignées) ». De plus, l’oral a une part fondamentale dans le travail de conceptualisation. Le discours oral peut refléter davantage la construction du raisonnement des mathématiciens. « Les mathématiciens ne pensent pas à l’écrit » rappellent Katja Ploog et Sabine Bouveret [3] . Pour le justifier, elles comparent les rôles de l’oral et de l’écrit dans la démarche mathématique: « La différence majeure entre les deux modalités est donc leur lien au temps. L’objet texte est statique et reflète strictement l’ordre structurel des constructions; la linéarité écrite peut être « contournée » par la gestion visuelle du lecteur. À l’opposé, la linéarité de l’oral est inéluctable, et génère des formes qui reflètent le processus de construction en temps réel, avec tous les aléas liés à la construction en temps réel de l’idée émergente ». Dès lors, au-delà de l’intérêt de la pratique de l’oral dans la formation du scientifique et du citoyen, c’est aussi un argument cognitif qui conduit à donner une place importante à l’oral dans l’apprentissage des mathématiques. La pratique de l’oral est complémentaire de la pratique de l’écrit.
Le document d’accompagnement des programmes du cycle 4 sur la compétence « communiquer à l’écrit et à l’oral » [4] affirme que « la maîtrise de l’expression orale, au même titre que celle de l’écrit, constitue un objectif de formation à part entière. Cette maîtrise ne s’acquiert pas spontanément. Elle a ses spécificités et ne se limite pas à une transposition des compétences relevant de l’écrit ». Les enseignants sont donc invités à mettre en place des activités spécifiques permettant aux élèves de développer leur expression orale. « Une pédagogie de l’oral passe par des situations de communication offrant de vrais enjeux pour les interlocuteurs: s’expliquer, décrire, argumenter, convaincre, décider, etc. » [4]. Le programme évoque la participation orale des élèves pendant les cours, le travail en groupe (par exemple sur des problèmes ouverts permettant le débat contradictoire), la présentation de travaux, les questions flash. « L’oral apparaît comme un élément essentiel, comme le ciment commun de la classe, où tous les élèves sont ensemble pour avancer » [5].
En plus de ces premières pistes, peut-on imaginer d’autres méthodes de travail permettant aux élèves de développer leurs compétences d’expression orale ?
Différentes expérimentations s’appuyant sur des outils numériques
Sur le site de l’IREM de Paris, on peut ainsi trouver plusieurs vidéos réalisées par des collégiens[6] . Cette expérimentation a été travaillée par le groupe « Léo ». Les élèves (de 5e) devaient reformuler une propriété du cours (parallèles et perpendiculaires, droite des milieux, opérations sur les fractions) et la présenter oralement dans une courte vidéo en s’aidant essentiellement de post-it et de feutres. Ces vidéos constituent une forme de « bilan de savoir » [2]. Il s’agissait d’un travail de groupes réalisé pendant une heure de cours, le temps était donc limité, l’enseignante a filmé les différents groupes durant les dix dernières minutes de la séance.
Dans le même esprit, on trouve sur le site de l’académie de Versailles des vidéos également réalisées par des collégiens [7]. Il ne s’agit pas cette fois d’expliquer une propriété de cours mais de décrire des méthodes de constructions géométriques : construction de deux droites parallèles à la règle et à l’équerre ou en utilisant la symétrie centrale.
Sur le site de l’académie de Strasbourg, on trouve la description d’expérimentations relativement différentes [8], trace d’un atelier de formation animé par Katja Ploog et Sabine Bouveret [3]. Le travail s’appuie sur l’utilisation de fichiers MP3 pour « travailler l’oral et travailler à l’oral en mathématiques ». Il peut s’agir par exemple, dans le cadre d’une évaluation diagnostique, d’interviewer les élèves et d’enregistrer sur MP3 leurs productions orales. Il est également possible de proposer à des élèves de faire des exercices au format MP3 plutôt que par écrit. Ce type d’exercices peut notamment être mis en place dans le cadre des séances d’Accompagnement Personnalisé. Le bilan de ces différentes expériences est positif : « La baladodiffusion offre des opportunités nouvelles pour travailler l’oral et favoriser les échanges et la communication en mathématiques, en conservant la mémoire des productions » [8].
Nous présentons ici une expérimentation menée en Seconde pendant l’année 2019-2020 [9].
Évaluer l’oral en mathématiques ?
Après avoir souligné l’importance de développer les compétences d’expression orale des élèves et donné quelques exemples d’activités qui peuvent être mises en place, il est intéressant de réfléchir à l’évaluation de ces compétences.
Ainsi dans un document publié en septembre 2019 par l’académie de Versailles [10], il est affirmé que « la maîtrise de l’oral, au-delà des mathématiques, est aussi un enjeu majeur dans la formation de l’élève. Ce dernier doit avoir un retour sur sa pratique et l’enseignant doit donc l’évaluer. Cette évaluation se doit d’être formative, à la fois exigeante et bienveillante ». Les premières pistes esquissées pour favoriser le développement de compétences d’expression orale (participation orale, travaux de groupes, activités mentales ou flash) ne constituent pas un cadre évident pour une évaluation de ces compétences. Dans ce contexte, l’utilisation de fichiers MP3 ou vidéo peut s’avérer particulièrement pertinente afin de mettre en place une évaluation formative.
Une expérimentation centrée sur le travail hors classe mise en place dans l’académie de Paris et analysée sur son site internet [11] s’interroge sur la pertinence de cette forme de travail, notamment pour des élèves en difficulté. Par ailleurs, les professeurs de ce groupe de réflexion partent du constat suivant : « Évaluer l’oral n’est pas si courant en mathématiques. Les réticences des professeurs de mathématiques s’expliquent en partie par une culture du métier où ces pratiques sont assez périphériques et peu structurées. Elles tiennent également au temps que l’on peut consacrer en classe à ce type d’évaluation. On peut ajouter que, comme l’oral est souvent évalué à des moments différents et à partir de problèmes différents, on peut avoir l’impression de ne pas évaluer tous les élèves de la même façon » [11]. Des professeurs ont donc tenté des expérimentations de travaux hors la classe sous forme d’enregistrements audio et vidéo. Les élèves devaient par exemple présenter un compte-rendu oral de la résolution d’une équation (en 3e), ou expliquer la soustraction de nombres relatifs (en 5e). Le bilan de ces expérimentations est positif. Il montre d’une part que les élèves ont su s’auto-évaluer en faisant preuve d’une réelle exigence sur la qualité de leurs productions puisqu’ils n’ont pas hésité à s’enregistrer à plusieurs reprises. D’autre part, des élèves « très discrets en classe, se sont montrés très à l’aise dans la vidéo ». Enfin, au-delà du travail sur l’oral, ce format de devoir maison a incité les élèves à organiser leur travail et à recourir à l’utilisation de brouillons. Dans l’ensemble, leurs justifications étaient plus élaborées, ils ont pensé « à dire bien plus de choses à l’oral qu’à l’écrit ». Par ailleurs, ce travail publié par le rectorat de Paris cite certains critères d’évaluation : « qualités techniques (son et image), qualité de l’expression orale (clarté et niveau de langue), précision mathématique (précision des explications, du vocabulaire, et utilisation correcte des variables) » et la justesse du contenu mathématique.
La grille d’évaluation utilisée pour le cours de maths-sciences, en lycées professionnels, dans le cadre des Contrôles en Cours de Formation (CCF) est aussi très intéressante en ce qui concerne les pistes de critères d’évaluation de l’oral en mathématiques. En effet l’oral est systématiquement pris en compte dans les épreuves de maths-sciences pour les CAP et bacs professionnels. Rajàa Salah [12] liste certains critères retenus dans ce cadre : « Précision, clarté et structure de l’expression orale, pertinence dans l’argumentation et la réponse aux questions, qualité scientifique, technique et professionnelle du vocabulaire utilisé ».
Enfin, dans un document intitulé « La communication en classe de mathématiques » provenant du Ministère de l’Éducation de l’Ontario , on trouve plusieurs caractéristiques aidant les enseignants à évaluer leurs élèves : « Clarté de l’organisation des idées, qui vise à faciliter la compréhension du lecteur (qui ne doit pas avoir à inférer, ou très peu) », « Explications qui justifient les idées et stratégies mathématiques en s’appuyant sur un nombre suffisant d’éléments mathématiques significatifs », « Utilisation pertinente et précise de termes mathématiques, de symboles, de diagrammes et de schémas ».
Nous présentons ci-dessous la grille d’évaluation finalement adoptée pour notre expérimentation.
| Critères d’évaluation | TI* | I | S | TS | Appréciation | |
| Précision, clarté et structure de l’expression orale | /2 | |||||
| Pertinence du vocabulaire utilisé | /2 | |||||
| Rigueur, validité et cohérence du raisonnement | /2 | |||||
| Prise de recul par rapport à la démonstration, mise en valeur des points clés | /1 | |||||
| Utilisation pertinente d’un support | /1 | |||||
| Respect des consignes et des préconisations (tous les élèves s’expriment, la démonstration n’est pas lue, la vidéo dure entre 2 et 5 min…) | /1 | |||||
| Réalisation vidéo (image stable…) | /1 |
* TI=Très Insuffisant ; I=Insuffisant ; S=Satisfaisant ; TS=Très Satisfaisant.
Notre expérimentation : démonstration à l’oral au lycée
Le nouveau programme de mathématiques pour la classe de Seconde générale et technologique, entré en vigueur à la rentrée 2019 [1], insiste sur l’importance de la démonstration dans l’enseignement des mathématiques. Une quinzaine de démonstrations « exemplaires » figurent au programme. Il s’agit en fait d’une réponse aux recommandations du rapport Villani-Torossian [14] qui, même s’il n’évoque pas le travail oral des élèves, appelle à redonner une place significative à la présentation de démonstrations de résultats du cours. Le programme de Seconde générale et technologique invite à faire ce travail autour des démonstrations « selon des modalités variées ».
Compte tenu de tous les éléments qui précèdent, nous avons décidé d’expérimenter la production par les élèves, hors classe, de présentations orales filmées de démonstrations en Seconde. La préparation et la production se sont faites en groupes de deux à quatre élèves (les groupes ont été constitués librement sous la responsabilité des délégués pour que le travail puisse matériellement se faire de façon simple hors de la classe). Les contraintes exprimées concernant la production étaient les suivantes : tous les élèves doivent s’exprimer, la vidéo doit durer entre 2 et 5 minutes, les élèves ne doivent pas apparaître à l’image (l’image peut montrer des objets, des figures ou formules, de l’écrit de diverses natures, etc.). Des pistes ont été données aux élèves pour dynamiser la vidéo (format question réponse, utilisation de post-it, filmer un écran d’ordinateur…), mais ils étaient libres et pouvaient imaginer des idées originales pour rendre vivante la présentation de la démonstration. Il leur était clairement indiqué que le but de l’exercice n’était pas de se contenter de lire une démonstration. Un couplage de deux démonstrations qui figurent dans la liste ci-dessous a été attribué à chaque groupe (au choix du professeur). Les élèves ont pu alors en choisir une parmi les deux. Ces démonstrations avaient toutes été travaillées en classe avec les élèves en amont de ce projet :
-
Le nombre rationnel \(\frac{1}{3}\) n’est pas décimal.
-
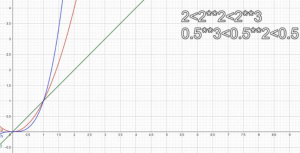
Étudier la position relative des courbes d’équations \(y = x\), \(y = x^{2}\) et \(y = x^{3}\), pour \(x \geqslant 0\).
-
Deux vecteurs sont colinéaires si et seulement si leur déterminant est nul.
-
Pour une valeur numérique de \(a\) (entier), la somme de deux multiples de \(a\) est multiple de \(a\).
-
Le carré d’un nombre impair est impair.
-
Le nombre réel \(\sqrt{2}\) est irrationnel.
La grille d’évaluation ainsi qu’une fiche descriptive donnant les consignes précises de l’activité ![]() ont été distribuées aux élèves en amont.
ont été distribuées aux élèves en amont.
Le temps donné aux élèves était relativement long (un mois). Voici le calendrier des principales étapes du projet :
- Lundi 3 février 2020
-
-
Présentation du travail demandé aux élèves. Visionnage de quelques exemples ne venant pas d’élèves de Seconde pour ne pas trop influencer le travail des élèves :
-
Remise de la fiche présentant l’activité et de la grille d’évaluation.
-
Constitution des groupes avant le jeudi.
-
- Jeudi 6 février 2020
-
Constitution définitive de la liste des groupes.
- Samedi 8 février 2020
-
Couplages de démonstrations attribués aux groupes.
- Samedi 14 mars 2020
-
Date limite de retour des fichiers mp4 (par clé USB ou via l’ENT). Le fichier pouvait être rendu plus tôt si le travail était terminé.
Pour chaque production, un retour a été fait par l’enseignant aux élèves concernés. Plusieurs suites possibles avaient été envisagées, mais n’ont pas pu avoir lieu cette année en raison de la crise sanitaire. Nous en présentons une synthèse dans les perspectives.
Analyse des productions des élèves
Au départ, lorsque le projet a été présenté aux élèves, la motivation était toute relative. Des travaux similaires avaient en effet déjà été demandés aux élèves dans d’autres disciplines. De plus, on peut penser que cette activité sortait les élèves de leurs habitudes, ce qui est inconfortable au départ. Ils se sont néanmoins investis avec beaucoup de sérieux dans ce travail. Dans l’ensemble, leurs productions sont en effet de qualité et le résultat d’un travail souvent approfondi. Il est certain qu’ils ont eu besoin de préparer minutieusement leurs enregistrements (organisation de la vidéo, choix du support, répartition des prises de parole…), et de s’entraîner sur l’expression orale. On peut penser que beaucoup de groupes se sont enregistrés à plusieurs reprises.
Sur les six démonstrations proposées aux élèves, une seule démonstration n’a jamais été choisie : « Pour une valeur numérique de \(a\) (entier), la somme de deux multiples de \(a\) est multiple de \(a\) ». Il s’agissait probablement de la démonstration la plus simple. Par ailleurs, les élèves se sont souvent orientés vers la démonstration la plus difficile de leur couplage. Il est possible que les élèves aient souhaité se lancer un défi. Il est également probable que la contrainte de temps (entre \(2\) et \(5\) minutes) les ait incités à choisir des démonstrations plus élaborées et donc plus longues.
Les démonstrations avaient toutes été traitées au préalable en classe, mais il subsiste des erreurs plus ou moins importantes. Dans l’ensemble les démonstrations sont cependant maîtrisées.
|
Exemples de supports vidéo.
Les élèves ont pris des initiatives dans la présentation : explications sur le type de raisonnement (absurde, réciproque), présentation du résultat sous forme d’une conjecture à partir d’un exemple avant la démonstration, introduction d’un exemple numérique en fin d’exposé pour illustrer la démonstration…
Les élèves étaient libres de choisir les supports de leur choix pour présenter leur démonstration. Ils ont opté pour des supports différents selon les groupes (du plus fréquent au moins fréquent : jeu de post-it, écriture sur tableau, écriture sur feuille, dépliage d’une feuille, diaporama, GeoGebra, représentation graphique sur papier quadrillé). Les choix les plus fréquemment faits ont été guidés par les exemples de vidéos proposés. Il paraît donc indispensable, de ce point de vue, de montrer des exemples variés aux élèves si l’on ne souhaite pas trop orienter leur travail. Pour certains choix, les élèves ont également fait preuve d’imagination !
On peut remarquer des liens entre qualité du support vidéo et qualité de l’expression orale. Un bémol sur un point : lorsque les supports étaient très rédigés, les élèves ont eu tendance à les lire, ce qui rendait la présentation moins vivante. Les supports contenant moins de formulations écrites ont donné lieu à des présentations orales plus élaborées. De manière générale, les élèves ont réellement cherché à adapter support vidéo et présentation de la démonstration pour en expliquer toutes les étapes. On peut alors penser que ce travail les a amenés à une compréhension plus approfondie de la démonstration. Par ailleurs, on trouve quelques erreurs mathématiques dans les supports, notamment pour des groupes qui ont écrit des passages de la démonstration pendant la vidéo.
Dans l’ensemble, les productions sont particulièrement satisfaisantes du point de vue de l’expression orale des élèves. Cette dernière est généralement de qualité tant sur le débit que sur la clarté des voix. On peut penser que la nouveauté de cet exercice et sa dimension orale inhabituelle ont incité les élèves à mettre l’accent sur cet aspect. Il est possible que plusieurs groupes aient rédigé au préalable un script. Peu d’élèves hésitent à l’oral. En outre, la majorité des groupes ont pensé de manière pertinente les changements de voix pour rendre plus claire la présentation. Certains utilisent un jeu de questions-réponses pour dynamiser leur propos. Quelques groupes n’ont cependant pas suffisamment cherché à reformuler et à expliquer leurs démonstrations, notamment dans les phases de calculs, certainement les plus difficiles à mettre en valeur à l’oral. D’autres groupes réussissent à bien reformuler leur démonstration, y compris les étapes de calculs, en expliquant clairement le passage d’une ligne à l’autre sans se contenter de lire : « passage au carré », « simplification », « factorisation », « développement ».
Enfin, les élèves ont souvent fait preuve d’une maîtrise satisfaisante du vocabulaire et des expressions usuelles en mathématiques. Certaines expressions sont utilisées alors qu’elles sont plus rares chez les élèves à l’écrit (« hypothèse », « conjecture », « disjonction des cas », « d’après la propriété », …). Leur usage n’est pas toujours maîtrisé, mais ceci peut être interprété comme le fait que les élèves semblent oser prendre davantage de risques à l’oral qu’à l’écrit. L’autocensure serait moins forte. Dans le cadre de ce travail, une consigne était particulièrement importante : tous les élèves devaient s’exprimer avec un bon équilibre des temps de parole. Cette consigne a été systématiquement respectée, ce qui a visiblement conduit chaque élève à s’investir. Les démonstrations étant variées, chacun a pu y trouver son compte. Le travail de groupes a aussi favorisé une entraide entre élèves. En cela, cette expérience confirme les conclusions de celle de l’académie de Paris : « Les « copies » des élèves en général, et des élèves en difficulté en particulier, ont plus de contenu à évaluer ». Ou encore, en comparant travail écrit et oral : « La tentation du mimétisme pur est alors très forte. À l’oral cette question du minimum à dire semble moins crispante, car il est plus facile et rapide de raconter ce qu’on a fait » [11]. Ces conclusions sont également partagées dans le compte rendu de l’académie de Strasbourg (travail avec MP3) : « Elle ouvre des pistes inédites pour l’évaluation, notamment dans le cadre du socle commun, et présente un intérêt majeur pour l’aide aux élèves en difficulté » [8].
Bilan et perspectives
Au terme de cette expérimentation et de ces analyses, il semble clair que la montée en compétences des élèves sur leur expression orale est un défi pour les professeurs de mathématiques. Les outils numériques, notamment audio et vidéo peuvent contribuer à favoriser ce travail. En particulier, la réalisation de courtes vidéos par des groupes d’élèves de Seconde pour présenter des démonstrations au programme, s’avère être une activité intéressante et ouvrant un éventail de possibilités.
Parmi les facteurs de réussite de l’expérimentation, soulignons ici le rôle de la première séance. Elle a un rôle central car ce travail était nouveau pour les élèves. Le descriptif de la consigne avait pour but de clarifier le travail à mener. La présentation des vidéos déjà existantes a permis de rassurer les élèves et les a aidés à se projeter dans leurs productions à venir, mais a aussi permis une première réflexion (collective) sur la nature de la vidéo à produire : chaque vidéo a fait l’objet de commentaires, de discussions. Dans cette mise en place un équilibre est à trouver : il faut à la fois cadrer le travail et laisser de la liberté (on a vu que les élèves savent s’en emparer, sur la forme et sur le fond).
Au vu de l’influence des vidéos données en exemples aux élèves, il aurait été intéressant d’en montrer une ou deux supplémentaires, pour ouvrir encore davantage de portes. Cela pourrait éventuellement nécessiter la création de vidéos en amont…Ou l’utilisation de vidéos d’élèves provenant d’autres classes (sur d’autres preuves).
Nous avons choisi de faire réaliser aux élèves les vidéos en dehors la classe, mais il peut être évidemment aussi envisagé de le faire en classe (pendant une heure d’accompagnement personnalisé par exemple, c’est ce qui avait été fait pour les vidéos de l’IREM de Paris [6]). Cela pourrait permettre une meilleure maîtrise de la composition des groupes de travail (ce qui peut être intéressant dans certains contextes) et du temps (temps écoulé entre le travail sur les démonstrations et la production des vidéos, entre la production des vidéos et le retour sur ce travail en classe, etc.).
Cette activité peut être approfondie en étant suivie d’étapes supplémentaires. Le premier approfondissement auquel on peut penser consisterait à faire visionner la vidéo d’un groupe par un autre groupe puis d’inviter les élèves à échanger sur leurs vidéos. Au vu de la qualité des analyses des élèves sur les vidéos montrées en exemple lors de la séance d’introduction de l’activité, cet approfondissement serait sûrement riche pour les élèves. D’une part, ils pourraient ainsi entendre un retour sur leur travail provenant d’autres élèves, ce qui n’est pas la même chose qu’un retour provenant de leur professeur. D’autre part, il leur faudrait prendre la posture d’observateur, ce qui est très intéressant, notamment pour apprendre à déceler d’éventuelles erreurs dans les démonstrations. Les élèves apprendraient ainsi à adopter aussi bien la posture d’auteur/orateur que la posture d’observateur/auditeur. On peut faire le parallèle avec le lien fondamental entre posture d’auteur et de lecteur souligné par les didacticiens du français. « On attend de l’élève-auteur qu’il ait une intention, notamment vis-à-vis du lecteur, qu’il soit conscient des effets produits (ou au moins du fait que son texte aura des effets sur le lecteur, doit avoir un effet), qu’il ait une stratégie d’écriture, du recul sur son activité d’écriture et son écrit » [16].
Un autre approfondissement possible serait alors de refaire le lien avec l’écrit après cet exercice oral. Par exemple, les élèves sont-ils capables de rédiger la démonstration sur laquelle ils ont travaillé ? Ou plus difficile peut-être : les élèves sont-ils capables de rédiger la démonstration choisie par un autre groupe après avoir visualisé leur production ? « Si l’une et l’autre recouvrent des compétences spécifiques, la maîtrise de l’oral et celle de l’écrit sont liées entre elles et le travail réalisé en faveur de l’une peut être réinvesti au service de l’autre » [4]. Ce réinvestissement peut s’avérer relativement complexe et il nécessite donc un travail régulier. Comme le soulignent Katja Ploog et Sabine Bouveret, « il est primordial de comprendre que l’écrit n’est pas une copie symétrique de l’oral, et que, en conséquence, la transposition d’un message oral vers l’écrit relève d’un calcul mental à part entière » [3]. On pourrait alors imaginer de répéter l’exercice à plusieurs reprises dans l’année (par exemple une fois par trimestre ou une fois par période) : en début d’année sur des démonstrations relativement simples, et plus tard dans l’année sur des démonstrations plus difficiles. Les élèves pourraient ainsi acquérir des automatismes et apprendre à dépasser un certain nombre de difficultés rencontrées au cours des premières réalisations. Cela permettrait en outre d’exploiter davantage les allers et retours entre oral et écrit, et entre posture d’auteur/orateur et posture d’observateur/auditeur. Les productions s’enrichiraient les unes les autres et feraient potentiellement naître de nouvelles idées aux élèves. Forts de ces expériences successives, ils pourraient ainsi monter en compétences au fil de l’année.
Références :
-
Ministère de l’Éducation nationale. Programme de mathématiques de Seconde générale et technologique.
 2019
2019 -
Ministère de l’Éducation nationale de l’Enseignement supérieur et de la Recherche. Mathématiques et maîtrise de la langue.
 2016
2016 -
K. Ploog et S. Bouveret. « Apprendre avec l’oral et à l’oral ». In : Au fil des Maths n°531
 2019
2019 -
Ministère de l’Éducation nationale de l’Enseignement supérieur et de la Recherche. Communiquer à l’écrit et à l’oral.
 2016
2016 -
F. Leguelinel et A. Monfront. « Faire circuler la parole en classe ». In : PLOT n°51 pp 12-13
 2015
2015 -
Groupe Léo. Reformulation vidéo. Publication en ligne de l’IREM de Paris .
 2015.
2015. -
Académie de Versailles. Les vidéos géométriques du collège Les Molières : épisode 3.
 2015.
2015. -
Académie de Strasbourg. Utiliser un MP3 pour travailler l’oral et travailler à l’oral en mathématiques. Des pistes nouvelles pour la construction des apprentissages et l’évaluation. Interacadémiques de Mulhouse.
 2013
2013 -
É. Quinchon. Développer les compétences d’expression orale à l’aide de vidéos. À paraître sur INSPÉ de Paris, Sorbonne Université.

-
Académie de Versailles. Rentrée mathématique. L’oral en mathématiques.
 Septembre 2019.
Septembre 2019. -
Académie de Paris. Travail hors la classe : productions audio et vidéo.
 2019.
2019. -
R. Salah. « La place de l’oral dans l’enseignement des mathématiques en Lycée professionnel ». In : PLOT n° 53 (2016).pp. 14-18.

-
Ministère de l’Éducation de l’Ontario. La communication en classe de mathématiques.
 2011.
2011. -
C. Villani et C. Torossian. 21 mesures pour l’enseignement des mathématiques.
 2018.
2018. -
Exo7. Correction vidéo de l’exercice 7 de la feuille d’exercice du chapitre « Arithmétique » de première année.
 2010.
2010. -
C. Hache. Questions langagières dans l’enseignement et l’apprentissage des mathématiques. Note de synthèse HdR.
 Université Paris Diderot, 2019.
Université Paris Diderot, 2019.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Christophe Hache est maître de conférence à l’UFR de mathématique de l’Université de Paris. Il coordonne aussi le travail de deux groupes de l’IREM (« Léo, langage, écrit, oral » et « Démontrer »).
Étienne Quinchon est professeur de mathématiques au collège Claude-Nicolas Ledoux au Plessis-Robinson (académie de Versailles). Lorsqu’il a mené l’expérimentation décrite dans cet article, il enseignait au lycée Carnot à Paris.