Dessous de table

Vous avez sûrement déjà visionné à maintes reprises la vidéo La face cachée des tables de multiplication de Launay et vous ne vous en lassez pas
Anne-France Acciari et Mathias Zessin nous dévoilent la face cachée de cette vidéo en explicitant certaines des propriétés mathématiques sous-jacentes.

Anne-France Acciari et Mathias Zessin

© APMEP Mars 2018

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Avec plus de deux millions de vues, la vidéo La face cachée des tables de multiplication de Mickael Launay est un véritable succès sur l’internet.

À quoi tient ce succès ? Peut-être à l’association des tables de multiplication, mauvais souvenir des leçons de mathématiques pour beaucoup, et de la beauté des courbes que l’on peut admirer. Nul besoin de faire des études poussées en algèbre pour avoir appris les tables de multiplication et nul besoin d’avoir des connaissances en art pour être sensible aux magnifiques courbes associées. Mais comment expliquer que des courbes si belles et symétriques apparaissent juste en reliant quelques points d’un cercle selon les tables de multiplication ?

Nous allons nous limiter dans cet article au cas de la table de 2 et à son lien avec une courbe bien connue : la cardioïde. Les résultats se généralisent aisément pour certains nombres plus élevés.

Illusion d’optique

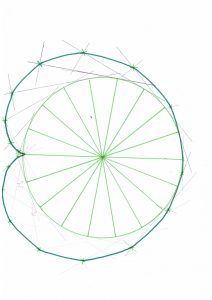
Pour tout entier n, nous appellerons figure de la multiplication par 2 modulo n, la figure obtenue en positionnant les entiers de 0 à n − 1 sur le cercle unité et en reliant chaque entier à son double modulo n. On s’intéresse au phénomène observé lorsqu’on augmente la valeur de n. Une courbe étrange semble apparaître. Elle ressemble bien à une carcinoïde.

Nous allons démontrer que c’est bien le cas et qu’elle apparaît de la manière suivante : les segments tracés sont tous tangents à la cardioïde. C’est cette propriété qui est à la base de l’illusion d’optique observée.

Figure 1 : Table de 2 modulo 22, 36 et 57.

Étude du cercle unité

On considère que le cercle de la figure est le cercle unité du plan complexe.

Le nombre 0 sera situé au point d’affixe 1 et les nombres de 1 à n − 1 seront disposés régulièrement sur le cercle dans le sens trigonométrique.

Démontrons dans un premier temps qu’à tout point du cercle unité correspond un unique point de la figure, indépendamment de n. Illustrons ceci par l’exemple ci-dessous. On pourra alors donner à n la valeur qu’on souhaite, afin d’avoir un nombre suffisant de points et que se dégage une jolie courbe.

Soit \(k \in [1 ; n-1]\). L’affixe de la position du nombre k est alors \(\exp(\mathrm{i} \theta)\), avec \(\theta = \frac{2k\pi }{n}\cdotp\) L’affixe de la position du nombre 2k est alors \(\exp(2 \mathrm{i}\theta)\).

Si on fait varier n, un même point du cercle peut être l’image d’un nombre k modulo n et d’un nombre kʹ modulo nʹ (voir exemple ci-contre). Le point auquel il sera relié est le même, que l’on raisonne avec n ou nʹ. En effet, ces points ont une affixe de même argument θ et l’argument des affixes des points correspondant à 2k et 2kʹ sera donc égal à 2θ.

On a alors montré que l’image d’un point par l’opération multiplication par 2 ne dépend pas du n choisi, c’est-à-dire du nombre de points sur le cercle.

On en déduit qu’on peut, en un certain sens, faire tendre n vers  + ∞ et obtenir une figure où chaque point d’affixe \(\exp(\mathrm{i}\theta)\) est relié à un point du cercle d’affixe \(\exp(2 \mathrm{i} \theta)\).

On s’affranchit maintenant du n et on considère l’ensemble des points du cercle unité.

La cardioïde

De façon générale, une cardioïde est un ensemble que l’on peut paramétrer de la façon suivante: \(C=\left\{(x(\theta)\,;\,y(\theta)),\ \theta \in ]-\pi ; \pi]\right\}\) avec

$$\begin{aligned}
x(\theta) & = a \cos(\theta) (1+ \cos(\theta)) + b \\
y(\theta) & = a \sin(\theta) (1+ \cos(\theta)) + c
\end{aligned}$$

où a, b et c sont des nombres réels.

Pour chaque valeur du paramètre θ, nous noterons M_θ le point de C correspondant. Et nous noterons A_θ le point du cercle unité de coordonnées (cos(θ) ;  sin(θ)).

Lorsqu’une courbe donnée est paramétrée sous la forme (x(θ) ;  y(θ)), θ variant dans \(\mathbb{R}\), le vecteur (xʹ(θ) ;  yʹ(θ)) est un vecteur tangent à la courbe au point de coordonnées (x(θ) ;  y(θ)) considéré.

Détermination des paramètres de la cardioïde

Nous supposons maintenant que la figure que l’on voit apparaître à l’intérieur du cercle est bien une cardioïde et que chaque segment de la figure de multiplication par 2 est tangent à cette carcinoïde.

Déterminons maintenant les paramètres de la cardioïde qui nous intéresse.

La cardioïde recherchée est symétrique par rapport à l’axe des abscisses. On obtient une telle symétrie si l’abscisse x est une fonction paire et l’ordonnée y est une fonction impaire. C’est le cas si et seulement si c est nul.

Nous appellerons sommet de la cardioïde l’unique point de rebroussement que l’on peut voir sur la courbe. Ce sommet se trouve sur l’axe des abscisses et le vecteur tangent à la courbe est horizontal en ce point.

Déterminons ses coordonnées.

Le vecteur tangent est horizontal quand yʹ(θ) = 0. Des calculs permettent de trouver que c’est le cas pour trois valeurs de θ: π, \(\frac{\pi}{3}\) et \(-\frac{\pi}{3}\cdotp\) En se référant au dessin et à la symétrie de la courbe ou par détermination du point de rebroussement par le calcul, le sommet est alors M_π et ses coordonnées sont (b ;  0). De plus, \(M_{\frac{\pi}{3}}\) est le point le plus haut et \(M_{-\frac{\pi}{3}}\) est le point le plus bas de la carcinoïde.

Le segment [A_θA_2θ] est horizontal lorsque les points A_θ et A_2θ sont distincts et ont la même ordonnée, c’est-à-dire quand sin(θ) = sin(2θ) et ceci est vérifié pour trois valeurs de θ : \(\frac{\pi}{3}\), \(-\frac{\pi}{3}\) et π. En considérant que les points du paragraphe précédent sont les points de tangence de ces trois segments à la courbe et en classant les ordonnées, on obtient que \(M_{\frac{\pi}{3}}\) se trouve sur le segment \(\left[A_{\frac{\pi}{3}}A_{\frac{2\pi}{3}}\right] \) et \(M_{-\frac{\pi}{3}}\) sur le segment \(\left[A_{-\frac{\pi}{3}}A_{-\frac{2\pi}{3}}\right]\). Les points
$$M_{\frac{\pi}{3}} \left(\frac{3}{4}a+b\,;\,\frac{3
\sqrt{3}}{4}a\right) \text{ et } A_{\frac{\pi}{3}} \left(\frac{1}{2}\,;\,\frac{
\sqrt{3}}{2}\right)$$
doivent alors avoir la même ordonnée, et on obtient \(a = \frac{2}{3}\cdotp\)

De même, le vecteur tangent est vertical quand xʹ(θ) = 0.

Et ceci est vérifié pour quatre valeurs de θ: 0, \(-\frac{2\pi}{3}\), \(\frac{2\pi}{3}\) et π. Le segment [A_θA_2θ] est vertical lorsque les points A_θ et A_2θ ont la même abscisse, c’est-à-dire lorsque cos(θ) = cos(2θ) et ceci est vérifié pour trois valeurs de θ : 0, \(-\frac{2\pi}{3}\) et \(\frac{2\pi}{3}\cdotp\) Les points
$$M_{\frac{2\pi}{3}} \left(-\frac{1}{4}a+b\,;\,\frac{\sqrt{3}}{4}a
\right) \text{ et } A_{\frac{2\pi}{3}}
\left(-\frac{1}{2}\,;\,\frac{\sqrt{3}}{2} \right)$$
doivent avoir la même abscisse et \(a = \frac{2}{3}\), donc \(b = -\frac{1}{3}\cdotp\)

La cardioïde cherchée est donc l’ensemble :

$$C = \left\{\left(\frac{2}{3}\cos(\theta)(1+\cos(\theta))-\frac{1}{3}\,;
\,\frac{2}{3}sin(\theta)(1+\cos(\theta))\right)\right\}$$
avec \(\theta \in ]-\pi ; \pi]\).

Expliquons pourquoi la courbe obtenue est bien une cardioïde

Voyons maintenant pourquoi les segments tracés sont tous tangents à la cardioïde déterminée dans la partie précédente.

Soit \(\theta \in \mathbb{R}\). En calculant les affixes des vecteurs \(\overrightarrow{A_{\theta}M_{\theta}} \) et \(\overrightarrow{A_{2\theta}M_{\theta}}\), on démontre que les points A_θ, M_θ et A_2θ sont alignés. En effet  :

$$\begin{aligned}
\overrightarrow{A_\theta M_\theta} &
\begin{pmatrix}
\frac{2}{3}
\cos(\theta)(1+\cos(\theta))-\frac{1}{3}
-\cos( \theta)
\\[10pt]
\frac{2}{3}\sin(\theta)(1+\cos(\theta))
-\sin(\theta)
\end{pmatrix}\\
\overrightarrow{A_\theta M_\theta} &
\begin{pmatrix}
-\frac{1}{3}
\cos(\theta)+ \frac{2}{3}\cos^2(\theta)-\frac{1}{3}
\\[10pt]
\frac{2}{3}\sin(\theta)\cos(\theta)-\frac{1}{3}\sin(\theta)
\end{pmatrix}\end{aligned}$$
$$\begin{aligned}
\overrightarrow{A_{2\theta} M_\theta} &
\begin{pmatrix}
\frac{2}{3}
\cos(\theta)(1+\cos(\theta))-\frac{1}{3}
-\cos(2\theta)
\\[10pt]
\frac{2}{3}\sin(\theta)(1+\cos(\theta))
-\sin(2\theta)
\end{pmatrix}\\
\overrightarrow{A_{2\theta} M_\theta} &
\begin{pmatrix}
\frac{2}{3}
\cos(\theta)(1+\cos(\theta))-\frac{1}{3}
-2\cos^2(\theta)+1
\\[10pt]
\frac{2}{3}\sin(\theta)(1+\cos(\theta))
-2\sin(\theta)\cos(\theta)
\end{pmatrix}\\
\overrightarrow{A_{2\theta} M_\theta} &
\begin{pmatrix}
\frac{2}{3}
\cos(\theta)- \frac{4}{3}\cos^2(\theta)+\frac{2}{3} \\[10pt]
-\frac{4}{3}\sin(\theta)\cos(\theta)+\frac{2}{3}\sin(\theta)
\end{pmatrix}\end{aligned}$$

Donc \(\overrightarrow{A_{2\theta} M_\theta} = -2 \overrightarrow{A_{\theta} M_\theta}\).

De plus en comparant la pente de la droite (A_θA_2θ) à celle du vecteur tangent à la cardioïde en M_θ, on se rend compte qu’elles sont égales.

Calculons m_θ, la pente de la droite (A_θA_2θ) :

$$m_\theta = \frac{\sin(2 \theta)-sin(\theta)}
{\cos(2 \theta) -\cos(\theta)}\cdotp$$

Calculons p_θ, la pente du vecteur tangent à la cardioïde en M_θ :

$$\begin{aligned}
p_\theta & = \frac{y'(\theta)}{x'(\theta)} \\
&= \frac{
\left(\frac{2}{3}\sin(\theta)(1+\cos(\theta)\right)’}
{\left(\frac{2}{3}\cos(\theta)(1+\cos(\theta))-\frac{1}{3}\right)’}\\
& =\frac{\frac{2}{3}
\left(\cos(\theta)(1+\cos(\theta))+\sin(\theta)(-\sin(\theta))\right)}
{\frac{2}{3}\left(-\sin(\theta)(1+\cos(\theta))+\cos(\theta)(-\sin(\theta))\right)}\\
& = \frac{\cos(2 \theta)+\cos(\theta)}{-\sin(2 \theta)- \sin(\theta)}\cdotp\end{aligned}$$

En vérifiant que les produits en croix sont égaux, on montre aisément l’égalité des quotients.

On a alors m_θ = p_θ, les deux pentes sont égales. On en déduit que le segment \([A_\theta ; A_{2 \theta}]\) est tangent à la cardioïde au point M_θ.

Compléments

La cardioïde est une courbe apparaissant naturellement dans un bon nombre de phénomènes. Le joli site Mathcurve  les recense.

La façon de construire une cardioïde que nous étudions ici est dite « de Crémona ». Elle correspond à l’enveloppe des cordes [PQ], où P et Q sont deux points parcourant le cercle dans le même sens, l’un allant deux fois plus vite que l’autre.

Parmi les propriétés de la cardioïde, on remarque également qu’elle est une épicycloïde: on peut l’obtenir en faisant rouler un cercle de rayon 1 à l’extérieur d’un cercle de rayon 1 et en observant la trajectoire d’un point du petit cercle. Les figures observées dans la vidéo sont obtenues en ne considérant plus seulement la multiplication par 2 mais les multiplications par des entiers k de plus en plus grands. On reconnaît (au moins pour des petites valeurs de k) l’épicycloïde obtenue en faisant rouler le cercle de rayon \(\frac{1}{k}\) à l’extérieur d’un cercle de rayon 1. La propriété étudiée ici semble donc se généraliser.

La cardioïde peut être tracée de multiples façons, et on peut la faire construire par des élèves de 6, notamment dans le cas n = 36.

Anne-France Acciari est enseignante au collège Nelson Mandela à Illkirch et Mathias Zessin à l’INSA à Strasbourg. Ils se sont inspirés, pour cet article, d’un devoir maison donné aux étudiants de l’INSA par Jean-Romain Heu.

---