Le jeu Al-Jabr : le bonheur est dans les dés !

Comment faire vivre l’algèbre par l’intermédiaire d’un jeu ? Les auteurs présentent ici le jeu Al-Jabr, qu’ils ont mis au point pour des collégiens durant l’été 2018…

Olivier Garrigue, Ricardo Lima & Jorge Rezende

© APMEP Mars 2021

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Le jeu Al-Jabr a vu le jour alors que nous menions une réflexion sur l’enseignement de l’algèbre au collège dans notre groupe de l’IREM d’Aix-Marseille .

Nous pourrions évoquer toutes les raisons énoncées entre autres par Éric Trouillot dans le numéro 535 d’Au fil des maths pour motiver l’utilisation de jeux dans l’apprentissage des mathématiques. Mais nous ne retiendrons ici qu’un point qui nous paraît essentiel : le jeu facilite les échanges entre les élèves mais aussi avec le professeur et les élèves s’expriment sans appréhension sur un sujet qui peut en rebuter plus d’un. De plus, c’est par le biais du jeu que les élèves peuvent développer des compétences orales et plus précisément des habilités de communication, notamment dans le cadre d’un travail sur l’algèbre.

Si dans un premier temps nous présentons le jeu Al-Jabr et les différentes possibilités de le mettre en œuvre, nous terminons, dans un second temps, par quelques remarques sur les expérimentations que nous avons pu mener avec les élèves.

Qu’est-ce que le jeu Al-Jabr ?

Le jeu Al-Jabr que nous avons créé est constitué de différentes familles de cartes à jouer : la famille « \(x\) » en bleu, la famille « \(y\) » en rouge, la famille « \(z\) » en vert vif, la famille « \(t\) » en orange, la famille « \(u\) » en vert kaki, la famille « \(v\) » en mauve et la famille « \(a\) » en jaune. Chaque famille est composée de dix cartes, chaque carte a son recto en couleur avec une expression algébrique et son verso sur fond blanc avec le graphique correspondant à l’expression algébrique.

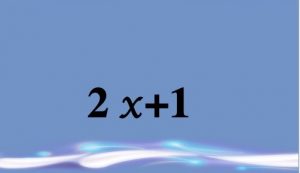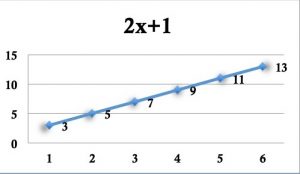Recto d’une carte de la famille x.	Verso de la carte.

Si nous regardons les familles en détail, voici succinctement ce que nous avons :

Famille \(x\) :

Fonctions linéaires croissantes. Pente de 1 ou 2.

Famille \(y\) :

Fonctions linéaires croissantes. Pente de 3 ou 4. S’y glisse une fonction constante.

Famille \(z\) :

Fonctions linéaires croissantes, constantes et décroissantes.

Famille \(t\) :

Fonctions linéaires croissantes et décroissantes. Une même fonction croissante représentée par 4 formules « vraies jumelles » (nous reviendrons sur cette notion dans le paragraphe 3), une fonction décroissante représentée par 5 formules « vraies jumelles » et un intrus.

Famille \(u\) :

Fonctions linéaires croissantes et décroissantes. Trois fonctions croissantes représentées pour chacune d’elle par 3 formules « vraies jumelles » et un intrus.

Famille \(v\) :

Une seule fonction linéaire croissante représentée par 10 formules « vraies jumelles ».

La Famille \(a\) n’est pas droite !

Elle est constituée de 10 fonctions polynômes de degré 2.

Les cartes, une notice explicative et quelques diapositives que l’enseignant peut utiliser sont disponibles (en fichier au format pdf) .

Pour jouer il faut se munir des cartes préalablement plastifiées et de « dés de 6 ».

Quelles sont les différentes règles que nous pouvons appliquer au jeu Al-Jabr ?

Plusieurs jeux sont possibles.

Jeu simple avec une famille

Jeu simple avec une famille.

• On choisit une famille, on bat les cartes, on les pose sur la table avec la face en couleur des formules visible.

• On pioche d’abord la carte qui est dessus.

• Chaque joueur (ou équipe) lance son dé.

• Chaque joueur (ou équipe) calcule la valeur de la formule de la carte avec le nombre qu’il a tiré avec son dé.

• On vérifie si chaque calcul est juste en regardant le dos de la carte.

  Exemple : carte \(2(x + 1)\), dé obtenu : 5, points obtenus : 12.

• Si le calcul est juste on note le nombre de points gagnés par le joueur, sinon on ne lui attribue aucun point.

• Chacun note ses points.

• On continue une carte après l’autre jusqu’à terminer la famille.

• Le gagnant (ou l’équipe gagnante) est celui qui a le plus de points à la fin de la partie.

Jeu simple avec plusieurs familles

On mélange les cartes de plusieurs familles et on joue comme avec une famille.

Jeu de bataille (avec une ou plusieurs familles)

• On bat les cartes.

• On distribue les cartes aux joueurs.

• Pour commencer, chaque joueur fait un paquet de ses cartes sans les ordonner et sans les regarder.

• Le premier joueur met sur la table la première carte de son paquet côté formule en vue, le second fait la même chose. Chaque joueur jette le dé et calcule ses points. On vérifie avec le graphe.

• Celui qui a le plus de points prend les 2 cartes. On dit « bataille » quand les 2 joueurs ont les mêmes points. Dans ce cas, on rejoue chacun une autre carte. Le gagnant remportera les 4 cartes.

• Le gagnant d’une partie est celui qui aura en mains toutes les cartes du jeu.

Le but est que les élèves se saisissent complètement de ces cartes et inventent un jeu avec des règles qu’ils auront mises en place d’un commun accord avec le joueur (l’équipe) adverse. Ainsi nos élèves ont, par exemple, mis en place les deux jeux suivants.

« La Bataille Défis du collège La Carraire de Miramas »

Le concept est simple et reprend le jeu simple avec plusieurs familles. C’est l’équipe adverse qui choisit la carte, c’est-à-dire : « Lorsque l’équipe 1 doit lancer le dé, l’équipe 2 choisit la carte avec laquelle l’équipe 1 compte ses points ; lorsque c’est à l’équipe 2 de lancer le dé, c’est l’équipe 1 qui choisit la carte ; et ainsi de suite. »

Avec une telle règle, « les défis sont plus grands », les élèves (les équipes) ne s’entraident plus et ils utilisent des stratégies : si l’élève qui compte éprouve des difficultés, ils lui donnent « une carte dure » en espérant qu’il se trompe et qu’il rapporte 0 point à son équipe. Sinon ils donnent des cartes qui rapportent le moins de points possible. Certains élèves vont jusqu’à essayer d’anticiper les cartes.

« Le Jeu du Totem-Matheux (Lucie®) »

Ce jeu se joue à 2 joueurs minimum (équipes possibles).

On utilise autant de familles que l’on veut.

Il faut un « Totem » (un tube de colle peut faire l’affaire !)

• Un des joueurs, à tour de rôle, lance un dé et tous les joueurs doivent calculer le résultat correspondant à la première carte de la pioche selon le nombre du dé.

• Le premier à prendre le Totem TOUT EN DISANT LE RÉSULTAT DU CALCUL gagne la carte s’il a donné le bon résultat. Il met la carte dans ses « cartes gagnées ».

• S’il donne un mauvais résultat, il remet dans la pioche une de ses « cartes gagnées » plus la carte jouée.

• Si deux joueurs attrapent le Totem et donnent le bon résultat en même temps, c’est celui qui a le plus de doigts sur le Totem qui emporte la carte. S’ils ont le même nombre de doigts c’est celui qui a la main la plus basse.

• Lorsque toutes les cartes de la pioche ont été jouées, chaque joueur/équipe compte ses cartes gagnées, celui/celle qui en a le plus gagne la partie.

Le jeu Totem : « on commence par les bleues pour s’échauffer et après on prend d’autres couleurs ».

Quelles sont les autres possibilités avec le jeu Al-Jabr ?

Nous remarquerons que chaque famille a des caractéristiques bien précises indépendamment des règles du jeu que nous pouvons mettre en place. Ainsi, au départ, nous pouvons établir, avec les élèves, le vocabulaire suivant qui pourra être amélioré par la suite en fonction de l’évolution des connaissances des élèves sur les expressions littérales :

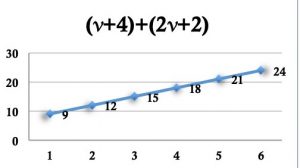
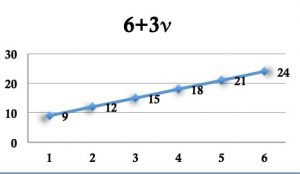
• deux cartes seront dites « vraies jumelles » si leurs formules différentes représentent la même fonction ;

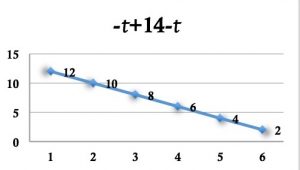
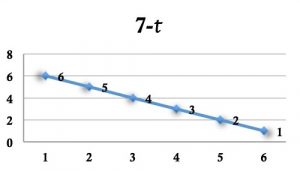
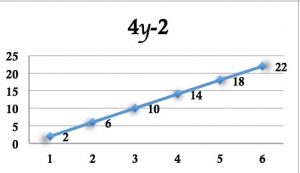
• deux cartes seront dites « fausses jumelles » si leurs graphes « semblent » identiques mais ne le sont pas (en attirant l’attention sur les unités utilisées sur les axes des ordonnées). Cette activité contribue à développer la capacité des élèves à lire des graphiques.

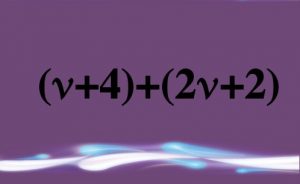Exemple de cartes dites « vraies jumelles ».
Exemple de cartes dites « fausses jumelles ».

« Elles se ressemblent, elles vont toutes les deux vers le bas, mais ce n’est pas les mêmes valeurs. . . » (élève de Cinquième).

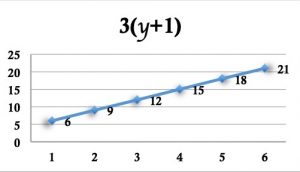
Exemple de cartes dites « vraies jumelles ».

« Les axes sont identiques, les droites montent toutes les deux et les valeurs sont presque pareilles, on peut se faire avoir. » (élève de Quatrième).

Dans chaque famille, nous pouvons poser la question « vraies ou fausses jumelles ? », ou alors nous pouvons tout simplement suggérer aux élèves d’analyser les familles par équipe avec comme prétexte d’élaborer des stratégies.

Après une première partie de cartes, les élèves se lancent dans une étude de la famille des \(x\).

Quelques mots sur notre expérimentation du jeu Al-Jabr

Il faut tout d’abord préciser que nous avons utilisé ce jeu à plusieurs niveaux d’enseignement et dans différentes circonstances. C’est-à-dire, aussi bien avec des élèves de Cinquième, de Quatrième que de Troisième (dispositifs mis en place pour une classe ou un groupe d’élèves) qu’avec des élèves de niveaux mêlés lors de « rencontres mathématiques » organisées à l’occasion de la semaine des mathématiques, mais aussi à l’occasion de la finale académique de « Maths sans frontières » et .

De notre point de vue, lorsque nous abordons l’enseignement de l’algèbre, le symbolisme et les règles de calculs algébriques parfois trop prégnants sont une source importante de démotivation pour beaucoup d’élèves. Utiliser le biais de ce jeu et privilégier la verbalisation du calcul d’une valeur d’une expression algébrique peut permettre de rendre leur approche plus légère et ainsi proposer une alternative pour palier à cette démotivation. En effet, nous avons constaté que les élèves se lancent sans retenue dans le jeu. Malgré leurs difficultés, ils n’ont pas peur de la compétition, ils la réclament même souvent.

Une particularité du jeu Al-Jabr est aussi de montrer aux élèves qu’en mathématiques, des graphiques, des tableaux de valeurs sont parfois plus efficaces pour la compréhension que des longs discours. Ces outils permettent de regrouper un nombre important d’informations et la richesse des expressions algébriques se révèle alors plus facilement aux élèves. En effet, nous nous sommes aperçus que l’information graphique présentée au verso des cartes était lue unanimement et rapidement sans équivoque par les élèves, contribuant ainsi à leur confiance en la compréhension du sujet.

Au début de l’expérimentation, nous avons pu voir que, dans un premier temps, les élèves s’entraident, partenaires comme adversaires, afin de partir sur un pied d’égalité ou pour mieux aguerrir les coéquipiers : « Je t’explique comment on fait pour calculer avec cette expression, après on relance le dé. » En revanche, dans un second temps, ils n’hésitent pas à durcir les règles du jeu avec des limites de temps ou des pertes de points, à utiliser des stratégies amenant l’adversaire à l’erreur, etc.

Le jeu facilite la communication entre les élèves, ils parlent, ils s’entraident, ils expérimentent des règles du jeu, ils débattent sur les différentes expressions algébriques et découvrent des stratégies de plus en plus élaborées : « Pour ces cartes, si tu réduis l’expression avant de calculer tu gagnes du temps » ; « […] là, dans cette famille, les expressions, tu t’aperçois en fait que c’est toutes les mêmes, c’est toujours les mêmes résultats, t’as qu’à développer, tu verras […] ». Les parties qui se déroulent avec ce jeu permettent petit à petit à l’élève de mieux maîtriser le registre de langage adapté à l’apprentissage de l’algèbre.

Du point de vue de l’élève, savoir expliquer à ses camarades devient un enjeu. Ainsi, comme nous l’avons évoqué en introduction, les élèves développent des compétences au niveau de l’oral. En effet, l’élève doit tour à tour : savoir écouter et mémoriser, savoir reformuler, savoir vérifier auprès de ses camarades s’ils ont bien compris, savoir développer un point de vue, une argumentation et expliquer. Si le langage employé par les élèves n’est pas forcément celui qui doit être institutionnalisé, les élèves prennent peu à peu conscience qu’il existe un langage « courant » et un langage plus « codifié » qui est celui de l’algèbre avec un champ lexical particulier. Pour ce dernier, d’ailleurs, de nombreux termes sont ambivalents, ils ont un sens en algèbre qui n’est pas forcément le même que dans le langage courant : « développer », « réduire », « facteur », etc.

Du point de vue de l’enseignement, nous pouvons dire qu’au niveau de tout apprentissage et en particulier au niveau de celui de l’algèbre, l’explication du professeur est parfois trop en décalage avec le niveau de compréhension de l’élève (à cause du vocabulaire employé par le professeur, à cause de la syntaxe qu’il utilise et bien d’autres paramètres encore qui peuvent être liés à la transmission orale). L’intérêt de passer par ce jeu est alors de recentrer les explications orales sur les expressions algébriques au niveau des élèves car ce sont eux-mêmes qui s’y emploient. Il est bien entendu que le professeur veillera à maîtriser de trop grandes dérives langagières pour permettre à l’élève de se rapprocher du langage plus codifié employé pour l’étude des expressions algébriques. Il ne faut, toutefois, pas perdre de vue qu’un élève qui s’exprime mal ou de manière laborieuse ou encore un élève plus introverti qu’un autre n’est pas nécessairement un élève qui a des difficultés en mathématiques. Le jeu pourra en revanche lui permettre de se mêler plus facilement aux échanges avec les autres.

Au sujet de notre expérimentation, nous avons pu enfin remarquer que les élèves se plient par la suite plus volontiers à un travail écrit sur les expressions algébriques. Soulignons d’ailleurs que pour appuyer leurs explications orales, les élèves éprouvent naturellement le besoin de passer par l’écrit. C’est souvent à ce niveau que les élèves prennent du recul sur le langage spécifique à l’algèbre. Les expressions algébriques sont ainsi analysées avec plus d’objectivité mais surtout moins d’appréhension…

Conclusion

L’utilisation de ce jeu durant ces dernières années nous a permis de mieux apprécier la qualité et l’apport des échanges durant les phases de jeu où les élèves éprouvent une certaine liberté d’expression. L’enseignant peut saisir l’occasion de partager plus facilement les idées spontanées des élèves et développer de nouveaux objectifs comme, par exemple, créer de nouvelles règles du jeu…

Il est bien entendu que cette approche ne remplace pas l’acquisition plus structurée des savoirs ou des connaissances. De telles séances avec le jeu Al-Jabr peuvent toutefois contribuer à faciliter l’apprentissage de l’algèbre, elles constituent un levier complémentaire qui suscite chez les élèves des envies de réfléchir, de s’entraider, d’échanger et, en fin de compte, d’apprendre. D’autres pistes sont sûrement à exploiter avec ce jeu, en demandant aux élèves par exemple de créer d’autres familles de 10 cartes ou mieux encore en créant un jeu complet. Ces cartes peuvent être utilisées par la suite pour aborder la résolution d’équations. L’utilisation d’un dé permet aussi d’aborder la notion de probabilité : « Quelles chances j’ai d’obtenir… », « Qu’en serait-il si on disposait de deux dés ? » Les échanges entre et avec les élèves pourront alors être encore plus riches et profitables pour leurs apprentissages.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Olivier Garrigue est professeur de mathématiques au lycée Adam de Craponne à Salon-de-Provence.

Ricardo Lima est physicien, ex-directeur de recherche au CNRS, et fondateur de Dream & Science Factory .

Jorge Rezende est professeur au département de mathématiques de la faculté des sciences de l’Université de Lisbonne.