La magie des azulejos

Qui ne s’est jamais émerveillé devant des azulejos, ces petits carreaux de faïence peints et émaillés qui décorent maisons, gares ou encore églises, et dont l’Espagne et le Portugal foisonnent ? Olivier Garrigue décrit des pistes d’utilisation en classe.

Olivier Garrigue

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

C’est à partir de septembre 2016, par l’intermédiaire de rencontres au sein de l’IREM d’Aix-Marseille, que Jorge Rezende¹, Ricardo Lima² et moi-même avons collaboré afin de travailler sur les azulejos avec des élèves de Sixième (cycle 3) mais aussi avec des élèves de Troisième (cycle 4). Il est important de préciser que le travail que nous présentons aujourd’hui dans cet article n’aurait pu voir le jour sans l’étude mathématique et pédagogique préalable de Jorge Rezende³. Dans notre groupe de travail, il est le premier à s’être intéressé plus particulièrement aux azulejos de l’artiste-peintre Eduardo Nery.

Les premiers pas d’un parcours

Eduardo Nery (1938–2013) est un artiste-peintre portugais qui a, entre autres, travaillé sur la revalorisation des espaces bétonnés urbains. Pour ce faire, il créa des azulejos aux propriétés visuelles et géométriques très intéressantes ; par exemple :

Ainsi, dans un premier temps, nous pouvons évoquer les transformations du plan appliquées à un tel carreau. Par exemple, si nous partons de ce carreau, nous pouvons par exemple lui faire successivement subir des rotations de 90°, 180° et 270°, toujours dans le même sens (ici, sens indirect) :

devient

puis

et enfin

Nous remarquons qu’une fois ces carreaux assemblés, les couleurs se prolongent d’un carreau à l’autre et le tout forme une frise de quatre carreaux avec un axe de symétrie.

À partir de cette simple observation, nous pouvons laisser libre cours à notre imagination et essayer d’envisager tous les assemblages possibles de copies de l’azulejo d’Eduardo Nery. Ci-dessous, pour mieux se rendre compte, nous présentons quelques exemples de ces possibilités visibles à la gare de Contumil (Porto, Portugal) :

Figures 2 et 3. Gare de Contumil (Porto, Portugal).

Crédit photo : Fernando Sousa Lopes.

Dès l’année scolaire 2016-2017, nous avons ainsi choisi de présenter l’azulejo d’Eduardo Nery ainsi que ceux créés par Jorge Rezende⁴ à nos élèves de Sixième dans le cadre d’un « parcours ».

Figure 4. Quatre azulejos de Jorge Rezende.

Ce dispositif repose sur les éléments ci-après que nous allons maintenant détailler.

Une démarche

Au début de l’année, nous démarrons avec les élèves un parcours d’étude sur les azulejos. À raison d’une séance toutes les deux ou trois semaines environ et ceci jusqu’à la fin de l’année, les élèves vont être les acteurs de séances indépendantes de l’enseignement classique que nous leur dispensons au quotidien. Un parcours est ici compris comme un chemin dans un réseau de possibles « sentiers qui bifurquent » (J. L. Borges) dont la concrétisation tient autant aux propositions des élèves qu’au doigté des enseignants attentifs et, qui plus est, va être heureusement propre à chaque élève, et donc différent d’un élève à un autre.

Un artefact

Les azulejos plastifiés, présentés au début comme un trésor caché dans une enveloppe (« habillage pédagogique »), sont étudiés tout au long de l’année. Au rythme des séances, les élèves découvrent différents azulejos : celui d’Eduardo Nery (1966), ceux de Jorge Rezende (2012, …) ou ceux créés par des élèves⁵, etc.

Un carnet de bord

Chaque élève dispose d’un carnet de bord tout au long du projet. Il y écrit tout ce qu’il juge bon pour mieux comprendre la nature de l’objet étudié. Ce carnet lui sert de fil rouge.

L’autonomie

Il est important pour nous de respecter deux points qui nous semblent fondamentaux. Le premier est le principe de la « démarche ouverte », c’est-à-dire que ce sont les élèves qui pilotent le plus possible l’avancée du parcours et les pistes de réflexion. Le deuxième point est le respect du rythme de chaque élève. On prendra garde à une dérive courante de la mise en œuvre d’un tel dispositif, à plus forte raison avec des élèves de Sixième : du fait de leur enthousiasme, ils peuvent rapidement partir dans toutes les directions. C’est ici que le rôle de l’enseignant prend tout son sens. Dans ce type d’enseignement, il est le garant du respect du cadre, c’est-à-dire qu’il peut lui arriver de recadrer le questionnement des élèves par le biais de questions stratégiques.

L’enseignement lié à ce type de dispositif est ainsi principalement axé sur les échanges entre les élèves mais aussi avec les enseignants. Cela n’occulte en aucun cas des phases de travail où l’élève est seul et doit réfléchir par lui-même et des phases où le (ou les) enseignant(s) présent(s) pourra (pourront) intervenir pour synthétiser certaines réflexions par exemple. Nous utilisons ici le terme « enseignants » au pluriel car ce type de dispositif peut conduire à un travail multidisciplinaire.

Pour terminer, nous pouvons ajouter que le travail des élèves sur les azulejos tel que nous l’avons mis en place a comme première conséquence utile de susciter un apprentissage et un renforcement de plusieurs savoirs dans différents domaines (le dénombrement et la géométrie) et dans différentes matières (les arts plastiques et le français notamment). De plus, l’initiative étant le plus possible laissée à l’élève, c’est lui qui doit faire preuve d’esprit critique par rapport à la démarche qu’il a ou qu’il va adopter, c’est ainsi qu’il voit l’intérêt et l’utilité d’élaborer, de construire et de renforcer ses propres connaissances. Cette façon de travailler permet de gérer l’hétérogénéité : chaque élève peut avancer à son rythme et construire ses propres connaissances. Il est aussi bien entendu que chaque élève n’aura pas acquis ni produit les mêmes savoirs et, parfois, sera arrivé au but par son propre chemin. La multiplicité de ces démarches apparaît, à notre avis, comme une des richesses intéressantes de ce parcours. Mais, aucun n’est laissé isolé. Chacun est englobé dans la dynamique de travail de la classe et bénéficie des mêmes points de synthèse élaborés avec le (ou les) professeur(s) ; ce qui est aussi très positif de notre point de vue.

Il va de soi, d’après ce qui vient d’être exposé, que la description des séances de travail qui suit est un des chemins parmi les variantes possibles. Nous espérons néanmoins y donner une idée de la méthode de travail adoptée.

La mise en place du parcours

Lors de la mise en place avec les élèves, nous avons observé trois phases de travail qui jalonnent le parcours. Cette succession se retrouve aussi à chaque séance. Une certaine ritualisation de cette progression a été bénéfique dans le travail des élèves en rendant plus efficaces leurs réflexions.

Phase d’adaptation : pour les élèves et l’enseignant

Les élèves découvrent le cadre de travail et s’adaptent à la situation proposée par l’enseignant. C’est un moment-clef. En ouvrant l’enveloppe, ils découvrent les azulejos et se familiarisent avec cet objet. Nous remarquons le plus souvent que les élèves se posent énormément de questions différentes durant cette phase. Il est bien entendu qu’une fois le parcours mis en place, dès les premières séances, l’enseignant doit montrer une grande part d’adaptabilité aux différentes réactions des élèves. Ainsi, ces derniers vont multiplier les productions, les observations et les questions. On observe des allers et retours multiples de démarches individuelles à des confrontations, voir des compromis ou des synthèses. C’est à partir de cela et des photos qu’il aura prises que l’enseignant peut noter, reformuler et ordonner des questions stratégiques qu’il soumettra à l’ensemble de la classe lors de moments de synthèse et ainsi approfondir l’étude des azulejos.

Figures 5 et 6. Phase d’adaptation : photos de l’enseignant.

Phase d’approfondissement : une manipulation plus réfléchie et des bases pour une bonne investigation

En premier lieu, et en guise de transition, cette phase peut être l’occasion de travailler de manière plus approfondie sur les pavages et la symétrie ainsi que sur les frises et les motifs glissés mais l’objectif principal ici reste d’appuyer la pensée des élèves et de leur permettre de formuler explicitement leurs questions, leurs opinions. Ils continuent de manipuler les azulejos pour mieux expliquer à leurs camarades et/ou au professeur leurs points de vue, leurs questions. Il s’agit ici de leur montrer l’intérêt d’être précis et rigoureux dans leurs investigations.

Figures 7 et 8. Phase d’approfondissement : productions d’un élève.

Phase de synthèse : des éléments de réflexion prépondérants

À la fin de la deuxième phase, il est judicieux de faire une synthèse des réflexions pour lesquelles un consensus a été établi. Jusque-là, lors de nos expérimentations, la question du dénombrement est souvent l’une des questions qui a suscité le plus d’intérêt chez nos élèves, ainsi que la façon dont les azulejos sont conçus pour avoir de telles propriétés. Toutefois, si nous revenons au principe d’un parcours tel que nous l’envisageons, il se peut que les élèves, ou certains parmi eux, ne prennent pas du tout cette orientation et ce sera alors à l’enseignant d’accompagner ces élèves dans de nouvelles voies.

Quelques précisions sur une succession possible de réflexions des élèves

Comme nous l’avons dit précédemment, un travail approfondi sur les transformations du plan peut être effectué à travers la manipulation des azulejos. Soulignons le fait que posséder un appareil photo (ou une tablette) pour garder une trace des productions éphémères des élèves peut se révéler extrêmement utile. En effet, les élèves font et défont des frises et des pavages selon leurs propres réflexions et prendre des photos peut alors permettre à l’enseignant, lors de moments de synthèse, de revenir sur certaines configurations produites.

Le dénombrement des différentes possibilités est aussi l’une des premières questions qui est venue à l’esprit de nos élèves lors des expérimentations que nous avons menées avec eux. Ils rivalisent alors d’imagination pour connaître le nombre exact de possibilités qu’il y a de faire des frises de deux, trois, quatre carreaux et même au-delà. Ils produisent des notations simplifiées des carreaux, ils construisent de leur propre initiative des « arbres des possibles » et dressent des tableaux. Nous avons constaté que cette capacité à inventer et utiliser des notations était un passage très important dans la compréhension et l’explicitation des questions abordées.

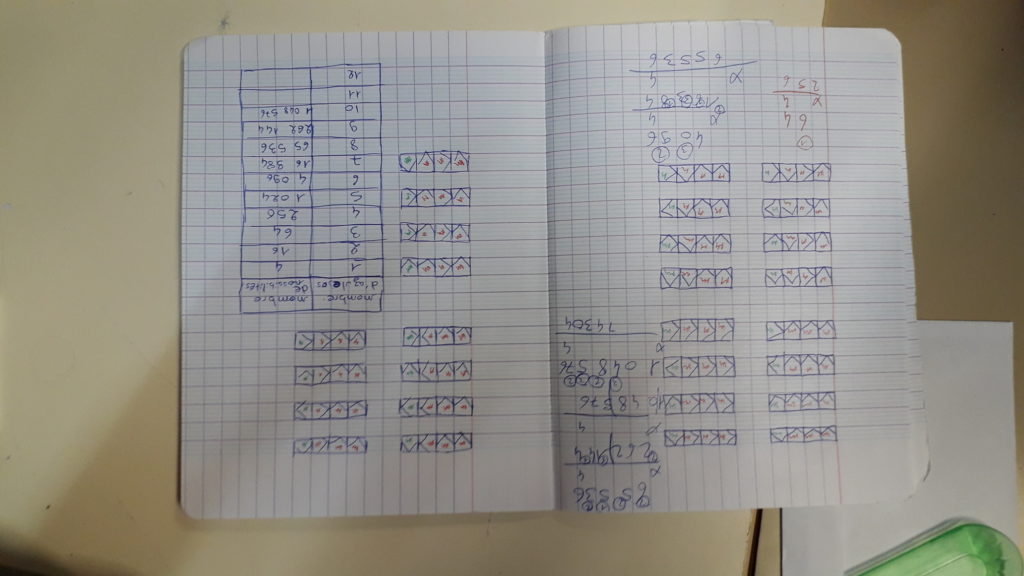
Figures 9 et 10. Dénombrement des possibilités : productions d’un élève.

Lorsque les élèves ont constaté que le nombre de possibilités n’évolue pas de façon proportionnelle par rapport au nombre d’azulejos mis à disposition, le questionnement a tendance à s’arrêter là. Même si, une année, certains élèves sont allés jusqu’à manipuler les puissances de 4 pour exprimer leurs résultats.

L’une des questions qui survient ensuite est la façon de construire son propre azulejo. Nous pouvons dire que les élèves se focalisent d’abord sur les bords de leurs azulejos. En effet les lignes et les couleurs doivent coïncider, mais ils découvrent ensuite qu’établir d’autres règles s’avère nécessaire. Par exemple, l’une des autres règles qui fait rapidement consensus lorsque les élèves constatent que l’un d’entre eux s’applique à tracer le deuxième en décalquant est que les carreaux doivent être identiques, « superposables ». Pour ce qui est d’autres règles, elles s’ajoutent au fur et à mesure des différentes tentatives et à l’issue de moments de synthèse effectués en classe entière. À noter que certains élèves sont même allés jusqu’à établir une fiche d’aide et d’auto-évaluation pour mieux encadrer le travail de confection de leurs azulejos (voir annexe).

Voici ci-dessous quelques exemples de productions d’élèves :

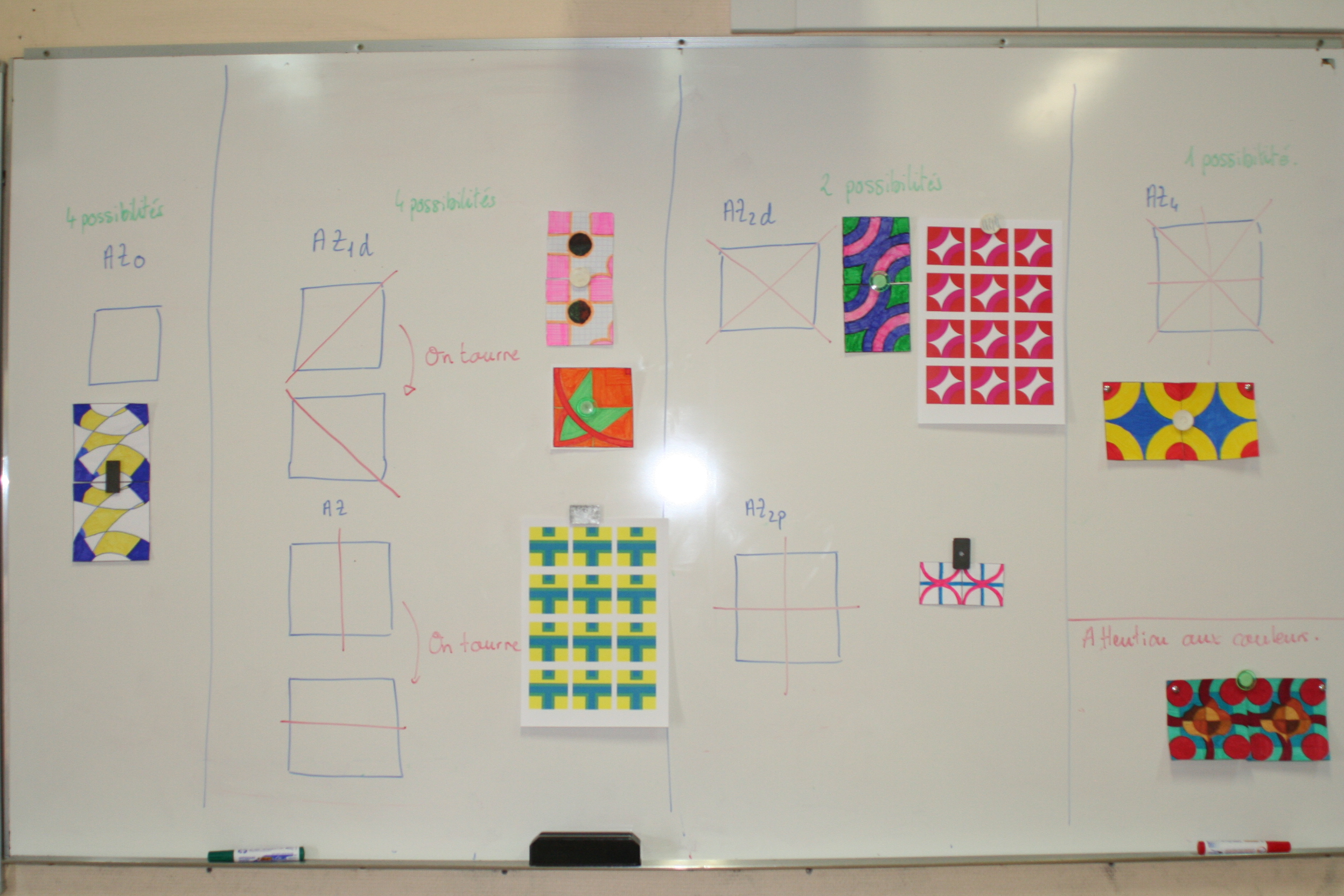
Pour finir, le travail des élèves en fin d’année a souvent abouti à des exposés visant à retracer l’ensemble de leurs parcours sur les azulejos tout en y incluant des éléments historiques et architecturaux trouvés à l’occasion de recherches au CDI et à la médiathèque de la commune. Un travail en arts plastiques sur les azulejos a aussi donné lieu à une réflexion plus poussée sur l’utilisation des couleurs et des matériaux pour une confection plus élaborée d’azulejos. Une année, en dernière période, après avoir créé plusieurs azulejos, certains élèves ont compris que le nombre d’axes de symétrie pouvait avoir une influence sur le nombre de possibilités de créer des frises de deux, trois, quatre carreaux, … Ces élèves ont ainsi établi une classification des azulejos en fonction du nombre d’axes de symétrie qui les composent.

Pour aller plus loin…

Nous avons pu mener des expérimentations ponctuelles avec des élèves de Troisième. Ceci afin d’avoir une vision plus large de l’utilisation qui peut être faite des azulejos dans l’enseignement des mathématiques.

Plus particulièrement, lors de l’année scolaire 2016-2017, lors d’un travail de groupe, des élèves de Troisième ont pu manipuler les azulejos plastifiés d’Eduardo Nery et de Jorge Rezende, il leur a ainsi été proposé sur deux séances la question suivante :

Question
Quel type de programme informatique simple pourrait-on proposer à des utilisateurs (des élèves de Sixième par exemple) ou à des « spectateurs » (des adultes venant apprécier le travail des élèves de Sixième et de Troisième par exemple) afin de vivre et de partager une partie de l’expérience vécue par les élèves de Sixième lorsqu’ils ont étudié les azulejos cette année ?

À noter que plusieurs idées ont été échangées par les élèves du groupe. Ci-dessous trois de leurs projets qui ont été retenus :

Projet 1 : « Créer un programme où l’utilisateur peut « cliquer » sur un des azulejos du pavage déjà en place pour le tourner autant qu’il veut ; si c’est une tablette ce sera encore mieux ».
Projet 2 : « Créer un programme où l’ordinateur construit au fur et à mesure le pavage en demandant à chaque fois à l’utilisateur quelle position il doit donner aux azulejos ».
Projet 3 : « Créer un programme qui, une fois lancé, agit de façon autonome pendant une heure en exposant aux spectateurs un pavage qui évolue toutes les secondes de façon aléatoire ».

Ces programmes⁶ ont été exécutés tour à tour sur tablette⁷ et en vidéo-projection aux participants de l’atelier afin de mieux apprécier le travail des élèves.

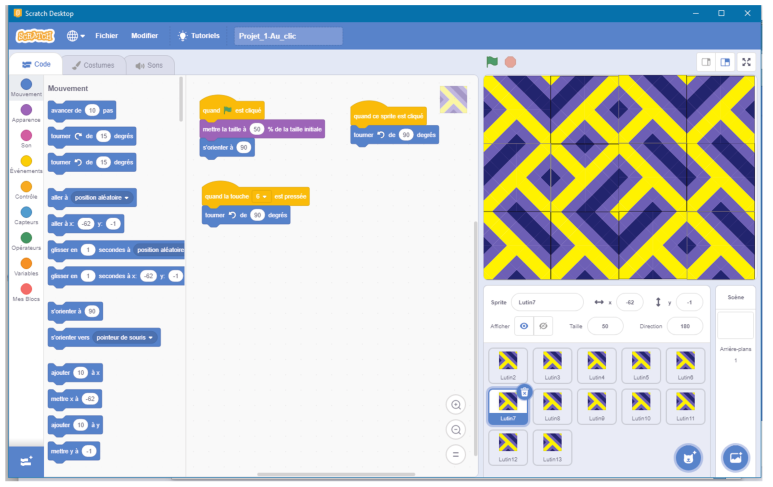
À noter que les groupes menant les différents projets ont notamment échangé sur la meilleure façon d’insérer en tant que « lutin » l’azulejo d’Eduardo Nery et sur la façon dont ils allaient montrer et expliquer leurs différents programmes aux élèves de Sixième. Des rencontres avaient pu être menées en fin d’année entre les élèves de Sixième et de Troisième.

Conclusion

Nous ne pensons évidemment pas que cette approche remplace l’acquisition plus structurée des savoirs ou des connaissances. Mais elle constitue un levier complémentaire qui suscite chez les élèves des envies de réfléchir et d’apprendre.

Il faut aussi garder à l’esprit que d’autres usages des azulejos sont possibles. Selon le principe du parcours tel que nous l’avons défini plus haut, les élèves peuvent prendre d’autres directions lors de l’étude des azulejos. Les démarches que nous avons donc exposées ici sont celles qui sont revenues lors de nos trois années d’expérimentation. Nous sommes aussi conscients que des enseignants pourront utiliser les azulejos d’une toute autre manière. Par exemple, des élèves du primaire (CE1 et CE2) ont utilisé les azulejos dans un jeu de « figures téléphonées » : décrire l’orientation d’un carreau caché jusqu’à ce que cette orientation soit devinée par un camarade nécessite de travailler le langage.

Enfin, l’étude des azulejos créés par Eduardo Nery puis Jorge Rezende peut nous amener à travailler différentes notions abordées en arts plastiques, en mathématiques, en histoire et dans bien d’autres disciplines encore. Les élèves ne s’y trompent pas et suggèrent souvent des pistes de réflexions pouvant faire appel à plusieurs de ces domaines en même temps ou successivement. Ainsi, les azulejos présentent une occasion toute naturelle d’envisager un travail multidisciplinaire.

Annexe

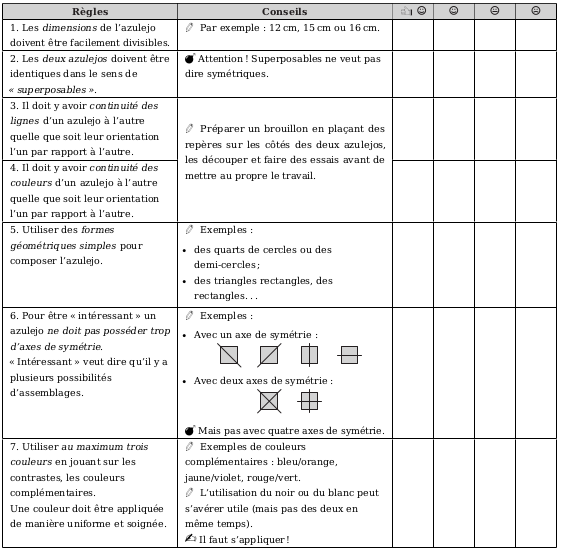
Fiche d’aide pour construire un azulejo. Synthèse classe année 2017/2018 à partir des propositions des élèves.

Conception de deux azulejos identiques : rappel des règles de construction.

Cette fiche sert à :

se souvenir des règles et des observations faites en classes sur la conception de deux azulejos identiques ;
utiliser les conseils pour mieux accomplir le travail demandé ;
auto-évaluer son travail en se servant des quatre colonnes de droite.