Le château de cartes

Faire chercher les élèves ? Voici un des objectifs de tous les collègues ! Claire Lommé propose dans cet article, illustré par Olivier Longuet, une activité de recherche en Sixième à partir d’un problème en vidéo qui vous donnera très certainement envie d’essayer.

Claire Lommé & Olivier Longuet

© APMEP Mars 2022

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Tous les ans, je propose à mes élèves de Sixième le problème en vidéo du château de cartes des Dudu . D’habitude, je l’aborde plus tôt dans l’année. Mais cette année, avec ma nouvelle programmation, il a trouvé sa place au mois de décembre. Cette temporalité différente fait que nous avions déjà traité cinq ou six « gros » problèmes: des problèmes en dessin, en vidéo, en photo, en anglais, mais tous robustes, qui ont résisté et demandé d’unir nos forces. Les élèves avaient aussi déjà participé à des concours ou des rallyes (comme le Rallye Maths’n Caux , le concours Castor informatique , le rallye IREM ou la course aux nombres¹).

La situation et son explicitation

Dans mes deux classes de Sixième, j’ai travaillé ce problème en demi-classe. D’abord, j’ai diffusé la vidéo, une à deux fois selon les groupes: deux demi-classes ont capté la problématique et toutes les informations du premier coup, les deux autres non. J’ai demandé aux élèves de reformuler le problème. Par exemple, un groupe s’est mis d’accord sur « On va chercher combien il faut de paquets de 32 cartes pour faire un château de cartes de 2,50 mètres de haut. Et on répondra à Julien qui se demande si 10 paquets ça suffit ». Je leur ai projeté un diaporama² qui explique comment on construit un château de cartes, avec une diapositive « coup de pouce » qui parfois est utile pour relancer les élèves désemparés. Mais pas cette année

Représentations/modélisation, phase 1

Sur quatre niveaux, nous dénombrons les cartes nécessaires. Cette année, plusieurs élèves ont vu tout de suite qu’« on ajoute trois cartes de plus à chaque fois qu’on en ajoute, par rapport à la fois d’avant ». Ça m’a bluffée, comme ça, pouf, d’emblée. Du coup, j’ai dégoupillé la version 2 du diaporama, celle qui fait apparaître le nombre de cartes ajoutées à chaque niveau supplémentaire, du niveau 1 au niveau 4.

Nous simplifions la problématique ainsi:

1. 320 cartes suffiront-elles ? Ou en faudra-t-il 600 ? Ou 900 ?

2. Combien faut-il d’étages ?

3. Combien mesure la hauteur d’un étage ?

4. Combien faut-il de cartes pour réaliser 31 étages ?

L’étape « Combien mesure la hauteur d’un étage ? », qui permet de déterminer combien on vise d’étages (31 cette année, mais cela dépend des choix des élèves), a été particulièrement intéressante car beaucoup d’élèves, spontanément, mesurent une carte. D’autres interviennent toujours: « Non, ça ne va pas, les cartes sont penchées, la hauteur d’un étage va être plus petite que la taille d’une carte ». Ce qui est également intéressant, c’est qu’il faut décider: les élèves aimeraient qu’il y ait une hauteur standard de niveau de château de cartes. Mais ils doivent décider. Cette année, comme tous les essais donnaient entre 7,5 cm et 8,5 cm, les élèves ont choisi 8 cm, en justifiant que c’était plus pratique pour diviser. Mais diviser quoi, au fait? Il a fallu se mettre d’accord:

« Il faut une division parce qu’on veut savoir un nombre de paquets dans un ensemble de trucs.
— On divise 250 par 320 ?
— Non, 320 c’est les cartes. Tu peux pas diviser des centimètres par des cartes, enfin pas comme ça là.
— Et 320 on n’est même pas sûr, peut-être c’est moins ou plus.
— Il faut chercher les étages, donc combien de fois il y a 8 cm dans les 2,50 m.
— On va après la virgule ou pas ?
— Ben non, on va pas avoir des nombres de cartes à virgule. »

Très bien, bonne idée, on y va. Les élèves choisissent une unité, convertissent, posent la division, que nous avons longuement justifiée (j’ai aussi pour objectif de travailler le sens des opérations et la réversibilité multiplication/division). Dans tous les cas, la division donne un reste de 2. Et je passe beaucoup de temps sur l’interprétation de ce 2; j’entends:

« Il reste 2 cartes
— Il reste 2 étages
— Il faut 2 étages
— Il reste 2 paquets
— Il reste 2 cm. »

Et comme je veux que les élèves comprennent par eux-mêmes, il faut des débats et du temps pour que chacun conclue qu’avec 31 étages de 8 cm de haut, on atteint 248 cm . Il reste donc 2 cm entre le sommet du château et le plafond. Certains élèves, pour s’en convaincre, ont dû poser la multiplication \(31\times 8\) — comme quoi le sens de la division n’est pas encore assimilé pour tous — il se trouve que cela va dans le sens de ce que je veux travailler: c’est très bien.

Mais ensuite, question supplémentaire: est-ce embêtant qu’il reste 2 cm ? Là, j’ai eu droit à un « Pffffff, noooooon ! » qui sentait le « On va pas s’embêter, madame, allez ». Et des élèves ont trouvé un compromis acceptable pour les puristes que cela gênait: « On va resserrer un peu les cartes des piliers quand on arrivera vers le haut. On va gagner des millimètres et comme ça on va réussir à faire 2,50 m ». Bon, tout le monde est d’accord.

Intermède 1

« Madame, on n’a pas tenu compte d’un truc, mais il le faut: ça va prendre de la place, et sur la table bah à mon avis ça tient pas. »

C’est la première année qu’un élève me fait cette remarque. Et c’est très pertinent. Du coup, nous nous sommes donnés une tâche secondaire : calculer la longueur au sol du château. Et de là l’idée est née: on va construire le château si ça tient dans la classe. On va tous ramener des paquets de cartes, et on va le construire en collant. Et on prendra une photo et on l’enverra aux Dudu³.

« Hein oui madame on peut hein dites ?
— Rho oui, c’est rigolo. Mais sur le temps du midi, alors, ok ? Et avant tout il faut résoudre le problème: je dois savoir de combien de paquets de cartes nous aurons besoin, et la taille du château.
— Ouééééééééééé ! »

Forcément, ça motive, la mise en projet.

Intermède 2

« Mais au fait, à vue de nez, comme ça pouf à la louche, vous diriez combien de cartes ? »

Parce qu’estimer, c’est important, aussi.

Représentations/modélisation, phase 2

Chacun s’est mis à chercher, en groupes évolutifs (des groupes se forment mais les élèves ont le droit d’aller voir ailleurs, de s’incruster, d’échanger leurs places…). Voilà quelque chose que mes élèves auront appris: aller chercher l’avis d’un autre groupe ou une inspiration chez ceux qui ont l’air de «trouver des trucs». Plus tôt dans l’année, cela finissait parfois un peu en pugilat si je n’intervenais pas à temps, mais on a progressé. Aujourd’hui, ça roule bien.

Plusieurs questions se sont posées:

• est-ce qu’on peut réfléchir sur un plus petit château et après multiplier ? Par exemple, on part sur nos 4 niveaux et on multiplie par 4 et on enlève un étage ;

• est-ce que chaque étage comporte le même nombre de cartes ?

• est-ce que chaque étage comporte la moitié des cartes de l’étage précédent ?

Autrement dit, nous avons parlé proportionnalité. C’était très enrichissant pour moi, car comme nous étions en dehors d’un abord explicite de la proportionnalité, nous avons pu creuser et le mot « proportionnalité » n’est apparu que très tardivement, nous laissant le temps de réfléchir sans chercher à se ramener à une représentation étroite de la question.

Résolution

Nous n’avions qu’une heure, quand même… Et pourtant, nous avons résolu le problème. Nous avons eu recours au tableur pour terminer et vérifier les calculs. Les élèves avaient bien retenu l’utilisation de formules et ont été capables de me dire quoi écrire dans mon tableur.

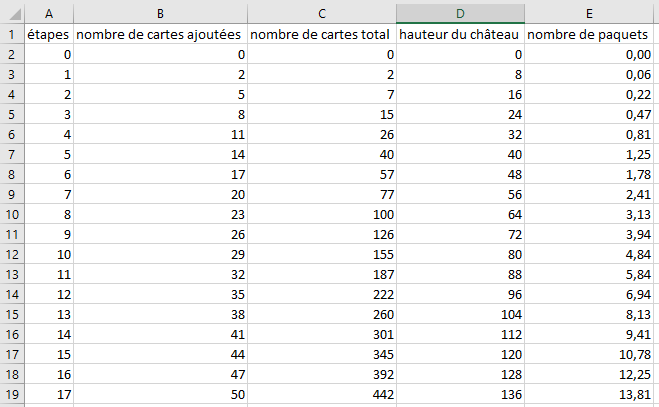
Mais surtout, ils avaient trouvé, par plusieurs méthodes différentes. En voici quelques-unes.

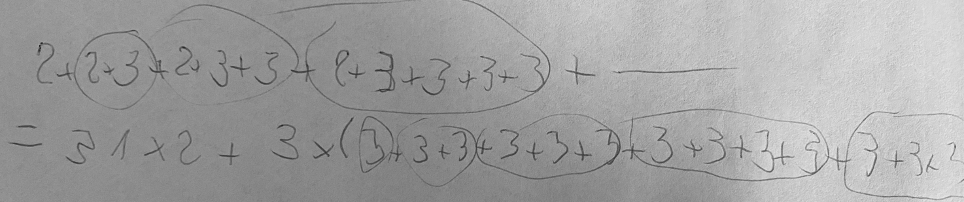
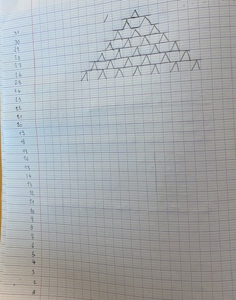
Conclusion

Franchement, je vous conseille vraiment ce problème. On aborde plein de thématiques: la résolution de problème, l’argumentation… mais aussi le sens des opérations, les distances ou les conversions. Et puis la question est concrète, tout en n’étant pas facile à réaliser sur le plan pratique. Parfait pour modéliser de façon naturelle.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Claire Lommé est enseignante de mathématiques et formatrice académique. Elle enseigne au collège Jean de la Varende à Mont-Saint-Aignan (Haute-Normandie) et intervient dans la formation, continue et initiale. Elle est aussi l’auteure du blog PIERRE CARRÉE

Olivier Longuet enseigne les mathématiques au lycée Alain Chartier de Bayeux. Il est membre de l’équipe de rédaction d’ Au fil des maths et notamment l’auteur de certaines des illustrations. N’hésitez pas à parcourir son blog