Le Rallye Mathématique Transalpin

Que ce soit en primaire, au collège ou au lycée, ce n’est pas toujours simple de trouver de « bons » problèmes pour mettre les élèves en situation de recherche. Christine Le Moal présente ici le Rallye Mathématique Transalpin et ses problèmes de recherche ainsi que tous les outils qui ont été développés sur lesquels il est aisé de s’appuyer. Une ressource très riche du CE2 à la classe de Seconde. N’hésitez pas à vous lancer

Christine Le Moal

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Présentation

En Franche-Comté, environ 400 classes de Sixième, Cinquième et Quatrième participent chaque année au Rallye Mathématique Transalpin (RMT). Ce rallye est une confrontation entre classes, chaque classe doit résoudre sept problèmes en 50 minutes et fournir, pour chaque problème, une réponse argumentée unique. Ces problèmes sont systématiquement des petites énigmes contextualisées où se cachent un peu de mathématiques : logique, combinatoire, arithmétique, calculs numériques et proportionnalité, géométrie, suites, fonctions et probabilités pour les deux catégories les plus élevées. L’attribution des points dépend de la rigueur des démarches et de la clarté des explications fournies.

Le rallye s’effectue en trois étapes (éventuellement quatre) : en décembre, une épreuve d’entraînement à l’issue de laquelle la décision est prise d’inscrire ou non la classe, en février et en avril deux épreuves du type décrit ci-dessus et, pour les dix meilleures classes (par niveau) à l’issue de ces deux épreuves, une épreuve finale en mai, toujours du même type.

Le RMT est un rallye international. Plus de vingt sections, soit environ 4000 classes, l’organisent, essentiellement en Italie, mais aussi en Belgique, en Suisse et au Luxembourg. Il s’adresse à des élèves depuis le CE2 (catégorie 3) jusqu’à la Seconde (catégorie 10)¹.

Tout au long de l’année, dans chaque pays participant, les différentes sections fabriquent, choisissent, adaptent, enrichissent le stock des problèmes. Lors de journées d’études internationales, les animateurs des différents pays participants déterminent les exploitations didactiques des problèmes du RMT et produisent des analyses a priori (pour aider l’enseignant à anticiper le travail des élèves) et a posteriori (pour rendre compte de réussites et d’échecs d’élèves par catégorie). Ces travaux sont accessibles sur le site de l’association ARMT [1] et les problèmes et leurs analyses sont regroupés dans une banque de problèmes² [2].

En quoi proposer ce type de problèmes aux élèves contribue-t-il à leurs apprentissages mathématiques?

Le groupe de l’IREM de Besançon qui gère l’organisation du RMT en Franche-Comté travaille également à promouvoir auprès des enseignants la recherche de problèmes dans leur pratique régulière de la classe. En effet, beaucoup de professeurs inscrivent leurs classes pour participer au concours, mais n’utilisent pas les problèmes à d’autres moments que lors des trois épreuves annuelles. Or l’apprentissage de la résolution de problèmes ne se fait pas en quelques séances ponctuelles. Il faut mettre plus souvent les élèves en situation pour leur permettre de construire des méthodes de recherche et de mobiliser des connaissances anciennes. Pour illustrer ce propos, appuyons-nous sur quelques travaux de recherche.

Par exemple, Catherine Houdement [3], chercheuse en didactique des mathématiques à Rouen, définit plusieurs sortes de problèmes arithmétiques :

des problèmes qu’elle a appelés «basiques»: « il s’agit des problèmes qui constituent des éléments “simples” du raisonnement au sens de la chimie de Mendeleev » (problèmes à une étape, ou problèmes à deux données numériques où il faut trouver la troisième, ou proportionnalité simple, ou problèmes sans trop d’informations et où celles-ci sont connectées) ;
elle distingue ensuite deux sortes de problèmes qui ne seraient pas basiques :
- d’abord « des “problèmes complexes” qui sont des agrégats de “problèmes basiques” » (il faut connecter les informations qui sont dans le texte ou il faut qualifier la réponse),
- et ensuite « des “problèmes atypiques” définis justement par leur caractère non routinier, le fait qu’on suppose que les élèves ne disposent pas de stratégies connues pour les résoudre, qu’ils doivent en inventer de toutes pièces, en s’appuyant sur leurs connaissances passées, notamment leur mémoire des problèmes ».

Le psychologue cognitiviste Jean Julo souligne quant à lui l’importance de la représentation (mentale) dans le processus de résolution de problèmes. Il ne suffit pas de comprendre l’énoncé au sens sémantique du terme, il faut aussi comprendre les relations complexes entre le but donné et les conditions de réalisation de ce but. D’après lui, nous aurions chacun une mémoire des problèmes qui nous permettrait de reconnaître et de traiter des problèmes « ressemblants »³ de façon presque « automatique ». Et nous enrichissons cette mémoire grâce à la résolution réussie de problèmes que nous menons à terme [4] et [5].

En conclusion, pour retirer les bénéfices de la recherche de problèmes, il faut s’engager dans une pratique régulière avec le souci de faire réussir les élèves par eux-mêmes, accepter qu’ils essaient, échouent, recommencent, en leur donnant des coups de pouce si besoin mais sans « tuer » le problème: «trop expliquer, c’est empêcher de comprendre» selon les recommandations du GFEN⁴.

Contribution du RMT à la résolution de problèmes

Pour s’engager dans une telle démarche, le RMT est une source très riche. Il propose des problèmes complexes ou atypiques. Confronter les élèves à la résolution de tels problèmes favorise la construction et l’utilisation de connaissances et développe leur inventivité stratégique. Cela permet aussi à l’enseignant d’évaluer (formativement) chez les élèves la connaissance (voire la méconnaissance) de notions déjà enseignées. De plus, le travail collaboratif des élèves pendant la recherche participe positivement à la construction des savoirs; il stimule leur intérêt pour la résolution de problèmes de mathématiques.

Pour anticiper les difficultés et préparer les coups de pouce, on trouvera dans la banque de problèmes des analyses a priori (analyse générale de la tâche, démarches attendues des élèves, obstacles prévisibles) et des analyses a posteriori s’appuyant sur des productions d’élèves. Ces analyses permettent de repérer les connaissances minimales nécessaires à la résolution du problème et si besoin d’envisager des problèmes basiques à construire au préalable. Elles permettent également d’anticiper certaines stratégies, certaines erreurs, de repérer les déficits de connaissances des élèves et d’envisager des variantes pour simplifier ou au contraire complexifier le problème en fonction du niveau scolaire des élèves [6].

Un exemple

En cette année 2019, le problème «La tarte aux fruits» faisait partie des problèmes de l’épreuve d’entraînement des classes de Sixième en Franche-Comté:

LA TARTE AUX FRUITS (Cat. 4, 5, 6, 7)⁵

Pauline a invité ses amis pour fêter son anniversaire.
Son papa a confectionné une excellente tarte aux fruits et, pour contenter tout le monde, il l’a découpée en parts de mêmes dimensions et avec le même nombre de fruits sur chaque part de tarte.
La fête est finie, Pauline constate qu’il reste une seule part de tarte. Sur cette part elle compte 17 fruits et elle s’exclame: «Tu as vraiment utilisé beaucoup de fruits pour faire la tarte, papa! »

Ce dessin représente la part de tarte posée sur la table, vue du dessus:

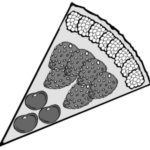
Combien de fruits le papa de Pauline a-t-il utilisés en tout pour décorer la tarte entière?
Montrez comment vous avez trouvé votre réponse.

Le groupe qui l’a cherché dans ma classe de 6^e y a passé très peu de temps et a répondu :
« \(8 \times 17 = 136\) donc il y a \(136\) fruits. » Cette réponse est fausse car il faut \(9\) parts pour reconstituer la tarte entière.

Quand j’ai fait le bilan de l’épreuve d’entraînement, j’ai indiqué rapidement qu’ils n’avaient pas trouvé la bonne réponse à ce problème mais sans le corriger, car je voulais le réutiliser plus tard dans l’année au moment du travail sur les angles.
J’ai alors consulté l’analyse a priori de ce problème disponible dans la banque :

ANALYSE A PRIORI

Tâche mathématique
Déterminer le nombre de secteurs circulaires superposables en lesquels un disque a été partagé, à partir du dessin d’un des secteurs (dont l’angle mesure 40°), pour trouver le nombre total d’objets disposés sur le disque, sachant que sur chaque secteur il y en a \(17\).
…/…

Analyse de la tâche

Se représenter la tarte et comprendre qu’elle a été partagée en parts égales, de la même forme, de mêmes dimensions, avec le même nombre de fruits. Comprendre que les parts étant l’une à côté de l’autre, deux parts voisines ont un «côté» en commun.
Comprendre que pour trouver le nombre total de fruits utilisés, il faut reconstituer la tarte entière, de manière à connaître le nombre de parts en lesquelles la tarte a été découpée.
Pour reconstruire la tarte, on peut procéder de différentes manières.
- Découper une part égale à celle qui est dessinée (à partir d’une autre copie de l’énoncé ou en utilisant une feuille de papier calque), la poser à côté de la part donnée, en marquer le contour et continuer de même à reporter cette part sur le dessin de proche en proche, jusqu’à compléter toute la tarte. Compter le nombre des parts ainsi dessinées (9) (stratégie 1)
- Ou bien, à partir du dessin d’une part, dessiner une autre part égale en pliant la feuille le long d’un côté de la première part et en traçant l’autre côté par transparence et continuer ainsi de suite (stratégie 2)
- Ou bien, tracer un cercle ayant pour centre la «pointe» de la part de tarte et pour rayon le «côté» de cette part, reporter l’arc ou la corde ou l’angle au centre, compter le nombre d’arcs, de cordes ou de secteurs angulaires (stratégie 3)
- Ou bien, mesurer au rapporteur l’angle de la part de tarte (40°) et déterminer le nombre de parts en calculant \(360 \div 40 = 9\) (stratégie 4)
- Il est aussi possible de dessiner les parts de tarte « à l’œil », mais cette procédure a peu de chances de donner le nombre exact de parts (stratégie 5)
Multiplier le nombre de fruits d’une part par le nombre de parts: \(17 \times 9 = 153\).

L’analyse de la tâche m’a permis de constater que les procédures possibles étaient nombreuses (cinq différentes citées) et qu’elles correspondaient bien aux attendus du programme :

Angles

Identifier des angles dans une figure géométrique.

Comparer des angles, en ayant ou non recours à leur mesure (par superposition, avec un calque).

Reproduire un angle donné en utilisant un gabarit.

…

Utiliser le rapporteur pour :

Déterminer la mesure en degrés d’un angle

…

Le moment venu, j’ai donc proposé ce problème à toute la classe. Nous n’avions pas encore évoqué la notion d’angle, c’était donc pour moi l’occasion de constater quelles étaient leurs connaissances sur cette notion.

Comme d’habitude lorsque nous travaillons sur la recherche de problèmes, les élèves s’installent en groupe. Je leur explique qu’ils ont droit à tous les outils à leur disposition (cahier de leçons, livre, dictionnaire, calculatrice, matériel de géométrie) et qu’ils peuvent découper, dessiner et écrire sur l’énoncé. Je leur fournis aussi des feuilles de brouillon, du papier calque et d’autres énoncés.

J’ai pu alors observer différentes stratégies:

Un groupe a évalué « à l’œil » \(8\) parts (stratégie 5), mais quand je lui ai demandé de vérifier sa réponse, il s’est alors impliqué dans une reproduction des parts pour obtenir la tarte entière et s’est rendu compte de son erreur.
Stratégie 3 avec report de l’arc :
La plupart des groupes ont utilisé la stratégie 1, avec dessin ou non des fruits.

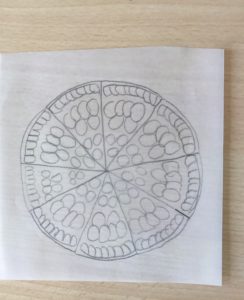
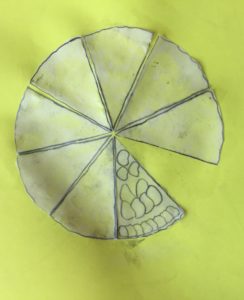
Mais ils se sont rendu compte qu’avec la précision de leurs découpages et collages, la dernière part était souvent trop petite.

Pourtant aucun élève n’a eu l’idée de mesurer l’angle au sommet de la part de tarte (stratégie 4); la notion abstraite d’angle (une grandeur) n’était pas une connaissance disponible pour eux. Nous l’avons donc travaillée par la suite, ce qui a permis de valider la réponse du problème : \(9\) parts et \(153\) fruits.

Ce problème utilisé comme découverte d’une notion était très intéressant car atypique. De premier abord, il avait plutôt l’air d’un problème de proportionnalité, et il s’est révélé être un très bon support pour introduire la nécessité de comparer des angles, de trouver des relations entre eux.

Autre exemple: recherche dans la banque sans idée préalable du problème

Je souhaite travailler sur la visualisation dans l’espace. Je cherche dans la banque de problèmes en utilisant le critère «familles», je choisis 3D/VS/changer de point de vue, et parmi les problèmes proposés, en fonction de la catégorie et du résumé des situations, je choisis « Lettres sur le cube, ral.18.II.16 ».

16. LETTRES SUR LE CUBE (Cat. 7, 8, 9, 10)

Roberto a construit un cube.
Il a écrit une lettre sur chaque face.
Il a ensuite photographié son cube dans plusieurs positions.
Voici trois de ces photos:

Carlo trouve que le cube de son ami Roberto est très intéressant et décide de construire, pour lui-même, un cube parfaitement identique.
Il a préparé un patron de son cube, avec les six faces qu’il va plier et coller avec du papier adhésif transparent.

Il a déjà dessiné le A et un I sur deux des faces.

Dessinez les lettres des quatre autres faces du cube de Carlo pour qu’elles se retrouvent dans les mêmes positions que sur le cube de Roberto.

Y a-t-il plusieurs possibilités de placer les lettres sur ces quatre faces?
Si oui, faites un dessin pour chaque possibilité.

La lecture des résultats et des procédures, obstacles et erreurs relevés m’apprend que ce problème est plutôt bien réussi, que la difficulté se trouve dans le placement des lettres F et I et dans la recherche de plusieurs solutions.

Mais surtout, l’exploitation didactique me donne des pistes pour aider les élèves qui auront des difficultés :

construire un développement du cube, y noter les lettres et vérifier;
décrire oralement le mouvement qui permet de passer du cube dans sa première position (image de gauche) à sa troisième position (image de droite) et noter les positions de la lettre H dans ce mouvement;
confronter les observations des différents élèves pour déterminer celles qui sont les plus efficaces dans la procédure d’identification des faces.

Ce problème existe également avec des figures géométriques à la place des lettres pour les catégories 3, 4 et 5 (c’est-à-dire CE2, CM1 et CM2): « Le cube décoré, ral.3.F.04 ». Je peux donc anticiper les difficultés qui pourraient apparaître pendant la séance, proposer à certains groupes, peut-être, le problème des catégories inférieures, apporter des cubes, du papier pour qu’ils puissent découper et construire.

Conclusion

Les problèmes du RMT et leurs fiches d’exploitation que l’on trouve dans la banque de problèmes sont donc une source très riche pour les enseignants, dès le cycle 3. Proposer de résoudre en classe un problème en ayant au préalable des éléments sur les obstacles que les élèves peuvent rencontrer et des pistes pour les aider est rassurant et permet de gagner beaucoup de temps. Alors n’hésitez pas à vous lancer! Vous constaterez que vos élèves y prendront vite goût et qu’ils seront très inventifs dans leurs stratégies.

Références

[1] ARMT. Site de l’association ARMT.. 2019↩
[2] ARMT. Banque de problèmes de l’ARMT. . 2019.↩
[3] Catherine Houdement. « Résolution de problèmes arithmétiques à l’école ». In : Grand N n°100 (mai 2017). ,pp. 59-78.↩
[4] J. Julo. Représentation des problèmes et réussite en mathématiques. Rennes : Presses Universitaires de Rennes,1995.↩
[5] J. Julo. « Aider à résoudre des problèmes. Pourquoi ? Comment ? Quand ? » In : Actes du XXVII^e colloque inter-IREM des formateurs et professeurs de mathématiques chargés de la formation des maîtres. Grenoble : Université Joseph Fourier, 2001.↩
[6] Francine Athias et al. « Comprendre un énoncé, expliquer à l’écrit une procédure, expliciter oralement une procédure ». In : La Gazette de Transalpie n°8 (octobre 2018)., pp. 162-170.↩
[7] B. Anselmo et M. Henry. « Les problèmes du Rallye Mathématique Transalpin, une ressource pour la formation des enseignants ». In : La Gazette de Transalpine n° 5 (janvier 2017)., pp. 39-52.
[8] Graziella Telatin. « Utilisation en classe des problèmes du RMT ». In : La Gazette de Transalpine n° 3 (octobre 2013)., pp. 131-138