Loyd vs Dudeney
Comment allier mathématiques, anglais et oral ? Emmanuelle Pernot et Fatih Pinar partagent dans cet article une séquence fascinante réalisée entre deux classes de Terminale dans le cadre d’une section européenne.
Emmanuelle Pernot & Fatih Pinar
© APMEP Décembre 2020
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Introduction
Enseignants de mathématiques en section européenne anglais en terminale, nous avons eu envie de monter un projet pour nos deux groupes permettant aux élèves de mettre en œuvre leurs compétences mathématiques et linguistiques. En effet, l’axe prioritaire de l’enseignement en SELO (Section Européenne ou de Langue Orientale) est l’acquisition d’une aisance à l’oral en anglais sur un sujet mathématique. Néanmoins, trouver des sujets qui combinent adroitement et efficacement un sujet mathématique et des compétences linguistiques n’est pas toujours si aisé. Passionnés d’énigmes et de puzzles, nous avons décidé de nous intéresser à l’histoire de l’Américain Sam Loyd (1841-1911) et de l’Anglais Henry Dudeney (1857-1930). Ces deux hommes contemporains ont publié de très nombreux travaux : puzzles, énigmes, tangrams, en abordant presque tous les champs mathématiques (géométrie, algèbre, arithmétique, …). Loyd et Dudeney étaient au début de leur carrière amis et collaborateurs mais par la suite se sont avérés devenir «rivaux». En effet, d’après Dudeney, une fois que Loyd est reparti dans son Amérique natale, il se serait largement inspiré de ses travaux et les aurait même plagiés.
Travail préparatoire
Une fois l’idée thématique trouvée, il nous a fallu élaborer une trame pour ce projet. Assez rapidement, il nous a paru pertinent de recréer la «rivalité» entre Loyd et Dudeney à travers nos classes. Une classe a donc travaillé sur Sam Loyd et l’autre sur Henry Dudeney. Nous avons souhaité imaginer un scénario dynamique alliant des temps de recherche et de réflexion et des temps d’interaction et d’échange. Chance pour nous, nos deux heures de cours par semaine avec ces terminales en section européenne étaient alignées (c’est-à-dire que nous avions nos heures au même moment dans la semaine). Nous avons donc pu envisager un planning mêlant des heures de travail en classe et des heures de regroupement des deux classes. En parallèle, nous avons recherché quelques informations sur Loyd et Dudeney, mais surtout sur leurs travaux. Un document provenant de l’académie de Nancy , classant les riddles («énigmes» en français) de Loyd par thème, nous a été d’une grande utilité, mettant en lien les publications de Loyd avec celles de Dudeney. Nous avons alors pu sélectionner plus aisément les énigmes sur lesquelles nous souhaitions faire travailler nos élèves. Mais le choix n’a pas été simple étant donné la richesse et la multitude des travaux de ces deux amateurs d’énigmes. La séquence entière a été calibrée sur sept semaines, avec un découpage en quatre étapes.
Première étape : immersion dans le projet
Pour lancer le projet, nous avons décidé de ne rien dévoiler de la trame prévue aux élèves et les deux classes ne savaient pas qu’elles allaient travailler ensemble dans les semaines à venir. La classe d’Emmanuelle Pernot aurait à étudier la vie de Henri Dudeney et celle de Fatih Pinar celle de Sam Loyd. Chaque classe a été divisée en sept groupes (numérotés de 1 à 7) de trois ou quatre élèves. Nous avons demandé à chaque groupe d’élèves d’effectuer quelques recherches sur l’internet au cours d’une première séance sur le mathématicien qui leur était attribué, puis de préparer une petite présentation orale au cours de la deuxième séance. Les élèves ont rapidement été attirés par les énigmes de chaque mathématicien et ont préparé des présentations, aucun support particulier n’ayant été précisé. Pour la troisième séance, nous avons regroupé les deux classes et les groupes ayant le même numéro dans chacune d’elles ont été placés ensemble. Sur chaque îlot de la salle se trouvait donc en tout sept à huit élèves émanant des deux classes. Ils ont eu pour mission de se présenter successivement le mathématicien qu’ils avaient étudié.

Les présentations, intégralement en anglais bien sûr, nous ont souvent épatées par la qualité et la créativité dont les élèves ont fait preuve. Certains groupes avaient pour support un diaporama, d’autres avaient imaginé une mise en scène théâtrale en jouant les petits enfants de Dudeney, d’autres encore avaient monté un petit film et beaucoup d’entre eux avaient fabriqué des manipulations afin d’expliquer quelques énigmes qu’ils avaient eux-mêmes choisies. Les élèves se sont rapidement rendu compte des similitudes entre les vies et les travaux de ces deux hommes ce qui nous a permis de passer aisément à la deuxième partie du projet.
Deuxième étape : résolution et comparaison des énigmes
Après cette séance de présentation commune, nous avons retrouvé chacune de nos classes et avons donné à chacun des sept groupes une énigme de Dudeney pour les élèves d’Emmanuelle Pernot et de Sam Loyd pour les élèves de Fatih Pinar. Ces énigmes avaient été minutieusement choisies. En effet, les groupes ayant le même numéro dans chaque classe avaient des énigmes dont la résolution était similaire mais le contexte et la présentation différents1.
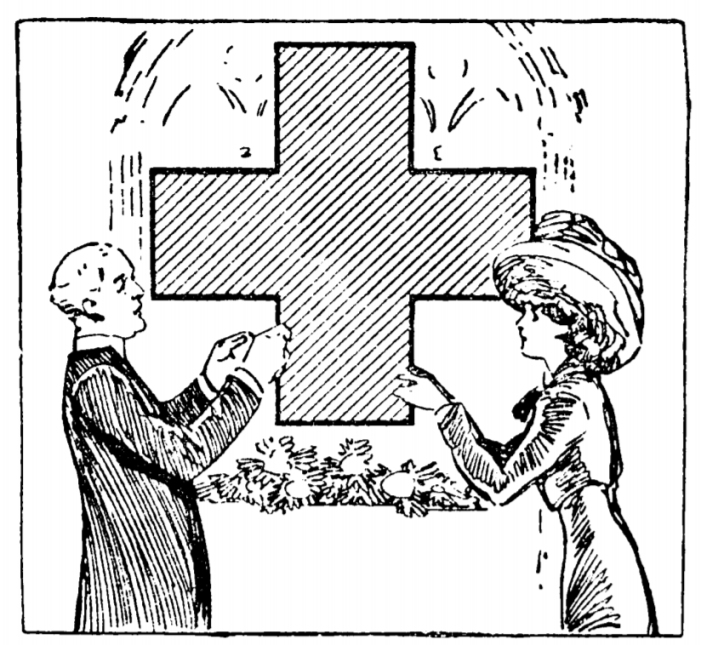
On peut remarquer que Sam Loyd a imaginé, pour la plupart de ses énigmes et puzzles, des contextes et des illustrations qui ont aidé à leur large popularisation aux États-Unis.
Par exemple, les énigmes des figures 1 et 2 ont été proposées aux deux groupes 4.
Ces deux énigmes proposent un problème de découpage pour obtenir une croix grecque. Chez Dudeney, l’énoncé est très sommaire tandis que chez Loyd, il est très contextualisé. Outre les similarités flagrantes entre les contextes, les énigmes sont également troublantes de ressemblance. Les élèves ont passé deux heures à résoudre les énigmes qui leur ont été confiées lors de la quatrième séance.

Figure 3. Résolution du riddle Red Cross Volunteers.

Figure 4. Résolution du riddle The Greek crosses.
Pour les deux groupes, la fabrication des pièces et la manipulation se sont imposées dans un premier temps pour résoudre ces puzzles. Cette technique s’est avérée concluante rapidement pour l’énigme de Sam Loyd. Néanmoins, l’énigme de Dudeney s’est avérée plus difficile à résoudre, le groupe a donc cherché à formaliser le problème par des figures géométriques au tableau.
L’objectif des élèves pour cette cinquième séance étape a alors été d’imaginer la création de supports permettant au groupe de l’autre classe (qui a une énigme similaire) de la résoudre. Sans aucune contrainte, certains ont imaginé un diaporama, quand d’autres sont allés jusqu’à créer du matériel de jeu.
Lors de la sixième séance, les deux classes ont été réunies pour la deuxième fois : les mêmes sept groupes de chaque classe ont été à nouveau confrontés. Ils ont eu pour consigne de présenter l’énigme qu’ils se sont vu attribuer, en demandant à l’autre groupe de la résoudre pour eux. Les échanges furent riches et consistants dans tous les îlots.

Figure 5. Échanges entre élèves des deux classes.
Certains groupes ont alors très vite remarqué des similarités flagrantes entre les énigmes.
Beaucoup d’élèves nous ont alors demandé s’il n’y avait pas de trucages, si les énigmes avaient été choisies volontairement… Nous sommes restés silencieux face à leurs interrogations afin de ne pas orienter leur réflexion. Les élèves ayant étudié la vie de H. Dudeney se sont souvenus que durant sa vie, Dudeney avait accusé Loyd de plagiat. La dernière étape s’est donc imposée d’elle-même tout naturellement : les élèves de Mme Pernot ont crié au scandale !
Troisième étape : le procès
Au départ, nous voulions organiser un débat en anglais entre les deux classes. Mais l’idée d’organiser un procès — ce procès que Dudeney aurait pu intenter à Loyd (et qui n’a jamais eu lieu) — est venue comme une évidence. Nous avons alors laissé aux élèves trois heures pour préparer ce dernier (sur deux séances). Chaque classe revenue avec son professeur respectif, a désigné des élèves pour des rôles : nous avons eu très vite un «Loyd» et un «Dudeney», des avocats, des jurés, un greffier, des témoins pour chaque partie, des illustrateurs, des cameramen, des agents de sécurité… Les rôles ayant été distribués, il a ensuite fallu constituer les plaidoiries, les arguments des deux candidats. Nous avons laissé une totale liberté aux élèves pour organiser la défense de leur mathématicien. Ils ont cependant eu besoin d’indications sur les formulations d’usage du droit anglo-saxon ainsi que sur le déroulement d’un procès. Aussi, des arguments parfois farfelus ont vu le jour, mais la préparation de ce procès a été passionnante quoique difficile, compte-tenu du temps imparti aux élèves.
Lors de la dernière séance (la neuvième), un procès d’une heure s’est déroulé. Trois de nos collègues, intervenant également en section européenne et n’ayant eu vent que de loin de cette affaire, ont fait office de juges.

Figure 6. Le procès.
L’accusation démarra avec une plaidoirie rondement menée par les avocats de Dudeney. Puis, la plaidoirie de la défense ne s’est pas faite attendre très longtemps, et nous sommes vite passés aux témoignages. Chaque partie a fait appel à ses témoins et a avancé ses preuves. Une théorie comme quoi la femme de Dudeney aurait comploté dans son dos pour transmettre les travaux de son mari à Loyd est née, quand la partie adverse récusait ceci en affirmant que le fils de Dudeney aurait séduit la fille de Loyd pour lui voler ses travaux. Il y a eu également des contre-interrogatoires, parfois déstabilisants pour les témoins. Le procès en lui-même s’est conclu et les jurés se sont retirés pour délibérer. Après quelques minutes (le temps était court), les juges et les jurés sont revenus dans la salle du tribunal pour prononcer le verdict. Loyd a été déclaré coupable de plagiat.
Quatrième étape : les réactions
Chaque groupe a ensuite rédigé un petit résumé de leur ressenti sur le procès, qui a ensuite été publié sur le site du lycée ![]() .
.
Du point de vue des plaignants, les Terminales euro math de Mme Pernot
Notre classe a participé à un projet, celui de défendre M. Dudeney qui a été victime d’une terrible injustice. Son ancien ami, ce traître de Loyd, lui a volé ses travaux. Ils se sont donc affrontés dans un procès où l’ambiance était très tendue. Grâce à nos avocats très compétents, nous avons pu écraser la défense adverse. Nos preuves irréfutables et nos témoins nous garantissaient une longueur d’avance sur nos adversaires. Nous avons réussi à convaincre les jurés car la défense adverse était insuffisamment préparée. Bien entendu, tout cela dans un calme assuré par la sécurité.
Du point de vue de la défense, les Terminales euro math de M. Pinar
Les arguments des avocats du plaignant étaient toujours les mêmes. Chaque témoin avançait la même chose que le précédent. Les avocats de Dudeney ont très probablement inventé une fausse histoire dans laquelle Loyd était ivre, sans être capable de le prouver, Loyd ayant lui déclaré qu’il ne buvait jamais. Il a été question d’une lettre écrite par M Dudeney mais nous n’avons jamais vu cette lettre, elle aurait soi-disant disparu. De plus, Dudeney n’a pas répondu aux questions des avocats de la défense. Certains jurés lors de la délibération étaient par ailleurs probablement corrompus. Pour conclure, nos avocats sont formels, la partie adverse n’a jamais fourni de preuves de la culpabilité de Loyd.
Bilan du projet
Cette séquence a été pour nous une formidable opportunité de faire des mathématiques de manière ludique et intéressante linguistiquement. En effet, le but de la SELO est de permettre aux élèves de pratiquer une discipline non linguistique dans une langue étrangère. Ici, entre les énigmes mathématiques en anglais et le procès, qui s’est déroulé exclusivement en anglais, le contrat a été parfaitement rempli. Les élèves ont tout de suite adhéré au projet, et ont vraiment apprécié cette séquence dans son intégralité. Dans l’imaginaire collectif, et même dans celui des élèves aujourd’hui, quand on pense aux mathématiques, on pense au cours magistral peu passionnant. Pouvoir faire des mathématiques de cette manière, et qui plus est, en travaillant une langue étrangère et en permettant aux élèves d’interagir, de confronter des idées, des raisonnements et des arguments, est quelque chose de très gratifiant, que ce soit pour nous les professeurs ou pour les élèves. Ces derniers nous ont chaleureusement remerciés de leur avoir permis de participer à un tel projet, qu’ils ont même, pour certains, évoqué avec enthousiasme lors de leur oral de SELO au baccalauréat. Notre bilan en tant que professeurs est extrêmement positif, l’implication et l’intérêt que les élèves ont pu montrer vis à vis de ce projet nous ont poussé à aller au-delà des objectifs que nous nous étions initialement fixés.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Emmanuelle Pernot et Fatih Pinar (n’hésitez pas à consulter sa chaîne Youtube
) étaient professeurs au lycée Janot de Sens dans l’académie de Dijon au moment de la réalisation de ce projet. Emmanuelle Pernot exerce actuellement au lycée français international d’Ibiza.
![]()
![]()
-
Les différentes énigmes se trouvent dans la revue en ligne .
 ↩
↩