Meurtres à Numbertown
L’histoire d’une coopération, à deux, à vingt-quatre, et bien plus encore. L’histoire aussi de « comment l’envie de partager une partie du travail de préparation entre deux enseignants de Seconde a donné lieu à une coopération beaucoup plus étendue qu’attendue. »
Élodie Henriet et Rhydwen Volsik
© APMEP Décembre 2019
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Mars 1848. Deux vaillants enquêteurs, Ada Lovelace, de la police mathématique de Numbertown, et Jules Verne, un jeune romancier en quête d’aventures, sont missionnés pour résoudre une sordide affaire de triple meurtre.
Septembre 2018. Deux vaillants professeurs se sont donné comme mission de faire revivre à leurs élèves de Seconde du « Colegio Julio Verne » au Guatemala la traque du plus grand criminel de l’histoire de Numbertown.
Année 2018-2019. Deux classes de vaillants élèves ont coopéré pour poursuivre le meurtrier de Numbertown à New-York, en passant par l’île Chairman. Sans faillir, ils sont allés jusqu’au bout de l’enquête et ont réussi à ramener le coupable devant ses juges.
En quatorze devoirs maison, les élèves ont donc pu admirer les idées et la détermination d’Ada1, vivre les doutes et les inquiétudes des enquêteurs au fur et à mesure des rebondissements, et récolter de précieux indices. Mais ils ont aussi épaulé la police mathématique en réparant leur machine à café et aidé Jules à compléter sa culture mathématique, ce qui a pu se révéler encore plus utile que prévu.
Le contexte
Le lycée Jules Verne, établissement conventionné de l’AEFE2 au Guatemala, est un établissement qui compte environ 1000 élèves (de la maternelle au lycée). Les deux classes de Seconde comptaient cette année 23 élèves, la plupart ne venant pas de familles francophones. Leur pratique du français est donc souvent limitée aux heures de cours. De notre côté, nouveaux dans l’établissement, nous avions une forte envie de profiter de ce changement de contexte pour mettre en pratique des idées de projets, méthodes pédagogiques… glanées ici et là depuis des années. Mais pour cela, il nous fallait dégager du temps, et quoi de mieux pour y parvenir que de partager le travail. Nous nous sommes répartis les rôles et les tâches, pour la préparation des cours, des TP et des évaluations, mais aussi le choix des exercices et des DM.
Le risque était non nul que cette collaboration explose en plein vol, que nous ne soyons pas du tout d’accord sur certains principes fondamentaux. Après tout, coopérer c’est accepter de s’exposer, au risque de se sentir jugé. Et puis comment noter les DM, comment évaluer les TP, spiraler or not spiraler, l’un d’entre nous allait-il prendre trois semaines d’avance sur la progression commune en un trimestre ? Mais le feeling était bon, comme on dit, c’était donc vraiment l’occasion de se lancer.
Finalement, aucune de ces craintes ne s’est révélée fondée. Mieux encore, le travail collaboratif entre professeurs s’est étendu. D’abord parce qu’un projet de voyage de classe à New-York nous a amenés à collaborer aussi avec les professeurs responsables de ce voyage (anglais et histoire-géographie) et à faire référence dans nos DM à cette ville (qui devient la cachette finale du tueur). Mais aussi parce que la professeure de français des deux classes de Seconde, Christelle Touleron, a décidé de faire travailler les élèves en AP3 sur différents aspects de l’enquête. Ainsi les élèves ont commencé par rédiger soit un rapport d’enquête, soit une interview des personnes présentes sur la scène de crime, puis plus tard ils ont proposé un portrait psychologique du tueur, basé sur les différentes découvertes faites au fur et à mesure des DM.
Les échanges liés à la préparation des cours, TP et DS, se sont révélés très enrichissants et nous avons beaucoup appris l’un de l’autre pendant ces quelques mois.
La fabrique des DM
Pour illustrer un peu plus précisément notre fonctionnement d’équipe, nous allons vous parler de l’élaboration des devoirs maison. Notre idée initiale était donc de raconter une histoire : celle d’un tueur de nombres dans la ville de Numbertown, d’habitude si tranquille.
Voici quelques objectifs que nous nous sommes fixés :
-
maintenir la même trame narrative, le suspense et la tension toute l’année : cela oblige à penser dès le départ la fin de l’histoire. Dans notre cas, nous avons choisi dès le début la méthode de cryptographie qui devait permettre, dans le dernier DM, d’obtenir le nom du coupable à partir des nombres récoltés en cours de route ;
-
garder une vraie liberté pour les thèmes abordés dans chaque DM (les deux premiers concernent les écritures de nombres et de fractions chez les Mayas et les Égyptiens), mais aussi essayer de tisser des liens avec le reste des activités faites en classe, ou des exercices donnés en évaluation ;
-
faire travailler l’algorithmique et l’utilisation de
Python; -
personnaliser le plus possible les devoirs, en donnant le même sujet mais avec des données différentes, afin de limiter la recopie et de favoriser le travail d’équipe.
Pour le dernier point, cela s’est révélé plus compliqué et chronophage que prévu, et ce n’est qu’à la fin de l’année, en particulier grâce aux progrès de nos élèves en Python, que nous avons pu y parvenir.
Créer du lien, nous l’avons par exemple envisagé sous la forme d’un TP au cours duquel il fallait modéliser le château des Bories (en Dordogne) sous GeoGebra4, voir la figure 1, suivi plus tard d’un DM (figure 2) dans lequel Jules doit, pour obtenir une liste de suspects, aller rencontrer le président de l’« Association Internationale des Mathématiciens », qui se trouve être le propriétaire (peu chaleureux) de ce château, et qui accepte de lui donner cette liste à condition qu’il fasse preuve de ses connaissances mathématiques.
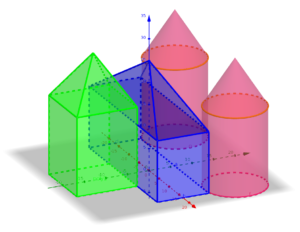
Figure 1. La figure obtenue en TP. ↩
|
Voilà, Ada dispose maintenant d’une liste de 23 adresses à New-York, il ne lui reste plus qu’à s’y rendre avec ses détectives. |
Figure 2. Le début du DM 13. ↩
Les clefs du succès
Monica Gather Thurler et Philippe Perrenoud, dans la revue Recherche & Formation [1] se sont demandé en quoi consisterait une formation professionnelle à la coopération.
Des six traits qu’ils proposent, nous voudrions revenir sur les trois premiers :
-
se rendre compte que la coopération n’est pas la figure dominante de la professionnalité enseignante ;
-
ne pas confondre coopération et affinités électives ;
-
entretenir un rapport utilitariste et sélectif à la coopération.
Il nous semble effectivement très clair que nous manquons de formation dans ce domaine et que la culpabilisation vient vite lorsqu’on pense qu’il faudrait que la coopération soit naturelle et immédiate, alors que c’est très rarement le cas. Il nous semble que l’administration de chaque établissement peut jouer un rôle d’émulation dans ce domaine, par exemple en plaçant une heure de concertation dans l’emploi du temps de tous les professeurs de l’équipe disciplinaire, ou encore en mettant au moins une heure en parallèle dans les emplois du temps d’un même niveau (par exemple pour des contrôles communs)5.
Le deuxième point est fortement lié au premier : si vraiment on souhaite dépasser le classique duo amitié-coopération, il nous semble que les incitations institutionnelles devront être beaucoup plus fortes. En effet, les incantations à travailler ensemble risquent d’être inaudibles si une forme de valorisation de ce travail n’est pas proposée aux professeurs déjà surchargés, par exemple en réduisant les effectifs dans les classes. Et si, par exemple, on trouvait le moyen de financer au moins une partie de ces heures de concertation et d’échanges de pratiques ?
Concernant le troisième point (« entretenir un rapport utilitariste et sélectif à la coopération ») il faut aussi veiller à ce que la coopération soit un investissement, afin d’améliorer nos pratiques pédagogiques ou afin de gagner du temps (ces deux objectifs sont peut-être plus liés qu’on ne le pense). Les auteurs n’hésitent pas à dire qu’une collaboration qui n’apporte pas de bénéfice doit être abandonnée.
Pour revenir à notre situation personnelle, voici ce qui, rétrospectivement, nous semble avoir permis à cette coopération d’être aussi efficace et de perdurer tout au long de l’année :
-
nous sommes voisins, ni l’un ni l’autre n’avions cours le lundi, ce qui nous a permis de nous voir en moyenne tous les 15 jours, pour une durée d’environ 3-4 heures, dont souvent un minimum de 2 heures consacrées aux DM ;
-
nous avons bien réparti les tâches, en particulier l’écriture et la relecture des énoncés et la rédaction des corrigés, avec une confiance qui n’a pas failli durant toute l’année ;
-
nous avons des parcours, des pratiques, des préférences et des compétences finalement assez différents, ce qui nous a rendus très complémentaires et nous a sans doute vraiment aidés à bien nous entendre (dans le sens d’être à l’écoute) ;
-
nous avons organisé notre travail selon un planning finalement assez immuable :
- pendant la « séance du lundi », nous faisions le bilan des semaines précédentes et confirmions la progression envisagée en début d’année, avant de répartir les tâches pour les jours et semaines à venir ;
-
chacun réalisait alors les documents et préparations auxquels il s’était engagé ;
-
l’autre pouvait alors proposer les modifications et corrections avant mise en application avec les élèves.
-
grâce au temps gagné par ce partage de tâches, nous avons pu vivre la satisfaction de mettre en pratique des idées et projets que nous n’avions jamais pu faire vivre jusque-là, en général par manque de temps de préparation ;
-
nos élèves ont un accès facile à internet en général, à l’ENT de l’établissement et au site repl.it6
 en particulier;
en particulier; -
en parallèle de ces DM, les élèves devaient résoudre, au fur et à mesure de l’année, les problèmes du cours sur
Pythonde l’association France-IOI .
.
De la coopération entre élèves
Un des problèmes usuels des devoirs maison est la recopie (ou également l’aide trop importante d’une tierce personne — l’article d’Antoine Laniray dans le numéro 531 d’Au Fil des Maths évoquait récemment cette difficulté). Comme indiqué plus haut, la solution que nous avons pu mettre en œuvre à la fin de l’année a été de donner le même devoir à tous les élèves, mais en changeant les données du problème, de façon à ce que le travail de chacun soit nécessaire à l’assemblage du puzzle-réponse.
Ainsi, dans le devoir 10 (du mois de février), il s’agissait d’utiliser la technique du pixel-art pour reconstituer le portrait robot du tueur (figure 3). Chaque élève disposait du code d’un vingt-quatrième du portrait, et ce n’est que lorsque tous les élèves ont réussi à reconstituer leur image que le portrait dans son ensemble a pu être affiché dans la salle de classe.
Un peu plus tard, les élèves ayant eu de nombreuses occasions de progresser en Python, nous avons pu mettre en pratique une idée qui nous tentait depuis longtemps : effectuer sur des romans écrits en différentes langues une étude statistique afin de comparer les pourcentages d’apparition des lettres de l’alphabet. Nous avons donc effectué une sélection de romans en français, espagnol, anglais et allemand, puis nous avons envoyé à chacun des élèves un des romans via l’ENT. Grâce à leurs connaissances en Python, ils ont pu compléter un programme afin d’obtenir la fréquence de chaque lettre.


Figure 3. Le portrait robot en pixel-art, avec détail. ↩
Sur une carte de New-York (figure 4), les élèves ont alors obtenu 23 points dont les coordonnées correspondent aux fréquences des lettres a et o de chaque roman. Avec les informations récoltées dans le DM suivant, il ne restait plus à nos apprentis détectives qu’à faire leur voyage de classe à New-York pour ramener à Numbertown, sous l’autorité d’Ada Lovelace, sinon le coupable, au moins les 23 suspects (ou plutôt 18, nos enquêteurs ayant déjà établi qu’il s’agissait d’un homme).
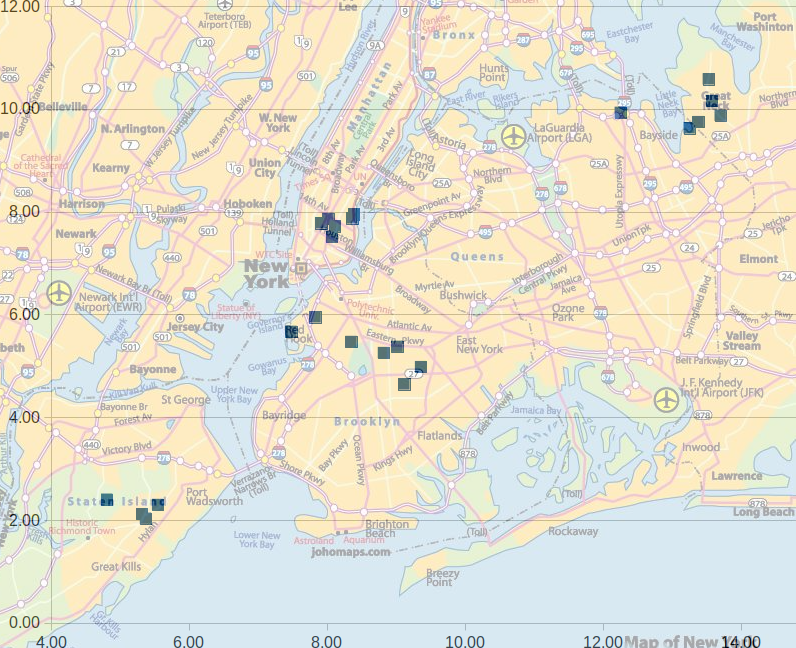
Figure 4. Carte de New-York avec les cachettes possibles du tueur7. ↩

Conclusion
À l’heure où nous écrivons ces lignes, les élèves ont trouvé le coupable (peut-être l’avez-vous reconnu sur son portrait robot ?). Ramené à Numbertown, il devra maintenant faire face à ses juges, lors d’un procès mené par les élèves. Ils auront à leur disposition tous les éléments découverts dans les DM, mais aussi des rapports d’enquêtes et des éléments du profil psychologique du meurtrier rédigés pendant leurs cours de français.
Pour nous, c’est l’heure des perspectives pour l’année prochaine. D’abord nous aimerions développer le travail en commun avec les collègues d’autres disciplines, en particulier de Lettres. Nous voudrions aussi augmenter le nombre de travaux dont les données sont individuelles. S’il faut bien admettre que ce travail demande beaucoup de temps (sans notre coopération, qui nous a permis d’en gagner de façon substantielle, rien de tout cela n’aurait été possible), il est extrêmement satisfaisant de voir les élèves jouer le jeu et apporter chacun leur pierre à la construction de la solution du problème.
|
Et puis, étant donné que l’histoire des mathématiques prend une place encore plus importante dans le nouveau programme, nous voudrions mettre en œuvre de façon plus performante et mémorable les exposés que nos élèves ont faits sur les différents personnages historiques croisés lors de l’enquête. La réalisation de petites vidéos, d’interviews, de débats…sont des pistes que nous comptons travailler l’année prochaine pour rendre cette histoire des mathématiques bien vivante. |
Enfin, la mise en place d’un escape game interdisciplinaire est un objectif auquel nous tenons beaucoup tous les deux. Nous verrons bien ce que la mise en place de la réforme du lycée nous laissera comme temps pour développer nos pratiques pédagogiques !
Référence
-
Monica Thurler Gather et Perrenoud Philippe. « Coopération entre enseignants : la formation initiale doit-elle devancer les pratiques ?
 ». In : Recherche & Formation no 49 (2005), p. 91-105. ↩
». In : Recherche & Formation no 49 (2005), p. 91-105. ↩
L’ensemble des DM est disponible sur le site number.town.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Adhérent de l’APMEP depuis sa première année d’enseignement, Rhydwen Volsik a débuté sa carrière dans des lycées de l’académie de Créteil. Il a été responsable des sections européennes à l’APMEP avant de partir à l’étranger.
Élodie Henriet vient de Franche-Comté où elle a majoritairement enseigné en collège.
Les deux auteurs se sont rencontrés en septembre 2018 au lycée français du Guatemala.
-
Forcément, une certaine familiarité s’est installée avec les héros de notre histoire. ↩
-
Agence pour l’enseignement français à l’étranger. ↩
-
Accompagnement Personnalisé. ↩
-
L’idée de cette activité vient peut-être d’un manuel, mais nous n’avons pas réussi à retrouver la source. ↩
-
C’est sans doute plus facile à dire qu’à faire, nous en avons bien conscience. ↩
-
Ce site fera l’objet d’un coup de cœur dans un prochain numéro d’Au fil des maths. ↩
-
Saurez-vous associer chaque langue des romans distribués aux élèves à l’un des quartiers de la ville
 ? ↩
? ↩
