Un débat à propos d’ensembles infinis
En complément de son article paru dans la revue papier n° 542, Thérèse Gilbert nous présente un exemple de « débat prévu » vécu en formation d’enseignants en Belgique.
Thérèse Gilbert
© APMEP Décembre 2021
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Le débat qui suit a lieu en Bac 3, en formation d’enseignants1, à la première séance d’un cours sur les cardinaux infinis et tient lieu d’introduction au sujet. Depuis deux ans, les étudiants ont profité de pas mal d’occasions pour conjecturer et débattre.
Les règles du débat ont déjà été énoncées ou rappelées lors d’un atelier sur le débat, quelques semaines avant (voir aussi M. Legrand [4]) :
-
chacun peut (mais personne ne doit) prendre la parole ;
-
on s’exprime pour être entendu de tous, on se tourne vers ses condisciples, on les regarde ;
-
on annonce la thèse que l’on défend avant de l’argumenter ;
-
chacun est soucieux de connaître l’avis des autres et regarde celui qui s’exprime ;
-
on réagit sans détour mais avec respect ;
-
on peut aussi rejoindre la position d’un autre participant en ajoutant un nouvel argument ou une explication différente ;
-
on s’interdit les arguments d’autorité : « C’est comme ça parce qu’untel l’a dit », « En maths, on fait toujours comme ça » …
Voici la consigne2.
|
On se donne les ensembles suivants :
Comparez la taille de ces ensembles. |
Après un petit temps de réflexion individuelle et une brève discussion en petits groupes, les étudiants — ils sont dix — proposent trois solutions : par ordre décroissant de taille,
-
\(\mathbb{Z}\) ; \(\qquad\mathbb{N}\), \(A\) et \(B\) ; \(\qquad\mathbb{Z}^-_0\) ; \(\qquad2\mathbb{N}\) ;
-
tous ont la même taille ;
-
\(\mathbb{Z}\) ; \(\qquad\mathbb{N}\) ; \(\qquad2\mathbb{N}\) ; \(\qquad A\) ; \(\qquad B\) ; \(\qquad\mathbb{Z}^-_0\).
Ils votent. Les voix sont surtout réparties entre les solutions 1 et 2.
Le débat peut commencer… Il a duré 45 minutes et a été enregistré. En voici des extraits dans l’ordre chronologique, mais structurés en fonction des arguments, et augmentés de l’un ou l’autre commentaire en italique et en couleur.
Quelques extraits du débat
Les ensembles ont tous la même taille car ils sont tous infinis
- Nadir
-
Je place 0 dans \(\mathbb{N}\) et 0 dans \(\mathbb{Z}\), puis 1 dans \(\mathbb{N}\) et 1 dans \(\mathbb{Z}\), et puis 2 et 2… Donc ces deux ensembles sont de même taille, chaque fois que j’ajoute un nombre dans un ensemble, de l’autre côté, je vais faire pareil. Contre-argument ?
- Laure
-
D’accord tu ajoutes dans \(\mathbb{N}\) et puis tu ajoutes dans \(\mathbb{Z}\). Mais, si tu commences par ajouter dans \(\mathbb{Z}\) ?
- Nadir
-
Si j’ajoute \(-1\) dans \(\mathbb{Z}\), eh bien, j’ajoute 4 dans \(\mathbb{N}\).
- Laure
-
Oui, mais si tu ajoutes 4 dans \(\mathbb{Z}\).
- Nadir
-
C’est pas un problème. Je n’ai pas dit que j’ajoutais le même. J’ajoute 5 dans \(\mathbb{N}\). Il y a plein de nombres, ça va jusqu’à l’infini.
L’inclusion pour comparer les tailles
- Jassem
-
Tous les nombres qui sont dans l’ensemble des naturels sont aussi dans l’ensemble des entiers, mais il y a des nombres dans l’ensemble des entiers qui ne sont pas dans les naturels. Donc il y a plus de nombres entiers.
- Nadir
-
Si je te demande « Combien y a-t-il de nombres dans l’ensemble des naturels », tu dis quoi ?
- Jassem
-
Une infinité.
- Nadir
-
Et dans l’ensemble des entiers ?
- Jassem
-
Une infinité.
- Nadir
-
Compare ces deux nombres.
- Jassem
-
D’accord, j’ai compris. Mais s’il y a deux groupes d’élèves, un avec les mêmes élèves que dans l’autre, mais avec des élèves en plus. Dans quel groupe il y aura le plus d’élèves ?
Peut-on raisonner sur les ensembles infinis comme on le fait sur les ensembles finis ?
- Farah
-
Là, tu prends un cas où il y a un nombre fini d’élèves. Ici on est dans l’infini. Il n’y a pas d’infini plus grand qu’un autre infini.
Comment trancher ?
- Bruno
-
Je suis d’accord avec les deux avis. Je ne peux pas contredire l’un ou l’autre.
- Djamila
-
Moi aussi.
- Iona
-
Je suis du même avis que Bruno. Chaque ensemble a un nombre infini d’éléments, mais il y a des ensembles inclus dans un autre et c’est cela qui me frustre. Je me demande si on peut classer des infinis. Je trouve cela un peu bizarre et je suis partagée.
L’infini produit une situation inédite. On a envie de penser deux choses apparemment contradictoires : deux ensembles pourraient avoir même taille d’un certain point de vue (ils sont infinis) et deux tailles différentes d’un autre point de vue (l’un est strictement inclus dans l’autre).
Un argument issu du calcul de limites : \(2\cdot\infty=\infty\)
- Bruno
-
On peut voir dans les entiers deux formes de l’ensemble des naturels : les naturels positifs et les « naturels négatifs », on va dire. C’est comme s’il y avait deux infinis dans les entiers. Mais en humanités, on a toujours appris que deux fois l’infini, c’est égal à l’infini.
L’injection non bijective qui remplace l’inclusion stricte
- Jassem
-
(au tableau)

Chaque élément de \(\mathbb{N}\) va avoir une relation unique avec un élément de \(\mathbb{Z}\). Sauf que les éléments négatifs ne vont pas avoir de relation dans \(\mathbb{Z}\). Il y aura plus d’éléments.
- Nadir
-
Mais tu n’auras jamais fini d’associer des positifs. Donc tu n’auras pas le temps d’aller vers \(-1\), \(-2\), etc.
- Jassem
-
On va créer des binômes sauf qu’il y aura ces éléments-là [il montre les négatifs] qui n’auront pas de correspondant.
On voit aussi se confronter une vision de l’infini potentiel « on n’arrivera jamais au bout » et de l’infini actuel « on associe tout élément d’un ensemble à un élément de l’autre ensemble à l’aide d’une application ».
Comparer les ensembles sur des intervalles
Dylan regarde les ensembles sur des intervalles. Il compte combien d’éléments de chaque ensemble appartiennent aux intervalles choisis. Le tableau suivant permet de comprendre le principe.
\[\begin{array}{l|cc}
&[0\,;\,100]&[-50\,;\,50]\\
\hline
\mathbb{Z} &101&101\\
\mathbb{N} &101&51\\
2\mathbb{N} &51&26\\
A &11&8\\
B &5&4\\
\mathbb{Z}_0^- &1&51
\end{array}\]
- Dylan
-
C’est sur la base de ça que j’ai ordonné les ensembles [solution 3]. Le classement va changer [d’un intervalle à l’autre], mais \(\mathbb{Z}\) reste l’ensemble prédominant.
- Farah
-
C’est comme avec Jassem, avec les groupes d’élèves. On prend toujours un nombre fini d’éléments et pas un nombre infini.
- Dylan
-
On pourrait faire une infinité d’intervalles… Mais \(\mathbb{Z}\) est celui dans lequel il y a le plus d’éléments.
- Jassem
-
Ça me paraît compliqué. Je ne dis pas que c’est faux. Mais ça me paraît compliqué.
Pour appréhender l’infini, on regarde les ensembles par morceaux, mais en envisageant une infinité de morceaux. Une autre méthode, entendue une autre année, consiste à élargir un intervalle de départ \([-n\,;\,n]\) en faisant tendre \(n\) vers3 l’infini.
Une injection qui ne correspond pas à une inclusion
- Iona
-
Un naturel a toujours son opposé. Donc l’ensemble des entiers négatifs a le même nombre [d’éléments] que l’ensemble des naturels mais un de moins.
Une bijection « naturelle »
Jassem montre une correspondance entre \(\mathbb{N}\) et \(A\) [l’ensemble des carrés parfaits].
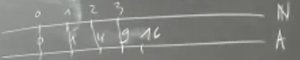
Et c’est la même chose pour \(B\) [l’ensemble des cubes parfaits positifs].
Maintenant qu’on a vu que \(\mathbb{N}\) et \(A\) ont même taille, on peut aussi dire que \(\mathbb{N}\) et \(\mathbb{Z}\) ont même taille.
Sauf que, dans \(A\), chaque nombre a une correspondance unique avec un nombre dans \(\mathbb{N}\), alors que, dans \(\mathbb{Z}\), non.
L’existence d’une bijection « quelconque »
- Farah
-
Mais dans \(\mathbb{Z}\), on va pouvoir trouver un autre stratagème, comme tu fais là.
- Jassem
-
C’est pas un stratagème.
- Farah
-
Oui, mais tu ne fais pas correspondre 2 avec 2, tu fais correspondre 2 avec un autre nombre.
- Jassem
-
Oui, c’est une relation qui existe entre ces deux nombres-là.
- Bruno
-
Il y a [aussi] une relation entre \(\mathbb{N}\) et \(2\mathbb{N}\). On relie 0 avec 0, 1 avec 2, 2 avec 4, 3 avec 6… Pour chaque élément de \(\mathbb{N}\), il y a un élément de \(2\mathbb{N}\). Donc il faudrait mettre \(2\mathbb{N}\) dans le package de \(\mathbb{N}, A\) et \(B\).
- Nadir
-
Jassem, quand tu compares deux ensembles, tu trouves une relation ?
- Jassem
-
C’est pas moi qui décide.
- Nadir
-
Mais si, parce que, pour \(\mathbb{N}\) et \(A\), tu as décidé de mettre le 1 avec le 1, le 2 avec le 4, le 3 avec le 9…
- Jassem
-
Beh, c’est pas moi qui choisis. C’est pas moi qui ai dit « Alors je vais relier le 0 avec le 4 parce qu’aujourd’hui, il fait beau ».
Une application doit-elle sembler « naturelle » pour pouvoir être utilisée dans ce contexte ?
Farah suggère la correspondance suivante
\[\begin{array}{cccccccc}
0&1&-1&2&-2&3&-3&{\dots}\\
0&1&2&3&4 &5&6 &{\dots}\\
\end{array}\]
- Farah
-
On pourra toujours faire un lien. On pourra toujours faire pour les deux une infinité de colonnes. Il n’y aura pas plus de colonnes d’un côté que de l’autre.
Nadir fait un geste pour dire « cassé » à Jassem. Rires.
- Nadir
-
Non, mais elle a raison.
- Jassem
-
Mais comment… ?
- Farah
-
Je ne mets pas de lien de \(\times 2\) ou \(\times 3\). Je les note juste dans l’ordre. J’ai trouvé une technique pour que le fait qu’il y ait des négatifs et des positifs soit moins perturbant. Avec cette écriture, on aura tous les positifs et tous les négatifs, et on pourra faire correspondre un nombre de \(\mathbb{N}\) avec un nombre de \(\mathbb{Z}\), puisqu’on ne s’arrête jamais d’écrire.
On change l’ordre naturel de \(\mathbb{Z}\) et on ne s’occupe plus de trouver une application qui semble « naturelle », on s’assure juste de l’existence d’une bijection pour comparer certains ensembles.
- Nadir
-
C’est comme quand tu fais des rangs. Tu cherches pas à savoir si c’est une fille ou un garçon…
- Farah
-
Comme Jassem est venu avec son argument de faire des liens, moi je montre qu’on peut quand même faire des liens et montrer que c’est l’infini [qu’ils ont tous la même taille].
- Prof
-
Donc on se demande si on ne pourrait pas mettre \(\mathbb{Z}\) avec \(\mathbb{N}\), \(A\), \(B\), \(2\mathbb{N}\) ?
- Farah
-
Et les négatifs…
Ikram donne la relation suggérée par le tableau suivant : \[
\begin{array}{ccccccc}
0& 1& 2& 3& 4& 5& {\dots}\\
-1& -2& -3& -4& -5& -6& {\dots}
\end{array}\]
La comparaison à l’aide de la bijection se heurte à l’inclusion stricte
- Jassem
-
J’ai un contre-exemple. Avec la logique de Farah, les ensembles \(\mathbb{N}\) et \(\mathbb{N}_0\) ont le même nombre d’éléments alors qu’on en a retiré un.
- Farah
-
Oui.
- Prof
-
C’est violent, quoi ?
- Jassem
-
Et, avec cette logique-là, on peut continuer et se dire « Jusqu’où on peut aller ? ».
Conclusion
Dernières propositions de réponse et dernier vote. Les solutions ont évolué mais les avis sont encore partagés.
-
Tous de même taille (4 voix) ;
-
\(\mathbb{Z}\) ; \(\qquad\mathbb{N}\), \(A, B\), 2\(\mathbb{N}\) ; \(\qquad\mathbb{Z}^-_0\) (3 voix) ;
-
les deux ordres à la fois (3 voix).
Je clos le débat : selon la définition de « taille » que l’on choisit, on n’arrivera pas à la même réponse. Je reprends les principaux arguments utilisés et les situe par rapport au concept d’ordre (total ou non), aux conclusions de Galilée [2] (« Les attributs “égal”, “plus grand” et “plus petit” n’ont pas de sens pour les quantités infinies, mais seulement pour les quantités finies »), mais aussi par rapport à ce que nous allons faire, à la définition d’ensemble infini de Dedekind, à la définition de cardinaux de Cantor…
Les démarches mentales
Le débat s’est déroulé « presque sans moi ». Les étudiants s’adressent à leurs pairs (et non à moi) pour tenter de les convaincre, ils essaient d’être clairs, mais surtout ils s’écoutent. Ils utilisent les arguments des uns pour revoir leur point de vue, pour aller plus loin ou, parfois, pour les tourner à leur avantage.
Mon rôle, durant le débat, a surtout consisté à m’assurer des bonnes conditions spatiales (chacun doit pouvoir voir chacun), à demander parfois d’expliciter, d’écrire au tableau, parfois à donner la parole et décider des divers moments de vote. À la fin, j’ai fait le point sur les arguments développés et, au cours suivant, sur les démarches mentales utilisées et transférables :
-
s’exprimer, s’écouter, s’approprier les arguments des autres ;
-
rechercher un contre-exemple pour contredire un argument ;
-
évoquer des situations de la vie réelle (groupes d’élèves, rangs) ;
-
évoquer des cas que l’on connaît mieux (ensembles finis) ;
-
appliquer un argument à un cas pour arriver à quelque chose de contre-intuitif ;
-
utiliser l’argument d’un autre (avec lequel on n’est pas d’accord) pour l’appliquer autrement et convaincre ;
-
formuler ce qui coince…
Références
- H. Ben Aïcha, Des élèves dignes de grands mathématiciens !, in Traces de changements, n° 241, mai et juin 2019.
- G. Galilée, Discours et démonstrations mathématiques concernant deux sciences nouvelles, trad. M. Clavelin, Armand Colin, Paris, 1970.
- Th. Gilbert, Comparaison de carrelages et d’ensembles infinis, in Losanges n°49, Mons, 2020.
- M. Legrand, T. Lecorre, L. Leroux, A. Parreau, Principe du « Débat scientifique » dans un enseignement, Pré-tirage du Tome I, Journées nationales de l’APMEP Grenoble, novembre 2011, IREM de Grenoble.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Thérèse Gilbert est formatrice d’enseignants à la Haute École Galilée à Bruxelles et membre du Groupe d’Enseignement Mathématique (GEM,
) de Louvain-la-Neuve.
- Avec en partie les mêmes étudiants que ceux dont il est question dans Th. Gilbert, Apprendre à débattre et à animer un débat mathématique, Au fil des maths n°542, 2021.↩︎
- Pour un écho d’un débat sur une question similaire avec des élèves de 13 ans, voir H. Ben Aïcha, Des élèves dignes de grands mathématiciens ! [1].↩︎
-
Voir à ce propos Th. Gilbert, Comparaison de carrelages et d’ensembles infinis [3].↩︎
