Un tour de magie en CM2
Proposer un tour de magie mathématique pour offrir à des élèves une expérience d’apprentissage vivante autour des compétences de calcul à acquérir au cycle 3 : voilà une idée originale ! Les auteures présentent un travail réalisé dans deux classes de CM2.
Sarah Leleu Maati & Mathilde Scandolari
© APMEP Juin 2022
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Un tour de magie historique
Nous avons choisi de travailler à partir d’un tour de magie (deviner un nombre pensé) issu des Récréations mathématiques et physiques de Jacques Ozanam (1694).
L’activité a été présentée aux élèves comme un défi et a été prétexte à des manipulations arithmétiques. Les séances ont été menées durant plusieurs semaines.
La séquence qui suit a déjà été évoquée dans « Fonctions : une perspective historique » (MathémaTICE n°75 – mai 2021 ![]() ) et a été élaborée avec l’aide de Bernard Ycart, dont les « Histoires »
) et a été élaborée avec l’aide de Bernard Ycart, dont les « Histoires » ![]() nous ont largement ouvert les portes du monde mathématique.
nous ont largement ouvert les portes du monde mathématique.
Dans cet article, nous exposerons notre démarche pédagogique : comment aborder cette activité avec les enfants ? Comment mener les séances, de la manipulation de l’algorithme à l’écriture des calculs, en passant par la découverte de la notion d’inconnue ? Puis nous rendrons compte des évaluations qui ont été faites à l’issue de la séquence auprès des enfants.
Découverte du tour de magie
Le défi
L’objectif est de faire entrer d’emblée les enfants dans une activité ludique, «hors-cadre», qu’ils soient intéressés, intrigués, qu’ils aient à peine l’impression de travailler ; de quoi lever l’appréhension peut-être déjà liée aux apprentissages, et en particulier à celui des mathématiques.
La consigne suivante est donnée aux enfants.
|
Chaque enfant donne le résultat de son calcul, le tout est noté au tableau. Notre coach en maths, Bernard Ycart, est mis au défi de retrouver le nombre auquel chaque élève a pensé.

Mission accomplie après l’heure du déjeuner. Les enfants sont épatés, sauf quelques-uns, qui par pur esprit de contradiction, prétendent que «c’est trop facile !». Si c’est si facile… essayons !
En cherchant comment faire, les enfants comprennent rapidement que l’inconnue (le «nombre pensé») pose problème pour « refaire le calcul à l’envers » comme ils l’ont d’abord suggéré.
Manipulation de l’algorithme donné et écriture des calculs

Par groupes de travail, on manipule l’algorithme donné. Chaque élève choisit un nombre pensé, fait ses calculs. Le groupe valide le résultat.
Si les étapes de calcul sont plutôt bien exécutées, l’écriture des calculs est souvent incorrecte.
Nous travaillons notamment sur le sens du signe «égal» qui n’est pas toujours utilisé à bon escient. Collectivement, nous vérifions les calculs, nous récrivons correctement les opérations.
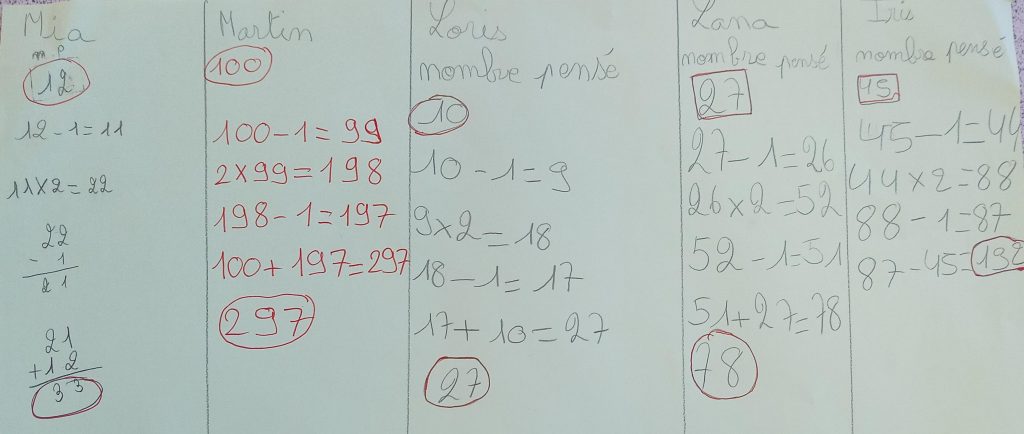
Nous nous interrogeons sur la possibilité d’écrire tous les calculs à la suite, en une seule égalité. L’idée d’utiliser des parenthèses émerge chez les enfants, « comme dans les décompositions de nombres ». Nous récrivons les calculs, en prêtant attention à l’ordre des opérations, aux parenthèses, à l’utilisation du signe « = ».
Retrouver le nombre pensé
Travail préalable en calcul mental
Afin qu’ils puissent découvrir comment retrouver le nombre pensé, les élèves sont entraînés à des procédures de calcul mental. L’objectif est d’aborder les notions de commutativité et d’associativité, et l’idée qu’un même calcul peut s’écrire de différentes manières, afin de préparer la compréhension des calculs à venir dans la séance suivante.
Un travail de recherche est proposé : Qu’est-ce qui peut faire \(50\) ?

Nous observons notamment que \({10}\times{5}={5}\times{10}\) et que \({27}+{23}={23}+{27}\), mais également les opérations «inverses» (multiplication et division ; addition et soustraction), ou encore l’équivalence entre additions itérées et multiplication.
D’autres calculs sont proposés aux enfants : ils doivent trouver des calculs équivalents. Leurs propositions sont à nouveau rassemblées au tableau.
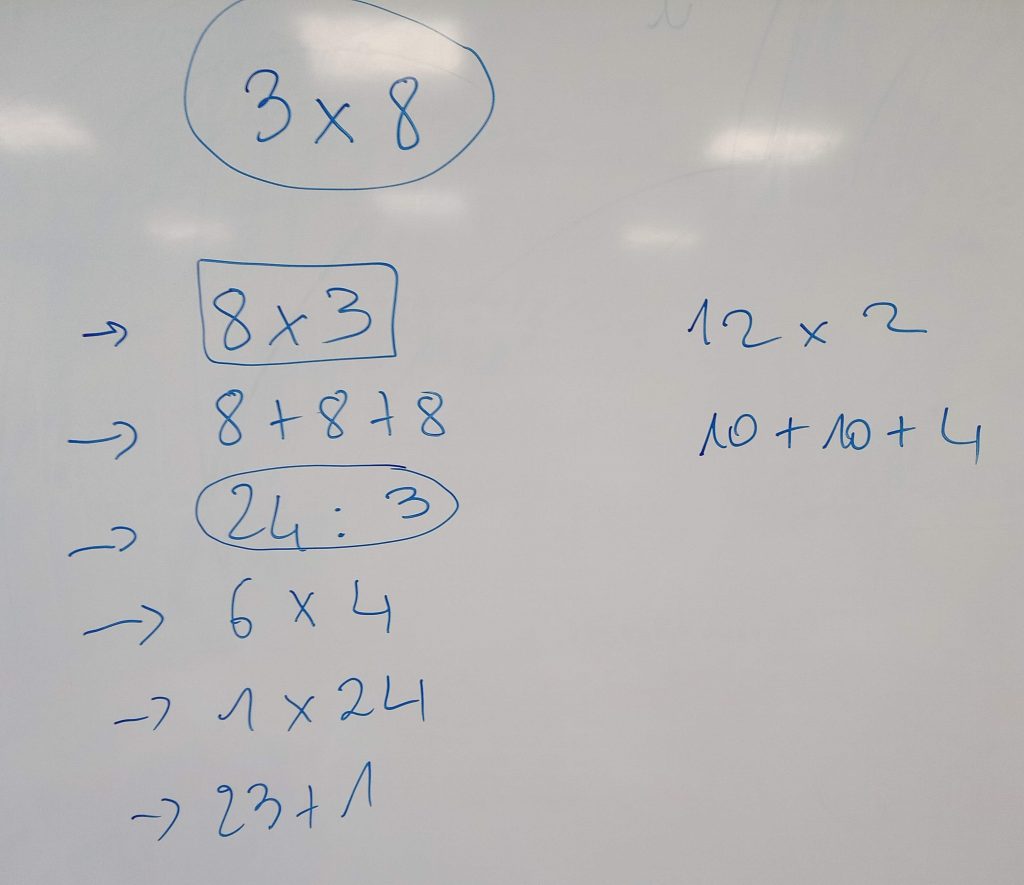

Recherche de l’astuce du magicien
Retour au tour de magie…
Chaque élève pense à nouveau à un nombre, et écrit ses calculs pour trouver son résultat. Le groupe valide. On regroupe au tableau les nombres pensés, les instructions de calcul, les résultats. On efface les instructions. On observe les calculs.
Réflexion collective : que peut-on observer ? Quels calculs se répètent ? Peut-on les remplacer par un autre calcul ? les réécrire d’une autre façon ? changer les instructions de calcul ?
Par exemple :
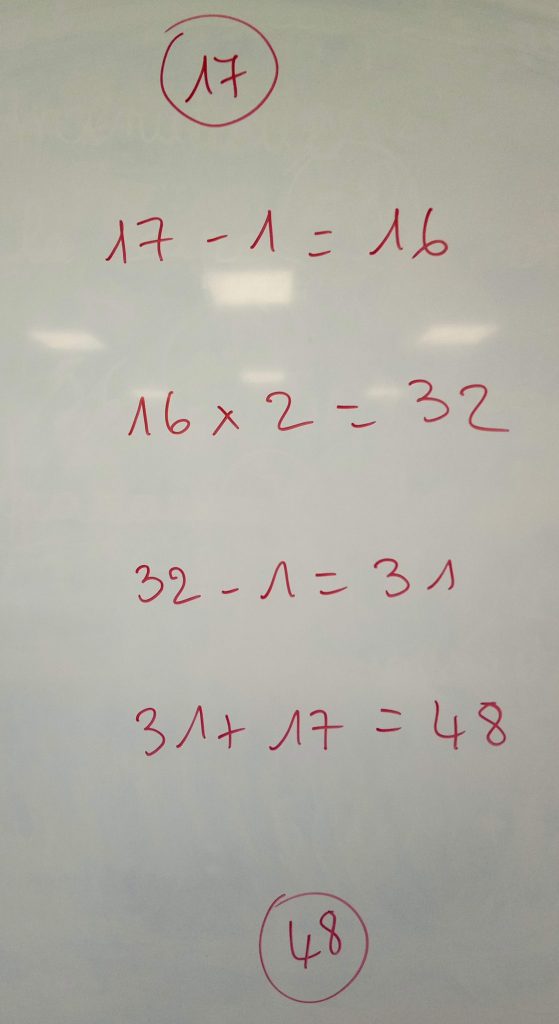
Le calcul de base (\(17-1\)) apparaît ; en décomposant tous les calculs : \[\begin{aligned}
&17-1\\
&(17-1)+(17-1)\\
&(17-1)+(17-1)-1\\
&(17-1)+(17-1)-1+17\end{aligned}\]
Enfin, nous modélisons le calcul qui permet d’obtenir le résultat à partir du nombre pensé.
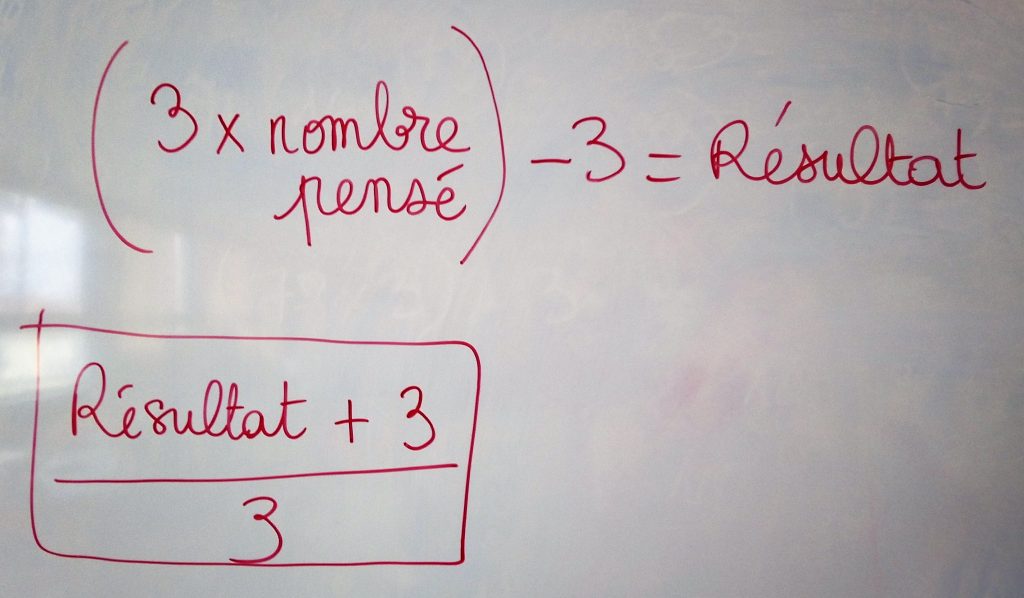
En réactivant les notions travaillées, on parvient à faire la démarche inverse : trouver le nombre pensé à partir du résultat.
On teste la formule trouvée : j’ajoute trois, je divise par trois. Les élèves jouent par deux.
Nous profitons aussi d’avoir une visite dans la classe pour tester notre tour de magie. Nous lançons le défi aux enfants : trouver le nombre pensé de notre invitée.
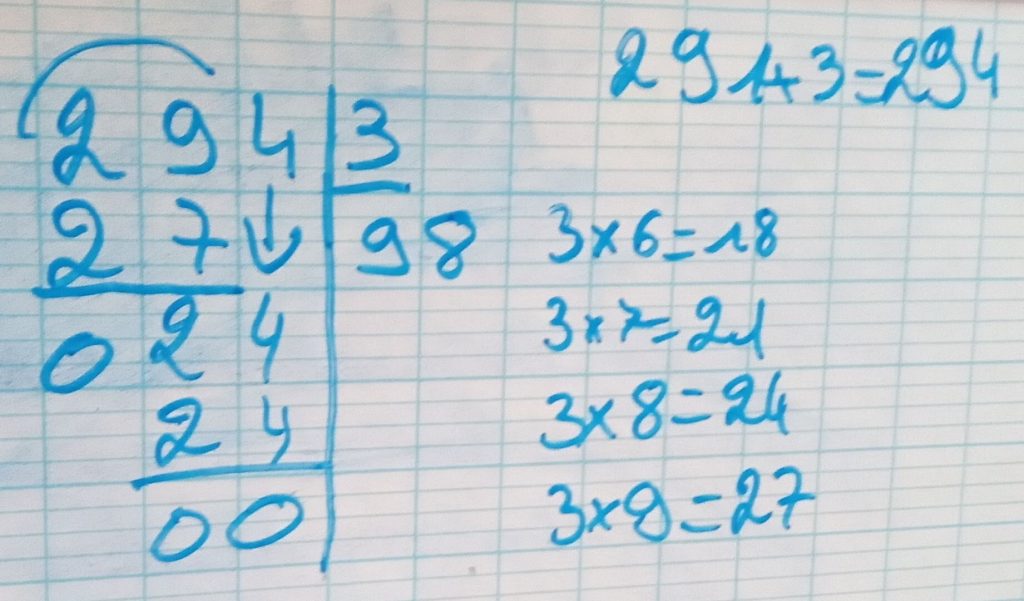
L’évaluation montre que les enfants se sont très bien appropriés les calculs. 100 % de réussite !
De nouveaux tours de magie
Maintenant que les enfants maîtrisent bien les calculs, nous leur proposons de nouveaux défis et leur demandons comment retrouver l’algorithme permettant de découvrir le nombre pensé.
| Situation n° 1 |
|---|
|
Cette situation est proposée comme travail de recherche à la maison.
La plupart des enfants n’ont pas trouvé et n’ont pas utilisé la méthode utilisée en classe, que nous reprenons ensemble. Nous réécrivons les calculs correspondants aux consignes de l’énoncé. Les enfants retrouvent ensuite le résultat «\(\text{nombre pensé}+3\)» puis l’opération inverse pour trouver le nombre pensé «\(\text{résultat}-3\)».
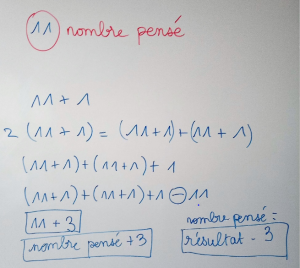
Pour que les enfants acquièrent des automatismes, il faudra encore manipuler calculs et écritures dans un grand nombre de situations similaires.
Lors des situations suivantes, nous renouvellerons la même procédure de travail : trouver l’algorithme pour retrouver le nombre pensé, tester l’algorithme par jeu de duos, manipuler à nouveau dans diverses situations.
| Situation n° 2 |
|---|
|
L’écriture des différentes étapes est retrouvée, avec ou sans parenthèses.

Les enfants parviennent à trouver une formule traduisant l’algorithme, ils identifient l’inconnue : «le nombre pensé» ou «NP», puis vérifient la formule trouvée en essayant avec d’autres nombres.

| Situation n° 3 |
|---|
|
Même déroulement… pour arriver à «\(\text{Résultat}-3=\text{nombre pensé}\)».
Un dernier tour et conclusion
| Situation d’évaluation |
|---|
|
|
Par exemple : \[\begin{aligned} |
Globalement, les élèves réinvestissent ce qui a déjà été travaillé et trouvent une solution (à noter dans les productions ci-dessous la malheureuse absence de parenthèses…).


Pour réutiliser toutes les compétences acquises durant cette séquence, on pourrait faire présenter le tour de magie à une autre classe. Après l’effet de surprise, il faudrait expliquer le tour, verbaliser, procéder par étapes, répondre aux questions.
Les enfants ont acquis de nombreuses compétences mathématiques lors de cette séquence, ils ont aussi appris à réfléchir, à chercher, à se tromper, à coopérer. Ils ont appris la rigueur. Ils ont surtout pris plaisir à relever le défi, à surmonter les difficultés, et enfin à réussir. Ils ont vécu les mathématiques comme une expérience positive, qu’ils ont partagée entre eux à l’école et avec leurs proches en dehors. «Que les nombres soient nos amis» disait le rapport Torossian-Villani : c’est ainsi, par la curiosité éveillée, par le plaisir du jeu, par le bonheur d’avoir réussi, que nous espérons avoir ouvert une porte derrière laquelle nos élèves ne resteront pas interdits.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Sarah Leleu Maati et Mathilde Scandolari sont enseignantes à l’école élémentaire Albert Camus d’Épinay-sur-Orge (91).


Une réflexion sur « Un tour de magie en CM2 »
Les commentaires sont fermés.