Des patterns dans les classes !

Avez-vous déjà entendu parler de patterns ?
Les activités de patterns présentées dans cet article sont le fruit d’une collaboration entre des chercheurs et des enseignants de collèges et d’écoles primaires au sein de la recherche PREMaTT¹. Les auteures interrogent leurs potentialités mathématiques. À (re-)découvrir et à tester dans vos classes dès le cycle 3 !

Claire Piolti-Lamorthe, Sophie Roubin, Jana Trgalová & les membres du groupe PAREP²

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

© APMEP Mars 2023

Qu’est-ce qu’un pattern ?

Peu utilisés dans les classes françaises, les patterns sont cependant des objets classiques dans de nombreux curriculums étrangers. Par exemple, dans les programmes canadiens, un des thèmes se nomme « Patterns et relations ». Il décrit sur l’ensemble de la scolarité leur utilisation pour développer le sens des nombres, la pensée algébrique, ou l’approche des fonctions. Ils se présentent sous la forme de séries de nombres ou de figures. [1]

Nous retenons comme définition pour un pattern: « Un ensemble de nombres ou d’objets dont tous les éléments sont reliés les uns aux autres par une règle spécifique. »

Nous avons choisi par ailleurs de nommer motif « un élément qui, conjugué avec une règle, va permettre de générer la série de nombres ou de figures ». Dans les pays anglo-saxons, un vocabulaire spécifique (tableau 1) permet de distinguer les activités dans lesquelles le motif se répète à l’identique (repeating pattern) et celles dans lesquelles le motif est modifié à chaque étape (growing pattern). Nous avons choisi de les traduire par pattern répétitif et pattern évolutif.

	Pattern évolutif	Pattern répétitif
Figuratif
De nombres	3— 6 — 9 — 12 8 — 17 — 26 —35 1 — 4 — 9 — 16	183 183 183
Potentialités	Vers la pensée algébrique	Vers la pensée algorithmique

Tableau 1. Classement des différents types de patterns.

Comment utiliser les patterns dans nos classes ?

Les activités de patterns peuvent être proposées à tous les cycles du primaire et du secondaire.

Différentes tâches sont communes à tous les types de séries et à tous les cycles. Les élèves vont chercher à repérer une régularité (compétences chercher et modéliser), puis la décrire en indiquant le motif et la règle associée à l’aide du langage naturel, d’un schéma ou du langage mathématique (compétence représenter).

Plusieurs consignes peuvent engager un travail autour des séries: l’ajout de nouveaux éléments, le calcul d’un élément plus ou moins éloigné, la question de l’appartenance d’un élément donné à la série. On peut aussi demander à l’élève de traduire sa régularité en créant une nouvelle série qui utilise des sons, des actions, des manipulations, des diagrammes, des tableaux de valeurs.

Par ailleurs, pour être porteuses de potentiels d’apprentissage, les activités de patterns doivent être proposées régulièrement, dans un format court, en explorant un pattern à la fois et en veillant à leur variété (figuratifs ou numériques). Elles peuvent donc être mises en place lors des moments de Mises En Train [3] et être l’occasion pour les élèves d’un temps de recherche individuel (puis éventuellement en groupe) qui sera suivi d’un partage des pistes de solutions en groupe classe avec des échanges autour des procédures et une institutionnalisation en fin d’activité, qui peut être orale ou écrite, mais qui est systématique.

Dans la suite de l’article, nous présentons des situations³ qui ont été expérimentées dans des classes du CE2 à la Troisième. Elles ont été mises en œuvre en plusieurs problèmes liés et organisés dans une progression de Mises En Train. Elles ont aussi pris la forme de défis inter-classes.

Nous mettons en parallèle plusieurs types de présentation des patterns pour montrer leurs potentialités communes⁴. Nous proposons plusieurs consignes qui établissent des contraintes stables qui font varier l’activité des élèves et permettent de développer la créativité mathématique, la pensée algorithmique et la pensée algébrique.

Développer la créativité mathématique avec des patterns

Qu’est-ce que la créativité mathématique ?

La créativité est une capacité de plus en plus demandée dans la société et dans le monde professionnel pour relever les défis économiques actuels et futurs. Elle fait partie de ce que l’on nomme les soft skills, les compétences douces, compétences comportementales, de même que la résolution de problèmes, la motivation, la confiance ou la curiosité. De ce fait, plutôt que de considérer une créativité avec un « grand C », activité exceptionnelle de certains individus talentueux mais rares (« génies »), nous postulons que toutes les personnes ont un potentiel de créativité qui peut s’exprimer dans diverses situations de la vie quotidienne. Nous considérons alors la créativité avec un « petit c », ou créativité de tous les jours, qui se produit par exemple quand une personne appréhende d’une nouvelle façon un problème. Dans le cas des mathématiques, la créativité peut être définie comme une activité intellectuelle conduisant à l’élaboration de nouvelles idées, approches ou réponses dans la résolution d’un problème mathématique [5].

Cette activité est caractérisée par quatre composantes  [6]:

• la fluidité, c’est-à-dire la capacité à générer de nombreuses idées ou réponses à un problème ;

• la flexibilité, c’est à dire la capacité à aborder le problème sous différents angles ;

• l’originalité, c’est-à-dire la capacité à produire des idées/réponses inattendues ;

• l’élaboration, c’est-à-dire la capacité d’approfondir les idées ou de redéfinir la situation initiale pour en créer de nouvelles.

L’éducation joue un rôle important pour favoriser la créativité. Mais comment un enseignant de mathématiques peut-il favoriser le développement de la créativité chez ses élèves ? Quelles expériences d’apprentissage peuvent aider les élèves à enrichir leur potentiel créatif ?

Apport des patterns

La première phase de questionnement, éventuellement vécue pour elle-même, est propice au développement de la créativité. Quelques éléments de la série sont donnés et on demande aux élèves de proposer plusieurs façons de compléter cette série. Il s’agit, pour les élèves, de dessiner le rang suivant et chercher une relation. Ils sont libres d’explorer différentes procédures de construction qu’ils doivent exprimer, sans contrainte concernant le registre et sans demande de formalisme. Plusieurs régularités différentes peuvent alors être verbalisées dans la classe et faire l’objet d’une argumentation pour convaincre de leur validité. Les élèves sont amenés à étudier une grande variété de structures à partir des mêmes éléments du pattern. Inventer, exprimer et valider ces règles de construction encourage la créativité.

Voici quelques exemples à partir d’un motif numérique et d’un motif figuratif :

Pattern de nombres	Pattern figuratif
Écrire l’élément suivant de la série en expliquant une règle qui a permis de le calculer.	Dessiner l’élément suivant de la série en expliquant une règle qui a permis de le construire.
Régularité n° 1
1 — 4 — 7 — 10 — 13 — 16 … On compte de 3 en 3 à partir de 1 (pattern évolutif)	ou
Régularité n° 2
1 — 4 — 7 — 1 — 4 — 7 — 1 — 4 — 7 … On répète les trois nombres (pattern répétitif)
Régularité n° 3
1 — 4 — 7 — 28 — 31 — 124 … On fait \(\times4\) puis \(+3\) et on continue en alternant.
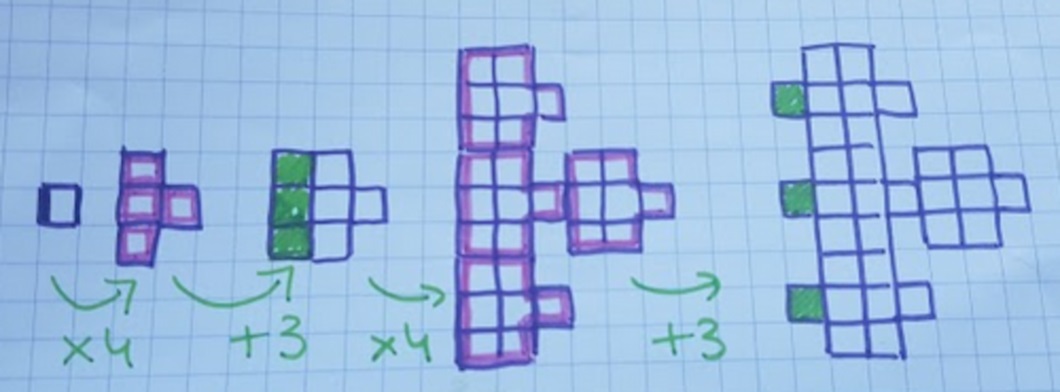Régularité n° 4
1 — 4 — 7 — 12 — 17 — 24 … On fait \( +3\) deux fois de suite puis \( +5\) deux fois de suite puis \( +7\) deux fois de suite et on continue avec tous les nombres impairs.
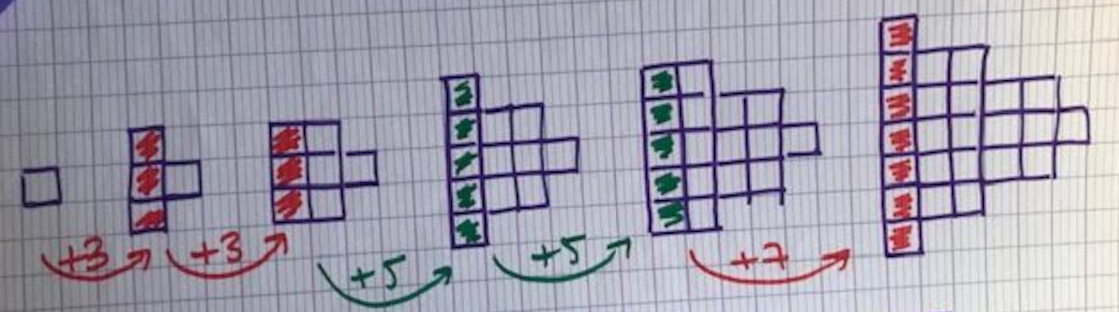Régularité n° 5
1 — 4 — 7 — 4 — 1 — 4 — 7 — 4 — 1 — 4 — 7 — 4 — 1 — 4 — 7 … C’est un pattern répétitif où les places impaires alternent 1 et 7, et où toutes les places paires contiennent un 4.

Tableau 2. Exemples de régularités exprimées par les élèves [7] .

Des variations figurées de ces patterns peuvent être faites avec des objets, dessins, mouvements, sons… Par exemple avec des cubes de couleurs un pattern suivant la régularité n° 5 ferait alterner des cubes bleus, rouges et verts (remplaçant respectivement les 1, 4 et 7).

Nous avons aussi proposé la situation en intercalant une case vide entre deux éléments : 1 — … — 7 et les élèves ont créé une plus grande variété de régularités valides, les échanges leur permettant d’être de plus en plus créatifs.
Par exemple :

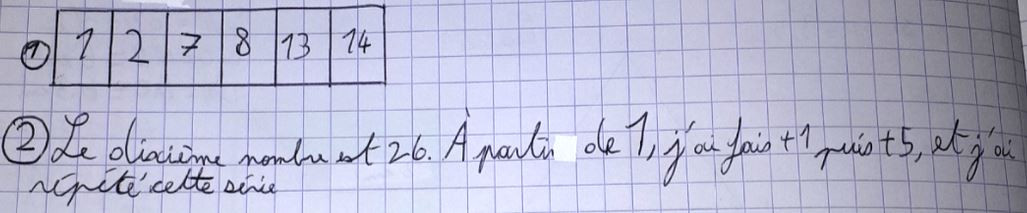
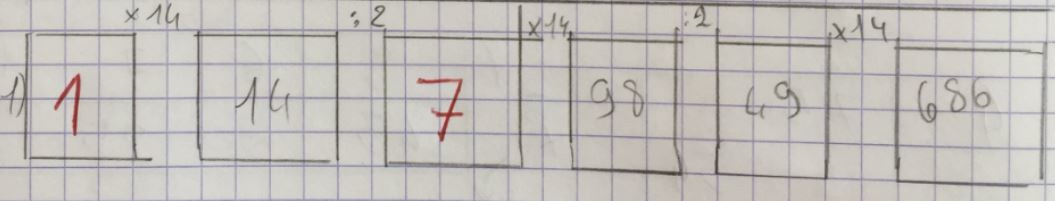
Cette pluralité de réponses à une même situation peut permettre d’éveiller la vigilance des élèves dans le domaine des fonctions par exemple : un lien fonctionnel n’est donc a priori pas unique et il faut un nombre minimum de contraintes ou d’éléments pour pouvoir le valider.

Le travail autour de la situation peut être poursuivi par d’autres questionnements qui contribueront à développer la pensée algorithmique et algébrique. Pour cela, il faudra choisir une régularité particulière à étudier.

Développer la pensée algorithmique avec des patterns

Qu’est-ce que la pensée algorithmique ?

La pensée algorithmique, appelée parfois aussi pensée computationnelle, est une manière d’aborder les problèmes. Face à un problème complexe, elle conduit à structurer les actions pour développer des solutions possibles. Ces solutions peuvent ensuite être présentées d’une manière compréhensible pour un ordinateur, un humain ou les deux . La pensée algorithmique comporte quatre composantes principales :

• décomposition ;

• reconnaissance de pattern ;

• abstraction ;

• algorithmes.

La pensée algorithmique consiste donc à prendre un problème complexe et à le décomposer en une série de petits problèmes plus gérables (décomposition). Chacun de ces petits problèmes peut ensuite être examiné individuellement, en faisant référence à des problèmes similaires déjà résolus précédemment (reconnaissance) et en se concentrant uniquement sur les détails importants, tout en ignorant les informations non pertinentes (abstraction). Ensuite, des étapes simples ou des règles pour résoudre chacun des petits problèmes peuvent être conçues (algorithmes). Enfin, ces étapes ou règles simples sont utilisées pour programmer un ordinateur afin d’aider à résoudre au mieux le problème complexe .

Apport des patterns

Sur le plan de la pensée algorithmique, les activités de patterns mettent en jeu la reconnaissance de motifs, leur description conduisant à leur généralisation (abstraction à différents niveaux).
Voici deux exemples.

Dans la figure 7, on reconnaît des carrés dont les arêtes sont de couleurs différentes, on passe d’un carré à l’autre en agrandissant la longueur du côté, l’alternance de couleurs restant la même (reconnaissance de pattern). Pour construire ce pattern, il suffit de savoir tracer un segment, tourner de 90°, changer la couleur du stylo, déplacer le stylo sans écrire et agrandir un segment (décomposition). Programmer demande de traduire ces relations fonctionnelles et logiques en algorithmes.

Dans la figure 8, on reconnaît les mêmes éléments que dans la figure 7, mais dans un autre ordre. Il est simple de modifier le script du premier pattern pour obtenir le second.

Revenons au cas du pattern de nombres évolutif obtenu avec 1 comme premier élément et la régularité n° 1 (tableau 1) et cherchons le dixième élément de cette série. Il suffit de compléter la série :

1 — 4 — 7 — 10 — 13 — 16 — 19 — 22 — 25 — 28 !

Demander un élément encore plus éloigné permet de mettre en défaut les procédures de type récurrence qui deviennent trop coûteuses en temps. Pour déterminer le centième élément, une variété des procédures de calcul des éléments peut apparaître pour une même régularité suivant la manière dont les élèves déconstruisent / décomposent le « motif ». Elles sont explicitées sous forme de schémas et en langage naturel, puis sous forme d’expressions numériques ou littérales pour les élèves du cycle 4 (figure 9).

Tant que l’élève calcule les éléments de proche en proche ou mobilise la procédure de calcul avec pour objectif de programmer une machine qui déterminera les éléments, on reste dans la pensée algorithmique.

Différentes stratégies de calcul émergent pour l’élément 100 et le mode de calcul général.

• La déconstruction du pattern figuratif pour faire apparaître la régularité.

• Un calcul de proche en proche en utilisant implicitement la proportionnalité des accroissements : quand on augmente d’un rang la série augmente de 3 ; donc pour 10 rangs on augmente de 30 et pour 90 rangs de 270…

• La recherche d’un programme de calcul (lien fonctionnel) reliant le rang et l’élément par tâtonnement, ou en utilisant les multiples de \(3\), ou encore en ayant recours à la division euclidienne à partir de l’information \({}+3\).

  On obtient ainsi différentes formulations :

  \(\mathbf{1}\times3-2\), \(\mathbf{2}\times3-2\), \(\mathbf{3}\times3-2\), …

  ce qui permet aux élèves de généraliser ce mode de calcul jusqu’à 100 ou de verbaliser en langage naturel « on multiplie le rang par \(3\) et on enlève \(2\) » puis au cycle 4 en langage algébrique, « j’appelle \(n\) le rang, \(n\times3-2\) ».

  \(\mathbf{0}\times3+1\), \(\mathbf{1}\times3+1\), \(\mathbf{2}\times3+1\), …

  ou « additionner \(1\) et \(3\) fois le numéro de l’étape d’avant », « j’appelle \(n\) le rang, \(1+(n-1)\times3\) ». Cette expression est plus difficile à exprimer en langage algébrique car les élèves utilisent souvent une autre lettre pour le rang précédent.

Lorsque l’on s’interroge sur l’équivalence des différentes expressions ou qu’on mobilise le programme pour retrouver un multiple de 3, on entre dans la pensée algébrique.

Développer la pensée algébrique avec des patterns

Qu’est-ce que la pensée algébrique ?

D’après Kieran [8, p. 149], la pensée algébrique dans les premières années implique le développement de modes de pensée au sein d’activités pour lesquelles l’algèbre symbolique des lettres peut être utilisée comme outil, mais qui ne sont pas exclusives à l’algèbre et dans lesquelles on pourrait s’engager sans utiliser aucune algèbre symbolique des lettres. Il propose des exemples de ce type d’activités : analyser des relations entre les quantités, reconnaître une structure, étudier une évolution, généraliser, modéliser, justifier, prouver ou encore prédire.

Plus récemment, Radford [9] définit trois caractéristiques spécifiques de la pensée algébrique :

• l’indétermination : capacité à exploiter les problèmes qui impliquent des nombres inconnus ;

• la dénotation : capacité à nommer ou symboliser ces nombres inconnus de différentes manières (à l’aide du code alphanumérique, mais aussi du langage naturel, de gestes ou de signes non conventionnels) ;

• le raisonnement analytique : capacité à opérer sur ces nombres indéterminés comme s’ils étaient connus.

Ce que nous retenons de ces définitions c’est que des activités de patterns permettent de développer la pensée algébrique en mettant en jeu la reconnaissance de la structure du pattern (relation à propos des quantités ou des nombres), la nécessité d’exprimer une règle qui permet d’anticiper les éléments éloignés du pattern (généralisation) et de la vérifier et justifier [1].

Apport des patterns

Dans des activités patterns, les élèves développent des idées algébriques quand ils construisent ou identifient des patterns numériques ou géométriques, décrivent verbalement des patterns et les représentent à l’aide de tableaux ou symboles, cherchent et appliquent des relations entre des quantités qui varient pour faire des prédictions, élaborent des généralisations (ou règles) et les vérifient, utilisent des graphes pour décrire des patterns et faire des prévisions, ainsi que pour explorer des propriétés numériques [10, p.9].

Pour recourir à la pensée algébrique, on peut poser le type de questions suivantes.

Trouver un moyen de calculer n’importe quel élément de la série.

Par exemple, dans le cas de la spirale du pattern de la figure 8, le recours à la pensée algébrique permet, sans tout tracer, de trouver la couleur de n’importe quel élément et de continuer la suite autant que l’on veut. C’est un fonctionnement différent de celui de la pensée algorithmique qui permet de trouver une suite d’actions (algorithme) qui permettrait d’atteindre aussi un élément éloigné, mais nécessiterait de le faire en passant par tous les éléments précédents et à l’aide d’une machine.

… est-il un élément de la série ?

Par exemple, dans le cas du pattern évolutif obtenu avec 1 comme premier élément et la régularité (tableau 1) on peut se poser les questions suivantes : \(96\) appartient-il à la série ? \(598\) appartient-il à la série ?

Tous les éléments de la série peuvent être vus comme une table de \(3\) décalée de \(1\) ou de \(2\). En effet, si on soustrait \(1\) ou si on ajoute \(2\) à chaque élément de la série, on obtient les multiples de \(3\).

Si un nombre est dans cette série, il est possible pour les élèves d’en dire :

• ce n’est pas un multiple de \(3\) ;

• si je lui enlève \(1\) alors le résultat est dans la table de \(3\) ;

• si je lui ajoute \(2\) alors le résultat est dans la table de \(3\) ;

• le reste de la division euclidienne de ce nombre par \(3\) est \(1\) ;

• si j’ajoute à ce nombre un multiple de \(3\) alors le résultat sera lui aussi un élément de la série.

Les élèves sont capables de décrire comment on atteint un élément avec la pensée algorithmique, mais il ne sont pas en capacité de décrire chaque élément de la série, alors qu’ils le peuvent avec la pensée algébrique.

Par exemple, pour la question « \(598\) appartient-il à la série ? » :

Procédures algorithmiques

à partir d’un élément déjà calculé, par exemple le centième élément qui est \(298\). Pour obtenir \(598\), on ajoute \(300\) à \(298\) ce qui correspond à cent pas ; se demander si l’écart entre \(598\) et \(1\) est parcouru en faisant un nombre entier de fois \(+3\) ; …

Procédures algébriques

se demander si « \(598-1\) ou \(598+2\) sont-ils des multiples de \(3\) ? » en mobilisant par exemple le critère de divisibilité par \(3\) ; « la division de \(598\) par \(3\) admet-elle bien un reste égal à \(1\) ? » ; …

En synthèse, quelques points de vigilance

Les activités autour des patterns nous semblent porteuses de potentiels, en lien avec nos programmes de mathématiques actuels. Elles semblent propices au développement de la créativité, de la pensée algorithmique et de la pensée algébrique.

Les phases classiques de questionnement d’une activité de patterns sont les suivantes :

• Consigne n° 1 : écrire (dessiner) l’élément suivant de la série en expliquant une règle qui a permis de le calculer (construire).

Pour aller vers les tâches des consignes suivantes, il faut faire avec la classe, un choix de régularité. On veillera à varier les types de régularité pour encourager la créativité des élèves et travailler différentes notions du programme.

• Consigne n° 2 : calculer le dixième élément de la série (le calcul d’un élément proche) ;

• Consigne n° 3 : calculer le centième élément de la série (le calcul d’un élément plus éloigné).

\(10\) et \(100\) étant choisis pour questionner le recours à la proportionnalité qui pourra être discuté et invalidé en choisissant des contre-exemples dans les premiers éléments.

• Consigne n° 4 : trouve une façon de calculer n’importe quel élément de la série ;

• Consigne n° 4 bis : un élément donné appartient-il à la série ?

Lors de l’élaboration d’une progression de patterns, il semble nécessaire, pour chaque activité, de faire un choix concernant l’aspect à travailler, puis d’articuler ces activités pour en varier les aspects. En particulier, le travail sur les pensées nécessite de contraindre le choix de la règle en opposition avec le travail sur la créativité qui demande de la part de l’enseignant un certain lâcher-prise et une plus grande adaptabilité.

Pour finir, on peut noter qu’une limite de ces activités est de ne travailler que des nombres entiers (discret), il sera donc important de les associer à d’autres activités comme par exemple les programmes de calcul [11] !

Références

1. S. Coppé et al. « Un exemple de collaboration entre enseignants et chercheurs autour de la conception de ressources pour développer la pensée algébrique ». In : Dispositifs et collectifs pour la formation, l’enseignement et l’apprentissage des mathématiques (2021). Actes du 47^e colloque COPIRELEM. , p. 414-425.

2. C. Loisy et al. « Collaboration entre et avec les acteurs de terrain et effets sur les ressources et le développement professionnel. Le cas de PREMaTT ». In : Favoriser des collaborations entre chercheurs et praticiens. L’expérimentation de l’Institut Carnot de l’Éducation Auvergne-Rhône-Alpes. Sous la dir. de B. Meslin et al. Presses universitaires Blaise-Pascal, 2022, p. 197-222. 

3. S. Martin Dametto, C. Piolti-Lamorthe et S. Roubin. « TRAIN : Travail de Recherche ou d’Approfondissement avec prise d’Initiative ». In : Bulletin de l’APMEP n° 502 (janvier-février 2013). , p. 11-22.

4. « Patterns. Des problèmes pour travailler les pensées algorithmique et algébrique » In : Guide bleu « résolution de problèmes au collège ». . Éduscol. Chap.4, p. 105-128.

5. M. El-Demerdash et al. « Design and evaluation of digital resources for the development of creative mathematical thinking: a case of teaching the concept of locus ». In : Technology in Mathematics Teaching : Selected papers of the 13^th ICTMT Conference. Sous la dir. de G. Aldon et J. Trgalová. Springer, 2019, p. 145-172.

6. E.P. Torrance. « The nature of creativity as manifest in its testing ». In : The nature of creativity: contemporary psychological perspectives. Sous la dir. de R.J. Sternberg. Cambridge University Press, 1988, p. 43-75. 

7. C. Piolti-Lamorthe et S. Roubin. « Vers la pensée algébrique ». In : Les maths est-ce que ça compte ? Dossier des Cahiers pédagogiques n° 573 (2021). Sous la dir. de B. Hebben et C. Lommé. , p. 42. 

8. C. Kieran. « Algebraic thinking in the early grades: What is it? ». In : The Mathematics Educator 1. n° 8 (2004), p. 139-151.

9. L. Radford. « The progressive development of early embodied algebraic thinking ». In : Mathematics Education Research Journal n° 26 (2014), p. 257-277.

10. H. Squalli. « Introduction. Early algebra : genèse d’un domaine de recherche, évolution et perspectives ». In : Le développement de la pensée algébrique à l’école primaire et au début du secondaire. Recherches et perspectives curriculaires. Sous la dir. de H. Squalli et al. Livres en ligne, . Québec : CRIRES, 2020, p. 4-20. 

11. C. Alves et al. « Utilisation des programmes de calcul pour introduire l’algèbre au collège ». In : Repères IREM n° 92 (juillet 2013). , p. 9-30. 

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Claire Piolti-Lamorthe, présidente actuelle de l’APMEP, est professeure de mathématiques au collège Raoul-Dufy à Lyon et formatrice à l’Inspé de Lyon.
Sophie Roubin est professeure de mathématiques au collège Ampère à Lyon et chargée de mission à l’IFÉ-ÉNS de Lyon. Elle est aussi membre de la commission collège de l’APMEP.
Jana Trgalová est maîtresse de conférences en didactique des mathématiques à l’université Claude Bernard Lyon 1 et à l’Inspé de Lyon.

---

1. PREMaTT : Penser les ressources de l’enseignement des mathématiques dans un temps de transitions . Cette recherche [1, 2] a débuté dans le cadre d’un LéA-IFÉ , puis s’est poursuivie dans le cadre du projet PAREP (Pensée algébrique ressources et pratiques) soutenu par l’Institut Français de l’Éducation et l’INSPÉ de Lyon. Dans ce cadre, les auteures ont conçu collaborativement des ressources autour de questions mathématiques en lien avec la pensée algébrique.
2. Ce groupe comprend aussi les membres suivants : Cynthia Galou (professeure des écoles en CE2), Alexandra Goislard (professeure en collège et IFÉ-ÉNS de Lyon), Sandra Popov (professeure en collège), Denis Roche (professeur des écoles en CM2 et référent mathématique de circonscription).
3. Le chapitre 4 du guide La résolution de problèmes mathématiques au collège [4] explore les potentialités des patterns et complète nos propositions.
4. Il est aussi possible de proposer aux élèves du matériel pour construire les éléments du pattern.

---