Difficultés d’apprentissage en mathématiques
ou dyscalculie ?

« À l’école primaire, je n’ai pas compris pendant longtemps pourquoi \(1+1= 2\). Je pensais que cela devait être 11. »
« Je ne peux pas visualiser les quantités. Combien font 100 g ? Je n’y arrive pas dans ma tête. »
Voici deux témoignages [1] de personnes souffrant de leurs difficultés en mathématiques. Lorsque ces difficultés persistent et impactent la vie quotidienne, elles peuvent être le témoin d’un trouble des apprentissages : la dyscalculie.

Marie-Line Gardes

© APMEP Décembre 2022

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Difficulté ou trouble d’apprentissage ?

Voici des traces d’une élève de CE2, recueillies tout au long de l’année (figure 1). Chaque jour, elle devait recopier sur son cahier du jour « Rituels du matin ».

Nous pouvons constater les éléments suivants : il y a huit orthographes différentes de l’expression « Rituels du matin », les erreurs ne sont pas toujours de même nature (inversion de lettres, ajout ou oubli d’une lettre, oubli de mots, etc.), l’expression est parfois bien orthographiée. Cette rapide analyse met en évidence des difficultés en orthographe qui semblent instables et persistantes. Une analyse plus poussée des connaissances et compétences de cette élève, notamment dans les autres disciplines, montrera que ses difficultés sont spécifiques à l’apprentissage de la langue et plus particulièrement à l’orthographe. Elles sont le témoin d’une dysorthographie  [2].

Cet exemple permet de mettre en lumière la distinction entre difficulté et trouble d’apprentissage. Les difficultés sont provisoires, contextuelles (c’est-à-dire liées aux situations dans lesquelles elles se manifestent) et plurielles (leurs origines sont diverses, par exemple liées au contenu mathématique ou aux choix didactiques de l’enseignant, etc.). Le trouble, quant à lui, présente d’autres caractéristiques : il est avéré, persistant et d’origine neuro-développementale. Il doit être diagnostiqué par une équipe de professionnels et nécessite des interventions de l’ordre de l’adaptation et de la compensation  [3]. Dias [4] précise que l’intérêt de cette distinction « est essentiellement de définir des rôles différenciés des acteurs [enseignant, enseignant spécialisé, orthophoniste, thérapeute, etc.] quant à la prise en charge des élèves ».

Depuis plusieurs années, les recherches en sciences cognitives et en sciences de l’éducation s’intéressent de plus en plus à la dyscalculie, trouble spécifique des apprentissages mathématiques.

La dyscalculie dans les recherches en sciences cognitives

Les recherches en sciences cognitives définissent la dyscalculie comme un trouble spécifique de l’apprentissage qui affecte l’acquisition de compétences mathématiques en dépit d’une intelligence et d’une scolarisation normales. Les taux de prévalence de la dyscalculie varient entre 3 et 6 % des enfants d’âge scolaire (pour une synthèse, voir [5]). Cette variabilité est due à la divergence des critères utilisés pour caractériser un individu comme « dyscalculique ». Schwartz et Prado [6] avancent ainsi qu’une « meilleure caractérisation de la dyscalculie nécessiterait de tester plusieurs compétences mathématiques et leur évolution dans le temps, d’écarter l’anxiété en mathématiques comme principale source de difficulté, de vérifier la présence de comorbidité¹ et d’évaluer les capacités cognitives générales ».

Les recherches en sciences cognitives proposent également plusieurs théories pour expliquer les causes de la dyscalculie, en combinant des données comportementales et de neuro-imagerie. Décrite à l’origine comme un trouble de la compréhension des nombres et des quantités, des recherches récentes avancent que des facteurs cognitifs généraux tels que la mémoire de travail, les fonctions exécutives (par exemple, l’attention, l’inhibition ou la planification) et l’attention pourraient également être affectés dans la dyscalculie. Ainsi, la dyscalculie est très probablement un trouble hétérogène, c’est-à-dire touchant plusieurs capacités cognitives (pour une synthèse, voir [5]).

Ce champ de recherche s’intéresse donc à des questions théoriques sur la définition, la prévalence et les causes de la dyscalculie. De plus en plus d’études s’intéressent à élaborer puis évaluer des interventions permettant d’aider les enfants présentant une dyscalculie à apprendre des mathématiques. Ces recherches sont davantage menées dans un contexte de remédiation et encore très peu dans un contexte scolaire, en classe ordinaire.

La dyscalculie dans les recherches en éducation

La dyscalculie est encore peu étudiée dans le domaine de l’éducation. Comme dans les recherches en sciences cognitives, de nombreuses tentatives de définition et de terminologie ont eu lieu ces dernières années, avec toutefois une problématique spécifique à ce champ de recherche. En effet, dans le contexte scolaire, les élèves ne sont pas toujours diagnostiqués (ou le diagnostic n’est pas communiqué) et l’enseignant doit pouvoir adapter son enseignement à tous les élèves, qu’ils soient diagnostiqués ou non. Ainsi, les recherches en éducation adoptent un point de vue plus global sur les troubles d’apprentissage en mathématiques (voir la caractérisation ci-dessous, figure 2  que celui des recherches en sciences cognitives.

Figure 2. Caractérisation des troubles d’apprentissage en mathématiques dans les recherches en éducation  [7].

Dans une récente revue de littérature, Deruaz et ses collègues  [7] proposent une caractérisation des troubles d’apprentissage en mathématiques au sein de ce champ de recherche (figure 2 ) qui regroupe :

• la dyscalculie. Des enfants identifiés par un diagnostic clinique et présentant des difficultés d’apprentissage persistantes et spécifiques aux mathématiques ;

• les troubles d’apprentissage. Des enfants qui sont diagnostiqués comme ayant des troubles d’apprentissage (par exemple dyslexie, dyspraxie, etc.) qui impactent les apprentissages mathématiques mais qui ne sont pas spécifiques aux mathématiques ;

• des difficultés sévères en mathématiques. Des enfants qui n’ont pas de diagnostic mais qui présentent des difficultés d’apprentissage spécifiques aux mathématiques mais dont on ne sait pas si elles sont persistantes ou non.

Sur la base de cette catégorisation, les recherches sont peu nombreuses (dix-neuf articles dans les revues principales de recherche sur l’enseignement des mathématiques entre 2007 et 2016), relativement récentes et menées, en majorité, par des équipes américaines. Les participants à ces études sont des enfants entre 7 et 12 ans. Les études portent principalement sur des contenus mathématiques relevant de l’arithmétique élémentaire (opérations, fractions, résolution de problèmes). Une majorité de ces études cherchent à développer et tester des interventions mais peu sont réalisées au sein de la classe directement.

Les auteurs mentionnent en conclusion que les recherches doivent se poursuivre, notamment pour identifier les difficultés persistantes des élèves ayant des troubles des apprentissages en mathématiques pour ensuite proposer des interventions spécifiques et ciblées sur ces difficultés.

Identifications des difficultés de la dyscalculie

Les recherches en sciences cognitives et en éducation recensent des difficultés de natures variées chez les personnes ayant un diagnostic de dyscalculie. Nous en présentons quelques-unes ci-dessous.

Difficultés avec la quantité et la cardinalité

Les premiers signes de difficultés en mathématiques provoquées par la dyscalculie peuvent se manifester dès les premiers apprentissages mathématiques, c’est-à-dire sur la construction du nombre entier à l’école maternelle. Les enfants peuvent avoir des difficultés persistantes pour estimer, comparer des quantités, pour maîtriser la comptine orale ou encore pour dénombrer ou constituer une collection d’objets. Il est difficile pour eux de comprendre et donner du sens à la grandeur quantité d’une collection d’objets puis à la cardinalité d’un ensemble (i.e. dire combien il y a d’objets en tout).

Difficultés avec la mémorisation des faits numériques et la maîtrise des opérations

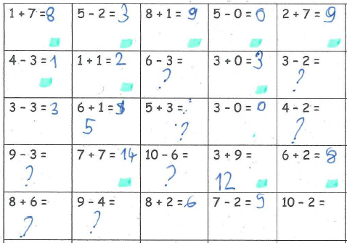
Les élèves présentant une dyscalculie peuvent avoir des difficultés pour mémoriser les faits numériques et la maîtrise des opérations. La figure 3 montre par exemple un extrait d’une production d’un élève de 9 ans dans un test de fluence en calcul. Il devait résoudre le plus possible d’opérations en trois minutes. On peut remarquer sa relative maîtrise des additions (de deux nombres à un chiffre) mais ses difficultés dans les opérations dont un opérande est 0 ou dans les soustractions.

Difficultés dans la compréhension du système de numération décimale

Les élèves ayant une dyscalculie présentent très souvent des difficultés dans la compréhension du système de numération décimale. Les tâches de transcodage, c’est-à-dire passer du nom de nombre (mot-nombre) à l’écriture chiffrée et inversement sont assez révélatrices de la mauvaise compréhension du principe positionnel. Un enfant pourrait ainsi écrire 500302 dans une dictée de nombres pour cinq-cent-trente-deux (532). Cette difficulté entraîne ensuite de nombreuses erreurs dans les algorithmes posés. La figure 4 illustre le calcul posé par un enfant de 11 ans (présentant une dyscalculie) d’une addition de trois termes, dont deux nombres décimaux et un nombre entier. Cet enfant aligne les écritures des trois nombres à droite et commet donc l’erreur de placer le nombre entier dans la colonne des centièmes, ce qui le conduit à donner la réponse 5,80). À noter qu’il n’a a priori pas de difficulté avec la retenue. Cependant, on peut se demander s’il en comprend la signification, c’est-à-dire est-ce qu’il maîtrise l’aspect décimal de la numération (10 unités}=1 dizaine)) ?

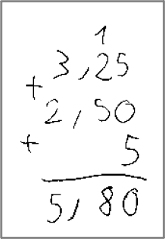
Difficultés avec les procédures de calcul et les algorithmes

La dyscalculie peut entraîner des difficultés pour effectuer tous types de calculs : calcul mental, calcul en ligne, calcul posé. Dans des calculs simples à effectuer mentalement, les élèves auront par exemple des difficultés à utiliser des procédures de surcomptage et auront besoin de recourir au recomptage ou au comptage sur les doigts plus longtemps. Dans le calcul mental et le calcul en ligne, une des difficultés principales pour les élèves est de réussir à changer de procédure en fonction du calcul à réaliser. Il s’agit d’utiliser une forme de flexibilité cognitive, en appui sur des connaissances mathématiques, pour choisir une procédure efficace et pertinente et échapper ainsi à une forme de « rigidité arithmétique » [8].

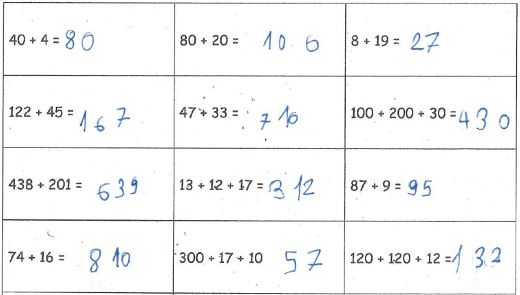
La figure 5 illustre les difficultés d’un élève de 9 ans, liées à une mauvaise compréhension du principe décimal de la numération. Pour plusieurs calculs, il calcule le nombre d’unités puis le nombre de dizaines et les accole. Il ne procède pas aux échanges de \(10\) unités en une dizaine. Pour les calculs \(80+20\) ; \(122+45\) ; \(438+201\), cette procédure donne le bon résultat car il n’y a pas de franchissement de dizaine ; en revanche, pour \(47+33\) ; \(74+16\) ; \(13+12+17\), sa procédure produit des erreurs, il juxtapose le nombre de dizaines avec le nombre d’unités. Ainsi pour \(47+33\), il faudrait lire \(7\) \(10\) comme \(7\) dizaines et \(10\) unités (ce qui est correct), pour \(74+16\), il faudrait lire \(8\) dizaines et \(10\) unités et pour \(13+12+17\),  \(3\) dizaines et \(12\) unités.

Difficultés dans la compréhension des nombres rationnels

L’apprentissage des nombres rationnels est particulièrement connu pour être difficile chez tous les élèves. Pour ceux qui présentent une dyscalculie, la comparaison de fractions, l’estimation de la grandeur d’une fraction, l’utilisation des procédures de calculs (pour additionner ou multiplier deux fractions), le placement et le repérage d’une fraction sur une droite graduée et la résolution de problèmes avec des fractions sont particulièrement des points sensibles et persistants. Dans une récente étude [9], nous avons mis en évidence ces difficultés persistantes en les identifiant spécifiquement chez des adultes présentant une dyscalculie (c’est-à-dire que nous n’avons pas identifié ces difficultés dans les réponses des adultes sans dyscalculie). Nous en présentons quelques-unes ci-dessous.

Dans les tâches de placement et repérage d’une fraction sur une droite graduée, les erreurs révèlent une difficulté à comprendre la notion d’unité (figures 6 et 7).

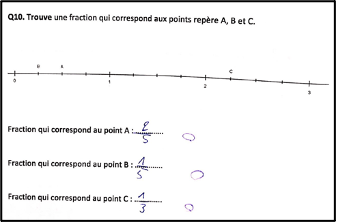
Par exemple, sur cet extrait (figure 6), cet adulte a compté les graduations au lieu de compter le nombre d’intervalles entre les graduations pour déterminer le dénominateur. Sur la droite numérique coupée en quarts, cela l’a conduit à exprimer des fractions en cinquièmes.

Et sur cet extrait (figure 7), le participant a découpé la droite numérique (allant de \(0\) à \(3\)) en douze parties et a marqué le point B comme \(\dfrac{1}{12}\cdotp\) Cela indique qu’il a mal identifié l’unité : il a pensé que la droite entière représentait une unité alors qu’elle en représente trois.

Dans les procédures de calcul, une erreur récurrente est la prise en compte du numérateur uniquement. Par exemple, pour décomposer \(\dfrac{7}{5}\) (figure 8), le participant a décomposé le numérateur \(7\) en \(2\) et \(5\), sans tenir compte du rôle du dénominateur et répond \(\dfrac{7}{5}=2+\dfrac{\mathstrut5}{5}\cdotp\) Dans l’ajout d’un nombre entier à une fraction, il a ajouté le nombre entier au numérateur, par exemple, \(4+\dfrac{1}{2}=\dfrac{5}{2}\) (figure 8).

Figure 8. Production d’un adulte dyscalculique sur une tâche de décomposition. Source : [9].

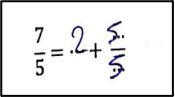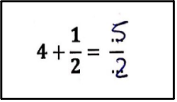Une autre erreur récurrente est l’ajout des numérateurs et des dénominateurs séparément dans des additions de deux fractions. Ce qui est spécifique, chez les adultes dyscalculiques, c’est qu’ils utilisent cette procédure, aussi bien avec des dénominateurs semblables qu’avec dénominateurs différents (figure 9).

Pour conclure sur l’identification des difficultés liées à la dyscalculie, nous pouvons avancer, avec un regard didactique, que ces difficultés ne semblent pas spécifiques à ces élèves, ce sont en effet des difficultés « classiques » du début des apprentissages sur la quantité, le nombre entier, le système décimal, les fractions, etc. Ce qui caractérise donc ces difficultés est plutôt leur caractère persistant dans le temps et instable.

Ceci implique, pour l’enseignant, un travail minutieux d’identification des difficultés afin de pouvoir remédier le plus efficacement possible, c’est-à-dire en ciblant précisément ces difficultés.

Que faire pour aider les élèves présentant une dyscalculie ?

Comme mentionné plus haut, à l’heure actuelle, les recherches ont davantage eu des impacts et des retombées sociétales auprès des professionnels spécialistes de la remédiation (orthophoniste, neuropsychologue) en proposant des outils pour diagnostiquer et des propositions d’intervention (voir des exemples dans [5]). Du côté de la classe ordinaire à visée inclusive, les enseignants ordinaires et spécialisés se trouvent fort démunis. Des ressources arrivent petit à petit, on peut par exemple citer un livre récent co-écrit par une professeure des écoles et une médecin en rééducation [10] ou encore le document de la Conférence Intercantonale de l’Instruction Publique de la Suisse romande et du Tessin [8].

Les recherches en didactique des mathématiques ne se sont pas encore réellement emparées des questions spécifiques posées par les troubles des apprentissages et plus spécifiquement de la dyscalculie. Pourtant, la vision systémique sur les difficultés d’apprentissage que porte la didactique [11] en questionnant, outre le point de vue de l’élève, le contexte, les caractéristiques de la situation, l’enseignement proposé, etc., permettrait d’apporter des outils pertinents pour répondre à la délicate question de l’articulation de l’identification des difficultés et des interventions associées[12].

Voici un exemple qui illustre l’apport d’une analyse didactique pour identifier puis élaborer une remédiation pertinente face à une difficulté spécifique en mathématiques. Prenons l’apprentissage du dénombrement à l’école maternelle et un enfant qui ne parvient pas à dire combien d’éléments a une collection. Pour comprendre la difficulté sous-jacente, il est nécessaire d’observer la procédure mise en place par l’élève, les erreurs commises, voire de le questionner sur ses actions. Si l’erreur provient d’un problème de synchronisation entre le geste de pointage et le nom du nombre (mot-nombre) de la comptine énoncée ou si l’erreur provient d’erreurs dans la comptine numérique, la tâche est échouée pour des raisons différentes et doit donc appeler à des remédiations différentes. En effet, dans le premier cas, il s’agit d’une difficulté liée à la maîtrise de l’énumération, et dans le second cas, il s’agit d’une difficulté dans la maîtrise de la comptine numérique. Dans le premier cas, on pourrait proposer une intervention visant à travailler l’énumération et le geste de pointage, notamment en jouant sur certaines valeurs de variables didactiques (taille de la collection, type d’organisation des éléments de la collection — linéaire, circulaire, aléatoire —, possibilité de marquage, etc.). Dans le second cas, il faudra travailler la comptine numérique et ses niveaux de maîtrise [13], par exemple avec différentes comptines et des rituels (furet de \(1\) en \(1\), fusée, etc.).

Ainsi la perspective didactique sur les troubles des apprentissages suggère de renforcer les connaissances et compétences mathématiques et didactiques de l’enseignant et de proposer des outils pour qu’ils puissent concevoir des situations d’enseignement pertinentes, analyser finement les erreurs des élèves, identifier leurs difficultés et élaborer des interventions de remédiation liées aux difficultés repérées.

Pour conclure, les recherches doivent se poursuivre, la formation des enseignants en didactique des mathématiques s’intensifier… et les enseignants se faire confiance sur leurs analyses mathématiques et didactiques pour imaginer et proposer des interventions pertinentes et cohérentes au regard des difficultés identifiées chez leurs élèves, qu’ils soient diagnostiqués ou non !

Références

1. K. Landerl. Dyscalculia – the neglected learning disorder.. University of Graz, 2019.
2. Inserm. Dyslexie, dysorthographie, dyscalculie : bilan des données scientifiques.. 2007.
3. T. Dias. Enseigner les mathématiques à l’école. Une démarche positive pour des apprentissages réussis. Magnard, 2018.
4. T. Dias. « Difficultés d’apprentissage en mathématiques : un regard didactique ». In : J. Pilet et C. Vendeira. Actes du séminaire national de didactique des mathématiques de l’ARDM. . Mars 2018, p. 251- 259.
5. M.-P. Noël et G. Karagiannakis. Dyscalculie et difficultés d’apprentissage en mathématiques : guide pratique de prise en charge. De Boeck Supérieur, 2020.
6. F. Schwartz et J. Prado. « La dyscalculie développementale : bases cérébrales et cognitives. » In : J. Pilet et C. Vendeira. Actes du séminaire national de didactique des mathématiques de l’ARDM.. Mars 2018, p. 232-250.
7. M. Deruaz et al. « Exploring MLD in mathematics education : Ten years of research ». In : The Journal of Mathematical Behavior n ° 60 (2020). , p. 1-17.
8. Conférence intercantonale de l’instruction publique de la Suisse romande et du Tessin (CIIP). « Dyscalculie (trouble spécifique d’apprentissage en mathématiques) à l’école régulière. Informations à l’intention des enseignant · e · s sur le trouble, les mesures de différenciation pédagogique et la compensation des désavantages ». In : (2020). .
9. M.-L. Gardes. « Compréhensions des fractions chez des adultes porteurs ou non de dyscalculie développementale ». In : La cognition mathématique. État des pratiques et de la recherche (2021). Sous la dir. de G. Hilaire-Debove et N. Joyeux, p. 265-284.
10. G. Loty et M. Mazeau. DYS : outils & adaptations dans ma classe. Retz, 2020.
11. J. Giroux. « Difficultés des élèves en mathématiques au primaire : les apports de la didactique ». In : Math-École n° 224 (2013), p. 4-7.
12. F. Peteers. « Apports croisés de la didactique et de la cognition numérique pour l’étude des troubles des apprentissages en mathématiques ». In : Recherches En Didactique Des Mathématiques n °40 (2) (2020). p. 225-268.
13. K. Fuson. « Relation entre comptage et cardinalité chez les enfants de 2 à 8 ans ». In : Les chemins du nombre. Sous la dir. de J. Bideaud, C. Meljac et J-P. Fischer. Lille : Presses universitaires de Lille, 1991, p. 158-182.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Marie-Line Gardes est professeure à la HEP Vaud à Lausanne en didactique des mathématiques. Ses travaux de recherche portent notamment sur les troubles et les difficultés d’apprentissage en mathématiques.