Petite enquête sur … la modélisation
Complément numérique
François Boucher
© APMEP Mars 2022
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
De quoi est-il question ?
Dans cette partie numérique de la petite enquête sur la modélisation, nous allons plutôt nous centrer sur ce qu’il est souhaitable et possible de faire dans nos classes.
La question de fond est certainement celle du désir épistémologique (praxéologique dirait Yves Chevallard) des élèves, désir couplé à la quête du sens, deux moteurs solidaires un peu en panne dans nos classes de mathématiques, et ce, malgré la multitude d’initiatives dont la communauté fait montre. La pandémie actuelle a sans aucun doute accentué l’inappétence pour l’étude, flagrante aujourd’hui semble-t-il dans nos classes de Seconde. Le problème épistémologique vient de loin, probablement du moment où les mathématiques dites pures ont chassé des curricula de tous les niveaux les mathématiques dites appliquées, l’exposé des synthèses – plus facile à construire – consumant alors tout le temps disponible. Souvenons-nous de nos études universitaires : un flot de réponses sans question ; des applications à l’importance proclamée le premier quart d’heure et arrivant rarement ou de façon anecdotique. Ainsi dans tel certificat de probabilités, on étudiera la loi faible des grands nombres, puis la forte, puis le TCL, puis en travaux dirigés un raffinement d’hypothèses ou d’inégalités, mais sans jamais de réponse sérieuse à la question de l’utilité. Au point que le mot « appliquées » en a perdu son sens ancien. La modélisation nous est présentée comme une possibilité de recréer du désir d’étude et du sens. Acceptons le terme malgré sa prétention.
Le lecteur intéressé par les origines du courant modélisation dans la pensée scientifique, qui démarre franchement au début du XXe siècle avec Alfred James Lotka, pourra consulter l’ouvrage de Giorgio Israel : La mathématisation du réel.
Concernant le monde de l’éducation, le mouvement vient des États-Unis : en 1980, la Mathematical Association of America publiait les quatre volumes de Modules in applied mathematics, fruit du travail d’une soixantaine de scientifiques polyvalents comme ils le sont plus facilement outre-atlantique. Les titres des volumes en disent amplement sur leur contenu qui ne se réduit pas à de simples exercices d’application des mathématiques : differential equations models, political and related models, discrete and system models, life science models.
En France, l’idée de son introduction dans la classe de mathématiques se situe dans les années quatre-vingt dix, après le constat de la non-viabilité du retour aux problèmes concrets amorcé en 1981. L’idée devient réalité avec l’introduction des TPE et de l’épreuve de modélisation à l’agrégation externe de mathématiques en 1999. Sa viabilité dans la classe s’est avérée fort problématique, peu compatible avec un enseignement « traditionnel » (sans intention péjorative dans ce qualificatif).
On notera que les programmes n’emploient que le verbe « modéliser » dans la liste des compétences, qui peut suggérer – avec pertinence ou réalisme – une prise en compte dans des projets d’ambition modeste, voire de simples exercices et de saisir les occasions sans bouleverser ses pratiques. En réalité, les modèles sont déjà là, partout dans les mathématiques.
Au sens premier, on trouve les maquettes :
| En 1978 était publiée par les défuntes éditions CEDIC, la traduction française de l’ouvrage de Cundy et Rollett : mathematical models dont la première édition remonte à 1951. La table des matières en signifie bien le contenu, s’adressant à des élèves de 16-17 ans : Modèles en géométrie plane — Polyèdres — Modèles en géométrie dans l’espace — Modèles mécaniques — Modèles pour la logique et le calcul. Il est fort amusant de faire la comparaison avec le contenu d’un manuel de Première A-B-C ou D de 1978. À la même époque, le regretté Charles Pérol, grand militant avant l’heure de l’expérimentation en mathématiques, imaginait le filicoupeur comme outil pour l’étude des polyèdres. Voir https://publimath.univ-irem.fr/biblio/AAP78020.htm Dans cette acception, l’abstrait est du côté de l’objet : un polyèdre est un objet bien difficile à définir ; les modèles en papier ou en polystyrène en sont une version concrète bien utile si, par exemple, on cherche les géodésiques (plus courts chemins) du cube. |
Acceptons d’appeler « modèle » toute construction manuelle ou intellectuelle ou logicielle qui apporte une aide à la compréhension d’une notion, d’un concept, ou à la résolution d’un problème. Mais ne quittons pas les mathématiques.
| D’une certaine façon, le traditionnel dessin représentant un problème de géométrie mérite déjà l’appellation de modèle : il s’agit bien d’une mise en symboles (graphiques) que la pensée peut utiliser ; construit avec des instruments, il est souvent plus efficace et réalisé avec un logiciel, il devient dynamique et, par là même, modèle d’un objet plus abstrait : la figure. Une carte topographique au (1/15000) est bien le modèle d’un lieu, permettant de participer à une course d’orientation s’y déroulant. |
Mais en un sens plus abstrait :
| Les égalités \(2 \times 3 = 6\), \(3=\dfrac{6}{2}\), \(2=\dfrac{6}{3}\) forment un modèle des transformations valides de \(a\times b = c\), utile même en seconde. Les représentations graphiques des fonctions en sont des modèles remarquablement efficaces et pas seulement dans le cas d’une variable. Si \(h=f(x,\,y)\) est une certaine fonction (sympathique) de deux variables dont on recherche bosses, creux et cols dans un pavé \([a\,;\,b]\times [c\,;\,d]\), une représentation graphique par courbes de niveaux est un modèle performant pour répondre à cette question, modèle accessible à des élèves de Quatrième1. Les formules ne sont pas en reste : \(y=a\,x+b\) est un modèle des droites, \(x=v\,t\) est un modèle du mouvement uniforme, \(\vec{f}=m\,\vec{\gamma}\) un modèle de la dynamique du point matériel, \(h=h_0\,\cos(\kappa\,(x+v\,t)+\Phi)\) est un modèle pour une onde progressive. L’implication logique est présentée (par les logiciens) comme modèle du « si …, alors » … de nos cours. |
Loin des grandes constructions didactiques, admettons comme principe pédagogique d’action que ce qui devrait être premier dans les apprentissages, c’est, appuyé sur une envie de savoir suffisante, ce que les élèves font effectivement par elles-mêmes, la parole professorale, utile certes, s’avérant inopérante per se. En allant un peu plus (trop ?) loin, on peut pousser le bouchon jusqu’à vouloir faire en sorte que, au moins en certaines circonstances, chacune puisse rendre accessible à elle-même les outils mathématiques utiles au but poursuivi. Et ce « faire » est souvent plus efficace dans l’interaction qu’isolée, cette maxime valant aussi côté professeure.
Pour cela, il convient de partir de problèmes faisant sens pour le public concerné, problèmes intra ou extra-mathématiques. Si le problème est en prise sur les centres d’intérêt de l’instant, c’est mieux ; pour l’enseignant, cela s’appelle l’agilité, compte Instagram impératif pour sûr.
On parle ici de problème non trivial pour lequel un algorithme de résolution n’est pas nécessairement disponible pour celui qui cherche, un problème qui n’est pas un réinvestissement plus ou moins immédiat de connaissances acquises par ailleurs (ce qui pourrait déjà procurer une première satisfaction). Ce qui compte, c’est que l’étude du problème suscite le besoin d’une connaissance nouvelle, possiblement modeste mais signifiante ; c’était l’intention de la vieille idée de situation-problème. Et si le travail réalisé contribue à justifier l’utilité sociale de la discipline, c’est un peu le jackpot. Pour cela, il n’est nul besoin de plonger dans la complexité réelle du réel pour faire faire un travail de modélisation à une élève, un petit groupe d’élèves ou toute une classe.
Dans [1] , Michel Soufflet (bien connu des membres de l’APMEP) donne l’exemple suivant d’une occasion saisie promptement2 :
| Un élève de Première S lui demande comment calculer l’angle entre l’atome de carbone et deux des atomes d’hydrogène dans une molécule de méthane (que le professeur de physique a déclaré égal à 109 degré). Voilà un problème qui peut initier une (modeste) recherche pour un élève ou un groupe d’élèves intéressés par la question et la question s’avère riche. La mathématisation est simplement le tétraèdre régulier et son centre (validée par le physicien ou alors c’est une autre enquête) mais justement, c’est quoi le centre d’un tétraèdre ? Un isobarycentre ? Ou peut-être y a-t-il un rapport avec le centre d’une sphère et que sont ces droites joignant les sommets au centre ? Le laboratoire de chimie possède peut-être des éléments de construction de molécule pour faire un … modèle. La mathématisation peut aussi relever de la géométrie 3D repérée, la difficulté résidant dans le choix du repère qui peut être pertinent ou pas du tout ; mais les fausses pistes font partie du travail de recherche. De diverses façons, dont la plus élémentaire relève du simple rapport : côté adjacent sur hypoténuse, on peut aboutir à \(\cos(\theta)=-\dfrac{1}{3}\cdotp\) Le calcul de \(\theta\) peut alors se faire en dégainant une calculatrice ou éventuellement rebondir sur une nouvelle enquête. La connaissance nouvelle concerne la géométrie du tétraèdre régulier, généralisant celle du triangle équilatéral ; et, possiblement, une nouveauté : un tétraèdre régulier est inscriptible dans un cube. |
Chevallard, dans un certain nombre d’écrits [2] , a insisté sur les vertus de la calculatrice, « ce bon objet » et sur un certain nombre de « croyances » durablement installées dans la profession qu’un peu de mathématisation algébrique permet de corriger.
| Empruntons lui le signe \(=_{\textrm{calc}}\) pour désigner l’identité d’affichage sur une calculatrice de deux calculs. Alors on peut correctement asserter : \(\dfrac{209}{347}=_{\textrm{calc}}\dfrac{1\;463}{2\;429}\), donc \(\dfrac{209}{347} = \dfrac{1\;463}{2\;429}\) ; mais on ne peut pas faire la même déduction à partir de \(\dfrac{1\;607\;521}{1\;136\;689} =_{\textrm{calc}} \dfrac{3\;880\;899}{2\;744\;210}\). Dans le premier cas, si les deux quotients étaient différents, la différence se verrait à partir de la sixième décimale. Par contre, dans le second cas, ce serait seulement à partir de la douzième et là, avec une calculatrice standard, il y a doute. |
La réalité de la gestion des classes nous pousse vers ce qu’Alain Bouvier appelait la pédagogie des petites marches : une notion à la fois, bien assimilée avant d’aborder la suivante, avec des exercices progressifs, d’autant plus nombreux que la notion est jugée importante. Description caricaturale mais pertinente : cette façon de faire, qui a bien les vertus d’une certaine économie, d’une optimisation du temps (les manuels sont ainsi faits), d’une ré-exploitation facilitée des cours, mais a l’inconvénient de générer plutôt la passivité et donc l’ennui. Il faut peut-être accepter, qu’occasionnellement, la classe puisse être plongée dans une situation plus stimulante, voire compliquée, dont le contenu mathématique peut dépasser les connaissances du public concerné mais en suscitant le désir de savoir. Le déclencheur peut-être un fait d’actualité, un article dans une revue scientifique (il n’en manque pas), ou un des nombreux évènements initiés par la noosphère : une conférence (ou une visio-conférence), une participation à un des divers rallyes organisés dans les établissements, voire un escape game. Cela peut conduire à quelques affiches, à un sujet d’étude (sous forme de devoir libre en tout petit groupe à questions plus ouvertes que dans un devoir traditionnel), ou encore à un même exposé réalisé par deux groupes de deux ou trois volontaires avec des contraintes d’exposition stricte (durée, nombre de diapos, partage de la parole, …). Les IDD puis les TPE apportaient une réponse et un cadre institutionnel à cette problématique ; il est probable que le développement de la Toile a plutôt favorisé la recherche de réponses clés en main. C’est évidemment aujourd’hui une règle du jeu à laquelle il n’est plus possible d’échapper.
Dans le propos ci-dessus, le occasionnellement n’est pas qu’une précaution de langage posée là pour ne pas effrayer le lecteur. Changer le contrat n’est pas simple et loin d’être sans risque ; et l’évaluation doit être négociée auparavant ; la recherche demande plus d’effort et de persévérance.
Il y a déjà fort longtemps – à une époque où le WWW naissait dans l’esprit de Tim Berners-Lee, et dans le cadre d’une pratique occasionnelle de problèmes ouverts3, la question suivante fut proposée à une classe de seconde :
| Peut-on voir l’île Maurice depuis l’île de la Réunion ? Un élève d’origine mauricienne ramena de chez lui la formule suivante, surprenante par sa simplicité : \(d=\sqrt{h}\) dans laquelle \(d \) est la distance à laquelle peuvent voir des yeux situés à la hauteur \(h\). Surprise et recherche (laborieuse) pour l’enseignant : comprendre que \(h \) est exprimé en pied et \(d\) en mille nautique, ce que l’élève concerné n’avait pas saisi. |
À la même époque, Marc Legrand [3] proposait de construire le « sens profond » de l’intégration à partir de quelques problèmes conçus pour faire émerger les propriétés caractéristiques de l’intégration. Par exemple :
\(\bullet\) Calculer la force d’attraction qu’exerce une barre homogène fine de 18 kilogrammes et de 6 mètres de long sur une masse ponctuelle de 2 kilogrammes dans les deux situations suivantes :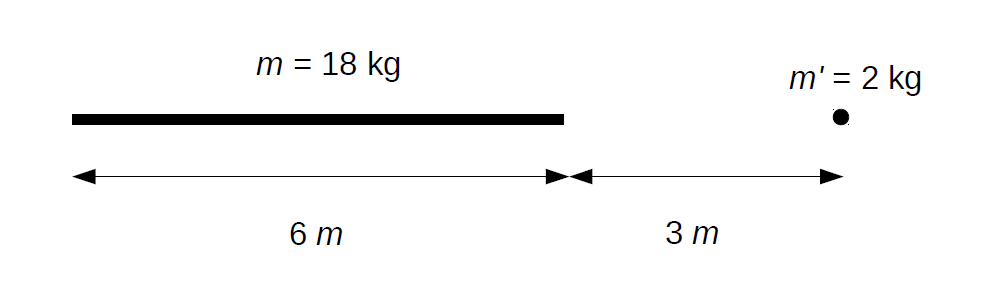 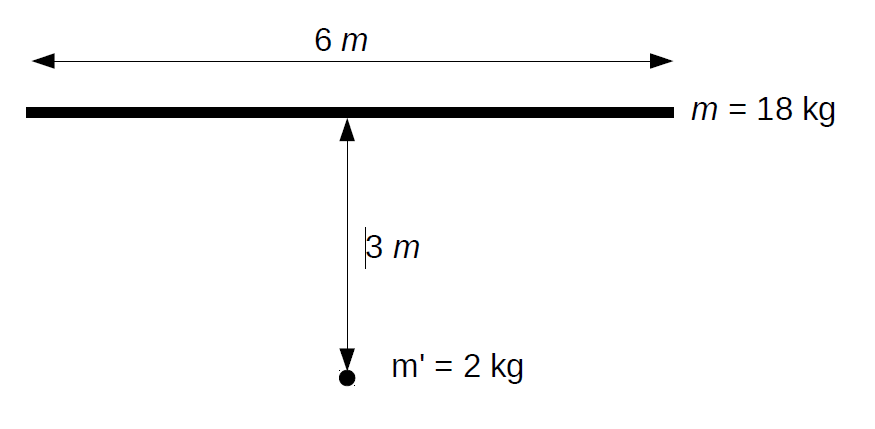 La loi de gravitation universelle est rappelée : \(f=G \dfrac{m_1 \,m_2}{r^2}\cdotp\) \(\bullet\) Calculer le volume d’un étang pour lequel on fournit une carte à l’échelle 1/5 000 et des courbes isobathes (courbes d’égale profondeur). |
L’introduction d’une dose non cosmétique de statistiques au lycée a offert aux enseignants de remarquables possibilités de s’intéresser à des problèmes ancrés dans des préoccupations possiblement porteuses d’envie et de sens.
| L’affaires Woburn est un exemple de la vraie vie où la justice a usé de la statistique pour se prononcer. Le problème a pu être posé ainsi [4] : Une petite ville des États-Unis a connu 9 cas de leucémies chez de jeunes garçons en l’espace de 10 années. Doit-on en « accuser le hasard » ? |
Joli paradigme d’invitation à l’enquête. L’institution a juste oublié que, sorti du calcul de moyennes, de médianes et autres boîtes à moustaches – horizon statistique en Seconde avant l’épisode fluctuation-confiance, la statistique inférentielle était absente de la formation de 95% des enseignants (y compris du supérieur) et que la matière, appliquée par nature, n’est pas si aisément accessible comme en témoigne magistralement les polémiques entre « experts » qui n’ont pas manqué de survenir, comme toujours lorsqu’on aborde des questions socialement vives [5].
L’introduction consistante de probabilités dans les programmes a fourni aussi de nombreuses occasions de questionnements ainsi qu’en atteste l’énorme quantité de publications sur le sujet depuis une vingtaine d’années ; le couple (probabilités, modélisations) se fait alors très remarquer ; par exemple disponible [6] sur Publimath.
D’autres difficultés se présentent lorsque le problème sort franchement du champ mathématique. On pense bien sûr à la physique, matière certainement la plus proche de la nôtre, mais aucune discipline n’est exclue. Dans l’ordre ordinaire de la division du travail – « chacun chez soi et les moutons seront bien gardés » – et dans un monde parfait, l’élève étudie en mathématiques une certaine technique (par exemple au collège, l’écriture sous forme scientifique du résultat d’un calcul numérique avec un embryon de réflexion sur les décimales significatives et sur la vraisemblance du résultat par estimation de l’ordre de grandeur) et le physicien de seconde peut utiliser un savoir-faire dûment acquis dans ses applications numériques en ajoutant une connaissance nouvelle sur le caractère significatif des décimales et la vraisemblance en physique. Bien sûr, les choses se passent rarement ainsi et le physicien est bien obligé de mettre les mains dans le cambouis du calcul numérique, avec guère plus de succès, ce qui repousse le problème au cursus suivant qui lui, n’a plus le temps.
La modélisation invite les enseignants à la co-disciplinarité, un concept apparu en même temps que celui de démarche d’investigation, moins ambitieux que celui d’interdisciplinarité, ce dernier n’ayant pas vraiment engendré d’enthousiasme dans les décennies précédentes. Il s’agit nullement de traiter des questions de physique dans le cours de mathématiques (mais d’ailleurs pourquoi pas ?), mais d’utiliser un problème s’originant dans le réel physique et d’imaginer un travail en commun de deux disciplines, chacune poursuivant des objectifs particuliers, avec l’idée qu’il peut y avoir plusieurs niveaux d’approfondissement dans un tel problème. Le lecteur qui a du temps pourra se plonger dans les 1697 pages des Actes du Colloque EMF 2018, Mathématiques en scène, des ponts entre les disciplines disponible sur Publimath.
| L’exploit du saut en parachute en 2012 de Felix Baumgartner franchissant le mur du son peut inciter à enquêter sur la relation entre vitesse atteinte et hauteur du saut et, possiblement, à élaborer des modèles à base d’équation différentielle \((\ddot{x}=-g)\) et au physicien d’inciter à enquêter sur la physique fort riche de ce phénomène. |
Cette co-construction peut tout à fait nécessiter l’appel à des notions ou des techniques hors-programmes ; ceci ne doit pas constituer un obstacle ou un repoussoir a priori : c’est un fait banal que, dans les études scientifiques, on utilise en aveugle, logiciels aidant, des techniques dont on ne maîtrise pas nécessairement la théorie, ni même la pratique manuelle d’ailleurs ; l’important est de pouvoir interpréter correctement les résultats obtenus ce qui est une autre compétence.
Quelques observations sur les modèles
Entendons la modélisation (mathématique) dans la classe comme la totalité d’un processus au service de la résolution d’un problème, de la construction d’une réponse, éventuellement partielle voire erronée, à une question. C’est dire que la modélisation est entendue comme synonyme de résolution de problème, mais en laissant à la charge de l’élève (des élèves) une part significative du travail de la mise en mathématiques. Redisons que le problème peut être d’origine mathématique. Le modèle proprement dit est une étape de ce processus.
Le dans la classe est important ; toute action entreprise dans la classe doit s’insérer dans une organisation en place, faite d’un réseau de contraintes rigidifiantes, au premier rang desquelles l’emploi du temps. Les marges de manœuvre de l’enseignant sont étroites.
Les mathématiques offrent à l’apprenti modélisateur une panoplie d’objets : un simple nombre, une grandeur, un vecteur, une matrice, un graphe, un arbre, un ensemble, une droite, un plan, un dessin en perspective cavalière, une courbe, un polynôme, un diagramme, une suite, une fonction, un algorithme … Ces objets permettent de coder de l’information, en apportant avec eux une combinatoire – typiquement un calcul – porteuse de significations relativement à cette information. C’est la fonction de représentation des objets mathématiques.
Le travail de modélisation, après le choix d’un objet pertinent, peut imposer des propriétés à cet objet, de façons diverses ; les divers secteurs des mathématiques : algèbre, analyse, géométrie, probabilités, peuvent être sollicités. Une petite promenade s’impose.
| On trouvera le compte-rendu du traitement d’une situation concrète d’optimisation, fort classique, mais instructive dans la manière de la mener, ici. |
La dynamique des populations est sans doute un domaine privilégié pour susciter de petites enquêtes car elle autorise des modélisations (mathématiques) d’une grande diversité et d’un large éventail de complexité, mais la collaboration d’un « expert » semble de rigueur ; la Toile n’est pas une ressource magique.
| Comment estime-t-on une population donnée (et son évolution) à partir des comptages ou des prises de pêche ? Comment ces comptages permettent-ils de mettre en évidence l’influence du changement climatique sur les espèces migratoires. Les mathématiques utiles sont élémentaires : boîtes à moustaches, diagrammes divers, un peu d’ajustement. Malheureusement la documentation n’est pas si simple à rassembler et rarement dans la langue de Molière. |
La géométrie, une vieille dame mais qui accompagne toujours de nombreux corps de métier peut être sollicitée ; ainsi le problème des raccordements progressifs joliment décrit par Frédéric Vivien dans la publication de l’IREM de Rouen Géométrie et raccordements de routes en Haute-Normandie disponible sur Publimath.
| Si on veut raccorder deux sections de route rectilignes (dans le même plan pour commencer !) faisant un certain angle, éventuellement très aigu, il convient de puiser dans le réservoir des courbes disponibles : cercle, parabole et autre représentation graphique. On sera amené à questionner le caractère suffisant d’un raccord lisse (tangent) et tutoyer le concept de courbure lié à la rotation du volant, déjà pour un cercle, puis pour une parabole ; la possibilité de n’utiliser que des arcs de cercles suivant le positionnement relatif des sections peut être envisagée. Utiles aussi les techniques utilisées par les géomètres pour figurer le tracé au sol : le piquetage. Il existe tout un savoir-faire géométrique, qui tend peut-être à se perdre, logiciels et GPS aidant. |
Parfois, il est possible de s’appuyer sur des particularités locales :
| Avant les constellations de satellites et le GPS, existait le système de navigation OMEGA, reposant sur les émissions de huit antennes de plus de 400 mètres de haut réparties sur tout le globe. Les signaux de trois antennes étaient nécessaires pour obtenir une géolocalisation de l’ordre du mille nautique. L’objet mathématique de base est l’hyperboloïde à deux nappes – surface isophase des signaux émis par deux antennes, mais dans le plan horizontal local, c’est l’hyperbole, via sa définition bifocale (et peu importe qu’elle soit ou non au programme). L’antenne installée à Saint-Paul (Réunion), aujourd’hui détruite, a suscité bien des visites, des enquêtes conjointes avec le collègue de physique, des exposés, des petits sujets d’étude, ne serait-ce que la mesure de sa hauteur (l’accès au site étant interdit donc le pied de l’antenne a priori inaccessible) à l’aide de deux mesures angulaires et d’un dessin à une échelle ad hoc. Rien d’extraordinaire (et beaucoup de travail), juste un rapport au savoir différent. Le système GPS n’est pas fondamentalement différent mais contient bien plus et de physique et de mathématiques (géodésie, ondes électromagnétiques, relativité restreinte, mesure du temps, algèbre linéaire, moindres carrés) ce qui permet de gagner un facteur \(10^5\) dans la précision. |
L’astronomie de position est un autre remarquable réservoir de problèmes ne nécessitant pas de mathématiques intersidérales. Le couple mathématiques-astronomie est multi-millénaire et, dans l’enseignement, les mathématiques ont toujours eu pour l’astronomie les yeux de Chimène. Depuis 1978, paraissent les Cahiers Clairaut4, bulletin de liaison Enseignants et Astronomes ; les IREM et le bulletin vert ont largement enrichi la documentation.
L’astrolabe et les cadrans solaires sont des instruments fascinants pour un amateur de mathématiques ; on pourra consulter, outre les cahiers Clairaut, la publication de l’IREM de Paris-Nord L’astrolabe au carrefour des savoirs (disponible sur Publimath) réalisée pour le thème TPE : » Mesure du temps ou la véritable encyclopédie » de Raymond d’Hollander L’astrolabe : histoire, théorie et pratique.
Les passages de Vénus (devant le soleil) constituent des évènements exceptionnels pour l’astronomie fondamentale (mesure des distances dans le système solaire) et pour les hommes (2004, 2012, puis 2117 … ). Ceux de Mercure sont plus fréquents.
| Un très joli TP abordable au lycée est la construction sur papier (format A3, voire A2) de l’orbite héliocentrique de la terre et de Mars par la méthode de Kepler : à partir des seules longitudes géocentriques écliptiques du soleil et de Mars mesurées à des dates bien choisies qui demandent soit plusieurs années de mesure ( !), soit de consulter des éphémérides, on construit (avec un peu de géométrie angulaire) une dizaine de positions, puis on trace une ellipse optimale (visuellement) par la méthode du jardinier. Pour ne pas être trop has been, on peut remplacer le papier-crayon par Geogebra. La loi des aires de Kepler est alors à portée de main. |
On perçoit bien la dialectique qui pourrait s’opérer entre connaissance de l’objet et utilisation de l’objet alors que nous avons, par formation, tendance à penser que les applications ne peuvent arriver qu’après une solide étude des objets, comme illustration du déjà compris.
Il ne semble pas possible de donner une description raisonnable d’un processus de modélisation qui soit utile aux niveaux considérés ; la didactique s’y essaye, des spécialistes de théorie des systèmes aussi [7] mais il y a autant de modélisations que de modélisateurs et même, que de problèmes à résoudre (on parle de problème nouveau). La définition d’un modèle comme représentation d’un système réel est déjà problématique en renvoyant à la notion de système et à celle de représentation. Mais on peut s’en satisfaire.
Du point de vue épistémologique, Israel [8] isole deux caractéristiques de la modélisation à l’œuvre aujourd’hui :
- Le renoncement au rêve scientiste du XIX siècle d’une vision unifiée et mécaniste de la nature écrite en langage mathématique. Il n’y a pas un seul modèle possible pour décrire un morceau de réalité et chaque modèle mathématique peut représenter des morceaux de réalité a priori sans rapport. Ce qui peut questionner sur le caractère explicatif des modèles.
- La méthode fondamentale d’élaboration d’un modèle est l’analogie mathématique se substituant à l’analogie mécaniste dont le paradigme est le modèle de Van der Pol et Van der Mark (1920) des battements cardiaques ; un même modèle peut, par analogie interne aux mathématiques (oscillations auto-entretenues avec relaxation) s’appliquer à différents morceaux de réalité.
Cette deuxième caractéristique vaut particulièrement pour les sciences du vivant, vivant biologique ou social, et moins pour les sciences physico-chimiques reposant sur des lois bien établies fournissant des modèles clés en main.
Quelques invariants dans le processus de modélisation peuvent être isolés, plus ou moins pertinents, utiles à l’intelligence de la modélisation, compréhensibles par un lycéen et condensées dans les quatre critères suivants :
minimalité, vraisemblance scientifique, cohérence, validation
- Le critère de minimalité incite à ne mettre pas plus de mathématiques dans un modèle qu’il n’est utile pour obtenir un peu de pouvoir explicatif. Autrement dit, le mot d’ordre est : « pour commencer, faire simple ! » . Et la simplicité en mathématiques est souvent synonyme de linéarité.
Bien sûr, ce critère entre en conflit avec la prise en compte de la complication du système étudié. C’est une évidence : l’approximation, voire l’inexactitude est inhérente au processus de modélisation.
| Si on veut étudier la chute libre d’un parachutiste, on commencera par négliger la résistance de l’air. Pour l’étude de la propagation d’un virus, on supposera que chaque personne contaminée en contamine à son tour un certain nombre \(R\) (sans se poser la question du caractère entier ou non entier de \(R\)). |
- Le critère de vraisemblance scientifique demande qu’un modèle ne se contente pas de bien « matcher » les données expérimentales, mais aussi, qu’on puisse en fournir une explication raisonnée a priori fondée sur les acquis scientifiques de la discipline considérée. L’analogie mathématique doit pouvoir être justifiée, éventuellement a posteriori. Ce point est d’actualité : un modèle mathématique ne saurait être performatif et se substituer à la poursuite de la connaissance scientifique : le modèle n’est pas la réalité.
| Dans le problème du parachutiste, l’introduction d’une force de freinage proportionnelle au carré de la vitesse fournit un modèle qui « colle » mieux aux données réelles qu’une force de freinage proportionnelle à la vitesse (modèle linéaire). La dynamique des fluides valide a priori cette hypothèse. |
- Le critère de cohérence : le modèle ne doit pas introduire de contradiction ou conduire à des grandeurs prenant des valeurs incompatibles avec leur signification physique : masse ou population négatives, température non bornée,… Ce critère peut amener à imposer certaines contraintes aux variables introduites, par exemple limiter l’intervalle de la variable temporelle dans un modèle d’évolution.
| Si un premier modèle de chute libre conduit à une vitesse de 720 km/h pour une chute libre de 2 000 m, il doit être rejeté (ou modifié), cette vitesse n’ayant jamais été observée. |
- Le critère de validation demande de préciser les clauses permettant de valider le modèle par l’observation, l’expérimentation ou la simulation, avec bien sûr un peu de statistiques à la clé. Tout ce qu’un modèle est en mesure de calculer n’est pas nécessairement observable. Ce critère est capital car il doit permettre de juger de l’adéquation du modèle à la réalité qu’il prétend décrire 5.
| Dans le problème du parachutiste, le modèle avec force de freinage proportionnelle au carré de la vitesse et en deux parties : chute libre puis chute avec parachute, conduit à un jerk6 de plusieurs dizaines de \(g\) incompatible avec la survie du parachutiste. Il convient alors d’introduire une troisième partie : l’ouverture du parachute… |
Il faut être conscient que, si un modèle est censé posséder certaines propriétés de ce qu’il modélise, aucun modèle ne peut être parfait, c’est-à-dire tel que toute propriété du modèle soit une propriété du système réel modélisé, et non plus complet, c’est-à-dire tel que toute propriété du système soit aussi une propriété du modèle.
Une fois le modèle élaboré et adimensionné, commence alors le traitement mathématique du modèle lequel éventuellement par voie logicielle ; les questions posées peuvent être diverses et font sens pour des équations différentielles, des récurrences, des équations ou des systèmes d’équations, des intégrales, une loi de probabilité, etc. Isolons quelques questions transversales :
- Le problème a-t-il (au moins) une solution ? Ici la réponse « oui, puisque le système physique existe et évolue » est un contre-sens. Si oui, en a-t-il une seule ?
- Pour avoir l’unicité dans un modèle, on a en général besoin de condition(s) supplémentaire(s) ; par exemple dans un problème d’évolution, de(s) condition(s) initiale(s).
- Un modèle comporte presque toujours des paramètres ; peut-on les identifier avec les données disponibles ? Comment la solution dépend-elle de ses paramètres ?
- Cette solution est-elle calculable (en un sens qui aura bien besoin d’être précisé) ?
- Peut-on définir et calculer une forme approximative de cette solution ? Et peut-on mesurer la qualité de cette approximation ? En particulier l’équation est-elle stable numériquement ?
- Que se passe-t-il si on fait des approximations sur l’équation elle-même ? Les solutions exactes de l’équation approchée ont-elles quelque chose à voir avec les solutions exactes de l’équation exacte ?
- Les calculs précédents apportent-ils des réponses aux questions à l’origine du modèle ? Les calculs sont-ils en accord avec les résultats expérimentaux ? Le modèle est-il aussi validé par sa capacité prédictive ?
- Si le calcul ou la simulation conduise à des résultats incompatibles avec les données, peut-on analyser l’origine de ces divergences et modifier le modèle ?
Discret versus continu
Examinons le passage discret-continu dans les modèles de population passage conceptuellement délicat en suivant [9].
On cherche à modéliser l’évolution de la population humaine mondiale \(N=N(t)\) comme fonction du temps. On dispose de données assez fiables depuis, disons 1800 jusqu’à nos jours. On souhaite faire des projections pour les décennies à venir.
À l’instant initial \(t_0\), on a \(N(t_0)=N_0\) ; considérons un intervalle de temps \(\Delta \,t\) qui sera précisé ultérieurement et qui pour l’instant nous sert d’unité de temps, et posons \(N_n=N(t_0+n\,\Delta\,t)\). Le taux de variation de cette population entre les instants \(t\) et \(t+\Delta \,t\) est par définition le quotient \[\dfrac{\Delta\, N}{\Delta\,t}=\dfrac{N(t+\Delta)-N(t)}{\Delta\,t}\cdotp\] Les démographes préfèrent considérer le taux de croissance à l’instant \(t\) per capita : \(\displaystyle R(t,\,\Delta\,t)=\dfrac{N(t+\Delta\,t)-N(t)}{N(t)\,\Delta\,t}\cdotp\)
Si \(b\) est le taux de natalité \(\left(b=\dfrac{\# \textrm{ naissances}}{N(t)\,\Delta\,t}\right)\), \(d\) le taux de mortalité \(\left(d=\dfrac{\# \textrm{ décès}}{N(t)\,\Delta\,t}\right)\), on a alors7 : \(R=b-d\).
Dans le modèle le plus simple (Malthus), on prend \(R(t,\Delta\,t)\) constant, égal à \(R_0(\Delta\,t)\) qu’on notera simplement \(R_0\) dans la suite mais il dépend bien de \(\Delta\,t\).
Le modèle discret est alors le modèle géométrique : \(N_{n+1}=(1+R_0\,\Delta \,t)\,N_n\) qui se résout en : \[N_n=(1+R_0\,\Delta\,t)^nN_0\] qu’on peut réécrire, en posant \(t=t_0+n\,\Delta t\) :
\(N(t)=\big(1+R_0\,\Delta\,t\big)^{\textstyle\frac{t-t_0}{\Delta\,t}}\,N_0= N_0\, \text{e}^{(t-t_0)\,\textstyle\frac{\ln(1+R_0\,\Delta\,t)}{\Delta\,t}}\).
Il faudrait bien sûr préciser le champ de validité a priori du modèle, c’est-à-dire l’intervalle de variation pour l’entier \(n\).
A priori, on peut choisir \(\Delta\,t\) arbitrairement. Mais pour rendre plausible l’hypothèse sur \(R(t,\,\Delta t)\) il faut prendre \(\Delta \,t\) assez grand pour que, par effet de moyenne, les fluctuations à petite échelle temporelle soient gommées. Le lecteur trouvera tout seul d’innombrables raisons pour expliquer qu’un \(\Delta\,t\) de l’ordre de l’année est bien adapté à la population humaine (mais pas à celle des neutrons dans une pile à combustible).
Parlons maintenant données : a priori, \(N(t)\) est, quelque soit \(t\), un entier. L’ordre de grandeur de \(N\) est \(6 \cdot 10^9\) ; celui du \(\Delta\,N\) annuel est \(10^8\) ; sachant qu’il y a en gros \(3\cdot 10^7\) secondes dans une année, la population augmente en moyenne de \(3\) à \(4\) individus chaque seconde. À l’échelle d’une année, il est donc raisonnable de considérer \(N\) comme une fonction continue du temps \(t\) à valeurs dans \(\mathbb{R}^+\). Cela devient très raisonnable si on prend comme unité de dénombrement \(10^5\) individus.
Ce pas essentiel franchi, il n’est pas plus coûteux de supposer que \(N\) est une fonction dérivable du temps, ce qui permet d’introduire la taux de croissance instantané à l’instant \(t\) : \[R(t)=\lim_{\Delta\,t \to 0}\dfrac{N(t+\Delta\,t)-N(t)}{N(t)\,\Delta\,t}=\dfrac{1}{N(t)}\dfrac{\text{d}N(t)}{\text{d}t}\]
En supposant à nouveau \(R\) constant, le modèle de croissance de la population devient alors : \(\dfrac{N(t)}{\text{d}t}=R_0\,N(t)\) qui pour la condition initiale \(N(t_0)=N_0\) se résout en : \(N(t)=N_0\,\text{e}^{R_0(t-t_0)}\) avec un intervalle de variation pour \(t\) à préciser, soit a priori à partir de l’hypothèse \(R\) constant, soit a posteriori par confrontation à l’expérience.
On se doit de comparer les deux modèles ; un \(DL_2(0)\) de \(\ln(1+x)\) fournit : \(\dfrac{\ln(1+R_0\,\Delta\,t)}{\Delta\,t}=R_0-\dfrac{\Delta\,t}{2}R_0^2+o(R_0^2\,\Delta\,t)\)
On notera que \(R_0\,\Delta\,t\) est sans dimension. Les deux modèles fournissent des résultats similaires, pour des \(t\) de l’ordre de l’unité de temps, si \(R_0\,\Delta\,t \ll 1\). Pour \(\Delta\,t=\)1 an, on a \(R_0 \approx 0,02\). Une expérience numérique est facile.
Il est aussi intéressant d’étudier l’évolution de la population des divers pays (par exemple la France) en tenant compte du solde migratoire sur des périodes courtes (10 ans) et de comparer cette évolution avec celle fournie par le modèle local tangent au modèle malthusien. Les données sont abondantes.
L’exemple précédent montre que l’on peut passer sous certaines conditions d’une équation aux différences à une équation différentielle par passage à la limite sur la variation de la variable indépendante. L’équation différentielle apparaît alors comme une approximation pour modéliser un phénomène dans lequel la population est a priori discrète, mais :
- les changements y sont permanents ;
- ils concernent une population assez large et des événements assez nombreux en moyenne ;
- l’échelle de temps sur laquelle ces moyennes sont examinées est grande devant celle des événements particuliers.
C’est exactement l’hypothèse mésoscopique (existence d’un niveau intermédiaire entre le microscopique et le macrocospique qui permet d’introduire la « particule fluide » sur laquelle les raisonnements différentiels sont possibles) de la mécanique des fluides.
D’autre part, on sait qu’à l’inverse, la méthode d’Euler permet d’associer à une équation différentielle une suite récurrente, la théorie précisant sous quelles conditions l’association est valide, c’est-à-dire fournit des informations correctes.
Mais il existe d’autres méthodes d’associer un modèle discret à un modèle continu. L’une consiste à associer (avec une audace toute infinitésimale) aux dérivées des fonctions ce qu’on appelle les dérivées discrètes des suites :
\(f'(t)=\dfrac{f(t+\text{d}t)-f(t)}{\text{d}t}\ \leftrightarrow \ \Delta u_n=\dfrac{u_{n+1}-u_n}{1}\)
\(f »(t)= \dfrac{f(t+\text{d}t)-2\,f(t)+f(t-\text{d}t)}{\text{d}t^2}\ \leftrightarrow \ \Delta^2_{-1} u_n=\dfrac{u_{n+1}-2\,u_{n}+u_{n-1}}{1^2}\)
Il faut comprendre le \(1\) au dénominateur de \(\dfrac{u_{n+1}-u_n}{1}\) comme une unité de la grandeur \(t\), le \(n\) de \(u_n\) comptant le nombre d’unités de temps depuis l’instant initial, ce qui permet d’assurer la cohérence dimensionnelle ; ainsi si \(\tau\) est un temps caractéristique choisi pour le phénomène évolutif étudié, alors il faut comprendre \(u_n\) comme \(f(t_0+n\,\tau)\) et \(\dfrac{u_{n+1}-u_n}{1}\) comme \(\dfrac{f(t_0+(n+1)\,\tau)-f(t_0+n\,\tau)}{\tau}\). On voit qu’il vaut mieux avoir adimensionné le problème avant de le discrétiser.
Ainsi à l’équation différentielle \(y’ ;=a\,y+b\) sera associée la récurrence \(u_{n+1}-u_n=a\,u_n+b\) soit \(u_{n+1}=(1+a)\,u_n+b\).
Ce procédé est très séduisant parce que, d’une part, la justification scientifique du modèle discret est la copie (prudente) de celle du modèle continu, et d’autre part les dérivées discrètes possèdent des propriétés formelles tout-à-fait similaire à celles des dérivées des fonctions. On peut espérer une « convergence » des dynamiques des deux modèles.
| On peut effectivement comparer les dynamiques du modèle continu \(y’ =a\,y,+b, \ y(0)=y_0\) et celle du modèle discret \(u(n+1)=(1+a)\,u(n)+b\ , u(0)=u_0\) (supposés adimensionnés) ; les deux modèles sont calculables et il est facile alors de constater que la convergence des deux modèles est bonne quantitativement, du moins en temps fini, si \(|a| \ll 1\). |
L’histoire d’amour s’arrête là car, d’une façon générale, la convergence évoquée plus haut ne se produit pas, pas même sur le seul plan du comportement qualitatif. Les deux types de modèles ont leurs vertus respectives et doivent être utilisés séparément. Signalons que depuis deux décennies, les modèles discrets sont de plus en plus utilisés, poussés par la croissance continue de la capacité de calcul disponible.
Identifications des paramètres
L’identification des paramètres en modélisation est un exemple de problème inverse. Une métaphore un peu simpliste permet de situer cette catégorie de problèmes : « on donne la réponse, trouver la question » , problème dont on perçoit immédiatement la très forte indétermination.
Nous allons examiner un exemple emprunté à la dynamique des populations.
Pour certaines populations d’êtres vivants, il n’y a pas recouvrement des générations (comme dans le cas des lapins de Fibonacci) ; on est en droit de chercher une relation de la forme \(u_{n+1}=f(u_n)\) dans laquelle \(f\) s’appelle la fonction de reproduction. De plus les ressources biotiques sont toujours limitées et constantes et le milieu éventuellement fermé. L’exemple standard est la culture de micro-organismes, à partir d’un ensemencement, par exemple dans une boîte de Petri.
À partir de techniques indirectes de comptage selon un temps caractéristique, les populations sont estimées ; on dispose donc d’une série temporelle \((k, u_k)\). La forme de la courbe des effectifs dévoilée par les données est du type sigmoïde (S allongé) indiquant une croissance faible à partir de l’ensemencement, puis une phase de croissance quasi-linéaire et pour terminer par une phase de ralentissement et quasi-stabilisation .
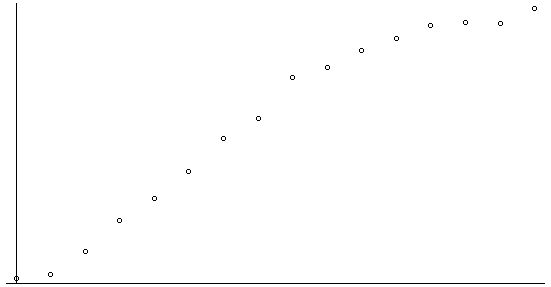
Comment remonter à la fonction de reproduction ? Mathématiquement, le problème est sous-déterminé : il existe une infinité de solutions. On peut faire quelques hypothèses sur \(f\) en plaçant les points \((u_n,\,u_{n+1})\) disponibles : \(f(0)=0\) est raisonnable, \(f\) est strictement croissante, concave et possède un point fixe \(u_{\infty}\). Dans les fonctions usuelles du lycée, deux familles sont candidates : les fonctions homographiques \(x \longmapsto \dfrac{a\,x}{1+b\,x}\) et les fonctions \(x \longmapsto \lambda\,\big(1-\exp(-\mu\,x)\big)\). Voilà un problème d’ajustement sur-déterminé intéressant …
Pierre-François Verhulst a introduit en 1838 son modèle logistique, apportant une réponse analytique à la courbe en S [10] ; ce modèle a été oublié pendant un siècle mais est certainement un des objets mathématiques les plus commentés dans l’histoire récente de l’enseignement.
La solution générale du modèle logistique est de la forme \(x(t)=\dfrac{a}{1+b\,\exp(-c\,t)}\). Il est alors facile de vérifier, pour un choix quelconque d’un temps caractéristique \(\tau\), que \(u_n=x(n\,\tau)\) et \(u_{n+1}=x((n+1)\,\tau)\) sont liés par une relation homographique de la forme \(u_{n+1}=\rho\,\dfrac{u_n}{K+u_n}\). C’est le modèle discret de Verhulst.
En revenant à nos bactéries, le problème est maintenant d’identifier les coefficients \(\rho\) et \(K\) . Une propriété intéressante des récurrences homographiques à points fixes est ici très utile : en posant \(v_n=\dfrac{1}{u_n}\) (ou aussi bien \(v_n=\dfrac{1}{\rho-K-u_n}\)), on obtient une récurrence linéaire et les paramètres peuvent être déterminés par moindres carrés.
Pour conclure
Les IREM et l’APMEP, pour ne citer qu’eux, ont accumulé depuis un demi-siècle une documentation phénoménale sur tous les sujets touchant l’enseignement des mathématiques. La collègue enseignante qui souhaite s’informer pour se former le peut. La vraie difficulté réside sans doute dans le fait que l’institution, qui promeut beaucoup de changements, n’a jamais été en mesure de procéder à une évaluation a priori des besoins (sauf peut-être au moment de la création des IREM) laissant à chaque réforme les enseignantes seules et ni, surtout, à une évaluation a posteriori de l’innovation promue. On peut penser à l’évaluation par compétences qui divise toujours la communauté.
Les didactitiennes ont plutôt supporté – quand ils ne l’ont pas suscité – l’idée de la modélisation comme élément pertinent d’un enseignement des mathématiques répondant à un besoin, mais avec en toile de fond une refonte nécessaire et profonde des curricula voire de l’organisation des enseignements, refonte franchement irréaliste. Même lorsque l’enseignante est maître des contenus et de l’évaluation (par exemple à l’université ou en école d’ingénieurs), une pratique fondée sur des projets d’enquête et de recherche par petits groupes, d’une part demande un travail de préparation déraisonnable et derrière un investissement sincère des étudiantes ; mais cette pratique ne rencontre pas nécessairement l’adhésion de toutes les étudiantes pour diverses raisons dont l’ardeur au travail n’est pas la dernière.
Pour conclure, une pratique raisonnablement authentique d’une activité de modélisation demande bien des prérequis et des conditions qu’il n’est pas simple de rassembler en un lieu donné. La réforme actuelle du lycée a, semble-t-il, crispé les disciplines scientifiques sur la question des postes ce qui ne favorise guère la co-disciplinarité. Voir dans la modélisation une autre appellation de la résolution de (vrais) problèmes est un moyen raisonnable d’y entrer, à petits pas, au fil des occasions, des lectures, des rencontres avec des collègues disposées à partager leurs expériences et en s’appuyant sur les diverses initiatives menées sur tout le territoire.
Annexe : l’analyse dimensionnelle
Nous développons modestement une pratique très répandue dans certains milieux (mécanique des fluides, thermodynamique, résistance des matériaux) et, par contraste, assez peu à l’entrée dans les études supérieurs.
Dans le système international, toutes les grandeurs mesurables peuvent s’exprimer à l’aide de sept grandeurs, dites fondamentales pour cette raison : la masse, la longueur, le temps, la température, l’intensité électrique, la quantité de matière et l’intensité lumineuse. Pour chacune de ces grandeurs, le système définit des unités. Ne conservons que les trois premières (grandeurs fondamentales de la mécanique). On doit rajouter à cette liste les angles plans et solides.
À ces grandeurs on associe — avec James Maxwell — une dimension qui est un symbole reflétant leur nature. Le picomètre, le pouce et l’année-lumière sont des unités distinctes possibles pour la mesure de distances, mais il s’agit à chaque fois d’une longueur. Ces symboles sont M, L et T ; ils peuvent être interprétés comme des réels positifs : si l’unité de grandeur est divisée par X alors la mesure est multipliée par X.
La physique introduit ensuite des grandeurs dérivées comme aire, force, vitesse ou pression.
On s’appuie ensuite sur un axiome fondamental de la physique :
Le rapport de deux valeurs numériques d’une grandeur dérivée quelconque ne dépend pas des unités utilisées pour les grandeurs fondamentales.
On peut alors démontrer que toute unité dérivée (d’une grandeur mécanique) est de la forme \(\textrm{kg}^{\alpha}\textrm{m}^{\beta}\textrm{s}^{\gamma}\textrm{rd}^{\iota}\textrm{sr}^{\phi}\) où les \((\alpha, \beta,\,\gamma,\,\delta,\,\iota,\,\phi)\) sont des réels.
La dimension d’une grandeur physique X est alors le produit des puissances des dimensions des grandeurs fondamentales composant cette grandeur désigné par le symbole \(\textrm{[X]}=\textsf{M}^{\alpha}\textsf{L}^{\beta}\textsf{T}^{\gamma}\)
Angle plan et solide sont donc des grandeurs de dimension 1 comme rapport de longueurs et d’aires.
On dispose d’un calcul sur les dimensions de nature arithmétique :
- si \(\mathrm{X}=\mathrm{Y}\) alors \([\mathrm{X}]=[\mathrm{Y}]\) et aussi \([\mathrm{X} \pm\mathrm{Y}]=[\mathrm{X}]\) ;
- \([\mathrm{X} \mathrm{Y}]=[\mathrm{X}][\mathrm{Y}]\) ;
- \(\left[\dfrac{\textrm{X}}{\textrm{Y}}\right]=[\textrm{X}][\textrm{Y}]^{-1}\) ;
- \([\textrm{X}^{\alpha}]=[\textrm{X}]^{\alpha}\) ;
- \(\displaystyle\left[\int_{X_0}^Xf(\xi) \text{d}\xi\right]=[\mathrm{X}] [f]\) ;
- \(\left[\dfrac{\textrm{d X}}{\textrm{d Y}}\right]=[\textrm{X}][\textrm{Y}]^{-1}\) ; \(\left[\dfrac{ \text{d}^2\textrm{X}}{ \textrm{d Y}^2}\right]=[\textrm{X}][\textrm{Y}]^{-2}\)
La première égalité est le principe d’homogénéité dimensionnelle. Cette égalité peut être déduite du principe d’indépendance des lois physiques du système d’unités utilisé. Les règles sur la dérivation et l’intégration se comprennent bien si on se souvient qu’une dérivée est une limite de quotients et une intégrale une limite de somme de produits.
Les relations entre les grandeurs constituant le modèle, qu’elles soient différentielles ou non, doivent satisfaire à la règle d’homogénéité. Inversement toute relation entre grandeurs permet de former ce qu’on appelle l’équation aux dimensions de la relation.
On retiendra aussi que :
- les arguments des fonctions transcendantes (\(\sin\), \(\ln\), \(\exp\), etc.) et, plus généralement, toutes les fonctions admettant un développement en série entière, et les valeurs d’icelles sont nécessairement sans dimension8 ;
- les exposants des fonctions puissances (comme le \(\gamma\) dans \(p\,v^{\gamma}=\textrm{ Cste}\)) sont sans dimension ;
- toutes les constantes mathématiques sont sans dimensions : \(\sqrt{2}\), \(\text{e}\), \(\text{i}\), \(\pi\)…
Le théorème central de l’analyse dimensionnelle est le théorème Pi.
Le comportement d’un système tel qu’il est décrit par une relation (différentielle ou non) entre des grandeurs ne peut dépendre de la valeur d’un paramètre dimensionnel, sinon un changement d’unités induirait un changement de comportement. Pour garantir cette indépendance, il suffit que la relation modèle ne fasse intervenir que des produits9 adimensionnels. En réalité, on peut démontrer que la condition est nécessaire, c’est le théorème Pi10 :
Toute équation homogène du point de vue des dimensions peut être transformée en une relation entre les membres d’une famille de produits adimensionnels. Si le nombre de paramètres dimensionnels de l’équation initiale est \(n\) et si ces paramètres font intervenir \(N \leqslant n\) dimensions fondamentales, alors le nombre de produits adimensionnels est égal à \(n-N\).
Un exemple s’impose : le tube absolu porte sur la période du pendule pensant. Un pendule simple de masse \(m\), de longueur \(\ell\), oscille librement dans le champ de pesanteur supposé constant. On s’intéresse à sa période \(T\). Retenons comme paramètres pertinents, \(\alpha\) angle maximal par rapport à la position d’équilibre, \(g\) (accélération de la pesanteur), \(m\), \(\ell\) et \(T\). On postule donc l’existence d’une relation \(T=f(\alpha,\,m,\,\ell,\,T)\).
Les dimensions sont : \[[\alpha]=1,\qquad [T]=\textsf{T},\qquad [g]=\textsf{L}\textsf{T}^{-2},\qquad [m]=\textsf{M},\qquad [\ell]=\textsf{L}\]
Cherchons les produits adimensionnels : il y a 4 grandeurs s’exprimant en fonction de 3 grandeurs indépendantes, donc un seul produit adimensionnel ; on a : \[T^{\alpha}g^{\beta}m^{\gamma}\ell^{\delta}=1\ \leftrightarrow \ \begin{cases} \alpha-2\,\beta=0 \\ \beta+\delta=0 \\ \gamma=0 \end{cases}\ \leftrightarrow\ \begin{cases} \alpha=2\,\beta \\ \gamma=0 \\ \delta=-\beta \end{cases}\] donc le seul produit adimensionnel est \(T^2\displaystyle \dfrac {g}{\ell}\) ce qui était évident a priori. Et la seule relation homogène possible est \(T^2 \dfrac {g}{\ell}=g(\alpha)\), soit \(T=h(\alpha)\sqrt{\dfrac {\ell}{g}}\). L’analyse dimensionnelle ne peut dire plus. Mais on peut faire des mesures expérimentales.
Adimensionnement
Une fois qu’on dispose d’un modèle, il s’agit de le faire parler. Plusieurs types de réponses sont envisageables :
- les réponses numériques fournies aujourd’hui par des logiciels de calcul sous forme de courbes, dessin 2D ou 3D, ou tableaux ; ces réponses numériques sont des suites convergentes vers des solutions du deuxième type ;
- les réponses exactes dites « analytiques » en acceptant des solutions définies par des séries, des intégrales, voire implicitement ;
- les réponses analytiques approchées qui sont des solutions exactes d’équations approchées, à l’image du paradigme \(\theta=\theta_0\cos(\omega\,t)\) solution exacte de l’équation \(\ddot{\theta}+\omega^2\,\theta=0\), elle-même équation approchée de l’équation du pendule mathématique \(\ddot{\theta}+\omega^2\,\sin\theta=0\).
Pour obtenir une bonne équation approchée, une méthode est de s’appuyer sur la taille de certains termes afin de négliger les termes « petits » . Toute la question est de donner un sens objectif aux termes « petits » et « grands » .
Il est bien évident qu’une grandeur n’est pas intrinsèquement grande ou petite. Une vitesse de 1 mètre par seconde est insignifiante pour une Maranello et colossale pour un Helix aspersa. Ce qui fait sens c’est le nombre qui mesure le rapport à une grandeur de référence. Adimensionner un modèle, c’est choisir des grandeurs de référence qui sont prises comme unité pour reformuler le modèle de façon à n’avoir plus que des relations entre grandeurs sans dimension.
Le choix de ces grandeurs de référence n’est en général pas unique et il y a dans ce cas plusieurs façons d’adimensionner un modèle ; mais elles ne sont pas toutes physiquement pertinentes. Le choix des bonnes grandeurs caractéristiques relève complètement d’une bonne maîtrise de la physique du système étudié.
Prenons l’exemple de la radioactivité de modèle \[\dfrac{\text{d}N}{\text{d} t}=-k\,N \qquad N(0)=N_0\] dans laquelle \(N(t)\) est le nombre de radionucléides d’un type donné à l’instant \(t\). Aussi bien cela peut être une masse.
L’analyse dimensionnelle donne : \([ N ]= [N_0]= \textsf{M}\) et \([k]=\textsf{T}^{-1}\).
Le choix est ici évident ; on prend \(N_0\) et \(\dfrac{1}{k}\) comme grandeurs caractéristiques ; avec \(t^{\ast}=k\,t\) et \(N^{\ast}=\dfrac{N}{N_0}\), le modèle adimensionné est \[\dfrac{\text{d}N^{\ast}}{\text{d}t^{\ast}}=-N^{\ast} \qquad N^{\ast}(0)=1\] de solution \(N^{\ast}=\exp(-t^{\ast})\), relation entre nombres purs mais qui restent perçus comme des grandeurs avec unités particulières.
Grandeurs caractéristiques
Donnons deux exemples simples (et très classiques) :
- Une masse \(m\) est lancée à la vitesse \(v_0\) sur un axe horizontal. Elle subit une force de freinage \(F=-f\,v\) proportionnelle à sa vitesse \(v\). Sans écrire aucune équation pour modéliser le problème, l’analyse dimensionnelle donne : \[[m]=\textsf{M},\qquad [v_0]=\textsf{L}\textsf{T}^{-1},\qquad [f]=\textsf{M}\textsf{T}^{-1}\] On voit immédiatement qu’on ne peut construire avec ces dimensions qu’un seul temps, une seule longueur, une seule accélération : \[\tau=\displaystyle \dfrac {m}{f},\qquad \xi=\displaystyle \dfrac {m\,v_0}{f},\qquad \gamma=\displaystyle \dfrac {f\,v_0}{m}\] Si le recensement a priori des variables pertinentes pour le problème étudié est correct, ces grandeurs déterminées de façon unique ont raisonnablement un sens physique ; on peut ainsi penser que \(\tau\) est un temps (une durée) caractéristique au sens où au bout d’un temps \(\tau\) le système aura évolué de manière significative — ici sa vitesse aura diminué de manière significative — et qu’au bout d’un temps grand devant \(\tau\) sa vitesse sera faible devant sa vitesse initiale ; on peut penser que \(\xi\) sera une distance de freinage caractéristique. Enfin \(\gamma=\dfrac{\xi}{\tau^2}\). Un ingénieur dira sans hésiter que le freinage dure un temps \(\tau\), sur une distance \(\xi\) avec une décélération \(-\gamma\).
- Abordons le problème du parachutiste ; une masse \(m\) (initialement au repos) tombe verticalement sous l’action de la pesanteur ; on suppose que la résistance de l’air est modélisable par une force de freinage \(\vec{F}=-k\,v\,\vec{v}\). En supposant que les trois paramètres \(g\), \(k\), \(m\) sont bien les seuls paramètres pertinents dans ce problème, on a : \[[m]=\textsf{M},\qquad [g]=\textsf{L}\textsf{T}^{-2},\qquad [k] = \textsf{M}\textsf{L}^{-1}\] Sont possibles une seule longueur : \(\xi=\displaystyle \dfrac {m}{k}\), un seul temps : \(\tau=\sqrt{\displaystyle \dfrac {m}{k\,g}}\), et une seule vitesse : \(\nu=\sqrt{\displaystyle \dfrac {m\,g}{k}}\). L’interprétation physique de \(\nu\) n’est pas possible sur la base de la seule analyse dimensionnelle (vitesse limite) ; mais on peut dire qu’elle est atteinte en un temps caractéristique \(\tau\) sur une distance de chute \(\xi\). Si on introduit le modèle différentiel (avec des hypothèses non explicitées mais assez …explicites) \[-\ddot{x}=g – \dfrac{k}{m}\,\dot{x}^2 \quad x(0) = H \quad \dot{x}(0)=0\] Pour la vitesse \(v=\dot{x}\) le modèle est \(-\dot{v}=g-\dfrac{k}{m}v^2 \quad v(0)=0\) indépendant de \(H\).
| Avec \(t^{\ast}=\dfrac{1}{\tau}\,t\) et \(v^{\ast}=\dfrac{1}{\nu}\,v\), le modèle adimensionné est \(\displaystyle \dot{v}^{\ast}={v^{\ast}}^2-1 \quad v^{\ast}(0)=0\) ; le lecteur appréciera au passage l’efficacité des notations différentielles ; il suffit de tenter le changement de variables avec le théorème \( (g \circ f)’ \) pour y renoncer définitivement. La solution (éventuellement fournie par un logiciel de calcul formel) est simplement : \(v^{\ast}=-\tanh(t^{\ast})\). \(v^{\ast}=-1\) soit \(v=\nu\) est donc bien solution asymptotique (ce que l’on peut obtenir sans résoudre l’équation). |
Références
- Michel Soufflet : Les mathématiques de tous les jours. Vuibert, 2005.
- Yves Chevallard : La calculatrice, ce bon objet. 2006. Disponible sur yves.chevallard.free.fr.
- Denise Grenier, Marc Legrand et Françoise Richard : Un exemple de modélisation. Cahier de didactique, N. 22, 1986. Disponible sur irem.u-paris.fr.
- Philippe Dutarte : Présenter aux futur(e)s professeur(e)s une image positive de la statistique et de ses enjeux citoyens. 2007. Disponible sur Publimath.
- Léo Gerville-Réache et Vincent Couallier : L’enseignement des affaires woburn et castaneda. 2014. Disponible sur hal.archives-ouvertes.fr.
- Commission Inter-Irem Statistiques et Probabilités : Autour de la modélisation en probabilités. PUFC,2001. Disponible sur Publimath.
- Bernard Walliser : Systèmes et modèles. Seuil, 1977.
- Giorgio Israel : La mathématisation du réel. Seuil, 1996.
- Richard Haberman : Mathematical Models : Mechanical Vibrations, Population Dynamics, and Traffic Flow. SIAM, 1998. Remarquable à tous points de vue.
- Bernard Delmas : Pierre-françois Verhulst et la loi logistique de la population. Mathématiques et Sciences humaines, N. 167, 2004. Disponible sur www.numdam.org.
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
François Boucher, à la retraite depuis quelques années, continue de s’intéresser aux mathématiques et à leur enseignement.
- On pourra consulter l’article d’Aurélien Alvarez.
- Signalons que l’ouvrage Mathématiques de tous les jours mérite vraiment de figurer dans toutes les bibliothèques.
- Un par mois, avec 5 minutes par cours pour qu’un élève présente l’avancement de sa recherche. Il s’agissait d’une classe un peu spéciale, préparant à une Première S en deux ans.
- http ://clea-astro.eu/archives/web/.
- Cela ne vous rappelle rien ?
- Variation brutale de l’accélération.
- Il n’y a pas de migration…
- Le cas des lignes trigonométriques peut troubler ; conventionnellement, si \(x\) dénote la mesure d’un angle dans \(\cos(x)\), il est nécessairement exprimé en radians ; sinon, un facteur de changement d’unité est impératif, comme \(\dfrac{\pi}{180}\) dans le cas d’un angle exprimé en degrés. Mais on trouve un peu partout des écritures comme \(\cos(20°)\).
- Comprendre que les quotients sont des produits.
- Appelé théorème de Buckingham dans le monde anglo-saxon et théorème de Vaschy en France.


Une réflexion sur « Petite enquête sur … la modélisation – Complément numérique »
Les commentaires sont fermés.