Agrandissement, réduction. . . , rotation
La multiplication comme agrandissement–réduction est une mine d’activités intéressantes. Christian Mercat nous présente une approche particulièrement graphique, visitant l’histoire avec la perspective et ses machines à dessiner vues comme des tables de multiplications de grandeurs.
Christian Mercat
© APMEP Mars 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Le puzzle de Brousseau [2] est une situation fondamentale pour comprendre que l’agrandissement ne relève pas du champ additif sur les longueurs mais du champ multiplicatif. C’est par la complémentarité ou non avec les autres pièces, production des autres élèves, que la préservation des angles, la conformité des pièces, s’installe comme le critère principal de validation et la proportionnalité des longueurs comme l’outil de résolution du problème.
Pour autant, la multiplication peine souvent à sortir de l’addition itérée et la proportionnalité est ensuite rarement revisitée d’un point de vue graphique.
La réintroduction en 2016 de l’homothétie dans les programmes est l’occasion de mieux comprendre le théorème de Thalès comme une version géométrique de la proportionnalité, et de donner du sens à la multiplication par des décimaux, y compris négatifs.
Des notions subtiles sont pourtant plus claires sur un dessin que sur des tableaux de nombres : les rapports internes d’une figure, celui du bras par la taille d’une figurine par exemple, sont conservés dans un agrandissement ou une réduction. Le rapport externe entre le grand et le petit, le coefficient de proportionnalité, est le même pour chaque partie de la figurine, le rapport de la longueur du grand bras par celle du petit bras est le même que celui de la grande tête par la petite, (Figure 1).
Figure 1. Machine à perspective de Dürer (circa 1600).↩
La formalisation des règles du dessin en perspective est une étape intellectuelle fondamentale de la Renaissance. On l’a beaucoup dit, c’est une révolution artistique autorisée par une révolution philosophique et religieuse, permettant en retour une révolution scientifique. Là où l’artiste du Moyen-Âge ne peut pas peindre le Christ plus petit que les apôtres qui sont devant Lui, ou l’échiquier auquel jouent le seigneur et sa dame autrement qu’avec des carrés, le peintre de la Renaissance entend peindre ce qui est plutôt que ce qui est su et accepté. C’est dire que « mon point de vue vaut bien celui du Pape ». S’ensuit l’importance de la raison, de la mise en rapport des effets et des causes, graphique tout d’abord sur la toile, philosophique et scientifique dans les essais et les expériences. Les premiers scientifiques sont en effet des artistes qui tentent d’utiliser l’objectif de leur œil pour décrire le monde tel qu’il est et tenter de le comprendre objectivement.
Des machines sont utilisées pour faciliter le travail des artistes. Albrecht Dürer par exemple décrit ses méthodes dans ses gravures. L’œil de l’artiste est objectivé par un point, tenu à une certaine distance d’un plan de projection, sur lequel se projette l’image d’un objet placé au-delà du plan, à une certaine distance. Une autre machine, déjà connue des grecs antiques, est la chambre obscure, où l’objectif est un orifice dans une cloison séparant le monde extérieur éclairé de la chambre noire sur le mur de laquelle se projette à l’envers l’objet à peindre (Figure 2).
Ces machines peuvent être comprises comme des tables de multiplication. En effet, fixer le rapport (algébrique) des distances de l’objet à l’objectif d’une part et de l’objectif au plan de projection d’autre part, c’est fixer un coefficient d’agrandissement ou (plutôt) de réduction, comme dans l’illustration ci-dessous.
L’agrandissement apparaît avec les lanternes magiques et les ombres chinoises et se démocratise avec l’invention des frères Lumière, le cinéma : l’objet est la pellicule et c’est bien agrandie qu’on la voit sur l’écran de projection. Avant d’agir sur des nombres, la multiplication agit sur des longueurs.
Si on veut vraiment des nombres, on n’a qu’à dessiner une règle graduée, ce qui permet d’apprécier que les nombres opèrent les uns sur les autres, par addition et soustraction, c’est la translation de la règle, et par multiplication et division comme nous allons le voir.
Prenons une règle moderne, mesurant des longueurs algébriques, non pas comme les règles carrées en métal avec une extrémité où commencent les graduations mais faisant figurer un zéro, et des longueurs positives d’un côté, des longueurs négatives de l’autre, repérant des points sur la droite graduée et non sur une demi-droite. Tenons la verticalement pour mesurer l’altitude et la profondeur par rapport à un niveau de référence (Figure 3).
L’image sur la machine à dessiner, est celle d’une règle, réduite dans une autre unité. Le rapport externe (défini ci-dessus), peut se mesurer : l’unité est envoyée sur une autre longueur (algébrique) q ; on place une deuxième règle graduée, dans l’unité de départ, le long de l’image en faisant coïncider les zéros. La loupe (en rouge) permet de voir que le chiffre 1 des graduations sur l’image est associé à ce nombre q, que l’on lit sur cette deuxième règle, -0,7 dans l’exemple.
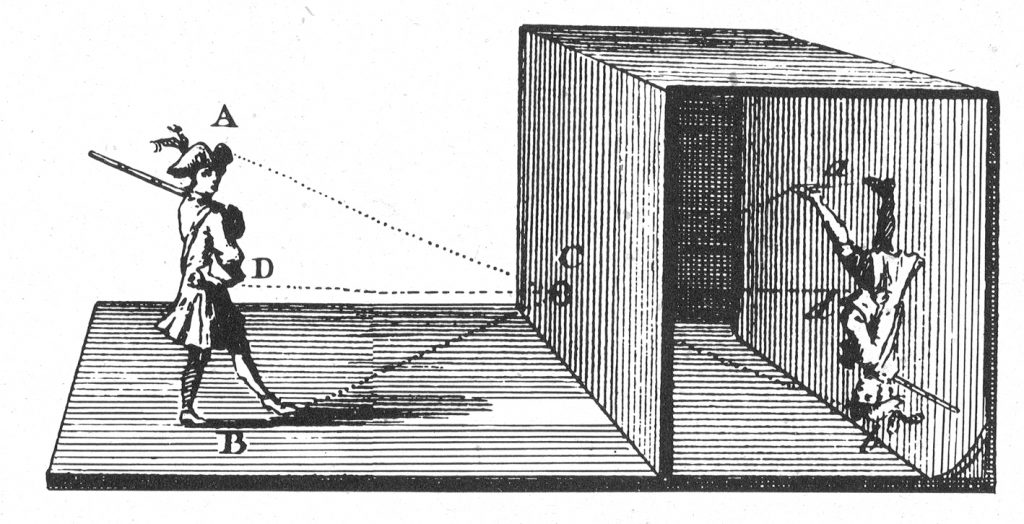
Figure 2. Chambre obscure dans l’encyclopédie de Diderot et d’Alembert (1772).↩
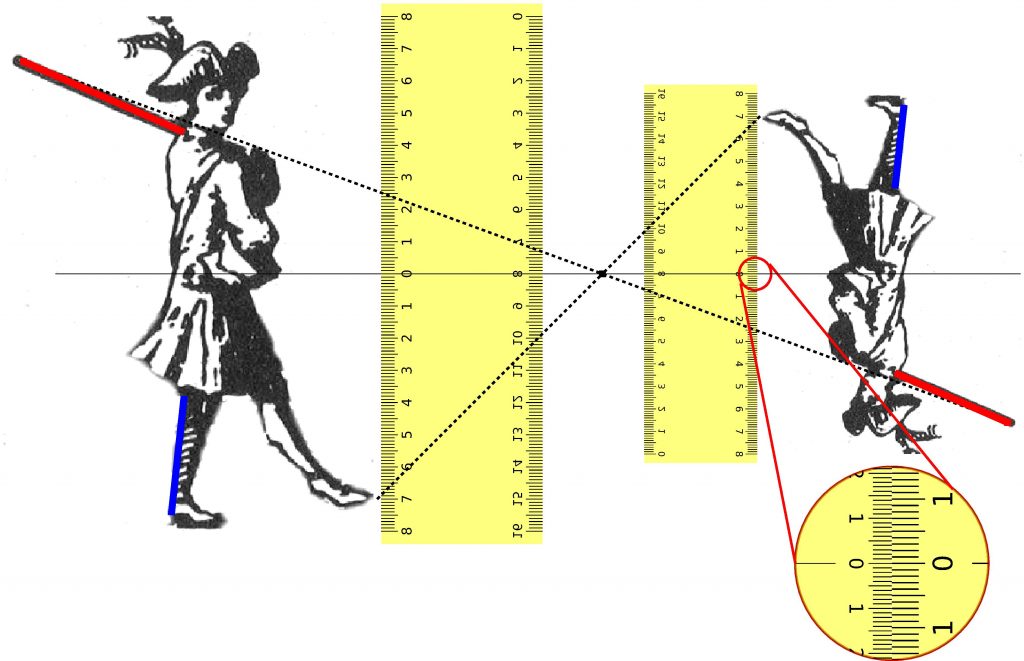
Figure 3. Multiplication par -0,7. Les rapports internes (rouge/bleu) sont conservés, le rapport externe petit/grand également.↩
On peut, de la même manière, lire ce que vaut le produit de n’importe quel autre nombre de départ par ce même rapport q. Multiplier par q est ainsi vu comme l’agrandissement (ou la réduction) agissant sur la règle de départ, le zéro étant fixé, jusqu’à ce que la graduation 1 soit envoyée sur q, le reste de la règle suivant proportionnellement.
La configuration de la chambre obscure est ici importante car elle permet de donner un sens géométrique à un calcul algébrique tel que $$-0,7 \times (-1,4) = 0,9$$
en lisant que -1,4 sur la règle modifiée se retrouve à la cote +0,9.
Les machines plus classiques de Dürer sont aussi importantes pour déstabiliser la conception de la multiplication comme seul agrandissement car si elles multiplient par des nombres réels, ils sont souvent plus petits que 1, et on peut les approcher par les décimaux de la règle graduée, donnant à voir de manière assez naturelle une multiplication qui pourtant réduit.
Comment visualiser les propriétés de la multiplication ? La droite des réels est trop mince pour voir les agrandissements et il faut s’installer dans le plan pour en apprécier pleinement les effets et les propriétés. Par exemple la commutativité de la multiplication comme addition itérée ne se comprend facilement qu’en rangeant par lignes et par colonnes.
Les gobelets servent à rassembler, il y a autant de pastilles dans cinq gobelets contenant 3 pastilles que dans trois gobelets contenant cinq pastilles et pour le comprendre, il faut les arranger en rectangle. Si on dessine simplement le rectangle, on ne comprend pas qu’il y a un problème pour l’enfant. Il est nécessaire de réorganiser la situation où les lignes et les colonnes du rectangle ne sont pas naturellement étiquetées par les mêmes qualités ; abstraire ces qualités est un passage obligé de la construction du nombre, il y a en tout 15 pastilles.

Figure 4. Une évidence manipulatoire invisible sur la droite.
Plus généralement, depuis les Grecs, on interprète le produit de deux longueurs comme la surface d’un rectangle. La symétrie axiale dans le plan est alors la clef de la commutativité. On peut se ramener à des nombres en choisissant une unité qui permet alors de ramener une aire à la longueur d’un rectangle de largeur unité de même surface (Figure 5).
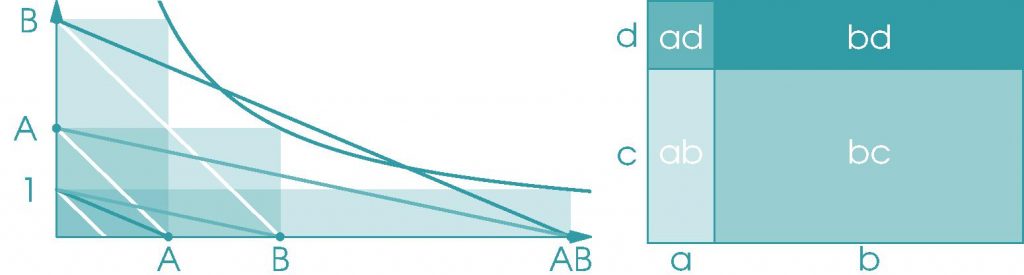
Figure 5. La commutativité de la multiplication entre deux longueurs, son interprétation comme une aire étant donnée une unité. Et la double distributivité.↩
Ces propriétés classiques (sans pour autant être simples ou intuitives) de l’addition itérée, comme l’associativité, la commutativité ou la distributivité sur l’addition, empruntent souvent au registre graphique pour un appui intuitif avec des arrangements spatiaux de grandeurs ou collections.
Ces propriétés prennent un sens tout autre dans l’interprétation de la multiplication comme opération d’agrandissement-réduction et ne gagne vraiment en clarté et en évidence que quand les opérandes sont eux-même non pas des points de la droite mais des points du plan, des nombres complexes.
Comment voit-on la multiplication par les nombres complexes ?
Nous procédons de la même manière qu’en agrandissant ou réduisant une règle mais en agissant sur tout le plan, emmenant avec lui le quadrillage des points de coordonnées entières. Cette opération peut se faire à l’aide d’un antique rétro-projecteur projetant un transparent quadrillé sur un tableau quadrillé (Figure 6).
Par exemple, multiplions par \(q=0,5+\mathrm{i}\).
Visualisons où se trouve le nombre \(q=0,5+\mathrm{i}\) dans le plan. On amène alors la graduation 1 de l’axe horizontal (le nombre 1) sur ce nombre en déformant le quadrillage (bleu) des entiers suivant la similitude de centre O associée.
Sur les graduations de ce nouveau quadrillage (bleu), on peut lire le point d’affixe z, par exemple \(z=1-2\mathrm{i}\). L’affixe de ce point dans le quadrillage initial est celle du complexe q×z ! Par exemple, géométriquement, le produit de \(0,5+\mathrm{i}\) par \(1-2\mathrm{i}\) nous ramène sur la droite des réels, on lit $$(0,5+\mathrm{i})\times(1-2\mathrm{i})=2,5.$$
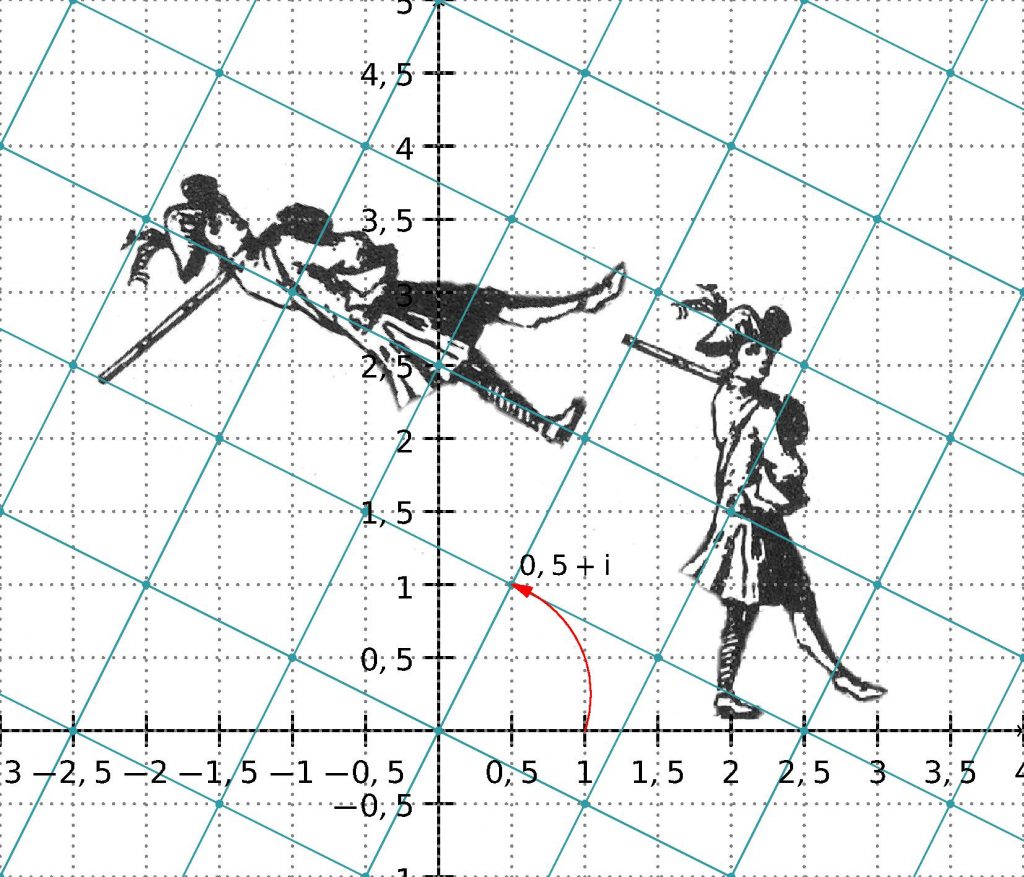
Figure 6. Multiplication par \(0,5 + \mathrm{i}\).↩
Je vous laisse vérifier que
$$(0,5+\mathrm{i})\times(1+\mathrm{i})=-0,5+1,5\mathrm{i}$$
ou encore que \((0,5+\mathrm{i})\times(2-2\mathrm{i})=3+\mathrm{i}\) et également que la multiplication d’un nombre par son conjugué est réelle.
Une animation sur GeoGebra permet de jouer avec d’autres valeurs de z et q.
Cette compréhension géométrique de la multiplication donne du sens à la règle des signes des réels qui sinon paraît surtout conventionnelle. On peut supposer que la multiplication des réels est épistémologiquement plus difficile que la multiplication des complexes : à la fin du XVIIIe, Gauss, Euler et consorts n’avaient pas de problèmes à s’entendre sur la valeur d’une expression comportant des nombres complexes mais il a fallu attendre 1870 pour que tous les mathématiciens s’accordent sur l’enseignement de l’évaluation des expressions réels comprenant des négatifs ! Et nous n’avons pas fini d’en parler encore aujourd’hui.

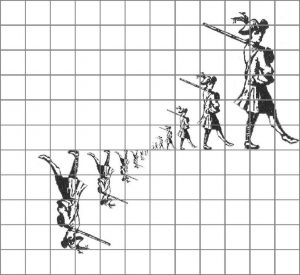
Figure 7. Illustration des suites de raison \(\dfrac{3}{4}\) et \(-\dfrac{3}{4}\cdotp\)
L’itération de la multiplication donne naissance à des suites fondamentales, les suites géométriques. Mais elles sont rarement présentées de manière géométrique !
Pourtant elles rappellent les alignements vus en perspective.
Les suites géométriques apparaissent également dans la disposition des frettes des instruments de musique. Trouver la raison de la suite géométrique qui amène une frette sur la suivante est une activité simple et intéressante (Figure 9).
La somme des termes d’une suite géométrique sort aussi de l’incantation magique algébrique pour devenir compréhensible graphiquement. Considérons une suite de carrés. Comment pouvons-nous nous rendre compte du fait qu’ils sont en raison constante, qu’ils forment une suite géométrique ? Simplement en les disposant les uns contre les autres, alignés sur leur base (Figure 8).
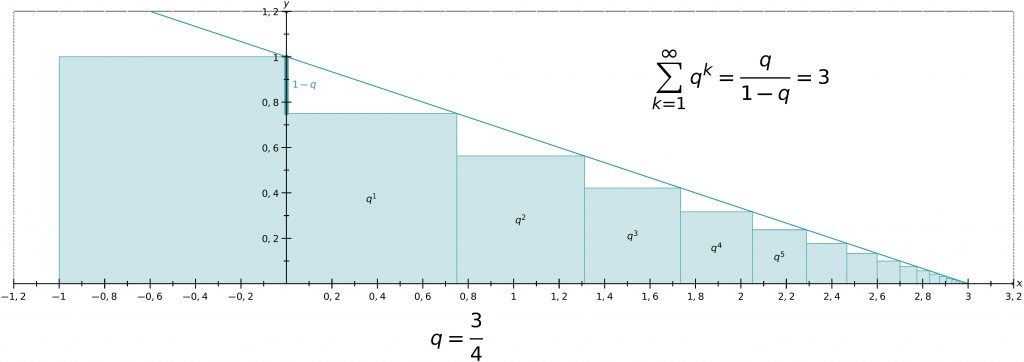
Figure 8. La somme des termes de la suite géométrique de raison \(\dfrac{3}{4}\) et de premier terme \(\dfrac{3}{4}\) vaut 3.↩
Si un carré est au suivant dans une raison constante q, leurs coins sont alors également alignés, selon une pente donnée, valant \(\frac{1-q}{q}\) et la somme de tous les termes est finie si q < 1, c’est la longueur où la droite passant par les coins rencontre l’axe horizontal. Si on tient à passer aux nombres, on choisit une unité et on peut mesurer cette longueur.
Les suites géométriques complexes sont encore plus belles que les suites géométriques réelles, et se rencontrent dans de nombreuses occasions, en particulier dans la nature, où des processus autosimilaires répliquent une logique de multiplication, du niveau cellulaire jusqu’à l’organisme entier.
On s’amusera à trouver la raison de la suite géométrique derrière la spirale d’une fleur de tournesol, d’un chou, ou d’une ammonite (Figure 10).
On s’apercevra d’ailleurs que la raison d’or ϕ n’est pas aussi omniprésente qu’on peut le lire partout sur l’internet !
Grâce aux suites géométriques dont on sait facilement calculer les limites, encadrer une suite par deux suites géométriques est un outil essentiel pour la preuve de la convergence de la suite.

Figure 9. La racine douzième d’un demi est la raison de la suite géométrique définissant la position des frettes d’un instrument dodécaphonique.↩
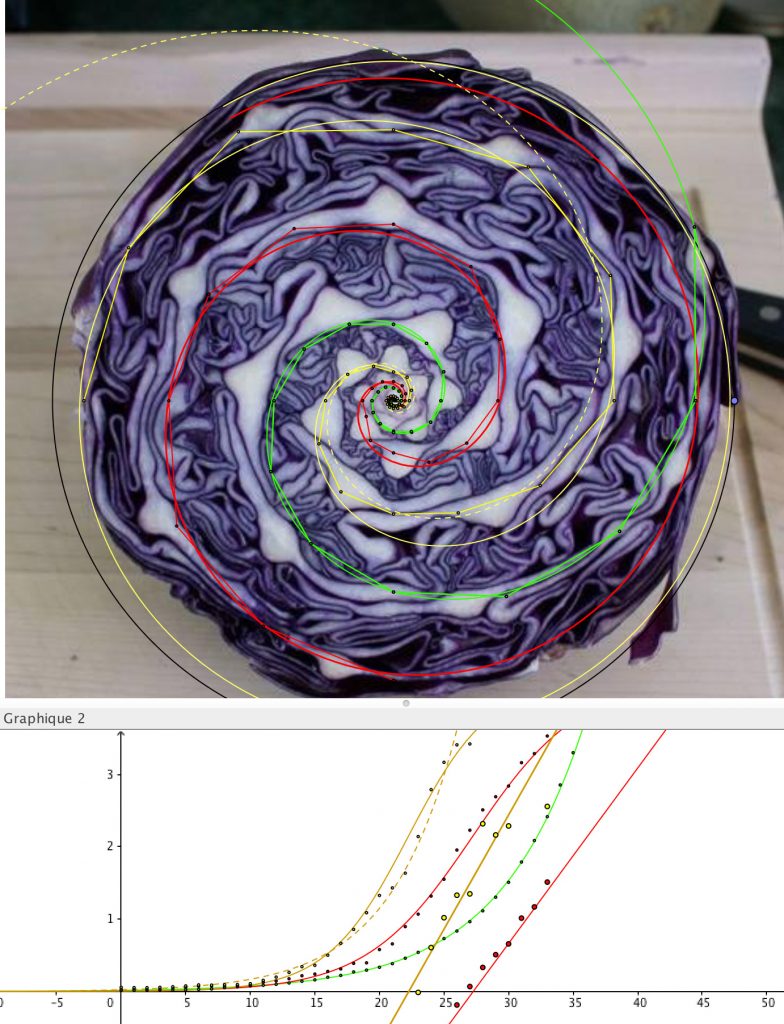
Figure 10. Les points apparaissant sur une spirale sont extrapolés par une loi de puissance, sur un certain intervalle, la modélisation par une spirale logarithmique est adéquate. ↩
Enfin, mon dernier point sera sur les fonctions analytiques où la dérivée comme taux d’accroissement est plus claire dans le plan que pour les fonctions réelles.
Le premier constat qui souligne la plus grande facilité à comprendre les objets du plan que de la ligne est que tout un chacun sait lire le graphique de la Figure 12 .
Les maxima sont clairs, des précipitations plus de 3 fois supérieures à la normale dans la région de Montpellier, une grande sécheresse dans le grand Est (moitié moins à Nancy-Metz) et surtout (3 fois moins d’eau) en Bourgogne. C’est pourtant le graphe d’une fonction du plan dans les réels ! Tout le monde comprend qu’on colorie le point z de la couleur de la valeur de la fonction en ce point, f(z) qui prend ses valeurs de 20 rouge vif s’il a fait très sec à 500 bleu roi s’il n’a fait que pleuvoir.
De la même manière, on peut visualiser une fonction analytique du plan en peignant le plan non pas comme sur la ligne de rouge à bleu mais par une image, par exemple celle prise par la caméra d’un ordinateur, qu’on taille en un carré dont on pave le plan de manière périodique. À chaque nombre complexe correspond ainsi un pixel de l’image
Alors, toute fonction à valeur complexe peut se visualiser en coloriant chaque point z de la couleur du pixel de l’image associé au point f(z).
Les fonctions les plus simples sont les similitudes, composées d’une translation, d’une homothétie et d’une rotation, c’est-à-dire de la forme z↦az+b avec a et b des points complexes. La dérivée de cette fonction est constante, c’est-à-dire que tous les points sont tournés et agrandis/réduits de la même manière. De plus, comme c’est le graphe d’une fonction, si le taux de variation est grand, le zoom de l’image est faible et au contraire, si le taux de variation est faible, un pixel va s’étaler sur toute une zone, la dérivée est faible, jusqu’à une valeur constante, tous les points ont la même couleur (Figure 11).

Figure 11. Caméra conforme. Il est important de jouer avec si on veut avoir une petite idée : ici.↩
Les fonctions usuelles, par exemple (presque) toutes celles disponibles sur une calculatrice, exp, cos, racine carrée, tan, l’inverse, le carré, le cube… sont analytiques, c’est-à-dire qu’elles peuvent s’étendre à tout le plan complexe et sont localement une similitude : f(z+a) =f(a) +zfʹ(a) +o(z)
Le taux d’accroissement en un point a est la dérivé fʹ(a). Ainsi, quand on visualise une fonction analytique, on voit dans le même regard, la valeur et la dérivée de la fonction en un point : La valeur est donnée par la couleur du point, et la valeur du taux de variation comme pour une similitude, par la magnitude du zoom. On voit également l’argument par l’angle que fait l’image avec la verticale : si l’image reste verticale, la dérivée est réelle positive, si on est « la tête en bas », la dérivée est réelle négative.
L’utilisation de cet outil dans la classe est principalement récréative mais elle peut faire exister l’idée que la dérivée est un taux de variation, qui localement agit comme un facteur multiplicatif des variations de l’image par aux variations de l’antécédent.
En conclusion de mon plaidoyer pour une interprétation géométrique de la multiplication, tout en espérant avoir montré la puissance de la géométrie, je ne voudrais pas en faire une ennemie de l’algèbre ou de la technique calculatoire. Savoir manipuler des expressions, connaître ses tables de multiplication, calculer de tête, poser des multiplications à plusieurs chiffres, dérouler l’algorithme de report de la retenue et toutes ces techniques de calcul algébrique ou posé sont nécessaires pour une aisance dans les manipulations. Il ne faut pas être bloqué par ces techniques.
Cependant, il ne faut pas penser que l’apprentissage ou même l’excellence de ces techniques permet l’accès à la compréhension de ce qu’elles représentent. Aussi je suggère d’illustrer, quand c’est possible (et ça l’est souvent), un problème algébrique ou calculatoire d’un petit dessin, d’une interprétation géométrique qui donne du sens à la multiplication.
Références
-
Anne Boyé. « Quelques éléments d’histoire des nombres négatifs ». In : sous la dir. de Penélope Proyecto. projet Comenius « Enseignements interdisciplinaires européens de l’histoire des sciences au lycée », 2002.
-
Guy Brousseau. « Problèmes de didactique des décimaux ». In : Recherches en Didactique des Mathématiques 2.1 (1981).↩
-
Favennec Denis et Emmanuel Riboulet-Deyris. Douce perspective, une histoire de science et d’art. Paris : Ellipses, 2007.
-
Christian Mercat. « La diffusion, un lieu pour une mathématique plus humaine ? Espace Mathématique Francophone 2015 ». In : Actes EMF2015 pluralités culturelles et universalité des mathématiques, enjeux et perspectives pour leur enseignement et leur apprentissage, Projet spécial n° 2 : vulgarisation des mathématiques. Alger, oct. 2015.
-
Suite géométrique. 2016.
Christian Mercat est professeur des universités en mathématiques à l’ÉSPÉ de Lyon et directeur de l’IREM de Lyon.
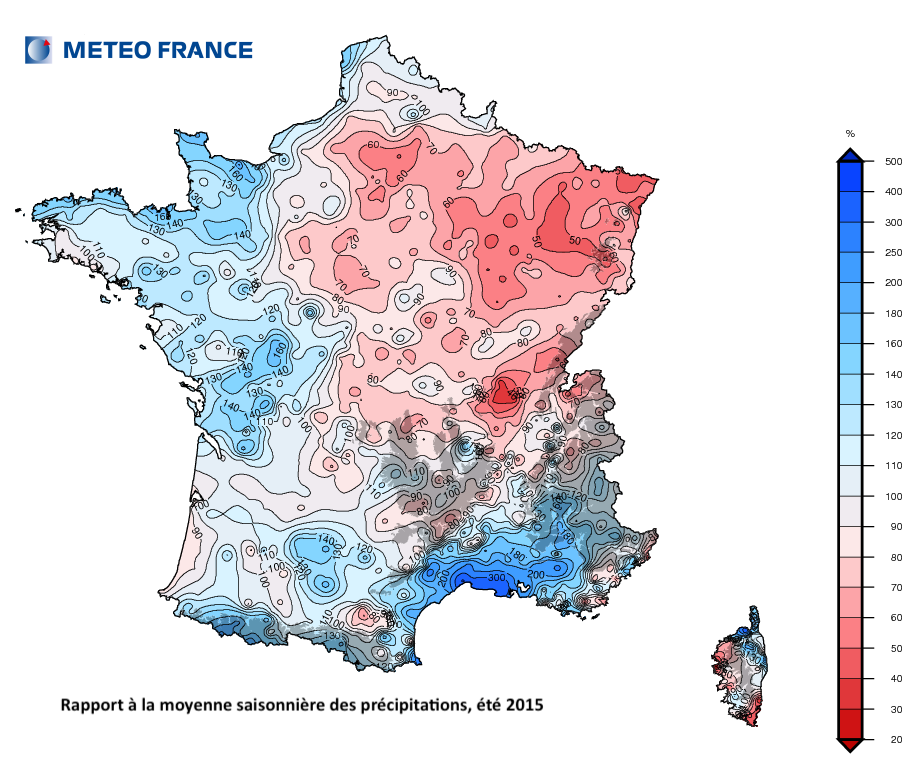
Figure 12. Graphique de rapport à la moyenne saisonnière des précipitations. ↩
