D’une observation de Fermat à un moment de calcul

Cet article propose une réflexion à partir d’un texte de Fermat dans lequel il s’exprime en termes de nombres figurés. Ce texte énonce une propriété numérique assez élaborée, sans autre développement, dans une période où l’algèbre se déploie. De là, un point de départ pour tenter de situer cet écrit, entre tradition et modernité.

Jean Aymès

© APMEP Septembre 2021

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Précisons le substrat mathématique du texte et explorons son contexte, ce qu’il peut signifier.

Une tradition bimillénaire : des figures pour représenter des nombres

Le langage géométrique présent dans ces textes décrit un calcul ; ces mots polygone, triangle, désignent bien des nombres, des nombres figurés, un ancien héritage. Il nous en reste des traces aujourd’hui dans le lexique mathématique, avec carré pour le produit d’un nombre par lui-même, une organisation de points en carré³. Pour le cube, il en est de même.

Sous cette forme, ceci nous vient au moins de l’époque de Pythagore. Des propriétés abstraites des nombres entiers sont étudiées, c’est l’arithmétique pythagoricienne avec des nombres triangulaires, des nombres carrés, etc. Ce lien entre géométrie et arithmétique n’est pas sans force pour exprimer des propriétés des nombres.

Cette figuration (figure 1) en équerres emboîtées suggère, au travers des foncés et des clairs, une suite \(1\), \(3\), \(5\), … : la suite des nombres impairs. L’organisation géométrique convainc de ce que la somme d’impairs consécutifs à partir de l’unité est un carré : \(1+3+5+7+9+11=6^2\) ; le carré du nombre d’équerres.

La propriété est donnée par Nicomaque de Gérase, originaire de Judée, qui a vécu vraisemblablement au II^e siècle de notre ère.

Un autre exemple : le triangle apparaît comme somme d’entiers.

Dans la figure 2, la somme \(1+2+3+4+5+6\) est représentée deux fois. Le calcul associé est un « pont aux ânes » de la classe de Première française, avec le fait d’associer deux triangles identiques pour former un nombre oblong, rectangle de longueur supérieure d’une unité à la largeur.

C’est efficace : pour le calcul des nombres triangulaires, on prendra la moitié du produit du côté (nombre de termes) et du successeur du côté, … \(n\) fois \((n+1)\) divisé par \(2\).

Ces nombres triangulaires ou triangles valent \(1\), \(3\), \(6\), \(10\), \(15\), …, \(\dfrac{n(n+1)}{2}\) pour le triangle de côté \(n\), de « racine » \(n\).⁴ Telle est la somme des \(n\) premiers entiers.

L’emploi des nombres figurés ainsi organisés en familles est une manière abstraite de penser les calculs sur les nombres entiers, avec une intention de généralité. Évidemment l’algèbre accomplit pleinement ce projet, et tout autrement. Ces nombres figurés ont cours jusqu’à la période moderne, sans cesse repris, étudiés, avec des publications encore aujourd’hui⁵. Ils s’inscrivent dans une longue tradition grecque, latine, hindoue et arabe. Par exemple, à ce sujet, un remaniement en latin de l’Introduction arithmétique de Nicomaque, par Anicius Boèce (fin V^e siècle, début VI^e siècle) a marqué le Moyen-Âge et est publié encore au XVI^e siècle (De institutione arithmetica libri duo, sur Gallica ).

Ce contexte géométrique n’est pas le seul à habiter les questions de nombres au cours des siècles. Une autre tradition arithmétique émane des Éléments d’Euclide (vers 300 ans avant J.-C.). Elle traite de questions de parité, de divisibilité, de nombres parfaits, amiables, de critères pour les nombres premiers, avec les manières de démontrer à ce propos dégagées des nombres figurés.

Outre cela, Diophante d’Alexandrie, ayant probablement vécu au II^e ou au III^e siècle de notre ère, est l’auteur d’une Arithmétique, incomplètement connue⁶. Cette œuvre est essentiellement une compilation de problèmes et de solutions : trouver un nombre (entier ou rationnel) satisfaisant à une certaine condition, à savoir résoudre une équation diophantienne⁷. Cette pratique arithmétique initie une nouvelle branche des mathématiques. Par les modes de traitement, le développement de quelques méthodes, l’apport de Diophante est fondateur. Il est considéré aussi comme initiant l’algèbre : il introduit des abréviations pour les inconnues, initiative promise à un bel avenir. En outre, Diophante a écrit Sur les nombres polygones, ouvrage dont on ne connaît qu’un fragment. Plusieurs traductions de Diophante marquent sa redécouverte à la Renaissance avec Bombelli, Xylander (ou Holzman), Stevin, etc. Gaspard Bachet de Méziriac s’inscrit dans cette lignée et publie en 1621 une édition gréco-latine de l’Arithmetica de Diophante. Elle contient les six livres sur l’arithmétique, le livre sur les nombres polygones, avec le texte grec et la traduction en latin. Bachet y adjoint deux livres appendices de sa main. En quelque sorte, cette publication de Bachet rassemble et transmet un héritage.

Ainsi que le dit Jean Itard : « Ce que nous avons à retenir ici c’est le rôle de tout premier plan que jouera Diophante pour l’Occident lorsqu’à la fin du XVI^e siècle, son œuvre sera connue, paraphrasée, éditée et traduite. Les mathématiciens qu’elle inspire sont légion : Bombelli, Albert Girard, Viète, Bachet de Méziriac, Fermat, Descartes lui-même, parmi bien d’autres. Nous sommes ici à l’origine de la théorie des nombres dans les temps modernes. »

Cet ouvrage est un terrain de recherche pour Fermat. Il annote abondamment l’édition qu’il possède. Ces annotations seront publiées après le décès de Fermat avec Les observations sur Diophante (1670). L’ouvrage annoté n’a pas été retrouvé. C’est là, notamment, que figure la célèbre observation, la deuxième, ouvrant sur la grande conjecture. Le problème est représentatif de ce qui deviendra la géométrie algébrique où Wiles va briller en la démontrant. C’est le grand théorème : il n’existe pas de nombres entiers strictement positifs \(x\), \(y\) et \(z\) tels que : \(x^n+y^n=z^n\) dès que \(n\) est un entier strictement supérieur à \(2\). Dans un commentaire de son Diophante, Fermat a affirmé en avoir une preuve que l’on n’a jamais retrouvée (exception faite du cas \(n=4\)) ; une preuve du théorème a été publiée par Andrew Wiles et Richard Taylor en 1995.

Le texte de Fermat, point de départ de cet article, est l’une de ces observations, mineure au regard de bien autres, l’observation 47 (l’avant-dernière) commentaire de la proposition 27 du Livre II de Bachet, appendice à son Diophante.

Contexte de la proposition de Bachet

En substance, la proposition 27 indique : « \(1=1^3\) ; \(3+5=2^3\) ; \(7+9+11=3^3\) ; \(13+15+17+19=4^3\), … » : les sommes des nombres impairs par groupes de \(1\), \(2\), \(3\), \(4\), \(5\) etc. sont respectivement égales au cube de l’effectif du groupe. Ce résultat est proche de celui concernant la somme des nombres impairs. Il a pu être connu des Anciens (Nicomaque de Gérase).

Sauf une exception, on ne trouve pas de figure dans l’appendice de Bachet. Celui-ci consiste en énoncés de propriétés accompagnés d’un texte d’explication et souvent d’un schéma. Le texte de la proposition 27 est ainsi fait, avec son schéma (figure 3) ; il est suivi d’une référence à l’ouvrage d’arithmétique de Francesco Maurolico publié en 1575, ouvrage faisant une large place aux nombres figurés de style analogue. Ce qu’écrit Bachet est proche de ce qu’a écrit Maurolico sur le même sujet : une mise en évidence des quatre premiers groupes et les sommes respectives donnant les cubes \(1\), \(8\), \(27\), \(64\). La somme totale des nombres impairs est un carré (voir figure 1) dont le côté est explicité : c’est le nombre (\(1\) ; \(3\) ; \(6\) ; \(10\) ; …) de termes sommés. Ce nombre est un triangle et il indexe les sommes (voir remarque 1  pour les détails de la justification).

Et en conclusion de cette explication d’exemple, Bachet écrit : « Ainsi cette proposition est claire » !

Le lecteur trouvera cependant une illustration possible (figure 4), très suggestive. On peut penser que, pour les praticiens anciens des nombres figurés, ceci n’est pas nécessaire comme s’il y avait appropriation mentale.

Le contexte des pages de l’écrit de Bachet (Appendice Livre II), sur lequel Fermat a réfléchi, est notamment fait de propositions comme :

• proposition 23 : la somme des nombres impairs égale à un carré ;

• proposition 24 : pour un certain nombre des premiers entiers, une expression du cube du plus grand terme à partir de la somme des précédents et du nombre de termes, soit le cube du plus grand égale la somme de son carré et de son produit par le double de la somme des précédents ; aujourd’hui on comprend : pour le \(n\)-ième entier, \(n^3=n^2+n\times2\dfrac{(n-1)n}{2}\) ;

• proposition 25 : la somme des cubes est le carré de la somme, carré dont le côté est le nombre de termes ; aujourd’hui on comprend : \(\displaystyle\sum_{{i=1}}^{n} i^3=\left(\sum_{{i=1}}^{n}i\right)^2=\left(\frac{n(n+1)}{2}\right)^2\) ;

• la proposition 26 signale que le carré ajouté au côté fait le double du triangle de même côté (aujourd’hui : \(n^2+n=n(n+1)\)), la 28 énonce que le cube, six fois le triangle de même côté et l’unité font une somme valant le cube suivant (aujourd’hui : \(n^3+6\dfrac{n(n+1)}{2}+1=(n+1)^3\)), comme un embryon du cube d’une somme…

Cette manière de faire, inductive, valait justification.

Observons aussi que l’expression en langage algébrique actuel ne doit pas faire perdre de vue qu’il s’agit à l’origine d’énoncés textuels assortis d’un exemple commenté. Du fait de la nature de l’algèbre, cette expression induit un biais. Elle porte à mettre en évidence une hétérogénéité de l’organisation des énoncés de Bachet. L’unité de cette organisation procède-t-elle de l’expression en terme de nombres figurés pour quelqu’un qui, comme Bachet, étudie Diophante et Maurolico ?

La proposition de Fermat, observation numéro 47

Étudions maintenant l’observation 47 de Fermat qui fait intervenir des nombres polygonaux.

Observation 47 de Fermat

Voici comment j’énoncerai cette proposition d’une façon plus générale : dans toute progression constitutive de polygone, l’unité constitue la première colonne ; la somme des deux nombres suivants, diminuée du premier triangle multiplié par l’excès sur \(4\) du nombre des angles du polygone, forme la seconde colonne ; la somme des trois nombres suivants, diminuée du second triangle multiplié par l’excès sur \(4\) du nombre des angles du polygone, forme la troisième colonne ; et ainsi de suite indéfiniment, suivant la même loi.

Fermat connaît le mode de génération des nombres polygones comme sommes de familles d’entiers. Cela peut résulter de toute son étude autour de ce même ouvrage de Bachet, de sa familiarité avec l’œuvre de Diophante ; les polygones sont aussi décrits comme sommes par Maurolico.

Fermat reprend l’héritage des nombres figurés, ce qu’il exprime par toute progression constitutive de polygone. En cela, il suit ce qu’a fait Diophante :

• les nombres triangulaires, sommes d’entiers ;

• les nombres carrés, sommes de nombres impairs ;

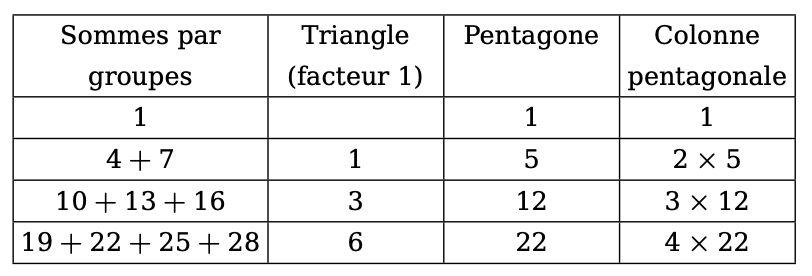
• les nombres pentagonaux, sommes successives des termes de la suite arithmétique de raison \(3\) et de premier terme \(1\), le nombre de termes sommés étant le côté du pentagone (figure 5) ;

• et ainsi de suite… avec une raison valant deux unités de moins que le nombre d’angles du polygone.

Manifestement Fermat maîtrise ce qui, à vrai dire, définit les nombres polygones. Puis Fermat avance une notion de colonne, ainsi qu’on en trouve dans l’ouvrage de Maurolico. Ce sont des empilements « spatiaux » de nombres figurés plans⁸.

Dans l’énoncé de la proposition 27 de Bachet, les sommes valent des cubes. En tant que nombres figurés, ce sont des configurations spatiales de « boules »⁹, empilements de carrés en nombre égal au côté ; des carrés présents parce que, dans ce cas, on ajoute des nombres impairs. Ces cubes sont des exemples de ce que Fermat nomme colonnes, les mêmes que celles de Maurolico.

Remarque 1 :  du point de vue du style mathématique, Fermat ne s’attarde pas sur le résultat de Bachet ; il n’en dit pas plus en termes de justification. Sur ce cas spécifique du carré, Fermat aurait-il pu procéder par comparaison de deux carrés et atteindre une démonstration du résultat de Bachet ? Pour préciser cela en termes actuels, avec la proposition 27 de Bachet, on considère les sommes de nombres impairs prises successivement en nombre de termes selon la progression arithmétique de raison \(1\) à partir de l’unité : \(1\), \(2\), \(3\), …, \(p-1\), \(p\). Avec quelqu’anachronisme, usant d’algèbre, la somme totale vaut le carré du nombre total de termes soit \(\dfrac{p(p+1)}{2}\) : \(\left(\dfrac{p(p+1)}{2}\right)^2\) ; et la somme totale, par sommes successives de \(1\), \(2\), \(3\), …, \(p-1\), des nombres impairs vaut \(\left(\dfrac{(p-1)p}{2}\right)^2\cdotp\) Avec la proposition 25 énoncée par Bachet : \(\left(\dfrac{p(p+1)}{2}\right)^2\) est somme des cubes, de là : \(\left(\dfrac{p(p+1)}{2}\right)^2-\left(\dfrac{(p-1)p}{2}\right)^2=p^3\). Ceci justifierait, au sens actuel, la propriété induite par la proposition 27.

Ou bien, un peu moins anachronique : soit \(T\) le triangle de côté \(p\), il égale la somme du triangle \(T’ ) de côté \(p-1\) et de \(p\) ; donc \(T^2=T’^2+2T’ \times p+p^2\) ; \(2T’ \) est rectangle oblong de côté \(p-1\) ; on trouve ainsi \(T^2=T’ ^2+p^3\).

Mais ceci ne figure pas dans les textes ! Bien que Bachet en ait été proche, la proposition 10 de l’Appendice I donne une (belle !) relation entre le polygone de côté \(n\) et celui de côté \(n+p\) (cf. annexe 1 1.1.1).

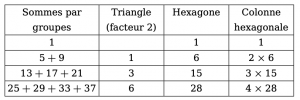
Remarque 2 : Fermat va plus loin, autrement, remarquablement. C’est l’intérêt de son énoncé. Et Fermat, ce faisant, s’est posé le problème des sommes analogues, non pas avec des impairs mais d’autres progressions numériques générant les pentagones, les hexagones, les heptagones, etc.

Ci-dessous, dans les premiers cas pour les pentagones et les hexagones, le triangle à soustraire est multiplié respectivement par \(1\), par \(2\) (pour le pentagone, l’excès sur \(4\) du nombre des angles vaut \(1\), le facteur multiplicatif est donc \(1\) ; pour l’hexagone, l’excès sur \(4\) du nombre des angles vaut \(2\), le facteur multiplicatif est donc \(2\)).

La figure 7 illustre les groupes d’effectif \(1\), \(2\), \(3\), etc. de termes de la progression de raison \(3\) et de premier terme \(1\), associée aux nombres pentagonaux.

La figure 8  illustre celle de raison \(4\) et de premier terme \(1\), associée aux nombres hexagonaux.

Sur un moment de calcul

Fermat exprime une propriété plus générale, ce qui est une ambition constante chez lui !

Ce résultat est exact¹⁰ dans ce degré de généralité, c’est donc un théorème de Fermat. Il est affirmé de manière inductive. Qu’on l’énonce dans le formalisme actuel, alors le sens « figuré » se perd… point de colonne, de triangles.

Souvent Fermat pratique ainsi, il énonce une propriété et n’en donne pas de démonstration ou la promet. Cela est encore plus le cas dans ses Observations, au format de commentaire, souvent brèves. En outre, ce style est pratiquement constitutif des nombres figurés, on l’a vu. C’est le cas avec l’écrit de Bachet, à ce qui se rapporte à la propriété 27, ainsi que celle de Maurolico. Depuis les Anciens, jusqu’au début du XVII^e siècle, cette forme, portée par la figure (devenue mentale), avec quelques premiers cas, apparaît probante : la somme des premiers impairs est le carré de leur nombre, la somme des premiers entiers est le triangle de côté leur nombre¹¹. C’est le propos même des nombres figurés de susciter cette conviction.

La forme et la présentation interrogent. Concernant ces sommes par groupes de \(1\), \(2\), \(3\), …, Fermat ne les exprime pas en tant que telles, il ne dit pas la somme vaut…. À ces sommes est soustrait un terme multiple d’un nombre triangulaire et le résultat vaut des colonnes, comme si était visé un nombre figuré.

Plus qu’un calcul, une propriété est mise en évidence.

Les énoncés en termes de nombres figurés sont généralement de type additif. Le recours, ici, à une différence a peut-être un accent moderne.

Par ailleurs, Fermat aurait-il eu en vue un énoncé plus général encore ? Des groupes définis autrement ? On peut voir en annexe 2 un exemple de proposition échappant au contexte des nombres figurés.

On ne sait pas quand a pu être écrit ce petit texte. Ce n’est pas un texte de premier plan et il ne semble pas avoir été repris comme c’est le cas pour ceux auxquels Fermat attachait de l’importance. Par exemple, pour rester dans le même contexte, l’énoncé du théorème des nombres polygonaux prolongeant des conjectures de Bachet : « Tout nombre est somme de \(1\), \(2\) ou \(3\) triangles ; de \(1\), \(2\), \(3\) ou \(4\) carrés, de \(1\), \(2\), \(3\), \(4\) ou \(5\) pentagones ; de \(1\), \(2\), \(3\), \(4\), \(5\) ou \(6\) hexagones ; de \(1\), \(2\), \(3\), \(4\), \(5\), \(6\) ou \(7\) heptagones ; et ainsi de suite indéfiniment. » C’est l’observation numéro 18, sur un commentaire de Bachet d’une proposition de Diophante. Elle figure aussi dans la lettre XII de Fermat à Mersenne (date indiquée septembre 1636) et, d’après Jean Itard¹², elle date plus vraisemblablement de 1638. Dans cette même lettre, faisant référence à la proposition 25 de Bachet, Fermat donne l’exemple \((1+2+3+4+5+6+7+8+9)^2=1^3+2^3+3^3+4^3+5^3+6^3+7^3+8^3+9^3\). Fermat a un peu plus de 30 ans et il est entré en relation (épistolaire) avec les savants de son époque depuis deux ans. Donné sans démonstration, l’énoncé du théorème des nombres polygonaux aura une belle postérité avec les preuves de Lagrange (1770) pour la décomposition en quatre carrés, de Gauss (1796) pour la décomposition en triangles, puis de Cauchy (1813) pour une preuve complète, etc.

Transition vers un autre monde des mathématiques

Cette propriété manifeste une solide expérience des nombres figurés, une dextérité calculatoire, un saut évident par rapport au travail de Bachet. Cependant on ne sait pas quelle forme de calcul Fermat a pu mettre en œuvre. On ne peut voir cet écrit seulement comme un résumé d’essais suffisamment convaincants. Aujourd’hui on pourrait faire un calcul algébrique de bon élève de Terminale, pas vraiment simple (voir l’annexe 1), mais un quelconque lien entre ce qu’énonce Fermat et ce type de calcul ne peut être avancé.

La formation de Fermat est imprécisément connue, elle émerge de ses travaux. Et, sans esprit réducteur, ne serait-ce que par les auteurs à partir desquels Bachet a travaillé, Fermat a eu accès à une vaste bibliothèque. Il connaît ses « classiques »¹³. Il est au fait de la science la plus récente. Fermat a en effet étudié Viète (1540-1603) — acteur majeur de la transformation de l’algèbre avec son livre phare, In artem analyticem isagoge, en 1591 — dont les œuvres sont republiées en 1624. Fermat l’évoque dans ses écrits et il l’utilise.

Le talent de « géomètre » de Fermat est évident ! Ici, en tant que calculateur inventif, « algébriste ». Il n’est que de consulter ses premières lettres pour le percevoir. C’est vrai au sens ancien à la manière de Diophante (traiter de questions de nombres dans un cadre peu symbolisé), c’est vrai aussi en un sens plus moderne, par algèbre ainsi qu’il le dit dans sa lettre à Roberval du 16 décembre 1636. Nombre de ses travaux en témoignent : l’étude des questions variationnelles, l’émergence de la notion de fonction, sa méthode de maximis et minimis, ses études de tangentes, ses avancées en théorie des nombres… En tout cela l’algèbre nouvelle devient un puissant moyen d’étude.

Pour « mineure » qu’elle soit, cette proposition n’est-elle pas à considérer comme un indice, au contenu établi, au procédé sybillin, d’une transition vers un autre monde des mathématiques ?

Références

1. Jean Aymès. « Beaucoup passeront et la science s’augmentera ». In : Bulletin de l’A.P.M.E.P. n° 519 (mai-juin 2016). .
2. Claude-Gaspard Bachet de Méziriac. Diophanti Alexandrini Arithmeticorum libri sex, et de numeris multangulis liber unus. . . .
3. Mireille Clapier et al. Pythagore, quelques aspects de l’arithmétique pythagoricienne. Toulouse : I.R.E.M., 1987.
4. Roshdi Rashed, Christian Houzel et Gilles Christol. Œuvres de Pierre Fermat, la théorie des nombres. Paris : Albert Blanchard, 1999.
5. Paul Tannery et Charles Henry. Œuvres de Fermat. Paris : Gauthier-Villars, 1894.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Jean Aymès est inspecteur pédagogique régional honoraire de mathématiques.

Annexes

Annexe 1 : à propos de la proposition 10 de Bachet Livre I

Elle revient, en termes modernes à ceci : pour un polygone de \(k\) angles, soit \(P_n^k\) le \(n\)-ième nombre polygone de \(k\) angles, où \(n\) désigne le côté (ou racine) ; on a : \(P_{n+p}^k\) = \(P_n^k+(k-2)np+P_p^k\).

Ce qui peut être vu comme une généralisation du carré d’une somme : au lieu de carré, on aura triangle, pentagone, hexagone, etc.

Pour une justification moderne, il suffit de partir de la définition par Diophante de \(P_n^k\) comme somme des \(n\) premiers termes de la suite de terme général \(\bigl[1+(i-1)(k-2)\bigr]\), \(i\) entier non nul. \[P_n^k=\sum_{{i=1}}^{n}\bigl[1+(i-1)(k-2)\bigr]=n+(k-2)\frac{(n-1)n}{2},\ \text{etc.}\] Avec cette égalité, la formule de Bachet est vérifiée sans problème.

Partie B : Proposition de calcul actuel à propos du commentaire 47

Pour un polygone de \(k\) angles, avec les mêmes sommes partielles (de Fermat, de Bachet) — que l’on note \(S_p^k\) pour une somme partielle de \(p\) éléments — et d’autre part un terme soustrait (ainsi que dit Fermat : produit du triangle précédent par l’excès sur \(4\) du nombre d’angles), le produit \((k-4)T_{p-1}\) ou \((k-4)P_{p-1}^3\) ou encore \((k-4)\dfrac{(p-1)p}{2}\cdotp\)

Et ce que Fermat désigne alors par colonne : \(S_p^k-(k-4)\dfrac{(p-1)p}{2}\cdotp\)

\(S_p^k=P_{\frac{p(p+1)}{2}}^k-P_{\frac{(p-1)p}{2}}^k\) ou, en nombres figurés, \(S_p^k=P_{T_{p}}^k-P_{T_{p-1}}^k\).

Or \(\dfrac{p(p+1)}{2}=\dfrac{(p-1)p}{2}+p\), selon la nature des nombres triangulaires d’être des sommes d’entiers.

D’où \(S_p^k=P_{\frac{p(p-1)}{2}+p}^k-P_{\frac{(p-1)p}{2}}^k\) ou \(S_p^k=P_{T_{p-1}+p}^k-P_{T_{p-1}}^k\).

La proposition de Bachet étudiée à la Partie A conduit à \(S_p^k=P_p^k+(k-2)\dfrac{(p-1)p}{2}p\) ou, en gommant l’aspect figuré : \(p+(k-2)\dfrac{p(p^2-1)}{2}\cdotp\)

La colonne \(C_{p}^{k}\) de rang \(p\) vaut ainsi \(C_{p}^{k}=p\left(p+(k-2)\dfrac{p(p-1)}{2}\right)\), c’est \(pP_{p}^{k}\). Ce résultat est figurable par un empilement de \(p\) nombres polygones \(P_{p}^{k}\).

Annexe 2 : expression des sommes de termes de la suite arithmétique de premier terme \({1}\), de raison donnée, par groupes de \({1}\), \({3}\), \({5}\), \({7}\), etc.

\(T_n\) désignant le \(n\)-ième triangle (aussi bien \(P_n^3\)) ; pour tout polygone ayant \(k\) angles et la progression qui le constitue : l’unité est la première somme ; la deuxième somme, constituée des trois termes suivants (de la progression) est égale à \(3[1+2(k-2)T_1]\) ; la troisième somme, constituée des cinq suivants, est égale à \(5[1+2(k-2)T_2]\) ; et ainsi de suite, la \(p\)-ième somme, constituée de \(2p-1\) termes, est égale à \((2p-1)[1+2(k-2)T_{p-1}]\).

Justification : ces termes de la suite générique de polygones ayant \(k\) angles sont ici distribués par groupes de \(1\), \(3\), \(5\), \(7\), … termes. Le \(p\)-ième groupe est constitué de \(2p-1\) termes, ceux pour \(i\) allant de \((p-1)^2+1\) à \(p^2\). La somme totale des termes (avec pour premier terme \(1\) et comme dernier terme \((p^2-1)(k-2)\)) vaut, par définition, le polygone \(P_{p^2}^{k}\). La somme cherchée pour le groupe est alors la différence \(P_{p^2}^{k}-P_{(p-1)^2}^{k}\). Le calcul conduit à \((2p-1)\bigl[1+2(k-2)T_{p-1}\bigr]\).

Le lien entre polygones et triangles exprimé par \(P_{p}^{k}=p+(k-2)T_{p-1}\) donne aussi pour cette somme \((2p-1)\bigl[1-2p+2P_{p}^{k}\bigr]\).

Cette proposition est un peu plus aisée à conjecturer que celle de Fermat et moins homogène dans l’expression en termes de nombres figurés. Il reste à méditer…

Maurolico a approché cela. Son livre, avec une étude conséquente de nombres figurés polyédriques se termine par la mise en évidence de la somme des nombres impairs par groupes de \(1\), \(3\), \(5\), \(7\), etc. Elle vaut ce qu’il nomme (nombre) octaèdre (aujourd’hui dodécaèdre rhombique) ; somme dont il énonce qu’elle égale la différence de deux bi-carrés successifs. Ce qu’aujourd’hui on énonce : par groupes successifs d’effectifs impairs, la \(p\)-ième somme des nombres impairs vaut \(p^4-(p-1)^4\). Et Maurolico de conclure : ceci n’est pas peu admirable.

En outre, dans sa lettre XII, Fermat traite d’une autre généralisation. La somme des cubes des entiers à partir de \(1\) lui inspire la question : étant donnés autant de nombres en progression arithmétique que l’on voudra, et connaissant la raison de la progression et le nombre de termes, trouver la somme de leurs cubes. Fermat développe sa réponse. Pour ce faire, il a recours à la somme des carrés qu’Archimède a traitée dans Des spirales ; puis il donne une méthode pour le calcul des sommes des puissances quatre et annonce avoir résolu le problème pour la somme des puissances quelconques…

---

1. Il s’agit de l’observation 47.↩︎

2. Selon la traduction du latin telle que donnée par Paul Tannery et Charles Henry, Œuvres de Fermat.↩︎

3. Cependant la forme n’est pas figée, un losange pourrait convenir, éventuellement éclairer une propriété.↩︎

4. Pour le rang \(n\), le nombre triangulaire vaut \(\dfrac{n(n+1)}{2}\) et le nombre carré \(n^2\) ; inversement, le nombre figuré étant donné, trouver l’entier \(n\), c’est trouver sa racine. Ainsi \(4\) est racine du nombre triangulaire \(10\). Ce mot demeure dans l’expression racine carrée.↩︎

5. Ainsi l’ouvrage Figurate numbers, Elena Deza, Michel Marie Deza, World Scientific, 2012.↩︎

6. Sur treize livres, six étaient conservés, quatre autres ont été retrouvés en 1971.↩︎

7. Dans le vocable adopté actuellement, il s’agit d’une équation polynomiale à coefficients et inconnues entièrs ou rationnels.↩︎

8. Voir l’article Jeux de boules, Henry Plane, Au fil des maths n° 534, .↩︎

9. Visualisation commode, cependant la « plasticité » nécessaire des figures relatives aux formes des nombres figurés impose des boules de rayon nul !↩︎

10. La traduction que fait Émile Brassine dans son Précis des Œuvres de Fermat (1853) le conduit à douter du calcul, il traduit une addition à la place d’une soustraction ; ce doute n’est guère fondé, la traduction de Paul Tannery et Charles Henry doit être suivie. Merci à Joëlle San Juan-Pasty, latiniste, pour son aide à clarifier cela.↩︎

11. Pour une réflexion sur diverses démonstrations, voir par exemple l’article Variations autour d’une formule, Attila Mádec et Zoltán Matos, Au fil des maths n° 533, .↩︎

12. Article Sur la date à attribuer à une lettre de Fermat, Revue d’histoire des sciences, 1948.↩︎

13. Dans sa lettre à Mersenne du 26 avril 1636, la première connue, il évoque Apollonius et Viète.↩︎

---