Et si on modélisait ?

Cet article pose les enjeux de l’activité de modélisation en mathématiques : les enjeux pour les élèves lorsqu’ils sont confrontés à un problème de modélisation, mais aussi les enjeux pour l’enseignant qui doit faire travailler cette compétence dans ses classes. De quoi approfondir le concept pour ensuite se lancer avec ses élèves !

Gaëlle Bugnet et Vicky Kass-Canonge

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Introduction

Dans le cadre d’un master professionnel de formation de formateurs, nous avons réalisé une activité de modélisation pendant trois mois en collaboration avec Nadia Herizi et Ludovic Hamard, sous la direction d’Alain Kuzniak. Ce fut une excellente occasion de nous documenter sur le concept de modélisation en mathématiques et de porter un regard critique sur les exercices estampillés « modéliser » disponibles dans nos manuels de cycle 4. Et bien sûr, nous nous sommes confrontées nous-mêmes aux difficultés de la tâche : les mêmes que celles que rencontrent nos élèves, à savoir construire un modèle mathématique cohérent et le faire évoluer pour qu’il permette de répondre à notre problème, et la difficulté supplémentaire spécifique aux enseignants, c’est-à-dire trouver une bonne situation à modéliser. Tout cela n’est guère aisé, nous le verrons.

Qu’entend-on par « modéliser » ?

Le cycle de modélisation

D’après le dictionnaire Le petit Robert, modéliser c’est « établir le modèle de quelque chose », et un modèle est la « représentation simplifiée d’un processus, d’un système ». En mathématiques, modéliser c’est établir une représentation simplifiée d’une situation réelle afin de l’expliquer, au moins partiellement, ou encore en prédire l’évolution, par des théories mathématiques.

Pour notre travail de master, nous nous sommes basés sur un cycle de Blum et Leiss (2007), qui propose une modélisation en sept étapes.

On part d’une situation réelle qu’on simplifie (situation modèle). On prend en considération un certain nombre de paramètres réels (modèle réel), et on applique un modèle mathématique avec ces paramètres, pour effectuer une simulation. On confronte les résultats de la simulation aux résultats réels, ce qui permet de valider, affiner ou invalider le modèle envisagé.

Lorsque la comparaison des résultats obtenus aux résultats réels met en défaut un modèle proposé, on peut être amené à modifier des paramètres voire choisir un autre modèle, et ainsi parcourir le cycle à plusieurs reprises.

La modélisation au cycle 4

Les textes officiels

Le document ressource du cycle 4 «Modéliser» [1] reprend l’idée du cycle de Blum et Leiss : « On peut en effet décrire de manière schématique le processus de modélisation en distinguant trois temps : la mise au point d’un modèle à partir du réel, le fonctionnement du modèle lui-même à l’intérieur des mathématiques, et la confrontation des résultats du modèle au réel » en précisant que «dans une version plus élaborée, cette dernière phase boucle sur la première, en construisant une version améliorée du modèle.»

Comme nous allons le voir dans la description de notre travail de modélisation, exploiter «le réel» peut s’avérer très complexe ; le document ressource met d’ailleurs en garde : « [la] compétence “ Modéliser ” est, parmi les compétences travaillées, celle qui aborde de front le lien des mathématiques avec un extérieur à la discipline. Définir précisément cet extérieur n’est pas chose aisée, car il n’est pas certain qu’on puisse simplement l’envisager ou le nommer sans disposer déjà d’un minimum de concepts, de théories, de modèles déjà plus ou moins liés aux mathématiques. Ceci étant, quel que soit le terme utilisé […], la modélisation fait intervenir un élément non mathématique au début et à la fin du processus. »

Le programme officiel du cycle 4 décline la compétence « modéliser » comme suit :

reconnaître un modèle mathématique (proportionnalité, équiprobabilité) et raisonner dans le cadre de ce modèle pour résoudre un problème ;
traduire en langage mathématique une situation réelle (par exemple à l’aide d’équations, de fonctions, de configurations géométriques, d’outils statistiques) ;
comprendre et utiliser une simulation numérique ou géométrique ;
valider ou invalider un modèle, comparer une situation à un modèle connu (par exemple un modèle aléatoire).

La réalisation des quatre items correspond au cycle complet. En effet alors que le premier point aborde le modèle mathématique et le passage de celui-ci aux résultats mathématiques, le deuxième correspond au passage d’une situation modèle au modèle réel. L’interprétation des résultats mathématiques se retrouve dans « Comprendre et utiliser une simulation numérique ou géométrique » et finalement on retrouve la comparaison des résultats mathématiques aux données de la situation modèle afin de valider ou d’invalider le modèle.

Cependant, la lecture du programme nous laisse penser que pour travailler la compétence modéliser, il suffit d’aborder au moins un des items décrits.

Réaliser de vraies tâches de modélisation avec les élèves, en parcourant le cycle complet une voire plusieurs fois, peut ainsi paraître extrêmement ambitieux. C’est pourtant ce que nous préconisons de faire, suite à notre propre travail, et nous espérons vous donner, dans la suite de cet article, des clés pour vous lancer sans appréhension. Mais auparavant, un petit détour par nos manuels…

Dans les manuels

Voici quelques exemples d’exercices estampillés « modéliser », qu’on trouve dans différents ouvrages scolaires de cycle 4.

Transmaths cycle 4 exercice 83 page 178 [2]

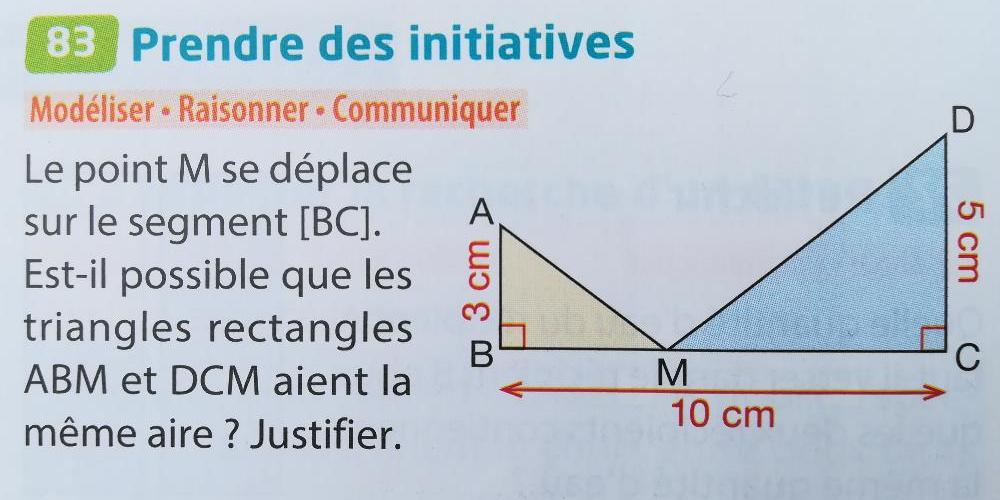
Cet exercice se trouve dans le chapitre « Modéliser une situation ». En consultant la page « J’apprends le cours » de ce chapitre, on y lit uniquement des techniques de résolution d’équations. L’exercice proposé s’intègre bien dans une partie « mise en équation », mais peut-on considérer qu’il s’agit d’une activité de modélisation ? Le problème est géométrique, on ne part pas d’un « extérieur » au domaine mathématique. Aucun choix n’est à faire, seul un changement de cadre est nécessaire à la résolution de l’exercice. Cet exercice relève plutôt de la compétence « représenter ».
Maths monde cycle 4 page 259 [3]

Cet exercice de découverte demande aux élèves de traduire une situation concrète en termes mathématiques, puis de proposer une, ou plutôt, la solution. Une confrontation à des données réelles peut éventuellement être envisagée en effectuant une vérification à l’aide de tailles d’élèves.
Transmaths cycle 4 page 319 [2]

La situation travaillée propose des données réelles mais très simplifiées. Le modèle est imposé par l’énoncé et l’item «traduire en langage mathématique une situation réelle» est travaillé, mais de manière très guidée. En revanche, nous ne retrouvons pas les autres étapes du cycle. Les exercices 2. et 3. sont très similaires d’un point de vue « modélisation ». Pour le dernier, il serait tout de même envisageable de remettre en question les données et donc le modèle.
Transmaths cycle 4 page 295 [2]

La figure de cet exercice n’est pas codée. C’est l’observation du réel qui permet de faire par exemple l’hypothèse que les murs sont verticaux, que le toit est symétrique (cette seconde hypothèse étant par ailleurs inutile). On demande aux élèves de faire des hypothèses sur les surfaces et de reconnaître un modèle géométrique. Par la suite, ils raisonnent dans le cadre de ce modèle afin d’apporter une réponse au problème. Il convient d’être vigilant et d’expliciter que les choix de surfaces sont un choix de modèle et non un « implicite » de l’énoncé.

Maths Myriade Cahier de compétences 3 Myriade page 97 [4]

Cette tâche part d’une situation réelle. Le modèle qui consiste à considérer que le téléphérique avance à vitesse constante, est imposé. Cependant, le choix d’une configuration de Thalès, avec ou sans triangle rectangle, est laissé aux élèves. De plus, la tâche peut être traitée dans plusieurs cadres. Il est envisageable de raisonner à l’aide de triangles semblables, de penser à une situation de proportionnalité ou encore de proposer une solution à l’aide de la trigonométrie. La traduction en langage mathématique, constitue donc un réel enjeu ici. Après avoir trouvé une solution, on peut la confronter à des données réelles ; l’enseignant peut en effet projeter les caractéristiques techniques des œufs de la Bastille qui se trouvent ci-dessous :

Source : Wikipedia
Données techniques Dénivelé entre les quais d’embarquement : 266 m (altitudes de 216 à 482 mètres); Longueur sur la pente : \(700\) m; Vitesse : \(0\) à \(6\,m · s^{−1}\); Vitesse du vent déclenchant une mise en sécurité : \(54\, km · h^{−1}\); Temps de parcours : variable, entre \(3\) et \(4\) minutes.

Sans recommencer le cycle de modélisation, une discussion sur la vitesse, constante ou moyenne, peut s’enclencher et certains élèves peuvent nuancer le résultat qu’ils ont obtenu.

Les deux dernières situations se rapprochent le plus d’une tâche de modélisation telle qu’on l’a définie en préambule. En revanche, dans tous les exercices, on manque de données réelles pour être à même de valider ou d’invalider le modèle.

Il nous semble primordial que les élèves appréhendent la notion de cycle de modélisation. Or dans les exercices que nous avons vus dans les manuels, il s’agit toujours d’une exploitation partielle de celui-ci. S’il peut être intéressant de traiter ce type de tâche afin de travailler plus particulièrement une ou plusieurs étapes du cycle de modélisation, la répétition de ces exercices nous semble insuffisante pour former les élèves à la notion de modélisation.

Description de notre travail de modélisation

Avant de nous lancer avec les élèves, c’est à nous de nous confronter à une tâche de modélisation. La critique des manuels de cycle 4 est aisée, mais nous allons voir que la réalisation d’un travail de modélisation ambitieux est semée d’embûches.

Genèse et ambition première

La recherche d’une situation à modéliser qui convienne nous a posé quelques difficultés, étant donné que nous partions de rien : pas de thème ni de contexte ni de niveau imposé. Nous avons passé plusieurs heures à chercher un thème. Étant limités en temps, il allait être difficile de rencontrer de bons interlocuteurs, trouver de bonnes données, comprendre certains modèles mathématiques…Plusieurs idées nous intéressaient, mais nous ne voyions pas où elles pouvaient nous mener mathématiquement…Jusqu’à ce qu’on lise dans Le Canard Enchaîné du 15 mars 2017 l’article suivant :

Ayant déjà entendu parler d’outils mathématiques pour étudier les files d’attente, nous avons décidé de nous pencher sur le problème de la saturation du Louvre le jour de l’ouverture de l’exposition Vermeer.

À la recherche d’informations plus précises que celles données dans ce petit article, nous nous sommes vite rendu compte que les données chiffrées des articles de journaux étaient imprécises, voire contradictoires. Ainsi le premier jour de l’exposition a eu lieu le 22 février et non le 21 comme mentionné dans l’article ci-dessus. De plus, le journaliste a confondu la salle d’exposition temporaire qui peut accueillir 450 visiteurs avec le hall Napoléon qui, lui, a une capacité d’environ \(2500\) personnes.

Nous avons donc tenté par voie officielle d’obtenir des données auprès du musée, mais ces informations nous ont été refusées. Il a été plus efficace de se rendre sur place et d’obtenir des renseignements en comptant, observant, et discutant avec des agents d’accueil ou de sécurité.

Nous avions tout d’abord envisagé des problématiques ambitieuses visant à proposer des solutions contre l’engorgement, mais nous avons dû restreindre notre travail à la description et à l’explication du phénomène plutôt qu’à la prévention. En effet, avec pour seules données celles trouvées dans la presse et celles glanées sur place auprès du personnel, la simulation de l’engorgement lors de l’exposition s’avérait être une tâche suffisamment ample et complexe. Voici la problématique que nous avons traitée :

Premier jour de l’exposition Vermeer au Louvre le 22 février 2017 : des visiteurs n’ont pas pu y accéder. Pourquoi ?

Réalisation effective du projet

Nous étions quatre à travailler sur cette question ; nous avons commencé par travailler de façon indépendante sur différents modèles mathématiques envisageables. En parallèle, nous avons réfléchi à des activités pour la classe en relation avec ce sujet, que nous évoquerons plus loin.

Tout d’abord, la notion de modélisation des files d’attente évoque la loi de Poisson, mais il a fallu se rendre à l’évidence que vu l’engorgement de nos files d’attentes, le modèle de la loi de Poisson n’était pas applicable.

Ensuite, trois modèles plus ou moins simples ont été envisagés, et des simulations ont été effectuées à l’aide de feuilles de calcul, de GeoGebra et de programmes Python. Les simulations à l’aide du tableur et de GeoGebra ont envisagé l’hypothèse d’un rythme des arrivées régulier dans la file d’attente et un temps de visite constant ; la simulation à l’aide du logiciel Python a permis d’aborder un modèle plus évolué avec des durées de visite suivant une loi normale.

Nous sommes parvenus à l’aide de ces simulations à illustrer la saturation rapide du hall Napoléon, et à reconstituer des scénarii possibles correspondant aux quelques données trouvées dans la presse.

Il s’est avéré que deux modèles différents ont fourni des résultats correspondant aux faits réels. Le temps de visite des spectateurs n’est certainement pas constant, donc l’un de ces deux modèles est d’évidence une simplification grossière de la réalité. Il a été ainsi mis en évidence que le fait de trouver un modèle dont les résultats correspondent à la réalité ne signifie pas que ce modèle est valable. Cet aspect est important et nous a donné à réfléchir… Particulièrement sur le fait que c’est un point que nous n’avions jamais abordé en classe.

Chaque étape de notre projet nous a permis de récolter des données réelles aboutissant à des tâches pour la classe, mettant plus ou moins en œuvre la compétence mathématique «modéliser». Nous proposons des activités géométriques pour la classe de Seconde (Annexe 1), un travail autour de la proportionnalité utilisant une feuille de calcul pour le cycle 4 (Annexe 2), un travail en analyse sur les fonctions affines (2). Enfin nous avons créé une activité inspirée des projets de type «LEMA» [5], « Le problème de l’escalier mécanique », qui a été testée lors de deux ateliers aux Journées de l’APMEP (à Nantes et Bordeaux) et en formation. C’est cette expérience que nous allons décrire dans ce qui suit.

Une expérience de modélisation sur le temps court

Une source d’inspiration : le projet LEMA

On a vu en première partie qu’une modélisation peut être représentée par un cycle dont on fait un certain nombre de fois le tour, et qu’il est évidemment difficile de concevoir une activité en classe qui se déroule sur un temps maximal de cinquante-cinq minutes dans l’idée de parcourir le cycle dans son intégralité.

Dans le cas d’activités de modélisation adaptées, la confrontation de différents modèles choisis au sein de la classe, lors de la synthèse de l’activité, peut permettre à l’enseignant de faire réfléchir les élèves sur la pertinence de chacun, de montrer l’importance du choix du modèle, et la nécessité parfois de le faire évoluer.

Le projet européen LEMA (Learning and Education in and through Modelling and Applications et enseignement dans et par la modélisation et les applications) propose des situations permettant de travailler cette compétence dans des conditions correspondant aux conditions réelles d’enseignement. En voici un exemple.

L’idée est de partir de situations concrètes simples. L’énoncé est facile d’accès, les élèves peuvent se l’approprier rapidement, et entrer dans l’activité mathématique de modélisation.

Le problème de l’escalier mécanique

Inspirés par ces « tâches LEMA », nous avons créé une tâche de ce type à partir d’une photographie prise dans le hall du musée du Louvre.

Voici l’exercice proposé :

Au bout de combien de temps la 400^e personne de la file d’attente sur le parvis du Carrousel du Louvre arrive-t-elle en bas de l’escalier mécanique ?

Cet exercice peut s’inscrire dans le programme de cycle 4 : il s’agit de reconnaître une situation de proportionnalité, l’idée étant de déterminer le débit des arrivées en bas de l’escalier mécanique. Les élèves travaillent aussi les ordres de grandeur dans cet exercice.

Étudions comment un tel exercice fait travailler la compétence de modélisation :

« Reconnaître un modèle mathématique » : l’élève doit reconnaître le lien entre la vitesse de l’escalator et la durée d’attente. Le professeur aura à sa disposition la vitesse standard d’un escalator, ou lui permettra d’aller faire une recherche à ce sujet. On peut aussi imaginer une simulation « réelle » de l’avancée d’un escalator par les élèves pour calculer la vitesse.
« Traduire en langage mathématique une situation réelle» : cette traduction est inévitable pour proposer une solution. On peut travailler uniquement algébriquement sur des vitesses, on peut faire un schéma, certains calculent les angles… Les modèles proposés peuvent ne pas être efficients.
Avec cette tâche, « comprendre ou utiliser une simulation »ne peut pas être travaillé dans le temps court. Il s’agirait dans un deuxième temps (un prolongement de l’activité à la maison, ou lors d’une séance informatique…) de proposer une simulation avec les résultats obtenus.
« Comparer une situation à un modèle connu » est assez délicat. Les élèves pourraient par exemple être tentés de tracer des triangles rectangles, ce qui n’est pas nécessaire et complique la tâche. En revanche, réfléchir à l’ordre de grandeur des solutions peut permettre de « Valider ou invalider un modèle ». Des modèles peuvent aussi s’« auto-invalider » car ils ne permettent pas de résoudre le problème. On peut également imaginer (hors la classe) une expérimentation concrète avec chronométrage. Dans tous les cas, on ne pourra pas, lors d’une première approche de l’exercice, confronter les résultats aux résultats réels qu’on ne connaît pas.

Ainsi, cette tâche permet essentiellement de travailler la traduction d’un problème concret en langage mathématique et la reconnaissance d’un modèle de proportionnalité. Elle permet aussi de travailler la validation d’un modèle par une approche en termes d’ordre de grandeur.

Différence avec les exercices des manuels

Comparons cette tâche aux exercices proposés dans les manuels présentés en première partie. L’exercice n’est pas du tout guidé, de sorte que la modélisation est intégralement dévolue à l’élève. Ainsi, la vitesse d’un escalator, même si elle est nécessaire à l’estimation, n’est pas donnée d’emblée. Il est conseillé d’attendre que la nécessité se fasse sentir. Et une fois la question posée par l’élève ou le groupe d’élèves qui en ressent le besoin, on pourra au choix donner la vitesse habituelle d’un escalier mécanique, soit environ \(2 \ km \cdot h^{-1} \), ou \( 0,6 \ m \cdot s^{-1}\), ou une fourchette de valeurs (entre \(1,8\) et \(2,8 \ km \cdot h^{-1}\))… On a ici un levier de différenciation. On peut aussi demander à l’élève d’effectuer une recherche à ce sujet.

Avec cette imprécision des données (figure, vitesse), il faut se rendre à l’évidence qu’il n’y a pas « une » solution à l’exercice, ce qui peut paraître inconfortable, que ce soit pour l’élève ou l’enseignant. Inconfortable mais formateur, car nous nous attaquons là à une conception très ancrée chez nos élèves. Alors qu’il nous paraît indispensable de la « casser » régulièrement, il arrive au contraire que nous contribuions involontairement à maintenir cette conception erronée, en variant peu les types d’exercices proposés en classe.

Réactions des participants à l’atelier.

Cet exercice a fait sortir les collègues qui l’ont testé de leur zone de confort : certains ont été déstabilisés par le fait que la réponse ne soit pas connue. Plusieurs collègues nous ont demandé, à l’issue de l’atelier « Alors, c’était quoi la réponse ? ». Il paraît par conséquent indispensable de proposer une formation continue sur la modélisation : inclure des situations de modélisation dans ses cours semble en effet toucher à la conception-même des mathématiques que nous pouvons avoir, et nécessite de changer ses habitudes d’enseignement, ce qui n’est guère aisé sans accompagnement.

Une autre question s’est posée : comment évaluer cette activité ? Une évaluation « naturelle » serait par compétences : on peut détailler les items de la compétence « modéliser », évaluer la compétence « calculer », et éventuellement la compétence « communiquer » si on demande par exemple une narration de recherche dans un travail de groupe.

Points communs entre les deux types d’activité

On peut trouver un certain nombre de points communs entre le travail de modélisation réalisé en master (sur le temps long) et le travail sur l’escalator réalisé lors de l’atelier (en 45 minutes). Tout d’abord, que ce soit lors de notre travail de master ou lors de l’atelier des journées, il y a eu une période de flottement à l’entrée dans l’activité. On ne voit pas d’emblée par quel bout prendre le problème.

Dans un deuxième temps, on s’approprie l’objet d’étude et une modélisation prend forme. À partir de ce modèle, on a des appuis concrets pour travailler.

La phase suivante est celle de la réalisation, ou du calcul : c’est cette phase qu’on pourrait qualifier de réjouissante.

Enfin, on obtient un résultat, qu’on peut valider ou pas, ou plusieurs résultats qu’on peut confronter aux autres ou à la réalité.

Conclusion

Notre travail sur le temps long nous a permis d’apprécier les difficultés pour définir les contours d’une modélisation. Obtenir des données fiables, puis créer un modèle adéquat n’est pas aisé lorsqu’on part d’une situation réelle, nécessairement complexe. Il apparaît donc peu surprenant que les exercices des manuels ne reflètent pas entièrement la réalité. Néanmoins il nous paraît souhaitable que les tâches estampillées « modélisation » proposent de travailler au moins une partie du cycle défini en introduction et ne constituent pas uniquement un enrobage concret à solution unique d’un problème mathématique.

L’activité menée lors de notre atelier « Modélisation : le Louvre victime de son succès » a permis de mettre en évidence que la mise en situation de l’enseignant dans une activité de modélisation peut lui permettre de mieux appréhender les obstacles cognitifs et mathématiques auxquels les élèves pourront être confrontés en classe. De plus, la connaissance du cycle de modélisation permet de mieux comprendre les enjeux de la modélisation et donc les limites de nombreux exercices de manuels. L’enseignant peut ainsi compléter ou modifier certains exercices, déjà bien aboutis comme on l’a vu lors de la description de la tâche concernant les œufs de Grenoble ou même celle du mousseur de douche.

Les activités de modélisation peuvent paraître longues et fastidieuses mais, comme le montrent les problèmes créés par le projet LEMA par exemple, loin d’être irréalisables. Elles peuvent procurer une réelle satisfaction aux élèves qui auront produit un résultat en ayant été acteurs de tout le processus. Pour changer le regard de l’enseignant sur la modélisation, il serait souhaitable qu’il l’expérimente lui-même, en formation par exemple. Nous vous engageons à tenter l’expérience : vous serez surpris !

Références

Éduscol. Document ressource cycle 4. Modéliser. . Mars 2016.↩
Transmaths cycle 4. Hachette, 2016.↩
Maths monde cycle 4. Didier, 2016.↩
Maths Myriade. Cahier de compétences 3 e. Bordas, 2018.↩
LEMA. Learning and Education in and through Modelling and Application. .↩
Manuel Pean et Laurent Hivon. Modéliser avec le numérique. . Académie d’Orléans-Tours.