Pas de probas, pas de chocolat !

Expériences aléatoires, lois discrètes et continues, approximation des unes par les autres, intervalles de confiance, fluctuations d’échantillonnage, tests statistiques, paradoxes probabilistes. . . Un menu riche et croquant, qui passe quand même mieux avec des friandises.

Karim Zayana

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

De la tartine de chocolat au paradoxe du chat beurré

Forrest aime le chocolat¹ [9]. Philosophe et probabiliste à ses heures, il s’est rendu célèbre grâce à cette phrase culte, tube planétaire à la réflexion pénétrante : « La vie c’est comme une boîte de chocolats, on ne sait jamais sur quoi on va tomber ». Tirer au sort des chocolats est certes une activité intéressante. Mais aujourd’hui, Forrest s’occupe avec un petit pain suédois. Consciencieusement, il le nappe de sa pâte chocolatée préférée. Souriant devant la caméra, il place habilement quelques références produit (le dentifrice xxxx à la menthe ; le xxxx aux noisettes), quand soudain, c’est le drame. En plein direct. Un faux mouvement sur un geste pourtant répété cent fois dans la loge avec son téléphone portable. La tartine tombe. L’image défile sur les télévisions, semant l’effroi chez les millions de foyers rivés à ce programme familial. En léger déséquilibre, le goûter de Forrest se retourne. Une seule fois – le ralenti est formel. En effet, le chocolat, trop lourd (Forrest n’a pas lésiné), empêche la rotation de se poursuivre : pas assez d’élan. Et cette chute, inexorable. Une mère voudrait masquer les yeux de sa fille. Un père couvrir ceux de son fils. Aimantés par l’écran, ils suivent pourtant la scène, médusés, tandis que Bill jappe, flaire et salive de désespoir devant les insoutenables gros plans. Puis le choc : face contre terre.

Fracas. Silence. Coupons ! Reprenons l’expérience. Soit la probabilité $p$ que « la tartine tombe côté chocolat », et $q=1-p$ celle de l’événement contraire : « la tartine tombe côté croûte ». Dans les deux cas, la tartine sera moins bonne à manger. Et endommagée, ce qui compromet l’indépendance théorique de deux expériences successives et pourrait influer sur le paramètre $p$, au début très proche de 1, puis de moins en moins à mesure que la pâte se détache. Mais faisons comme si de rien n’était. Chaque chute est une réalisation de Bernoulli $\mathscr{B}(p)$. Deux questions classiques émergent [3] :

après $n$ tels crash tests, à quelle loi obéit le nombre $S_n$ de chutes côté croûte ? Une loi binomiale de paramètres $n$ et $p$, dès lors :
$$\mathbb{P}(S_n=k) = \begin{pmatrix}n\\k\end{pmatrix} p^{n-k}q^k\ ;$$

quelle loi gouverne le rang $T$ de la première chute côté croûte?Une loi géométrique de paramètre $q$, ainsi :</
$$\mathbb{P}(T=k)=p^{k-1}q.$$

La première question s’accompagne souvent d’un calcul classique d’espérance : $E(S_n)=np$. Fait notable, une fois traitée, la deuxième question fournit une démonstration probabiliste de la somme d’une progression géométrique. Pour cela, on considère la probabilité que la tartine tombe côté croûte au moins une fois à l’issue de $n+1$ jets. Cette dernière vaut $1-p^{n+1}$ en examinant l’événement contraire. Mais elle vaut aussi $q+pq+\dots+p^nq$ en partitionnant l’étude grâce au système d’événements $T=1, T=2, \dots T=n+1$. On a donc $q(1+p+\dots+p^n)=1-p^{n+1}$, d’où l’on tire, après division par $q=1-p$, la formule connue.

Ne terminons pas sans avoir évoqué le temps moyen d’attente $E(T)$ avant d’obtenir une chute côté croûte. Il suffit de sommer :
$$E(T) = \sum_{k \geqslant 1} k\mathbb{P}(T=k) = q \sum_{k \geqslant 1} kp^{k-1}$$
qui vaut² $ \dfrac{q}{(1-p)^2} = \dfrac{1}{q}\cdotp$

Refermons cette partie sur le paradoxe du « chat beurré ». C’est bien connu, Schrödi retombe toujours sur ses pattes. Forrest, décidément maladroit, renverse un pot de beurre de cacao sur le dos du chat. Il attrape l’animal pour le nettoyer. Mais Schrödi, toutes griffes dehors, miaule, s’agite, s’échappe, et saute dans le vide. Le chocolat l’attire d’un côté, ses pattes de l’autre. Tournoyant tel un cosmonaute, défiant les lois de la Physique classique, Schrödi restera suspendu en lévitation un mètre au-dessus du sol…

Œufs surprises, la loi du collectionneur

Charlie aussi aime le chocolat [1]. Petit garçon, on raconte qu’il a trouvé un coupon gagnant dans un délice à la guimauve. Depuis, il a grandi, fondé sa chocolaterie, mais gardé son âme d’enfant. Chaque soir, il prélève un œuf surprise en sortie de son usine et construit le petit jouet. On suppose que la collection comporte $r=100$ modèles différents de jouets, tous distribués dans une même proportion et aléatoirement. Quel temps U (en jours) Charlie patientera-t-il afin de réunir les r pièces différentes ? En voilà une question !

On modélise le problème de la façon suivante: on considère que Charlie a déjà recueilli $k-1$ jouets distincts ($k \leqslant r$). Appelons $T_k$ le délai nécessaire pour découvrir une nouvelle pièce (différente des $k-1$ déjà trouvées). Bien entendu, $T_1=1$ et $U=T_1+T_2+\dots+T_r$. Comme vu dans la partie précédente, la variable aléatoire $T_k$ suit une loi géométrique de paramètre $p_k =
\dfrac{r-k+1}{r}\cdotp$ Donc $E(T_k) = \dfrac{r}{r-k+1}\cdotp$

$$\text{Puis }E(U) = \sum_{k=1}^{r} \frac{r}{r-k+1} = r \sum_{k’=1}^{r}
\frac{1}{k’} \approx r \ln(r).$$
Il faudra en moyenne un peu plus d’un an à Charlie pour réunir tous les jouets…

Fondue au chocolat, quand le discret devient continu

Cette partie est à la croisée des deux autres. Elle articule la loi binomiale à la loi gaussienne, s’applique aux statistiques inférentielles et reprend les approches déjà très fécondes proposées dans [4] et [8].

Une grande somme de variables aléatoires identiquement distribuées et indépendantes « se comporte » comme une gaussienne, voilà la tendance qu’exprime le théorème central limite. L’énoncé, dans le cas particulier d’une addition $S_n$ de variables de Bernoulli (Suisse, XVII^e) de paramètre $p$, est connu sous les noms de Moivre-Laplace (tous deux Français, XVIII^e).

Visuel, le phénomène est frappant quand $p = \dfrac{1}{2}$ sur une planche de Galton³ (Anglais, XIX^e), figure 1 à main levée. Une pièce en chocolat lâchée du haut du support incliné, roule dans le graphe comme à travers un réseau capillaire. À chaque étage, elle hésite entre sa gauche, codée par le chiffre $0$ et sa droite, codée par le chiffre $1$. Cette marche aléatoire reproduite de nombreuses fois montre une répartition en cloche d’un trésor qui s’entasse. La même expérience, en faisant cette fois couler une quantité identique de chocolat fondu à l’intérieur de la galerie engendrerait une surface lisse et bosselée, de même aire totale⁴ puisqu’il y a la même quantité de chocolat.

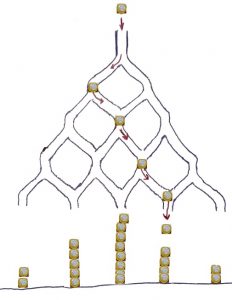	Même quantité de chocolat mais fondu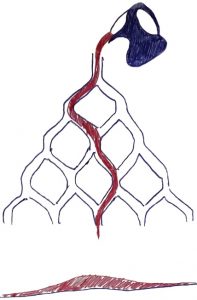
	Aires identiques

Figure 1. Illustration planche de Galton.↩

Des simulations informatiques confortent et affinent cette première impression. Plus précisément, suivons l’évolution de $f_n = \dfrac{S_n}{n}$, homogène à une fréquence. Le bon sens (et la loi des grands nombres) nous la font converger vers $p$. La variance étant ici additive, $E(f_n^2 ) = \dfrac{\sigma^2_n}{n}$ où $\sigma_n=pq$. La loi normale cible a donc pour densité de probabilité:

$$\frac{\exp \left(-\frac{1}{2} \left(\frac{x-p}{\sigma_n}\right)^2\right)
}{\sqrt{2\pi}\sigma_n}\cdotp$$

Pour contrôler le rapprochement des lois, il faut d’abord associer une densité de probabilité à la variable discrète $f_n$, en interprétant $\mathbb{P} \left(\dfrac{s_n}{n}=\dfrac{k}{n}\right)$ comme l’intégrale d’une constante sur l’étendue $\left[\dfrac{k}{n} ; \dfrac{k+1}{n}\right]$, ou, mieux (correction de continuité), sur $\left[\dfrac{k}{n}-\dfrac{1}{2n} ; \dfrac{k}{n}+\dfrac{1}{2n}\right]\cdotp$ C’est assimiler la densité de probabilité de $f_n$ à l’application en escalier valant $n\begin{pmatrix}n\\k\end{pmatrix} p^{n-k}q^{k}$ (le $n$ en facteur intègre l’étroitesse de la subdivision, la somme discrète totale valant 1) entre $\dfrac{k}{n} – \dfrac{1}{2n}$ et $\dfrac{k}{n} + \dfrac{1}{2n}\cdotp$ Le script Python en découle

from math import *import matplotlib.pyplot as plt
import random
import scipy
def VoirCentralLimite(p,n):
'''approximation continue de la loi discrète de Bernoulli'''
x = 0
sigma = sqrt(p*(1-p)/n)
Lx, Ly = [],[]
Gx, Gy = [],[]
for i in range(n+1):

Lx.append(x)

Gx.append(x)

Ly.append(n*scipy.misc.comb(n, i)*p**i * (1-p)**(n-i))

Gy.append((1/sqrt(2*pi*sigma**2))*exp(-((x-p)**2/(2*(sigma**2)))))

x = x + 1/n

Lx.append(x)
Ly.append(n*scipy.misc.comb(n, i)*p**i * (1-p)**(n-i))
plt.plot(Lx,Ly,'b-') #pour la loi de Bernoulli
plt.plot(Gx, Gy, 'r-') #pour le contour gaussien

À la commande VoirCentralLimite(0.3,100), l’ordinateur répond, très convaincant, la figure 2. Maintenant résolus à substituer une loi par l’autre nous affirmons avec raison que, pour les valeurs de $n$ « assez grandes », la probabilité que $f_n$ avoisine $p$ à $1,96\dfrac{\sigma_n}{\sqrt{n}}$ près frise les 95%.

Dès lors, à quelques rares exceptions près:
$$\left|f_n-p \right| \leqslant 1,96\frac{\sigma_n}{\sqrt{n}},$$
domaine plan dont le contour satisfait l’équation de l’ellipse d’incertitude

$$\left(f_n-p \right)^2 = 1,96 \frac{p(1-p)}{n}\cdotp$$

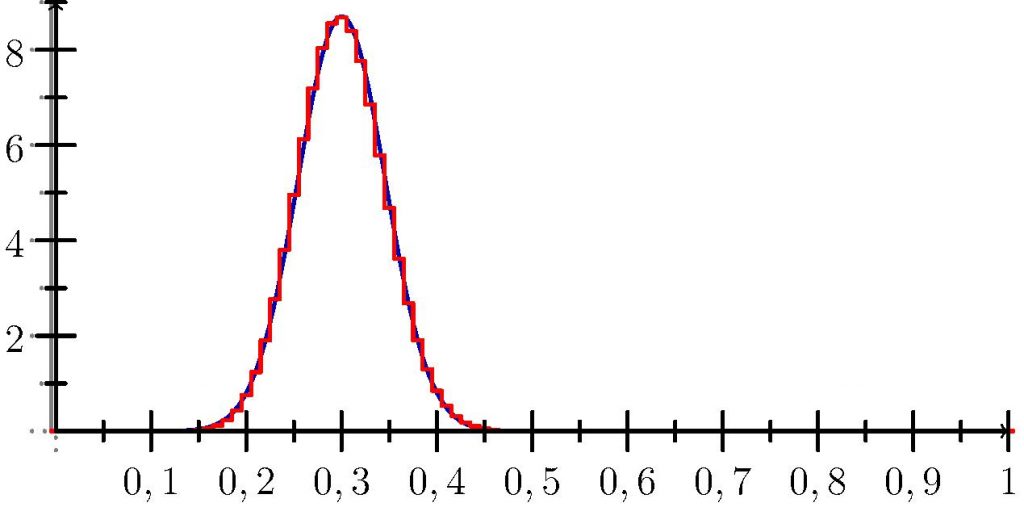
Figure 2. *Densités comparées de $ƒ_n$ et d’une gaussienne cible.*↩

Retrouvons cela par simulation.

Fixons $n$. Pour plusieurs valeurs de $p$, demandons chaque fois plusieurs valeurs de fréquence (qui nécessitent elles-mêmes, en filigrane, plusieurs tirages comme autant de pas d’une marche aléatoire).

Puis lançons l’instruction de tracé,

EllipseFluctuation(n=30,nTirages=100,pas=0.05).

Le nuage des points $(p ; f_n)$ est essentiellement bordé par une ellipse, frontière qu’il traverse à peine, figure 3, comme Tchernobyl !

def echantillon(p,n):

'''on simule une variable aléatoire de Bernoulli'''

succes = 0

for i in range(n):

if random.random() <= p:

succes = succes+1

f = succes /n return f

def EllipseFluctuation(n,nTirages,pas):

'''on discretise p au pas "pas" sur [0,1], en chacun on réalise

nTirages d'une expérience de Bernoulli de paramètres p,nTirages

on affiche les couples (p,f)

on trace le contour de l'ellipse d'incertitude'''

p = 0

Lx, Ly = [],[]

Exbas, Exhaut, Eybas, Eyhaut = [],[],[], []#pour contour

while(p<1):

for i in range(nTirages) :

Lx.append(p); Ly.append(echantillon(p,n))

sigma = sqrt(p*(1-p)/n)

Exbas.append(p); Exhaut.append(1-p-pas)#pour contour

Eybas.append(p-1.96*sigma) ; Eyhaut.append(p+1.96*sigma)#pour contour

p = p + pas

Eyhaut.reverse() #pour contour

Ex = Exbas + Exhaut; Ey = Eybas + Eyhaut #pour le contour

plt.plot(Lx,Ly,'b.')

plt.plot(Ex, Ey, 'r-') #pour contour

plt.plot()

plt.grid()

plt.show()

Pour $p$ (respectivement $f_n$) donné, l’excursion de la fréquence $f_n$ (resp. de la proportion $p$) est matérialisée par le segment vertical (resp. horizontal), dit intervalle de fluctuation (resp. de confiance). Aux coins, près desquels les tangentes à l’ellipse peuvent être parallèles aux axes, une faible variation de $p$ peut induire une forte variation du domaine de $f_n$, et vice-versa. La relation de liaison n’est donc pas robuste, cela explique qu’on n’exploite pas, en pratique, les extrémités. Ajoutons qu’à $f_n$ fixé, l’intervalle de confiance, ayant pour rayon $1,96\dfrac{\sigma_n}{\sqrt{n}} = 1,96\sqrt{\dfrac{p(1-p)}{n}}$, n’est pas connu. Pour déjouer le mystère, on remplace empiriquement le produit $p(1-p)$ par le produit $f_n(1-f_n$), qui l’estime, ou – c’est plus prudent – on le majore par $\dfrac{1}{4}\cdotp$ Comme $\dfrac{1,96}{\sqrt{4}} \leqslant 1$ on s’accommode volontiers de l’intervalle de confiance $
\left[f_n-\dfrac{1}{\sqrt{n}} ; f_n+\dfrac{1}{\sqrt{n}}\right]\cdotp$

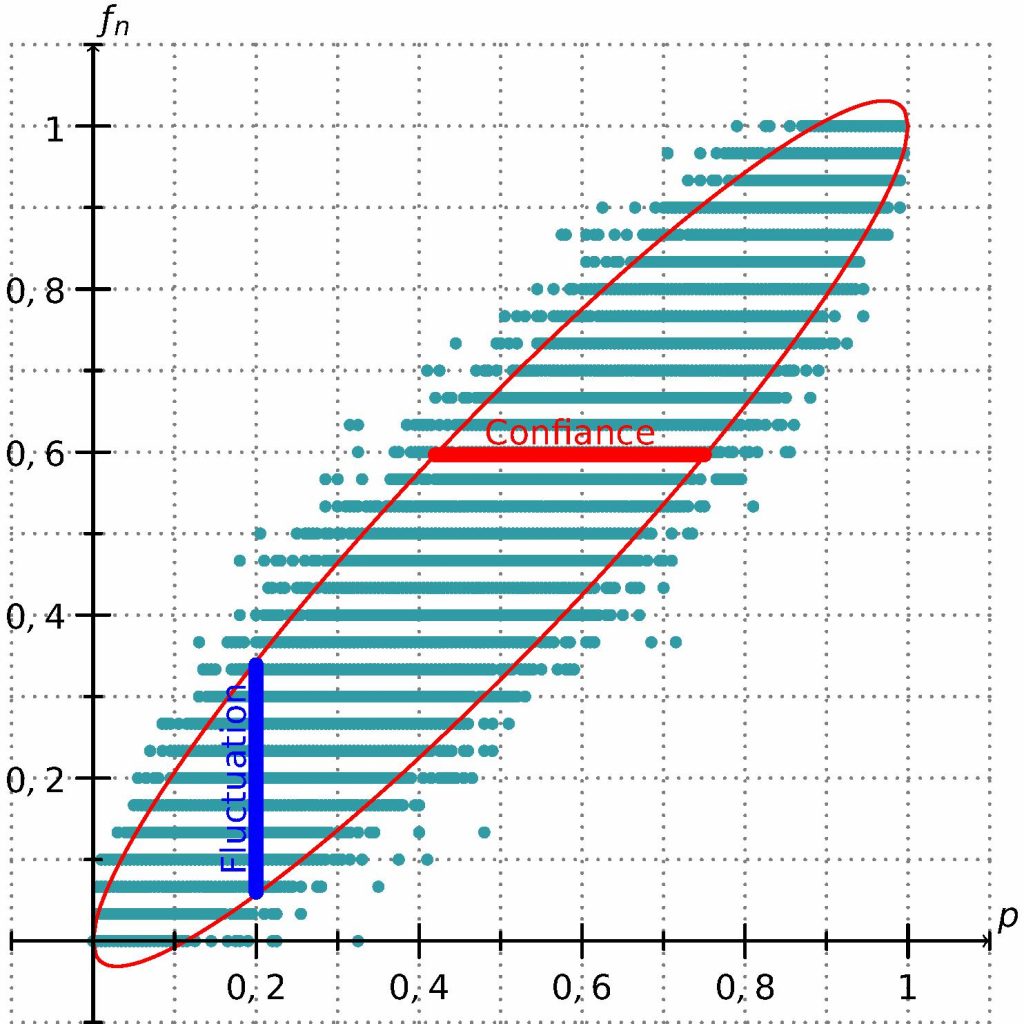
Figure 3. *Ellipse, confiance, fluctuation*.↩

Tablettes de chocolat : ce qu’en disent les lois

Le Baccalauréat aime également le chocolat (voir [5], [6], [7] ). Un scénario bien rodé : le fabricant Choko ne sait pas comment régler ses machines à tablettes de 100 grammes? Viens-lui en aide ! Le distributeur Aupré peut-il se fier à lui ? Rassure-le ! Tout est affaire de loi(s). . . Et en la matière, le décret 78-166 du 31 janvier 1978 relatif au contrôle métrologique des préemballages fixe des règles strictes :

une tablette de 100 grammes (nets, hors conditionnement: sans le papier d’aluminium donc) peut s’écarter légèrement de ce poids nominal. Il est reconnu que le poids⁵ de 100 g affiché sur l’emballage n’est qu’une « estimation », souvent symbolisée par la lettre « e » (figure 4);

Figure 4. Logo e. ↩
est tolérée une « erreur maximale » de 4,5 g, dans un sens précisé ci-après ;
dans un lot quelconque, la proportion de tablettes présentant une « erreur en moins » (appelée aussi « manquant ») inférieure à l’erreur maximale tolérée de 4,5 g doit être supérieure à 97,5 %. Ainsi, au moins 97,5 % des tablettes du lot pèsent au moins 95,5 g ;
aucune tablette défectueuse ne doit être super-défectueuse, c’est-à-dire présenter une erreur au moins double de l’erreur maximale : 9 g, sous peine de se voir retirer le label « e ». Ainsi, sous couleur d’étiquetage « e », aucune tablette ne pèse moins de 91 g ;
la moyenne des masses des tablettes du lot ne doit pas être inférieure à la quantité nominale annoncée: 100 g.

Mettons-nous à la place de l’industriel. Il ajustera sa chaîne de production, aux issues supposées gaussiennes, pour qu’en sortie les masses des tablettes répondent au cahier des charges : $m=100$ et $\sigma \leqslant \dfrac{4,5}{2} = 2,25$⁶. Les fabricants « low-cost » n’ont pas des machines précises, leur production est irrégulière en qualité (écart-type élevé). Si $\sigma >2,25$, ils sont contraints de fixer
$$m \geqslant 100 – 4,5 +2 \sigma$$
s’ils veulent se conformer à la législation française, selon les préconisations de la DGCCRF [2].

Mettons-nous à la place du commerçant qui a passé commande. Il réceptionne un lot de l’industriel. En extrait un échantillon de taille $n$. On suppose que l’échantillon est assez petit et le lot assez grand pour que les tirages, pourtant sans remise, soit considérés comme non exhaustifs. On calcule la fréquence $f_n$ de tablettes conformes, on la situe par rapport à l’intervalle de fluctuation attendu au seuil de 95 %. C’est la sempiternelle question:
$$f_n \in \left[p -1,96 \sqrt{\frac{p(1-p)}{n}}\;;\;
p+1,96 \sqrt{\frac{p(1-p)}{n}}\right]\ ?$$
avec $p = 97,5$ %.

Mettons-nous à la place du candidat. Il le remarquera peut-être : le sujet aura souvent choisi pour l’industriel un intervalle de mise sur le marché qui est centré (et non monolatéral). Il le notera également : l’énoncé ne dit jamais ce qu’il advient des tablettes test – en particulier qui les mange. Une fois l’épreuve terminée, gageons qu’il sortira du sac une barre de céréales.

L’auteur tient à remercier Edwige Croix et François Bouyer pour leur relecture attentive.

Karim Zayana est inspecteur général et professeur invité à l’Institut Mines-Télécom. Cet article fait suite à plusieurs échanges avec les équipes des professeurs des établissements d’Ajaccio, de Corte, de Reims, avril-octobre 2017.

Références

Tim Burton. Charlie et la Chocolaterie. 2005. ↩
DGCCRF. Métrologie et transaction commerciale. 4 fév. 2018. ↩
Richard Isaac. Une initiation aux probabilités. Trad. par Roger Mansuy. Paris : Vuibert, Springer, 2005. ↩
Daniel Perrin. « Remarques sur l’enseignement des probabilités et de la statistique au lycée ». In : Statistique et Enseignement6.1 (2015). ↩
Série L, Amérique du nord. 2010. ↩
Série S, Amérique du nord. 2015. ↩
Série S, Pondichéry. 2017. ↩
Charles Torossian. Du jeu de Pile ou Face à la formule de Black and Scholes. 2013. ↩
Robert Zemeckis. Forrest Gump. 1994. ↩

Et les crevettes. ↩
Multiplier le développement de $\dfrac{1}{1-p}$ vu plus haut par lui-même, ou le dériver terme à terme pour obtenir la formule désirée. ↩
D’autres modèles ont l’apparence d’un billard. ↩
On considère ici que la pièce et la nappe ont même épaisseur. ↩
La masse, en toute rigueur. ↩
95 % des réalisations d’une variable aléatoire normale sont concentrées sur $\left[m-2\sigma ;m+2 \sigma\right]$, et 97,7 % sur $\left[m-2\sigma ; + \infty \right[$ (où l’on a arrondi 1,96 en 2 dans les intervalles, centré et unilatéral). ↩

Pour citer cet article : Zayana K., « Pas de probas, pas de chocolat ! », in APMEP Au fil des maths. N° 527. 6 avril 2018, https://afdm.apmep.fr/rubriques/ouvertures/pas-de-probas-pas-de-chocolat/.