L’arithmétique en jouant
« Les enfants n’ont point d’affaires plus sérieuses que leurs jeux » écrivait Montaigne. Une fois encore, Jean Fromentin nous fait faire des mathématiques en jouant et c’est un plaisir de le suivre. . . au crayon ou à la souris !
Jean Fromentin
© APMEP Mars 2018
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
C’est un des premiers jeux que j’ai utilisé en classe, donc à des fins d’apprentissage. Dans les années 70, l’arithmétique avec les multiples, diviseurs, pgcd, ppcm était au programme en 6e et en 5e. Et, après avoir offert ce Spirograph à mes enfants, j’ai vu tout de suite le profit pédagogique que je pouvais en tirer.
La fiche d’activité que j’avais réalisée à cette époque est publiée dans la brochure JEUX 5 de l’APMEP, que vous pouvez encore vous procurer.
Le principe de ce jeu est de dessiner des lignes avec des roues dentées qui tournent contre d’autres engrenages. On devine qu’il s’agit d’épicycloïdes et d’hypocycloïdes; mais de telles courbes n’étaient tout de même pas un objet d’étude à ce niveau-là!


Figure 1. Le Spirograph.
Ce jeu de plus de 60 ans est toujours commercialisé, mais la composition des boîtes au niveau des roues dentées peut varier d’une édition à l’autre. Aussi, les roues utilisées dans l’activité peuvent ne pas figurer dans les boîtes de jeu à votre disposition. Je possédais six jeux pour une classe d’environ 24 élèves. Deux tables rapprochées recevaient un jeu pour un groupe de quatre élèves.
Voici l’ensemble des roues dentées que comportaient les boîtes. Sur chaque roue est inscrit son nombre de dents. Mais j’avais collé de petites étiquettes, indiquant le nombre de dents, à côté de chaque roue pour faciliter le repérage des roues à utiliser. Ces numéros sont les suivants : 24, 30, 32, 36, 40, 42, 45, 48, 50, 52, 56, 60, 63, 64, 72, 75, 80, 84, 144 et 150 ; 96 et 105 pour l’intérieur des couronnes.
Pour les tracés, les roues étaient fixées, à cette époque, sur un carton épais par de petites épingles. Dans les nouvelles éditions, ces petites épingles n’existent plus pour des raisons de sécurité, ce qui ne facilite donc pas le tracé.

Figure 2. Deux épingles, un stylo fin et c’est parti !↩
L’exercice de base consiste à placer une feuille (blanche) sur le carton, d’y fixer une roue (roue fixe), de poser contre elle une roue mobile, de positionner un crayon dans l’un des trous de la roue mobile et de tracer une ligne en faisant tourner la roue mobile autour de la roue fixe et en gardant sans cesse le contact entre les deux roues.
Le Spirograph : un jeu numérique ?
La question peut paraître incongrue vu le thème abordé par la pratique de ce jeu. Mais le mot numérique désigne aussi la possibilité d’utiliser les écrans numériques. Et BINGO! Ce jeu peut être aussi pratiqué sur ordinateur. Un immense merci à Nathan Friend qui a transposé à l’identique l’ensemble des éléments du Spirograph car je ne vous dis pas le nombre de ratés que j’ai rencontrés pour les dessins de cet article, essentiellement dus au fait que la roue mobile se décroche un peu trop facilement de la roue fixe.
Nathan Friend a donc été bien inspiré d’en faire un jeu numérique appelé, comme il se devait, Inspirograph ! Pour l’instant, ce matériel est utilisable uniquement en ligne sur le site. N’hésitez pas à l’utiliser au fil de la lecture de cet article. Tout ce que vous pourrez y lire dans est donc réalisable de façon ô combien plus simple !
Rappelons qu’un jeu utilisé en classe de mathématiques, même s’il a un caractère ludique, doit amener les élèves, par sa pratique, à progresser dans leur savoirs et savoir-faire mathématiques. De plus, ici, l’étude mathématique du jeu a des retombées certaines sur son utilisation ludique.
Observations, manipulations
Avant de se lancer dans l’activité, il faut bien sûr que les élèves prennent connaissance du matériel ou du logiciel en ligne. C’est l’occasion de leur laisser un peu de liberté dans l’utilisation du jeu, ce qui leur permettra de mieux rentrer dans l’activité proprement dite.

Figure 3. Accentuation des points de rebroussements.
Il est important que les élèves acquièrent une certaine dextérité pour la suite de l’activité, surtout que la consigne est de mettre le crayon dans le trou le plus près du bord de la roue mobile (voir la figure [2]).
En effet, en plaçant le crayon ainsi, on accentue le dessin des boucles et on peut ainsi mieux les repérer. Les minima (points les plus près de la roue fixe) correspondent aux points de rebroussement d’une épicycloïde.
Dans la suite, nous mettrons en caractère gras le numéro de la roue fixe et en italique celui de la roue mobile.
La figure 4 est une copie de la feuille de dessin du logiciel.
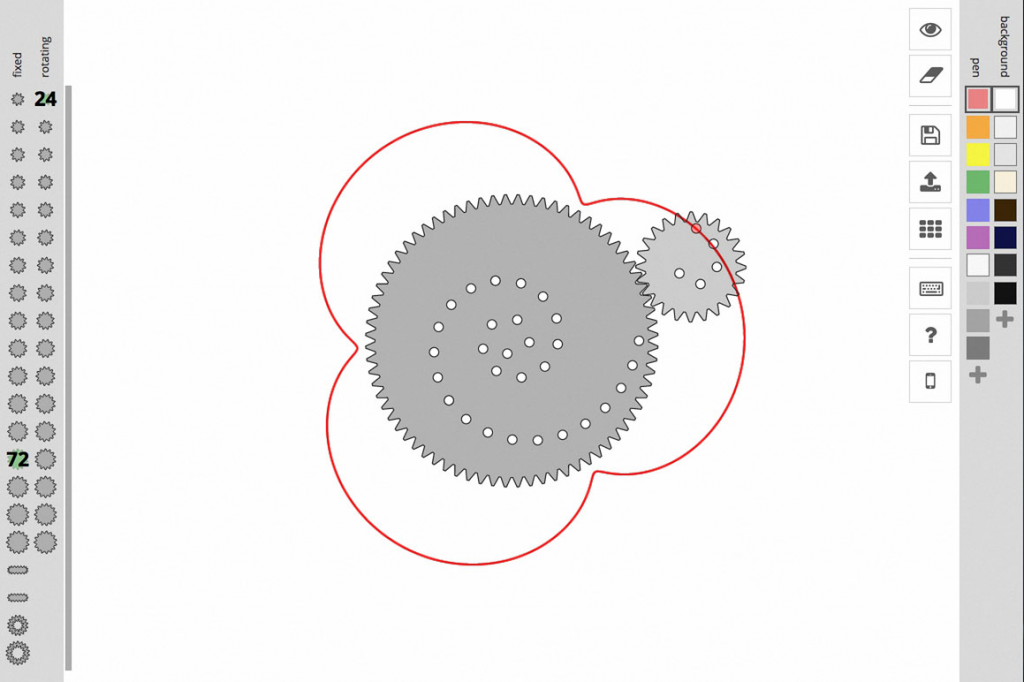
Figure 4. Inspirograph.
Par des clics de souris, on choisit dans les deux colonnes de gauche la roue fixe et la roue mobile, puis le trou de la roue mobile dans lequel on veut mettre le crayon. Un clic appuyé sur la roue mobile enclenche le dessin en déplaçant la souris dans un sens ou dans l’autre. En passant et repassant sur le dessin, le tracé est un peu plus accentué. On peut changer la couleur du crayon, celle de la feuille de dessin, cacher les roues, effacer le dessin. Vivement que cette application soit disponible sur tablette !
Une première notion : la division euclidienne
Prenons le couple (56 ; 24) et faisons faire à la roue mobile une révolution autour la roue fixe, donc sans dépasser la position initiale de la roue mobile. Dans ce cas, on a dessiné deux boucles entières et un morceau de boucle.

Figure 5. Le quotient et reste.
Les deux boucles entières correspondent à 2 × 24 dents et le morceau de boucle au reste de dents sur la roue fixe. On a bien une situation de division euclidienne : le nombre de dents de la roue fixe est le dividende, le nombre de dents de la roue mobile est le diviseur et le nombre de boucles entières est le quotient.
Si la courbe ne se referme pas exactement en fin de révolution, le nombre de dents qui restent entre les deux minima extrêmes est le reste. Si la courbe se referme exactement, le reste est alors nul.
À l’issue de cette première expérience, on peut proposer aux élèves, à l’aide d’un vidéoprojecteur, une série de petits problèmes sur la division euclidienne tel celui de la figure [6].
Le seul renseignement évident est le nombre de boucles entières, c’est-à-dire le quotient. On leur indique alors deux des trois renseignements manquants et ils doivent trouver le troisième. Par exemple, ici, en leur indiquant que la roue fixe a 150 dents (dividende) et qu’il reste 6 dents à la roue mobile pour finir sa révolution, ils devront trouver le diviseur (nombre de dents de la roue mobile). Suivant les renseignements donnés, une telle image est donc à la base de trois petits problèmes.

Figure 6. Une image, trois problèmes.↩
Multiples et diviseurs
Ce jeu permet donc de matérialiser, par les tracés, les notions de multiples et de diviseurs. Si la courbe se referme exactement au bout d’un tour, en dessinant par exemple trois boucles, alors le nombre de dents de la roue fixe est égal au triple du nombre de dents de la roue mobile. La figure [7] montre le couple de roues (72 ; 24).
On peut alors demander aux élèves de repérer tous les couples de roues dont les numéros sont multiples ou diviseurs l’un de l’autre et de donner tous les couples à 2 boucles, tous ceux à 3 boucles, 4 boucles…
Avec quels couples de roues obtient-on le maximum de boucles?

Figure 7. Multiples et diviseurs : (72 ; 24).↩
Multiples communs
Si on fait tourner la roue mobile de 40 dents autour de la roue fixe de 50 dents jusqu’à ce que la courbe se referme, la roue mobile a dessiné 5 boucles (repérés facilement par les 5 minima) en faisant 4 révolutions autour de la roue fixe. Le nombre total de dents parcourues sur la roue fixe (50 × 4) est égal au produit du nombre de dents de la roue mobile par le nombre de boucles (40 × 5). Ce nombre, 200, est donc à la fois multiple de 40 et de 50, et c’est le plus petit non nul ; c’est donc le PPCM de 40 et de 50.

Figure 8. PPCM de 40 et 50.
Comme pour la division euclidienne, on peut proposer aux élèves des séries de situations comme celle de la figure [9]. On observe qu’il y a 3 minima, donc 3 boucles et 2 révolutions de la roue mobile autour de la roue fixe. En donnant le nombre de dents de l’une des deux roues, les élèves doivent trouver le nombre de dents de l’autre roue. Ici, la roue fixe possède 84 dents. Comme il y a deux révolutions, la roue mobile a parcouru 2 × 84 dents, soit 168 dents. Comme elle a tracé 3 boucles, elle possède donc 168 ÷ 3 dents, soit 56 dents.
Même si la notion de PPCM n’est pas dans les programmes, il n’est pas interdit de faire cette activité. Pour des nombres simples, on rencontre déjà cette notion à propos des fractions à mettre au même dénominateur.

Figure 9. Combien de dents ?↩
Nombres premiers entre eux
Dans l’exemple du couple de roues (50 ; 40), on peut remarquer que les 5 minima sont répartis régulièrement sur la roue fixe et donc qu’ils sont toutes les 10 dents ; on observe que 10 est le PGCD de 40 et de 50 !
Dans l’exemple du couple de roues (84 ; 56), on peut remarquer que les 3 minima sont répartis régulièrement sur la roue fixe et donc les minima sont toutes les 28 dents ; on observe aussi que 28 est le PGCD de 56 et de 84 !
Si m désigne le nombre de minima sur la roue fixe et r le nombre de révolutions de la roue mobile autour de la roue fixe, on a la formule suivante: PPCM = PGCD × m × r.
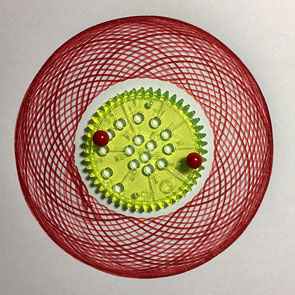
Figure 10. Multiples et diviseurs : (45 ; 32).↩
Dans l’exemple de la figure [10] (situation difficile à dessiner vu le grand nombre de boucles à tracer), avec le couple de roues (45 ; 32), les minima sont à chaque dent de la roue fixe. La roue mobile a donc fait 45 boucles et 32 révolutions autour de la roue fixe. Le PPCM est donc 45 × 32 et le PGCD est 1. Les nombres 45 et 32 sont en effet premiers entre eux.
Des tracés semblables, des fractions égales
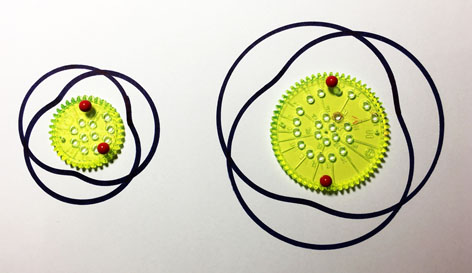
Figure 11. Des fractions ? Où ça ?↩
Les deux tracés de la figure [11] ont les mêmes nombres de minima (m = 3) et de révolutions (r = 2). Les deux couples de roues choisies ici sont (36 ; 24) et (60 ; 40). Ces deux couples de nombres sont dans la même proportion \(\dfrac{2}{3}\) , soit \(\dfrac{r}{m}\cdotp\) Ces tracés semblables désignent donc des fractions égales, la fraction réduite étant \(\dfrac{r}{m}\cdotp\)
On peut aussi remarquer que le deuxième dessin est un agrandissement du premier dans le rapport \(\dfrac{60}{36}\), soit \(\dfrac{5}{3}\cdotp\)
Voici les couples de roues correspondant à quelques fractions choisies :
\(\dfrac{1}{2}\) : (84 ; 42), (80 ; 40), (72 ; 36), (64 ; 32), (60 ; 30), (48 ; 24) ;
\(\dfrac{1}{3}\) : (72 ; 24) ;
\(\dfrac{2}{3}\) : (84 ; 56), (75 ; 50), (72 ; 48), (63 ; 42), (60 ; 40), (48 ; 32), (45 ; 30), (36 ; 24) ;
\(\dfrac{3}{4}\) : (84 ; 63), (80 ; 60), (64 ; 48), (60 ; 45), (56 ; 42), (48 ; 36), (40 ; 30), (32 ; 24) ;
\(\dfrac{2}{5}\) : (80 ; 32), (75 ; 30), (60 ; 24) ;
\(\dfrac{3}{5}\) : (80 ; 48), (75 ; 45), (60 ; 36), (50 ; 30), (40 ; 24).
Pour aller plus loin
Dans tous les tracés que nous avons effectués, la roue mobile avait toujours un nombre de dents plus petit que celui de la roue fixe. Et si on inversait les rôles ? Voici donc cette fois les couples de roues (40, 50) à gauche et (56, 84) à droite.
Pour le couple de roues (40, 50), la roue mobile a tracé 4 boucles et a donc parcouru 4 x 50 dents tout en faisant 5 révolutions, soit 5 x 40 dents. On retrouve le PPCM de 40 et de 50, mais le nombre de boucles est devenu le nombre de révolutions et inversement.

On observe bien sûr le même phénomène pour le couple de roues (56, 84). La roue mobile a tracé 2 boucles sur la roue fixe et a fait 3 révolutions.

Le nombre de dents qui séparent deux minima (40 : 4 = 10 pour le couple (40, 50) et 56 : 2 = 28 pour le couple (56, 84)) est bien le PGCD des deux nombres considérés.
On observe donc qu’en inversant roue fixe et roue mobile on inverse aussi le nombre de boucles et le nombre de révolutions et, bien sûr, la formule PPCM = PGCD x m x r reste vraie.
Des épicycloïdes aux hypocycloïdes
Jusqu’à présent, nous n’avons rencontré que des épicycloïdes, cercle mobile tournant à l’extérieur contre le cercle fixe. Le jeu du Spirograph ne nous donne pas beaucoup de choix pour réaliser des hypocycloïdes, cercle mobile tournant à l’intérieur contre le cercle fixe. Seuls les anneaux de 96 et de 105 dents sont disponibles.
Voici deux tracés qui permettent d’imaginer ce que l’on peut proposer aux élèves.

Avec le couple (96, 32) on obtient un « triangle » et avec le couple (105, 42), un « pentagone étoilé ».
96 = 32 x 3. La roue mobile trace donc 3 boucles en une seule révolution.
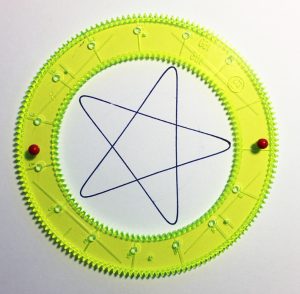
105 = 3 x 5 x 7 et 42 = 2 x 3 x 7. Le PGCD de ces deux nombres est 21. De ce fait, Les minima sur la roue fixe sont séparés de 21 dents. Il y aura donc 5 minima qui formeront un pentagone étoilé.
L’activité des élèves peut donc consister à trouver, avec les anneaux de 96 et de 105 dents, tous les couples qui permettent d’obtenir des « polygones convexes » et des « polygones étoilés ».
Une remarque concernant le couple (96, 48) : le rayon du disque mobile est égal à la moitié de celui de l’anneau fixe. Dans le cas des cercles, un point du cercle mobile parcourt un diamètre du cercle fixe. Ici, comme le trou dans lequel on place le crayon n’est pas exactement sur la circonférence, on obtient un ovale très aplati comme sur la photo ci-dessous.

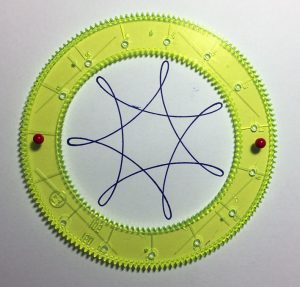
Considérons les couples (105, 30) et (105, 45).
105 = 3 x 5 x 7, 30 = 2 x 3 x 5 et 45 = 3 x 3 x 5. Pour ces deux couples, le PGCD est 15 et donc, dans les deux tracés, les minima seront séparés de 15 dents. On obtient donc deux heptagones étoilés. Si on avait une roue de 15 dents, on obtiendrait un heptagone convexe (les minima sur la roue fixe seraient consécutifs. La roue de 30 dents (30 = 2 x 15) donne un heptagone étoilé dont les minima consécutifs vont de deux en deux puisque séparés de 30 dents ; dans l’heptagone obtenu avec la roue de 45 dents (45 = 3 x 15), les minima consécutifs vont de trois en trois. 
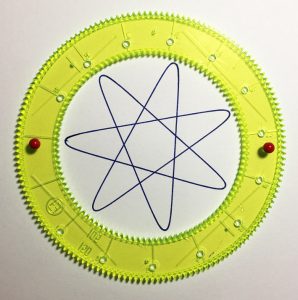
15, 30, 45… et avec les roues de 60 et de 75 dents ? On obtient toujours sept minima qui vont successivement de quatre en quatre (de trois en trois dans l’autre sens) et de cinq en cinq (de deux en deux dans l’autre sens).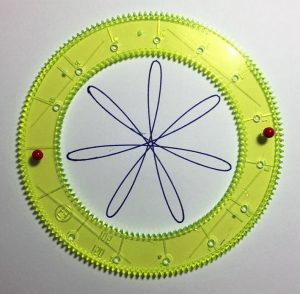
La roue de 90 dents donnerait un heptagone « presque convexe » puisque chaque sommet serait formé d’une petite boucle.
On devine combien il est intéressant de trouver les PGCD des couples de roues (105, n) et (96, p) et donc de décomposer en facteurs premiers tous les nombres de dents des roues du Spirograph.
Le tableau ci-dessous indique le nombre de minima obtenus par les roues à l’intérieur des anneaux à 105 ou 96 dents.
On peut ainsi connaître le nombre de « branches » du dessin et la taille des boucles suivant la distance entre les minima consécutifs.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voici un exemple avec les trois couples (96, 36), (96, 60), (96, 84), dans l’ordre des photos, qui donnent un dessin de 8 boucles. Plus le nombre de dents de la roue mobile est grand, plus les boucles sont petites.


Alors ! Spirograph ou Inspirograph … à vous de jouer !

