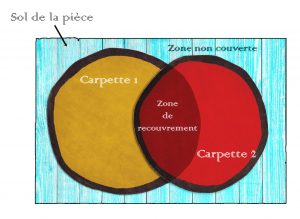
Le théorème des carpettes
Voici un théorème de géométrie élémentaire au drôle de nom, qui va nous faire aller de surprise en surprise ! Découvrons avec Yves Farcy ses applications originales joliment illustrées. Un bon moment garanti !
Yves Farcy
© APMEP Mars 2021
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
C’est en me perdant sur le site cut-the-knot du regretté Alexandre Bogomolny que j’ai, pour la première fois, rencontré ce très joli théorème. Il semblerait que ce soient Titu Andreescu et Bogdan Enescu qui, en 2004, dans un ouvrage sur les Olympiades de mathématiques [1], utilisent pour la première fois le mot de carpette pour désigner le théorème. Il est proposé comme une démonstration élégante de l’exemple 1 ci-dessous.
Le théorème des carpettes
Je présente ici un énoncé possible de ce théorème, un peu différent de celui que propose Alexandre Bogomolny .
| Théorème des carpettes |
|
Soient deux carpettes étalées sur le sol d’une pièce.
|
Preuve
Les deux carpettes étant incluses dans le sol de la pièce, on a :
\(
\text{Aire(sol de la pièce)}=\text{Aire(non couv.)}+\text{Aire(Carpette 1)}
+\text{Aire(Carpette 2)}-\text{Aire(recouvrem.)}\)
Et donc :
\(\text{Aire(sol de la pièce)}=\text{Aire(Carpette 1)}+\text{Aire(Carpette 2)}
\Leftrightarrow\text{Aire(non couv.)}=\text{Aire(recouvrem.)}\)
Applications à la géométrie
-
Montrer l’égalité entre l’aire de la surface bleue et la somme des aires des surfaces jaunes dans le rectangle \(\mathsf{ABCD}\).
Solution
Les deux carpettes sont les triangles \(\mathsf{ABE}\) et \(\mathsf{ADF}\). \(\mathsf{ABE}\) a la même base et la même hauteur et donc la même aire que \(\mathsf{ABD}\) soit la moitié du rectangle \(\mathsf{ABCD}\). Il en va de même pour \(\mathsf{AFD}\).
On a donc
\(\text{Aire}(\mathsf{ABE})+\text{Aire}(\mathsf{AFD})=\text{Aire}(\mathsf{ABCD})\) et on peut appliquer le théorème des carpettes avec \(\text{Aire(non
couverte)}=\text{Aire}(\mathsf{FGB})+\text{Aire}(\mathsf{EHFC})+\text{Aire}(\mathsf{DIE})\)
et \(\text{Aire(recouvrement)}=\text{Aire}(\mathsf{AIHG})\) et donc\(\text{Aire}(\mathsf{AIHG})=\text{Aire}(\mathsf{FGB})+\text{Aire}(\mathsf{EHFC})+\text{Aire}(\mathsf{DIE})\)
soit
\(\text{Aire(surface bleue)}=\text{Aire(surfaces jaunes)}\)
-
Des amandes et des parapluies
.
Montrer que l’aire des amandes (en vert) est égale à l’aire des parapluies (en lavande), quelle que soit la position des points de tangence \(\mathsf{A}\) et \(\mathsf{B}\).
Solution
On définit le sol et les deux carpettes :
Si \(R\) est le rayon des deux disques constituant chaque carpette, le sol a pour rayon \(2R\). Ainsi \(\text{Aire(sol)}=4\pi R^2\) et \(\text{Aire(carpette
1)}=\text{Aire(carpette 2)}=2\pi R^2\) et donc \(\text{Aire(sol)}=\text{Aire(carpette 1)}+\text{Aire(carpette 2)}\) et donc, d’après le théorème des carpettes, l’aire des amandes est égale à l’aire des parapluies.Vous pourrez trouver sur le site
cut-the-knotd’autres exemples d’application. Mais on peut se laisser aller à son imagination pour trouver d’autres situations. Je vous en propose trois originales. -
Ouverture des parapluies ou deux dodécagones réguliers inscrits dans un rectangle.
Montrer que l’aire de la surface verte est égale à l’aire de la surface orange.
Solution
Si on appelle \(R\) le rayon du cercle circonscrit d’un dodécagone, l’aire de chaque dodécagone régulier est \(3R^2\). On choisit les dimensions du rectangle pour que son aire soit \(6R^2\), par exemple \(2R\) et \(3R\).
La somme des aires des dodécagones est donc égale à l’aire du rectangle. On peut alors appliquer le théorème des carpettes : l’aire de la surface verte (surface de recouvrement) est donc égale à l’aire de la surface orange (surface non couverte).
Ce raisonnement est valable quelle que soit la position des dodécagones dans le rectangle : les valeurs des aires changent mais l’égalité reste vraie !
-
Lavande et capucine.
Les différents rayons des cercles sont dans un ratio 1 : 2 : 3 : 4. Montrer que l’aire des surfaces capucine est égale à l’aire des surfaces lavande.
La solution est laissée au lecteur.
-
La « même idée » dans l’espace puisque le théorème s’étend aux volumes.
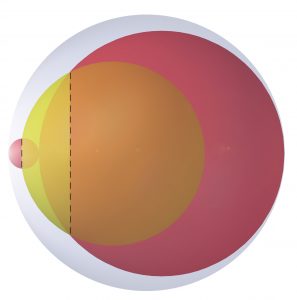
Les deux boules rouges sont tangentes entre elles et tangentes à la boule bleue.
Les différents rayons des boules sont dans un ratio 1 : 6 : 8 : 9. Montrer que le volume de l’intersection de la boule jaune et des deux boules rouges est égal au volume non occupé de la boule bleue.
La solution est laissée au lecteur.
Un détour par les probabilités
Voici l’énoncé du théorème appliqué aux probabilités.
| Théorème |
|
On se place dans un espace probabilisé. Soit \(\mathsf{\Omega}\) l’univers, \(\mathsf{A}\) et \(\mathsf{B}\) deux évènements sur cet univers. \(p(\mathsf{A}\cap\mathsf{B})=p(\overline{\mathsf{A}}\cap\overline{\mathsf{B}})\Longleftrightarrow p(\mathsf{A})+p(\mathsf{B})=1.\)
|
Preuve
On a :
\[\begin{aligned}
p(\mathsf{\Omega})&=p(\mathsf{A}\cup\mathsf{B})+p(\overline{\mathsf{A}\cup\mathsf{B}})\\
&=p(\mathsf{A})+p(\mathsf{B})-p(\mathsf{A}\cap\mathsf{B})+
p(\overline{\mathsf{A}}\cap\overline{\mathsf{B}})\\
&=1.\end{aligned}\]
Et donc :
\[p(\mathsf{A}\cap\mathsf{B})=p(\overline{\mathsf{A}}\cap\overline{\mathsf{B}})\Longleftrightarrow p(\mathsf{A})+p(\mathsf{B})=1.\]
Un exemple
Une urne contient \(20\) boules indiscernables au toucher numérotées de \(1\) à \(20\). des boules sont bleues, les autres rouges. On tire une boule au hasard.
Montrer que la probabilité de tirer une boule bleue portant un nombre premier est égale à la probabilité de tirer une boule rouge ne portant pas un nombre premier.
Solution
On assimile les boules à leurs numéros. On définit \(\mathsf{\Omega}=\{1 ;2 ;\dots ;20\}\), on choisit comme tribu \(\mathscr{A}=\mathscr{P}(\mathsf{\Omega})\) et \(p\) la probabilité uniforme.
Soit \(\mathsf{B}\) l’événement « la boule est bleue » et \(\mathsf{Pr}\) l’évènement « la boule est marquée d’un nombre premier ». Il y a huit nombres premiers entre \(1\) et \(20\) donc \(p(\mathsf{Pr})={0,4}\) et \(p(\mathsf{B})={0,6}\).
\(p(\mathsf{Pr})+p(\mathsf{B})=1\), on peut donc appliquer le théorème des carpettes : \(p(\mathsf{B}\cap\mathsf{Pr})=p(\overline{\mathsf{B}}\cap\overline{\mathsf{Pr}})\).
Ce qui est le résultat demandé.
Irrationalité de \(\sqrt{2}\)
C’est John Conway qui, dans le chapitre The power of mathematics d’un ouvrage collectif, cite cette belle preuve qu’il attribue à Stanley Tennenbaum. Vous trouverez par ailleurs dans ce chapitre sa preuve élégante du théorème de Morley et un joli paragraphe sur les nœuds [2].
John Conway ne parle pas explicitement du théorème des carpettes mais nous pouvons ici le voir opérer.
Supposons donc que \(\sqrt{2}\) soit rationnel.
Il existe donc un couple d’entiers \((a,b)\in(\mathbb{N}^{\ast})^2\) tels que \(\sqrt{2}=\dfrac{a}{b}\) et \(a\wedge b=1\).
\(a\) et \(b\) sont donc les plus petits entiers possibles.
Il vient \(a^2=2b^2\).
De plus comme \(1< \sqrt{2}< 2\), on a
\[b< a< 2b
\label{farcy_equa_1}\]
On construit maintenant un sol carré de côté \(a\) et on y place deux carpettes carrées de côté \(b\) comme sur la figure ci-dessous.
Comme \(b< a\) on est assuré que les deux carpettes sont incluses dans le carré de côté \(a\) et, du fait que \(b> \dfrac{a}{2}\), les deux carpettes ont une surface de recouvrement qui est un carré de côté \(2b-a\) ; la surface non recouverte est constituée de deux carrés de côté \(a-b\).
Comme \(a^2=b^2+b^2\), on peut appliquer le théorème des carpettes !
On a donc \((2b-a)^2=2(a-b)^2\) et un nouveau couple d’entiers naturels non nuls \(2b-a\) et \(a-b\) respectivement strictement plus petit que \(a\) et \(b\) d’après (1) et tels que \(\sqrt{2}=\dfrac{2b-a}{a-b}\cdotp\)
D’où la contradiction.
Irrationalité de \(\sqrt{3}\)
Forcément, lorsqu’on voit un tel résultat, on a envie d’essayer avec \(\sqrt{3}\). Au début, je ne voyais vraiment pas comment m’en sortir et placer trois carrés de côté \(b\) dans le carré de côté \(a\). Et puis…
Supposons donc que \(\sqrt{3}\) soit rationnel.
On définit \(a\) et \(b\) comme précédemment et il vient \(a^2=3b^2\).
Ici, on a besoin d’un deuxième encadrement \(\dfrac{3}{2}<\sqrt{3}<3\) (que l’on déduit de \(1<\sqrt{3}<2\) par passage à l’inverse), et en remplaçant \(\sqrt{3}\) par \(\dfrac{a}{b}\) on obtient
\[\begin{aligned}
3b&<2a\label{farcy_equa_2}\\
\text{et }3b&>a\label{farcy_equa_3}\end{aligned}\]
L’astuce est de déplacer la surface de recouvrement de deux carpettes carrées de côté \(b\) afin de ne pas avoir trois « épaisseurs ». Ceci est possible puisque \(2b-a<a-b\) d’après (2) ; qui plus est, l’aire de la surface obtenue est \(2b^2\).
Et maintenant tout s’enchaîne : l’aire du sol est \(\mathscr{A}_{\text{sol}}=a^2\).
L’aire de la première carpette est \(\mathscr{A}_1=2b^2\) et l’aire de la seconde carpette \(\mathscr{A}_2=b^2\). Maintenant on a : \(\mathscr{A}_{\text{sol}}=\mathscr{A}_1+\mathscr{A}_2\) et on peut appliquer le théorème des carpettes !
Déterminons maintenant l’aire de recouvrement \(\mathscr{A}_{\text{r}}\) et l’aire non couverte \(\mathscr{A}_{\text{nc}}\).
\[\begin{aligned}
\mathscr{A}_{\text{r}}&=b^2-(a-b)^2=a(2b-a)\\
\mathscr{A}_{\text{nc}}&=(a-b)^2-(2b-a)^2=b(2a-3b).\end{aligned}\]
Le théorème des carpettes nous assure alors que \(\mathscr{A}_{\text{r}}=\mathscr{A}_{\text{nc}}\) et donc que \(a(2b-a)=b(2a-3b)\). Nous y voilà, on a donc : \(\dfrac{a}{b}=\dfrac{2a-3b}{2b-a}\) avec \(0<2a-3b<a\) et \(0<2b-a<b\) grâce à (2) et (3), d’où la contradiction.
Irrationalité de \(\sqrt{5}\)
Le raisonnement suivant donne les idées pour la généralisation.
On a
\[2<\sqrt{5}<3\label{farcy_equa_4}\]
et par passage à l’inverse
\[\frac{5}{3}<\sqrt{5}<\frac{5}{2}\label{farcy_equa_5}\]
On utilise bien sûr le raisonnement par l’absurde : comme précédemment \(a^2=5b^2\) et en remplaçant \(\sqrt{5}\) par \(\dfrac{a}{b}\) dans (4) on obtient
\[2b<a\label{farcy_equa_6}\]
On va donc placer nos carrés de côté \(b\) dans notre carré de côté \(a\). On crée la première carpette avec quatre carrés de côté \(b\), placés dans chaque coin. Ces carrés ne se recouvrent pas car, d’après (6), \(2b<a\) et la largeur de l’espace non couvert entre deux carrés est \(a-2b\).
On dispose tout simplement le cinquième carré qui sera la seconde carpette sur un des quatre premiers.
La somme des aires des deux carpettes est bien égale à l’aire du sol donc l’aire de recouvrement \(\mathscr{A}_{\text{r}}\) est égale à l’aire non couverte \(\mathscr{A}_{\text{nc}}\).
\[\begin{aligned}
\mathscr{A}_{\text{r}}&=b^2\\
\mathscr{A}_{\text{nc}}&=a(a-2b)+2b(a-2b)\\
\mathscr{A}_{\text{r}}=\mathscr{A}_{\text{nc}}
&\Longleftrightarrow b^2=a(a-2b)+2b(a-2b)\\
&\Longleftrightarrow b^2=a(a-2b)+2ba-4b^2\\
&\Longleftrightarrow 5b^2-2ba=a(a-2b)\\
&\Longleftrightarrow b(5b-2a)=a(a-2b)\end{aligned}\]
Et donc : \(\dfrac{a}{b}=\dfrac{5b-2a}{a-2b}\) avec \(0<5b-2a<a\) d’après (5) et \(0<a-2b<b\) d’après (4) d’où la contradiction.
Généralisation irrationalité de \(\sqrt{k}\)
Et on peut généraliser cet agencement des carpettes à toutes les racines carrées des nombres entiers strictement supérieurs à \(4\) qui ne sont pas des carrés parfaits.
Soit \(k\) un tel nombre, on a
\[n<\sqrt{k}<n+1\label{farcy_equa_7}\]
avec \(n\) un entier supérieur à \(2\).
On en déduit les deux encadrements :
d’une part par passage à l’inverse
\[\frac{k}{n+1}<\sqrt{k}<\frac{k}{n}\label{farcy_equa_8}\]
et d’autre part \(n^2<k<(n+1)^2\) c’est-à-dire
\[1\leqslant k-n^2\leqslant 2n.\label{farcy_equa_9}\]
On raisonne à nouveau par l’absurde.
Il existe donc un couple d’entiers \((a,b)\in(\mathbb{N}^{\ast})^2\) tels que \(\sqrt{k}=\dfrac{a}{b}\) et \(a\wedge b=1\).
\(a\) et \(b\) sont donc les plus petits entiers possibles.
On a \(a^2=kb^2\) et on construit la première carpette en plaçant \(n^2\) carrés de côté \(b\) dans le carré de coté \(a\). C’est possible sans recouvrement puisque d’après (7) \(bn< a\) et on peut donc les espacer régulièrement avec des bandes non couvertes de longueur \(a\) et de largeur \(\dfrac{a-nb}{n-1}\) puisque \(n\geqslant2\).
On va maintenant construire la seconde carpette (en vert) en recouvrant \(k-n^2\) carrés de côté \(b\). C’est possible puisque \(n\geqslant 2\) et avec (9) :
\(1\leqslant k-n^2\leqslant 2n\leqslant n^2\).
L’aire de recouvrement est l’aire des \((k-n^2)\) carrés de côté \(b\) :
\(\mathscr{A}_{\text{r}}=b^2(k-n^2).\)
Pour l’aire non couverte, on additionne l’aire des \((n-1)\) rectangles horizontaux de longueur \(a\) et l’aire des \(n(n-1)\) rectangles verticaux de longueur \(b\).
\[\begin{aligned}
\mathscr{A}_{\text{nc}}&=(n-1)a\frac{a-nb}{n-1}+n(n-1)b\frac{a-nb}{n-1}\\
&=a(a-nb)+nb(a-nb).\end{aligned}\]
On applique maintenant notre théorème des carpettes :
\(b^2(k-n^2)=a(a-nb)+nb(a-nb)\)
soit \(b(kb-na)=a(a-nb)\) ; on a donc \(\dfrac{a}{b}=\dfrac{kb-na}{a-nb}\) avec \(0<kb-na<a\) d’après (8) et \(0< a-nb< b\) d’après (7) d’où la contradiction.
Pour \(\sqrt{3}\) et \(\sqrt{5}\), Steven J. Miller et David Montague proposent d’autres démonstrations s’inspirant de l’article de J. Conway à l’aide de triangles et de pentagones [3], chemin suivi plus récemment par Ricardo A. Podestá [4] mais sans généraliser.
Références
-
[1] Titu Andreescu et Bogdan Enescu. Mathematical Olympiad Treasures. Birkhäuser, 2004.↩
-
[2] J. Conway. The power of mathematics.
.↩
-
[3] Steven J. Miller et David Montague. Irrationality from the book.
. 2018.↩
-
[4] Ricardo A. Podestá. A geometric proof that \(\sqrt{3}\), \(\sqrt{5}\) et \(\sqrt{7}\) are irrational. v. 2020.
↩
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Yves Farcy, professeur de mathématiques au collège de la Vallée du Thoré à Labastide-Rouairoux, membre du groupe Jeux Mathématiques de l’IRES de Toulouse, est l’actuel président de la Régionale de Toulouse de l’APMEP.