Quand l’analyse cherchait ses mots

Si les mots géométrie, algèbre, arithmétique ou probabilités sont relativement bien compris dans la société, il n’en est pas de même pour le mot analyse. Pierre Legrand nous expose l’évolution, au fil des siècles, de ce terme en mathématiques.

« De toutes les grandes conceptions qui honorent l’esprit humain,
l’analyse infinitésimale est peut-être la plus remarquable ».
Charles Bossut, Histoire des mathématiques (1810)

Pierre Legrand

© APMEP Décembre 2021

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Nul, de nos jours, ne s’étonne d’entendre un ministre annoncer une mesure prise « en fonction de l’évolution des variables économiques » : chacun comprend aussitôt qu’il va falloir se serrer la ceinture. Nul ne s’étonne non plus de voir un journal évoquer « la croissance exponentielle de la population » de tel pays africain, ou de lire qu’un patron de choc entend « maximiser le ratio chiffre d’affaires/masse salariale ». On serait tenté d’en conclure que les concepts de l’analyse mathématique ont miraculeusement pénétré la France de nos élites. Mais faut-il vraiment le croire ?

Parlez à un non-scientifique de géométrie, d’algèbre, d’arithmétique ou de probabilités : il saura vaguement de quoi il s’agit. Prononcez devant lui le mot analyse : il pensera au laboratoire qui teste son cholestérol, au psycho-divan sur lequel il étale ses complexes ou, s’il est porté sur les choses de l’esprit, au tandem analyse-synthèse cher à son professeur de philosophie ; il est peu probable, en revanche, qu’il pense aux mathématiques.

Un tel paradoxe vaut d’être analysé.

Deux millénaires de mathématiques sans analyse ?

Le mot analyse vient de la Grèce antique. Aristote oppose αναλυσις (ana : en remontant ; lysis : décomposition) et συνθεσις (syn : avec ; thesis : action de poser) comme l’ont fait à sa suite tous les philosophes.

Le terme est dès le début du XVII^e siècle passé dans la langue française. Le dictionnaire de Furetière (1690), qui fit longtemps autorité, le définit comme « examen de quelque discours ou proposition, en recherchant ses principes, sa construction », mais n’évoque aucunement un sens mathématique. Le mot figure pourtant dans son contemporain le Dictionnaire mathématique d’Ozanam (1691), premier du genre¹, mais avec une bien curieuse définition, qui l’apparente à la fois à l’induction et au raisonnement par l’absurde.

Ce dictionnaire d’Ozanam est un intéressant témoignage de la situation à la fin du XVII^e siècle. Il se termine par une énorme « Table alphabétique des termes expliquez² dans ce livre », qui comporte quelque six-mille rubriques. Il y a par exemple quatre-vingt-trois entrées correspondant au mot nombre assorti d’une variété de qualificatifs. Mais le mot fonction est absent, tout comme des termes aussi familiers à nos lycéens que constant(e), croissant(e), décroissant(e), dérivée, intégrale, limite³, maximum, minimum, série, suite, variable.

Il serait léger d’en conclure qu’au XVII^e siècle l’analyse mathématique n’existait pas encore. Ce serait faire bon marché d’une pléiade de savants illustres, de Cavalieri à Barrow en passant par Descartes, Fermat, Pascal et bien d’autres… sans oublier le grand précurseur, Archimède. Ils ont résolu au coup par coup quantité de problèmes relevant de l’analyse ; mais la plupart du temps ce n’était pour eux qu’un outil pour traiter une question de géométrie, de mécanique ou d’optique. Comme monsieur Jourdain faisait de la prose sans le savoir, ils faisaient de la théorie des fonctions sans le savoir.

Les pères fondateurs : Leibniz et Newton

Ce n’est qu’à l’extrême fin du XVII^e siècle que Newton et Leibniz, chacun de leur côté, fondèrent l’analyse mathématique au sens où nous l’entendons. Mais aucun des deux n’employait ce terme. Newton parlait de method of fluxions, Leibniz de calculus differentialis. Il est assez plaisant, d’ailleurs, de constater que les Anglais, qui à l’époque traînaient Leibniz dans la boue en l’accusant de plagiat, ont finalement adopté le terme calculus là où maintenant les continentaux parlent d’analyse.

Le « calculus » de Leibniz

La terminologie de Newton étant restée sans lendemain, c’est celle de Leibniz qui est à l’origine de la nôtre. Elle a été ébauchée dans deux articles des Acta eruditorum, rédigés en latin. Dans le premier (Nova Methodus pro Maximis et Minimis, 1684), Leibniz introduit la différentielle, considérée comme un accroissement instantané (en un sens non précisé). Il l’appelle differentia et, comme nous, la note \(\mathrm{d}x\) ou \(\mathrm{d}y\). Le second article (De Geometria Recondita⁴ et Analysi indivisibilium atque infinitorum, 1686) introduit l’intégration comme opération inverse de la différentiation et la note par le symbole \(\displaystyle\int\). Dans l’un et l’autre texte, les démonstrations sont absentes ou remplacées par de simples analogies, comme dans l’extrait ci-dessous :

[…] méthodo tangentium exposui, patet esse \(\mathrm{d}\dfrac{{1}}{{2}}xx=x\,\mathrm{d}x\) ; ergo contra \(\dfrac{{1}}{{2}\mathstrut}xx=\displaystyle\int x\,\mathrm{d}x\) (ve enim potestates & ; radices in vulgaribus calculis, sic nobis summae et differentiae seu \(\displaystyle\int\) et \(\mathrm{d}\), reciprocae sunt). Habemus ergo …

[…] j’ai exposé par la méthode des tangentes, il est évident que \(\mathrm{d}\left(\dfrac{{1}}{{2}}xx\right)=x\,\mathrm{d}x\) ; donc inversement \(\dfrac{{1}}{{2}}xx=\displaystyle\int x\,\mathrm{d}x\) (car, comme les puissances et les radicaux dans le calcul ordinaire, ainsi pour nous somme et différence, autrement dit \(\displaystyle\int\) et \(\mathrm{d}\), sont réciproques). Nous avons donc…

L’« Analyse des infiniment petits »

Le terme « analyse », entendu dans un sens proprement mathématique, est pour la première fois apparu au grand jour en 1696, avec l’Analyse des infiniment petits pour l’intelligence des lignes courbes de Guillaume de l’Hôpital⁵. Le livre, qui eut un large succès, voulait mettre à la portée d’un public plus étendu que le petit cercle des chercheurs les principes du calcul différentiel de Leibniz.

Le titre même de l’ouvrage montre que l’analyse n’y est pas considérée comme une discipline indépendante, mais comme un instrument au service de la géométrie. Guillaume de l’Hôpital y considère une courbe comme « l’assemblage d’une infinité de lignes droites [nous dirions maintenant : segments], chacune infiniment petite ». Le point de vue est donc bien celui d’un raisonnement par décomposition et justifie l’usage par l’auteur du mot « analyse », qu’il n’emploie d’ailleurs jamais isolément mais muni d’un qualificatif : « analyse des infiniment petits » et non « analyse » tout court.

Vers l’« analyse » tout court

Un pas supplémentaire fut franchi par l’Encyclopédie de Diderot et d’Alembert, publiée de 1751 à 1772 :

Il n’empêche que les deux cours d’analyse les plus répandus du XVIII^e siècle finissant, publiés l’un et l’autre en 1797, ne font pas référence à ce terme. Celui de Lagrange s’intitule Leçons sur le calcul des fonctions, celui de Lacroix Traité du calcul différentiel et du calcul intégral.

Il fallut attendre Cauchy et son Cours d’Analyse de l’École royale polytechnique (1821), pour voir entrer définitivement le sens moderne du mot analyse dans le vocabulaire mathématique courant.

Les dictionnaires de langue mirent du temps à l’accepter. Dans le Littré de 1873, on lit ceci :

Un siècle plus tard, l’article « analyse » du Grand Larousse encyclopédique de 1967 marque même une régression par rapport au Littré… et un retour au point de vue d’Ozanam :

Manière de résoudre les problèmes en supposant connues les quantités que l’on cherche, pour développer ensuite les conséquences de cette hypothèse […]

Heureusement, l’actuel Petit Robert sauve l’honneur des lexicographes et parle d’étude de fonctions.

Les débuts du vocabulaire des fonctions

Pendant les décennies qui ont suivi sa naissance, le nouveau calcul a cruellement manqué d’un langage précis qui lui soit propre.

L’ouvrage Analyse des infiniment petits de Guillaume de l’Hôpital, déjà cité, est un bon point de repère. Si l’on voit apparaître dans la préface les expressions « calcul différentiel » et, bien que l’auteur n’en traite pas, « calcul intégral », les termes « fonction », « variation », « limite » sont absents du livre, même dans la seconde édition datée de 1716.

En revanche le mot « variable » se retrouve plusieurs fois, soit comme adjectif accolé à « quantité » soit indépendamment : « les données & variables ». Il lui arrive cependant de mettre « inconnue » là où nous mettrions « variable », comme ici : « faire évanouir⁶ les inconnues ». Et il ne parle jamais de « constantes », mais de « données ». Comme Leibniz, il écrit « différence » pour « différentielle ».

Il fallut attendre le milieu du XVIII^e siècle pour voir apparaître dans un traité de mathématiques le mot « fonction ». Il s’agissait d’un gros ouvrage d’Euler, Introductio in analysin infinitorum (Introduction à l’analyse des infinis), publié en 1748.

Dans le chapitre 1 (dont l’en-tête est reproduit ci-dessus) sont définis pour la première fois les termes « fonction » et « constante » :

Functio quantitatis variabilis est expressio analytica quomodocumque composita ex illa quantitate variabili et numeris seu quantitatibus constantibus.⁷

Euler reprend aussi une convention de Descartes dont nous avons hérité : réserver les premières lettres de l’alphabet aux constantes, les dernières aux variables (si ce n’est que pour Descartes il s’agissait de distinguer les données des inconnues).

C’est à Euler encore que nous devons la première apparition de \(f({\dots})\) pour désigner une fonction, dans un article⁸ de 1734 : « si \(f\left(\dfrac{x}{a}+c\right)\) désigne une fonction quelconque de ce même \(\dfrac{x}{a}+c\) … ». L’idée était dans l’air : à la même époque, Clairaut écrivait une fonction de \(x\) sous la forme \(\Phi x\) ou \(\Pi x\), sans utiliser de parenthèses.

Cette notation qui nous est devenue familière mit quelque temps à s’imposer. Lagrange, en 1806 dans ses Leçons sur la théorie des fonctions, écrit bien \(f(x+a)\), mais il abrège systématiquement \(f(x)\) en \(fx\). Il fallut attendre Cauchy et son Cours d’analyse de l’École polytechnique (1821) pour régler définitivement la question (encadré ci-dessous).

Trois arrivées tardives

La dérivée

Les mathématiciens du XVIII^e siècle ont abondamment utilisé les différentielles mais, curieusement, sans jamais parler de dérivée. L’introduction de celle-ci est due à Lagrange, avec déjà la notation \(f’\), mais avec une définition plus restrictive que la nôtre. Dans son ouvrage Leçons sur la théorie des fonctions (1806) déjà cité⁹, il présente en effet les dérivées successives en un point \(x\) comme coefficients du développement en série entière au voisinage de ce point (je respecte ses notations) : \[f(x+i)=fx+if’x+\frac{i^2}{2}f’\!’x+\frac{i^3}{2.3}f’\!’\!’x+\cdots\]

Le problème, évidemment, est que toute fonction dérivable (au sens moderne) n’est pas ainsi développable¹⁰, ce qu’on lui fit assez vite observer.

La notation \(\displaystyle\sum\)

Jusqu’au début du XIX^e siècle, aucune notation spécifique n’existait pour désigner une somme infinie ou de longueur arbitraire. C’est ainsi que, dans son Introductio in analysin infinitorum de 1748, qui donne une place importante aux séries entières, Euler écrit celles-ci sous la forme \(A+Bz+Cz^2+Dz^3+\&c\).

Ce fut pourtant Euler qui, quelques années plus tard, en 1755, introduisit le symbole \(\displaystyle\sum\) : « summam indicabimus signo \(\displaystyle\sum\) »¹¹. Il le fit en passant, sans insister, et il fallut près d’un siècle pour que cette nouveauté pourtant bien commode passe dans l’usage courant. Le Cours d’analyse de Cauchy (1820), par exemple, ne l’utilise pas. Mais, en 1841, Weierstrass écrit déjà des choses comme \(F(x)=\displaystyle\sum_{\nu=-\infty}^{\nu=+\infty}A_{\nu}x^{\nu}\).

La notation \(u_n\)

On vient de voir ci-dessus Weierstrass utiliser la notation indicielle \(A_{\nu}\). L’indexation des termes d’une suite (écriture \(u_n\)) semble postérieure à 1770. La référence la plus ancienne que je connaisse figure dans un mémoire de Lagrange, Recherche sur les suites récurrentes, daté de 1775 (cf. encadré ci-dessous¹²).

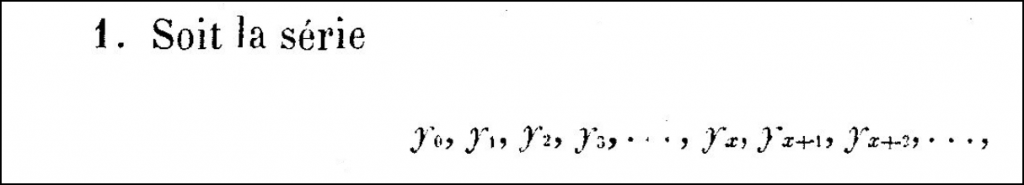
Un enrichissement progressif

Au fil des XIX^e et XX^e siècles, il y eut enrichissement et uniformisation progressifs d’un langage de plus en plus proche de celui qu’utilisent nos classes et nos universités. Donnons quelques jalons.

En 1822, Fourier introduisit la notation \(\displaystyle\int_{a}^{b}\) qui fut très vite adoptée. En revanche, l’écriture des limites mit longtemps à se fixer. Si, dès 1786, Simon Lhuilier utilisait déjà dans son Exposition élémentaire des principes des calculs supérieurs la notation « \(\lim\) », celle-ci a connu divers avatars au cours du XIX^e siècle. La forme la plus courante à l’époque, « \(\lim\limits_{x=a}f(x)\) » n’a cédé la place au « \(\lim\limits_{x\to a}f(x)\) » qui nous est familier qu’au début des années 1900. Et les notations de Landau \(f=o(g)\) et \(f=O(g)\) datent des années 1920.

L’idée d’attribuer un nom aux principaux ensembles de nombres est, elle aussi, tardive. Le plus ancien est \(\mathbb{N}\), qui apparut en 1888 dans un écrit de Dedekind, Was sind und was sollen die Zahlen ?¹³ et fut repris en 1889 dans les fameux Arithmetices Principia de Peano (mais tous deux appelaient \(\mathbb{N}\) ce que nous appelons \(\mathbb{N}^{\ast}\)). Détail pittoresque : pour le premier, \(\mathbb{N}\) signifiait Nummer (numéro en allemand), mais pour le second, \(\mathbb{N}\) signifiait Numerus (nombre en latin).

Les notations \(\mathbb{Z}\), \(\mathbb{Q}\), \(\mathbb{R}\) et \(\mathbb{C}\) semblent dater de la période 1930-1950, car elles figurent déjà à cette époque dans les Éléments de mathématique de Bourbaki, qui ont joué un rôle important dans la normalisation des écritures (ils ont par exemple systématisé l’usage des « crochets expressifs » \([{\dots}]\), \(]{\dots}[\), \(]{\dots}]\) et \([{\dots}[\)). Plus précisément, les écritures \(\mathbb{Z}\), pour Zahl, (nombre en allemand) et \(\mathbb{Q}\) pour Quotient émanent très vraisemblablement du traité de Bourbaki, mais son antériorité est moins sûre pour \(\mathbb{R}\) et \(\mathbb{C}\). Notons enfin qu’il écrivait ces symboles en caractères gras sans la double barre, apparue plus tard.

La situation actuelle

De nos jours, la diffusion mondiale de l’enseignement des mathématiques et l’usage majoritaire de l’anglais dans les publications scientifiques ont conduit à une standardisation poussée. Si chaque langue garde sa terminologie mathématique propre, on peut passer de l’une à l’autre sans ambiguïté : ainsi série entière se dit power series en anglais et Potenzreihe en allemand, mais ces termes recouvrent exactement la même notion. Et surtout équations et formules (écrites de gauche à droite en caractères latins et à l’occasion grecs) sont à peu près totalement internationalisées.

Pour un Européen de l’Ouest ou un Américain, il s’agit là d’une situation fort agréable. Pour un Européen de l’Est habitué aux caractères cyrilliques, c’est déjà un peu moins plaisant.

Pour un Chinois ou un Japonais, formé à une écriture idéographique disposée de haut en bas, cela représente une laborieuse gymnastique ; mais un étudiant qui a dû mémoriser quelques milliers de caractères n’a sans doute pas grand mal à avaler une ou deux centaines de symboles supplémentaires et une disposition différente !

À titre de curiosité, vous pouvez voir ci-contre un extrait de l’examen d’entrée dans les universités publiques japonaises en 2019.

Le principal îlot de résistance se situe dans les pays arabes, dont la langue s’écrit de droite à gauche avec des lettres liées (en omettant la plupart du temps les voyelles), ce qui ne facilite évidemment pas les choses. Leur enseignement supérieur s’est adapté bon gré mal gré aux normes internationales, mais la situation est beaucoup moins nette dans l’enseignement secondaire, où l’usage mathématique se heurte à l’usage courant. On peut le regretter, mais n’oublions pas, avant de critiquer, que la nation qui, à tort ou à raison, s’estime la plus évoluée de toutes, les États-Unis, persiste à rechigner devant le système métrique¹⁴… et impose de fait au reste du monde de mesurer en pouces les diagonales des écrans et en pieds les altitudes des avions.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Pierre Legrand a depuis longtemps un rôle actif au sein de l’APMEP. Il a écrit de nombreux articles dans le bulletin de l’association.