Inclusion mixte et résolution de problèmes

Comment permettre à tous les élèves de l’école élémentaire de résoudre des problèmes ? C’est la question que se sont posée Anne Davesne, Isabelle Ménard et Florence Peteers. Elles nous présentent ici deux exemples d’inclusion mixte, mêlant étayage d’un enseignant spécialisé et co-enseignement avec l’enseignant de référence.

Anne Davesne, Isabelle Ménard & Florence Peteers

© APMEP Septembre 2022

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

L’inclusion des élèves à besoins éducatifs particuliers (BEP) constitue actuellement un véritable défi pour l’école. Plusieurs lois ont permis des avancées majeures en matière de scolarisation de ces élèves. En effet, la scolarisation par l’Éducation nationale de tous les enfants en situation de handicap en milieu ordinaire a été rendue obligatoire par la loi du 11 février 2005 pour l’égalité des droits et des chances, la participation et la citoyenneté des personnes handicapées. La loi du 8 juillet 2013 d’orientation et de programmation pour la refondation de l’École de la république a ensuite posé les fondements de l’école inclusive en ces termes : «Le service public reconnaît que tous les enfants partagent la capacité d’apprendre et de progresser. Il veille à l’inclusion scolaire de tous les enfants, sans distinction». Avec cette loi, on observe un changement de paradigme : ce n’est plus à l’élève en situation de handicap de s’adapter au contexte scolaire, mais à l’école d’aménager pour lui les situations d’apprentissage afin de le faire progresser. L’objectif est d’aller vers une école toujours plus inclusive sachant s’adapter aux besoins spécifiques. Dernièrement, la loi du 26 juillet 2019 pour une école de la confiance présente une série de mesures visant à renforcer l’école inclusive.

Dans la mise en place de cette école inclusive, l’enseignant spécialisé joue un rôle crucial en tant qu’expert de l’analyse des élèves à BEP et des réponses à construire et, également, par sa fonction de personne ressource (diffusion des enjeux éthiques et sociétaux de l’école inclusive, animation d’actions de sensibilisation, mise en œuvre de modalités de co-intervention…).

Difficultés observées

Le passage à une école inclusive est source de nombreuses difficultés professionnelles que ce soit du côté de l’enseignant ordinaire ou du côté de l’enseignant spécialisé. En effet, la présence d’élèves en situation de handicap dans la classe peut susciter l’inquiétude des enseignants, en particulier en cas de troubles cognitifs ou de troubles du comportement. Face à une hétérogénéité de plus en plus grande nécessitant une modification des pratiques (réflexion sur l’accessibilité des tâches et différenciation des apprentissages), certains enseignants peuvent se sentir démunis. Les enseignants spécialisés sont ainsi confrontés à la résistance de certains de leurs collègues à inclure leurs élèves dans des classes déjà bien difficiles à tenir.

Le co-enseignement est également source de difficultés. Nous en pointons deux :

• il demande de la part de l’enseignant de la classe de référence d’ouvrir celle-ci à l’enseignant spécialisé ;

• il nécessite une forte collaboration entre les enseignants impliqués. Or, ceux-ci ne bénéficient pas toujours d’espace dédié ni de temps alloué pour développer collectivement leurs séances.

Difficultés des élèves dans la résolution de problèmes

La résolution de problèmes joue un rôle essentiel dans l’activité mathématique et occupe une place centrale dans les programmes de l’école primaire. On peut en effet lire dans les programmes du cycle 2 que «la résolution de problèmes est au centre de l’activité mathématique des élèves, développant leurs capacités à chercher, raisonner et communiquer». Il s’agit cependant d’une activité complexe qui nécessite la coordination de plusieurs compétences [1], source de nombreuses difficultés chez les élèves et en particulier des élèves à BEP.

Les recherches [2] semblent montrer que les aides méthodologiques sont insuffisantes mais que c’est en résolvant des problèmes dans leur globalité qu’on apprend à les résoudre. Or, les élèves en difficulté rencontrent peu d’occasion de mener à terme le processus de résolution en classe, ce qui ne fait qu’accentuer leurs difficultés.

Expérience d’Anne : inclusion soutenue par le RASED¹

Constats des difficultés des élèves lors de la résolution de problèmes

En 2020-2021, je suis intervenue auprès d’un groupe de quatre élèves de CE2 en grande difficulté en mathématiques, dans le cadre du dispositif RASED.

Lors de la résolution de problèmes arithmétiques, l’enseignante constatait régulièrement que les élèves les plus fragiles de la classe avaient tendance à faire un calcul, bien souvent une addition avec les nombres qu’ils voyaient dans l’énoncé. Elle a donc souhaité comprendre pourquoi ils ne mettaient pas en place une réflexion, comment ils pouvaient se satisfaire de réponses bien souvent très en décalage avec la situation proposée et surtout comment mener des séances de résolution de problèmes qui permettraient à tous les élèves de réfléchir afin de résoudre le problème proposé.

Lors d’un temps d’échange entre l’enseignante de la classe, les membres du RASED et le directeur, l’enseignante avait exposé les difficultés de certains élèves. J’ai donc décidé de les évaluer individuellement afin de repérer précisément les points d’appui et les difficultés de chacun. J’ai constaté la difficulté qu’ils avaient à se représenter la situation et à mettre en œuvre une stratégie adaptée dans un but de résolution.

Nous avons donc convenu avec l’enseignante de CE2 de mettre en place une séquence dans laquelle les élèves auraient pour objectif de schématiser et d’expliciter leurs choix. Les dessins des élèves devaient nous permettre de comprendre ce qu’ils avaient compris de la situation et de mieux appréhender leurs stratégies de résolution et leurs erreurs. Les schémas devaient également mettre en évidence le fait que la résolution de problèmes ne se construit pas sur une procédure liée au hasard.

Il nous a semblé que les objectifs ciblés pourraient servir à tous les élèves et aider l’enseignante à travailler autrement la résolution de problèmes, en mettant l’accent sur le sens plus que sur le résultat et en aidant les élèves à prendre conscience de leurs stratégies. Nous avons alors convenu de mettre en place un dispositif de type anticipation / séance en classe en co-enseignement, se basant sur les recherches de Marie Toullec-Théry [3]. L’objectif d’un tel dispositif est de permettre de lever les obstacles didactiques afin que les élèves à BEP puissent participer efficacement à la séance de résolution de problèmes en classe. J’ai donc préparé et mené une séance en RA (Regroupement d’Anticipation) le mardi après-midi avec les quatre élèves à BEP afin de travailler les notions nécessaires à la future séance de résolution de problèmes. J’ai fait un bref retour à l’enseignante de CE2 avant la séance en classe qui a eu lieu le vendredi matin suivant et à laquelle tous les élèves ont participé.

Choix des énoncés et progression

Il a ensuite fallu choisir les énoncés de sorte que la difficulté soit croissante. Nous pouvions jouer sur les données numériques, la présence d’éléments inutiles, la présence d’étapes intermédiaires… Ces variables étaient certes intéressantes mais non suffisantes. Afin de construire cette progression, je me suis appuyée sur la typologie des problèmes de Vergnaud [4] en ne gardant que les problèmes additifs et soustractifs.

Nous avons donc construit, en gardant cette typologie, la progression suivante qui correspond à nos objectifs de schématisation et d’explicitation.

• Transformation positive avec recherche de l’état final.

  Lucas possède une collection de \(45\) figurines de super-héros. Son frère lui en donne \(18\) nouvelles. Combien de figurines Lucas possède-t-il maintenant ?

• Transformation négative avec recherche de l’état final.

  Pour l’anniversaire de sa fille, la maman de Léa a acheté \(48\) sucettes qu’elle a mises dans un pot. Les invités ont gagné \(33\) sucettes au cours des différents jeux. Combien de sucettes reste-t-il dans le pot à la fin de l’anniversaire ?

• Transformation positive avec recherche de la transformation.

  À la fin de la première mi-temps, l’équipe A de basket affiche un score de \(38\) points. À la fin du match, le tableau des scores affiche pour eux \(50\) points. Combien ont-ils marqué de points pendant la deuxième mi-temps ?

• Transformation négative avec recherche de la transformation.

  Les parents de Manel vont faire les courses avec \(55\) €. En rentrant, ils ont \(17\) € dans leur porte-monnaie. Combien d’argent ont-ils dépensé ?

• Transformation positive avec recherche de l’état initial.

  Lucas possède une collection de figurines de super-héros. Son frère lui en donne \(18\) nouvelles. Il en possède maintenant \(43\). Combien de figurines Théo possédait-il avant d’obtenir celles de son frère ?

Les typologies étant sélectionnées, nous pouvions agir sur les variables didactiques. Afin de réellement proposer une séance en anticipation, nous avons décidé de garder les mêmes énoncés entre le temps en regroupement et le temps en co-enseignement. Lors du temps en RA, les élèves pourraient s’aider de matériel afin de proposer une première représentation de la situation. Ce temps de manipulation devrait permettre aux élèves d’accéder à la schématisation. Afin que la manipulation soit possible, les élèves travailleraient sur des données numériques différentes de celles qu’ils retrouveraient en classe le vendredi suivant. L’idée était également de développer les compétences métacognitives (souvent déficitaires chez les élèves à BEP) et permettre aux élèves de transférer les compétences travaillées en RA en classe. Le choix d’un habillage similaire avec des données numériques différentes pouvait permettre de travailler ce transfert.

Déroulement des séances

Afin de développer la pensée réflexive des élèves, nous avons décidé de construire les séances de co-enseignement sur le modèle des séances d’aide avec trois temps bien distincts. Pour que les séances puissent répondre aux besoins de l’enseignante, nous avons convenu de nous partager les temps de la séance.

L’enseignante de la classe a mené le temps 1 durant lequel les élèves ont rappelé ce qu’ils avaient fait et appris lors de la séance précédente. Elle a progressivement pris en main le rappel des stratégies mises en avant et le fait de co-enseigner lui a permis de prendre de plus en plus de place dans les séances. Le temps 2 a été le temps pendant lequel les élèves étaient en phase de recherche, mais surtout le temps pendant lequel nous leur avons imposé un moment de mise en évocation : je leur ai lu l’énoncé et leur ai demandé de fermer les yeux pour se faire «le film de l’énoncé», «les images mentales». Je suis ensuite revenue vers eux en faisant deux mises en évocation : la première portait sur les circonstances, les lieux, les personnages et la seconde se focalisait sur la question posée et sur ce qu’ils «voyaient d’important dans leur film pour y répondre».

Ainsi, dans le problème de l’anniversaire de Léa, les élèves ont imaginé le décor, les ballons, les bonbons…

À la suite de la seconde mise en évocation, les élèves n’ont «regardé» que le bocal de bonbons afin de comprendre ce qui s’y passait, à savoir que le bocal se vidait progressivement. Ils ont donc utilisé la question pour focaliser leur attention sur les éléments importants. Je leur ai ensuite demandé de réfléchir à ce qu’ils allaient faire en premier, et ensuite…

Puis, afin de développer l’auto-contrôle là encore déficitaire chez les élèves à BEP, je leur ai demandé de nommer des aides possibles à la résolution telles que les affichages présents en classe, un cahier de références mathématiques, les affiches des stratégies évoquées au fur et à mesure des séances, ou la maîtresse.

Une fois ce travail préalable de réflexion mené, les élèves sont entrés dans la tâche. Mon regard s’est principalement porté sur les élèves à BEP en me demandant :

• Sont-ils en mesure de réinvestir le travail fait en RA ?

• Comment les aider à démarrer ?

• Quel soutien à la mémorisation leur offrir ?

L’enseignante est passée voir les élèves, notant sur un carnet les points de blocage afin de les lever lors de la mise en commun. Lorsque les blocages étaient communs à plusieurs élèves, nous avons proposé un temps de pause réflexive pour rappeler aux élèves ce qu’ils cherchaient, les aides à disposition, ce qu’ils envisageaient de faire d’abord, puis ensuite… mais aussi les critères de réussite ou encore l’objectif de la séance.

Est ensuite venu le temps de mise en commun au cours duquel les élèves sélectionnés par l’enseignante (pour les difficultés qui avaient émergé, pour une stratégie particulièrement intéressante, un schéma à expliciter, …) sont venus au tableau pour montrer leur travail de recherche et l’expliquer à leurs camarades.

De là ont émergé les stratégies importantes que j’ai notées au tableau. L’enseignante a ensuite fait un retour sur l’objectif et nous avons énoncé l’objectif de la séance suivante. Les objectifs ont évolué car ils étaient principalement centrés sur le schéma (faire un dessin rapide, ne pas dessiner de détails, ne pas utiliser les crayons de couleur) et ont évolué vers une résolution plus experte (utiliser la question pour «ne regarder que les éléments importants», montrer par une flèche ou un symbole l’action de supprimer ou ajouter, traduire son schéma en calcul et expliquer le choix du calcul).

Au cours de la séance, je n’étais pas figée auprès des élèves à BEP car nous avions décidé de circuler dans la classe afin de favoriser les échanges, pour sélectionner les élèves à faire venir au tableau, proposer l’objectif de la séance suivante…

Au cours de la mise en commun, la parole a été donnée à tous les élèves y compris aux élèves à BEP qui avaient accepté d’expliquer ce qu’ils avaient fait et souhaitaient montrer leur recherche au reste de la classe.

Apports

Les élèves à BEP, devant le même problème que le reste de la classe, ont pu participer sans être stigmatisés dans un coin.

Le bilan a donc été positif pour ces élèves et pour l’enseignante qui a évolué dans la manière de mener les séances. Nous n’avons pas pu poursuivre les séances à cause du confinement mais la collègue a souhaité reprendre la séquence en co-enseignement en mettant en place des ateliers.

Concernant les mathématiques, les élèves ont appris que «plaquer» un calcul (et bien souvent une addition) en réponse à une question ne permettait pas de trouver la bonne réponse. Ils ont compris que résoudre un problème nécessite de prendre le temps de rechercher le sens de l’énoncé et une stratégie de résolution la plus efficace. Les élèves ont ainsi mis du sens sur les nombres donnés dans l’énoncé. Les séances ont également permis de construire collectivement une démarche de résolution, et ont déconstruit l’idée selon laquelle résoudre un problème correspond à faire un calcul.

Expérience d’Isabelle : inclusion soutenue par l’ULIS²

Constats des difficultés des élèves lors de la résolution de problèmes

En tant que coordonnatrice ULIS³, j’ai pu travailler avec des collègues en co-enseignement lorsque les élèves du dispositif étaient en classe ordinaire. J’ai remarqué qu’en classe, la difficulté première de mes élèves de CE2 était d’élaborer et de se souvenir des différentes stratégies permettant de résoudre des problèmes. Il a donc fallu permettre aux élèves de mettre en place des procédures personnelles et d’en prendre conscience. Il était important aussi de viser la construction d’outils leur permettant d’être autonomes face à la tâche mathématique. Les situations problèmes en étaient un exemple. Avec mes collègues, nous avons réfléchi à la question suivante : comment permettre à tous les élèves de la classe de participer au rallye mathématique du département ?

Choix des énoncés et progression

Dans un premier temps ma démarche a été d’évacuer toutes les difficultés liées au système de numération (opérations, utilisations des nombres) des élèves inclus dans le dispositif. J’ai donc opté pour des problèmes ouverts (tâches complexes sans nombre). Ce type de tâche permet la mise en œuvre de diverses stratégies de résolution : il y a donc plusieurs entrées favorisant ainsi l’accessibilité pédagogique. En amont, la collègue de classe ordinaire et moi-même avons regardé les problèmes posés aux différents rallyes mathématiques de l’année précédente et avons choisi dans une banque de problèmes ceux qui répondaient aux critères demandés : trier des informations, comparer, modéliser et raisonner pour résoudre ce type de problème.

Déroulement des séances

Chaque semaine nous avons sélectionné trois problèmes : les deux plus simples étaient travaillés par anticipation au sein du dispositif ULIS et le dernier, au sein de la classe de référence, à l’occasion d’un temps de co-enseignement. Pour les trois problèmes, la démarche à mobiliser était la même mais c’est la difficulté qui évoluait progressivement (figure 1).

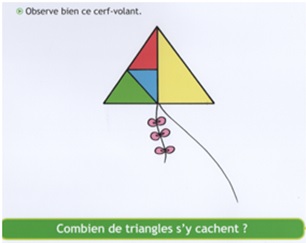		Observe bien ce damier Combien de carrés s’y cachent ?
Problèmes proposés en anticipation		Problème proposé en co-enseignement

Figure 1. Exemple de progression autour d’un problème de dénombrement de figures géométriques.

Lors du travail par anticipation je visais la mise en place de stratégies chez les élèves et les questionnais pour qu’ils puissent en prendre conscience. L’objectif était qu’ils soient les plus autonomes possible dans leur classe de référence grâce à la mise en place d’un auto-contrôle.

J’ai proposé le problème le plus simple avec une lecture oralisée et une explication du vocabulaire si besoin. Les objectifs visés étaient l’analyse des connaissances, des attitudes et des capacités de chacun face à ce type de problème ainsi qu’une élaboration de stratégies. J’ai aidé les élèves à s’organiser dans la construction de leur pensée. Nous avons utilisé des phrases types : «j’essaie de me souvenir» ou «je regarde dans mon cahier si j’ai déjà fait un problème semblable», ou encore «puis je sors mon matériel».

Ensuite, lors du second temps d’anticipation, je leur ai lu le problème et les ai amenés à repérer les ressemblances et les différences avec celui réalisé la veille pour dégager une similarité de structure. Lors de la résolution du problème, je les ai questionnés sur leurs démarches et sur les outils utilisés. Nous avons enrichi le répertoire de stratégies et nous avons comparé les différentes façons de faire.

Pour l’exemple du dénombrement de figures (figure 1), les stratégies répertoriées ont été les suivantes :

• je peux colorier les formes ;

• je peux demander à la maîtresse plusieurs fois la feuille ;

• je peux découper les formes ;

• je peux demander à la maîtresse les gabarits.

Lors du co-enseignement, je suis intervenue en table d’appui [5] avec deux élèves du dispositif et trois élèves à BEP de la classe. Les élèves du dispositif avaient leur cahier d’aide contenant outils et stratégies utilisés. Lors de ce moment de différenciation, j’ai posé des questions aux élèves pour les amener à reformuler le problème et à indiquer ce qui était recherché. Ils ont démarré la phase de recherche et je suis passée les questionner en posant des questions ouvertes qui visaient à ce que les élèves expliquent, a posteriori, les différentes actions mises en œuvre dans la réalisation de la tâche («explique-moi ce que tu as fait, comment tu as fait») ou les raisons de leur action. Ce questionnement métacognitif est centré sur leur démarche.

J’ai remarqué que les élèves du dispositif transféraient les connaissances et les stratégies apprises au sein de l’ULIS vers la classe. Comme ils avaient à leur disposition les outils et les aide-mémoires de leurs acquis, je n’ai eu qu’à les lancer dans cette tâche plus complexe mais qui restait dans leur zone proximale de développement grâce au travail mené par anticipation. Pour les autres élèves du petit groupe, j’ai essayé de leur fournir le même étayage que pour les deux élèves du dispositif (questionnement métacognitif). Lors des premières séances, cela leur paraissait difficile car ils n’avaient pas l’habitude de ce questionnement : j’ai remarqué un décalage entre mes deux groupes. Mais au fur et à mesure des séances, les élèves à BEP se sont saisis des outils et de ce questionnement. Le groupe est alors devenu presque homogène. Nous avons aussi fabriqué un répertoire des outils et des stratégies vues (classeur dans lequel sont répertoriées les stratégies en fonction des problèmes) :

Les problèmes ont évolué au cours de l’année : des données chiffrées, des opérations sont apparues. L’organisation a été la même : travail par anticipation puis co-enseignement. Les résultats ont été identiques. J’ai remarqué que le questionnement métacognitif était toujours nécessaire, car ces élèves n’arrivaient pas à se poser seuls les questions qui leur permettaient de trouver la solution. Ce questionnement pour l’étayage de la tâche restait plus important pour les élèves du dispositif, autant pour les élèves porteurs de handicap que pour les élèves à BEP.

Apports

Ce co-enseignement a profité à tous les élèves de la classe de CE2 car l’étayage proposé aux élèves du dispositif a pu aussi être proposé aux autres élèves. Leur regard sur les élèves du dispositif ULIS et sur moi-même a changé. Ces derniers n’étaient plus des élèves porteurs de handicap dont j’étais l’enseignante qui s’en occupait, mais plutôt des élèves en difficulté, au même titre que d’autres au sein de la classe dont je pouvais également m’occuper.

D’un point de vue mathématique, le travail sur les problèmes ouverts développé ici a permis de mettre les élèves en situation de recherche et de mobiliser différents modes de raisonnement selon leurs capacités (essai-erreur, analogie, déduction…).

Pour conclure

Dans cet article, nous avons présenté deux mises en œuvre de co-enseignement en résolution de problèmes. Les adaptations proposées par les enseignantes spécialisées ont permis de rendre accessible la séquence à tous les élèves, en particulier ceux présentant des BEP. Dans les deux cas, un travail d’anticipation des obstacles a été réalisé avec les élèves soutenus par le dispositif. Ce travail par anticipation et sa nature, le co-enseignement avec la richesse des co-élaborations et de co-ajustements avec l’enseignante de la classe, représentent la pierre angulaire du travail de l’enseignant spécialisé. C’est grâce à cela que les élèves ont pu réaliser des transferts opérants et devenir des élèves apprenants en classe. Nous voyons bien le rôle important de l’accompagnement. C’est aussi le rôle de l’AESH (Accompagnants d’Élèves en Situation de Handicap) qui apprend au sein du dispositif, puis en classe ordinaire, à ces élèves à devenir autonomes face à ce type de tâche.

L’intérêt de ce type de travail ne se limite pas aux élèves à BEP. En effet, tous les élèves profitent des aides et questionnements apportés par l’enseignant spécialisé lors des temps de co-enseignement. Il y a également des bénéfices pour les enseignants qui sont amenés à se questionner sur leurs choix pédagogiques. Le fait de travailler à deux est considéré comme un véritable avantage et les enseignants semblent avoir moins d’appréhension à changer leurs habitudes et à tester de nouvelles choses.

Références

1. J.F. Bergeault. « Résolution de problèmes et difficulté en mathématiques ». In : Bulletin de l’APMEP n°499 (2012). , p. 306-308.↩︎

2. C. Houdement. « Résolution de problèmes arithmétiques à l’école ». In : Grand \(\mathbb{N}\) n°100 (2017). , p. 59-78. ↩︎

3. M. Toullec-Théry. « Ingénieries didactiques coopératives et coenseignement pour contribuer à une scolarisation inclusive ». In : Éducation et francophonie n°48(2) (2020). , p. 116-138.↩︎

4. G. Vergnaud. « Psychologie du développement cognitif et didactique des mathématiques, un exemple : les structures additives ». In : Petit x n°22 (1989). , p. 51-59.↩︎

5. C. Lommé. « La table d’appui, un dispositif à découvrir ». In : Au fil des maths n°529 (2018). .↩︎

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Anne Davesne est professeure des écoles en RASED.
Isabelle Ménard est professeure des écoles en ULIS.
Florence Peteers est enseignante-chercheuse au laboratoire de didactique André Revuz (LDAR ).
Elles enseignent toutes les trois dans l’académie de Versailles.