Le débat scientifique

Depuis longtemps, l’IREM de Grenoble mène un travail sur la mise en œuvre du débat scientifique en classe. Où l’on fait le pari de s’appuyer sur les mathématiques pour construire la pensée et donc, dans une certaine mesure, le citoyen.

Marc Legrand, Thomas Lecorre, Liouba Leroux & Anne Parreau

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Commençons avec Marc Legrand, à l’origine de ce débat scientifique en classe, qui nous donne les fondements philosophique et conjoncturel de cette modalité pédagogique :

Quand on s’entretient avec des adultes sur ce qu’ils ont compris et retenu de nos enseignements de mathématiques, beaucoup avouent que même lorsqu’ils sont arrivés à suivre facilement et à avoir de bonnes notes, la façon dont on a discuté en classe de la nature, de la pertinence et de la vérité de nos propriétés générales est restée totalement extérieure à leurs préoccupations de vie : pour la plupart cela semble n’avoir en rien modifié leur façon de penser le monde et d’affronter la complexité des situations, cela paraît ne leur avoir donné aucune méthode de raisonnement pour aborder seul ou avec autrui les contradictions de leur propre vie et de la vie en société. Cet écart entre le monde mathématique et le monde de la vraie vie provoque chez beaucoup d’élèves — comme cela a été le cas pour moi — un sentiment d’étrangeté, de divorce forcé entre deux ordres de vérités qui ne peuvent s’enrichir de leurs différences. Je vais découvrir en passant du côté professeur que cet écart ne peut se réduire, comme je l’imaginais, par la simple organisation de discussions autour de problèmes concrets. Certes, le débat spontané d’élèves en Sixième ou d’étudiants au premier cycle universitaire rend le cours plus vivant, mais malheureusement il ne joue pas du tout le rôle cognitif que je pensais naïvement pouvoir lui attribuer : celui d’initier nos interlocuteurs à un mode de pensée qui les aide à découvrir en quoi le caractère universel de nos convictions spontanées est bien souvent inadapté, abusif ou grossièrement faux ! En écoutant attentivement l’argumentation de mes élèves sans tendre à corriger tout de suite ce qui n’allait pas, j’ai peu à peu réalisé qu’au niveau du sens, ils utilisaient les connecteurs logiques usuels (donc, car, par suite ; si…, alors…) comme dans la vie courante, i.e. ces connecteurs avaient pour chacun d’eux une signification si personnelle, si conjoncturelle et si « élastique » que tout ce que les uns avançaient pouvait être remis en cause par les autres en exploitant « la même logique apparente » , et finalement pour clore le débat, le professeur (en l’occurrence moi) devait — contre son intention initiale — trancher en sortant « un lapin du chapeau » ! Pour dépasser l’obstacle épistémologique que représente la mise en place d’une même façon de discuter rationnellement du vrai et du faux dans un groupe, j’ai ainsi ressenti l’impérieux besoin que tous les élèves du groupe classe ou amphi disposent d’une logique commune qui soit opérationnelle, i.e. une logique qui bien que formelle demeure suffisamment à portée de main de tous pour que chacun puisse peu à peu en devenir le porte-parole, puisse ainsi faire sienne la façon très spéciale dont les mathématiciens manipulent le « Si…, alors… » pour se mettre d’accord quand ils ne s’entendent plus ! Pour construire ensemble cette logique commune nous avons convenu de nous considérer en classe comme « étant tous des mathématiciens à part entière » cherchant à nous comprendre quand nous portons des jugements de validité différents sur un énoncé de la vie courante où la présence d’un « Si…, alors… » au sens trop mal défini, conduit les membres du groupe à avoir des avis divergents. Par exemple, « Si je lève le pied de l’accélérateur, la voiture ralentit » . Ce n’est qu’une fois convenu en pratique un même sens à donner au « Si…, alors… » en science (cela a pris plus d’un mois) que nous avons pu commencer à engager de vrais débats scientifiques en classe sur les savoirs du cours. Et là, je crois pouvoir dire que nous avons commencé à faire véritablement des mathématiques ensemble !

Ainsi, cet épisode du « Si… alors… » dans une classe de Sixième a joué un rôle de déclencheur qui a conduit Marc à se lancer quelques années plus tard dans un travail de recherche pédagogique dans le cadre de l’IREM de Grenoble. Cette recherche collective s’est étalée sur une trentaine d’années et a abouti au « débat scientifique » , objet de la suite de cet article¹.

Le débat scientifique

De quoi s’agit-il ? La meilleure façon de comprendre le concept est d’en suivre un exemple. Le thème du débat ci-dessous correspond au programme de Seconde de 2008. Il a été mené par Thomas Lecorre. Nous remercions l’IREM de Grenoble de nous avoir autorisés à reproduire intégralement² cet extrait de la brochure Le principe du « débat scientifique » dans un enseignement [1].

Présentation du contexte

Quand on veut faire un peu de géométrie déductive dans l’espace avec des élèves qui n’ont jusque-là fait que des manipulations d’objets de l’espace, le professeur se doit absolument de commencer par définir ou redéfinir un certain nombre de notions de base comme le parallélisme ou la perpendicularité, notions que les élèves connaissent donc déjà d’une certaine façon puisqu’ils les ont rencontrées et utilisées dans des démonstrations en géométrie plane.

Le professeur de la classe de Seconde que nous observons ici pourrait bien entendu commencer sa leçon en (re)donnant magistralement ces définitions, mais comme il a remarqué à maintes reprises qu’il prêchait dans le désert à chaque fois qu’il reprécisait/redéfinissait une notion dont les élèves avaient déjà entendu parler et qu’ils croyaient donc bien connaître, il adopte d’entrée de jeu la stratégie suivante : il demande aux élèves de proposer eux-mêmes des définitions qui prolongent à l’espace celles qu’ils connaissent en géométrie plane.

L’attente de ce professeur est alors que les élèves proposent les définitions qui leur paraissent les plus évidentes (celles de la géométrie plane) et qu’en exploitant ces définitions insuffisantes dans des situations assez simples de l’espace le débat fasse apparaître leur caractère par trop simpliste.

Script de la séance d’introduction d’une problématique de géométrie dans l’espace

Le professeur demande aux élèves de cette classe de proposer des définitions satisfaisantes à leurs yeux de deux droites parallèles et de deux droites perpendiculaires dans l’espace.

Proposition d’un élève :

Définition
Deux droites sont parallèles si elles ne se coupent pas.

Proposition d’un autre élève :

Définition
Deux droites sont perpendiculaires si elles se coupent à angle droit.

Le professeur (qui s’interdit absolument à ces moments cruciaux toute mimique et tout commentaire approbateur/désapprobateur qui indiquerait ce qui est pertinent/juste ou pas) propose sans sourciller d’adopter ces définitions pour tester si certains couples de droites qu’il va soumettre à la classe sont parallèles ou pas, et si d’autres sont perpendiculaires ou non.

Il trace donc au tableau un cube \(\mathsf{ABCDEFGH}\) et propose d’abord deux conjectures sur lesquelles les définitions proposées ne posent aucun problème de fond et par suite sur lesquelles la classe va pouvoir très vite se mettre d’accord.

Conjecture 1

Le vote :

• Vrai : 28.
• Faux : 2.
• Autre : 1.

Annah qui a voté Autre explique : « J’ai tendance à penser que c’est vrai, mais ça peut être un piège » .

Le professeur : « Tu dis donc que tu penses plutôt que c’est vrai, mais que comme tu me connais et que tu as déjà expérimenté mes conjectures, tu te méfies : ça peut être un piège ! »

(Visiblement Annah est à cheval entre deux contrats, celui du « débat scientifique » et le contrat scolaire classique. Elle ne sait pas ce qui doit primer : « ce qu’elle pense être vrai » ou « la réponse supposée attendue par le professeur » ? Elle a néanmoins assez confiance en ce dernier pour oser dire franchement quel jeu elle joue car elle sait qu’il réagira probablement plus par l’humour qu’en moralisant. En revanche elle va se faire vertement « balayer » par Chloé qui semble sûre de son coup et veut elle, à juste titre, qu’une question aussi triviale soit tranchée rapidement. Une deuxième remarque faite plus tard par le professeur pour bien montrer qu’il « ne tend pas des pièges pour prendre ses élèves en défaut » mais « pose des conjectures dont certaines sont vraies et d’autres fausses pour pousser chacun à plus travailler en réflexion » vont apparemment convaincre Annah qui ne cherchera plus dans la suite de « pièges » et rentrera davantage dans la recherche de « la vérité » ).

Chloé qui a voté Vrai intervient vigoureusement avant même que le professeur donne la parole : « C’est un carré donc les côtés sont parallèles ! »

Le professeur : « Tu parles de \(\mathsf{ABGF}\) ? Tu dis que c’est un carré et donc que les côtés opposés sont parallèles. C’est ça ? »

Chloé : « Oui, c’est ça ! »

Azédine qui a voté Faux (avec sa voisine Alizé) : « Pour un cube, il suffit de six faces et huit arêtes, et donc c’est pas forcément parallèle ou perpendiculaire. »

Le professeur : « Tu veux dire quoi ? »

Azédine : « Eh bien le cube peut être tordu ou bien même en morceaux, c’est alors toujours un cube et les droites ne sont pas parallèles. »

Le professeur : « Tu veux parler de ça : » et il dessine un « cube penché » .

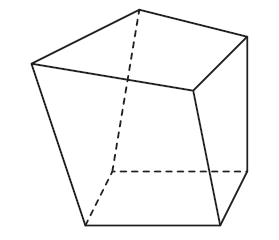
Rumeur dans la classe : ( « C’est pas un cube » , …)

Azédine : « Oui et comme ça elles se coupent, donc elles ne sont pas parallèles. »

Marine : « Ça c’est pas un cube, mais de toute façon, même comme ça elles ne se coupent pas ! »

Azédine : « Oui mais c’est des droites, alors on peut les prolonger ! »

Marine (qui a voté Vrai) : « Non, on peut pas les prolonger. »

Melissa (qui a voté Vrai) : « Mais votre cube c’est vraiment celui-là, ou bien on peut changer les lettres de place ? Parce que sinon je vote Faux »

(nous sommes là typiquement au cœur d’incongruités auxquelles on ne pense pas a priori, alors que le « débat scientifique » montre qu’elles existent presque toujours dans une classe ou dans un amphi. En principe, tout le monde est persuadé que dans une classe de Seconde les élèves savent ce qu’est un cube sans la moindre hésitation, et comme en plus ici le prof a dessiné un cube correct, on ne peut imaginer a priori qu’un seul élève ait en tête qu’un cube puisse être l’hexaèdre hétéroclite que le professeur a été amené à dessiner ensuite pour tenter de matérialiser la représentation du cube qu’Azédine semble avoir.

Le fait que le professeur ait accepté a priori — n’ait pas rejeté violemment — cette représentation erronée et le fait d’avoir proposé cette conjecture permettent juste à un tel anachronisme de se manifester au grand jour. Cela ralentit certes le déroulement du cours, mais laisse à penser aussi en contrepartie que si ce « bruit » ne s’était pas manifesté, n’avait pas été pris en compte, il pouvait interdire à tous ceux qui pensaient à quelque chose d’analogue de continuer à suivre en rationalité ce qui est proposé par le professeur ou par des pairs.

Comme toujours dans ce cas — vu le côté extravagant de la proposition — la classe proteste avec vigueur, le professeur laisse un peu la colère monter pour indiquer à tous qu’il va falloir remettre les pendules à l’heure et se donner une définition/convention commune car on ne peut débattre scientifiquement à partir d’un tel malentendu sur l’objet élémentaire cube, mais comme ce n’est pas le point essentiel sur lequel il veut faire travailler la classe, le professeur ne laisse pas le débat se poursuivre davantage sur ce point ; il l’arrête donc en utilisant son autorité magistrale pour déclarer le point de vue qu’il convient d’adopter pour poursuivre – par le ton qu’il adopte il fait comprendre que sauf objection très motivée d’un élève il n’y a plus lieu de débattre ici sur ce point précis. Le professeur tranche donc sans demander aux élèves leur avis sur ce point car s’il estime que ce premier débat a été utile pour lever un malentendu, il pense également que le laisser se poursuivre n’apporterait probablement rien de plus sur le fond et entraînerait une certaine lassitude de la part de ceux qui ont compris que le problème n’était pas là ; laisser poursuivre le débat sur ce point précis serait donc probablement nuisible à la compréhension commune et à la dynamique de la classe).

Le professeur intervient donc et explique qu’il faut se mettre d’accord sur les bases de la discussion : « qu’est-ce qu’un cube ? de quel cube parle-t-on ? Qu’est-ce qu’une droite dans l’espace ? » Il écrit donc magistralement :

Un cube est un solide fait de six faces carrées. Le cube dont on parle s’appelle \(\mathsf{ABCDEFGH}\) et les lettres sont exactement comme sur le dessin. Une droite dans l’espace est comme une droite du plan, elle est infinie.

Azédine et Alizé qui avaient voté Faux disent alors changer d’avis, et Annah maintient son vote Autre à cause de l’éventuel piège.

Pour bien marquer que le débat ne doit plus porter sur ce malentendu, le professeur conclut lui-même (ce qu’il s’interdirait de faire si le débat portait sur des contradictions de type logique) : « Ces deux droites sont bien, en effet, parallèles et cela a été parfaitement expliqué dans le débat : la face ABGF est un carré, et dans un carré les côtés opposés sont bien parallèles. On peut remarquer ici que pour savoir si les deux droites sont parallèles on utilise la face ABGF et finalement on se met dans
un plan, et cela nous permet de répondre à la question en faisant de la géométrie plane. »

Le professeur ajoute : « Annah tu as eu raison de douter, c’est vrai que souvent les évidences immédiates sont apparues après comme trompeuses. Tu exprimes le doute que nous avons tous un peu quand nous devons décider du vrai et du faux, mais ici tu vois, les droites ne sont pas parallèles parce que M. Lecorre l’a affirmé mais seulement parce qu’elles sont les côtés opposés d’un carré. »

Nouvelle conjecture

Conjecture 2

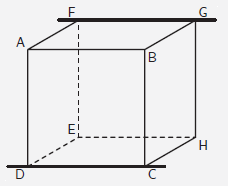Le vote :

• Vrai : 31.
• Faux : 0.
• Autre : 0.

Gregory : « On sait que \((\mathsf{AB})\) est parallèle à \((\mathsf{FG})\) et pour la même raison dans le carré \(\mathsf{ABCD}\), \((\mathsf{AB})\) est parallèle à \((\mathsf{DC})\) donc \((\mathsf{FG})\) est parallèle à la droite \((\mathsf{DC})\) » .

Le professeur reprend l’argument et demande si tout le monde est d’accord. Unanimité dans la classe.

(le professeur ne fait pas remarquer que la transitivité utilisée ici, qui est une propriété vraie du plan, pourrait ne pas demeurer valide dans l’espace : il fait comme si c’était effectivement évident, et se réserve de revenir plus tard sur ce type de « généralisation potentiellement abusive » . Le « plus tard » signifie : une fois précisément que les élèves auront rencontré de plein fouet des propriétés du plan qui ne se généralisent pas du tout à l’espace.

Ce professeur ne reprend pas ce point néanmoins important en bonne logique car il estime qu’il s’agit là d’un apprentissage méta qui aura beaucoup plus de chances d’être intériorisé par ses élèves si ce sont des expériences malheureuses qui leur montrent la nécessité de s’assurer que la généralisation est licite, plutôt que s’il réitère à chaque instant des conseils de précaution, conseils vite considérés par les élèves comme un tatillonnage/marotte de prof de mathématiques.)

Après ce très court débat, le professeur propose la troisième conjecture.

Troisième conjecture

Conjecture 3

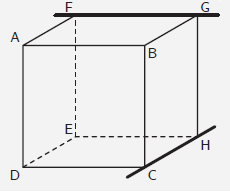• Vrai : 4.
• Faux : 18.
• Autre : 9.

Comme il y a un « vrai » problème, le débat s’engage véritablement :

Jonathan qui a voté Vrai déclare : « Les droites \((\mathsf{FG})\) et \((\mathsf{HC})\) ne sont pas dans le même plan, elles ne se coupent pas, donc d’après la définition elles sont parallèles. »

Tom qui a voté Autre dit : « Je suis d’accord mais pour moi elles sont aussi perpendiculaires si on les superpose. »

Chloé qui a voté Faux déclare : « \((\mathsf{FG})\) est perpendiculaire à \((\mathsf{GB})\) et \((\mathsf{GB})\) est parallèle à \((\mathsf{HC})\), donc \((\mathsf{FG})\) est perpendiculaire à \((\mathsf{HC})\) et donc elles ne sont pas parallèles. »

(tout comme dans le cas de la transitivité du parallélisme, comme personne ne conteste ce raisonnement de Chloé, le professeur ne force pas la discussion sur cet argument valide dans le plan bien qu’il soit litigieux dans l’espace, car il sait qu’un argument aussi faux refera nécessairement surface plus tard à un moment où la situation permettra peut-être à certains élèves de percevoir que ce raisonnement juste du plan n’est plus valide dans l’espace. Et ce sera alors ces élèves et non le professeur qui contesteront cette généralisation abusive, ce qui va progressivement permettre à la classe de s’investir d’une réelle responsabilité scientifique sur ce qui est vrai/faux, pertinent ou non.

On voit que contrairement à un cours classique où le professeur s’oblige à mettre tout de suite de l’ordre dans les propositions — les déclarer vraies/fausses, pertinentes ou non, etc. — au fur et à mesure qu’elles s’énoncent, ici le professeur laisse un certain nombre de propositions en jachère, même lorsqu’elles sont fortement erronées, afin soit de les faire ressurgir lui-même au moment où leur fausseté sera le plus éloquente pour la classe/amphi, soit pour bien montrer à la classe, à l’amphi que chacun doit en permanence exercer sa responsabilité scientifique, doit faire preuve de vigilance épistémologique, i.e. se poser la question : « ce qui est proposé ici et qui semble intéressant/utile, est-ce vrai ou faux, pertinent ou non, abusif ou pas, etc. etc. etc. ? » )

Marine qui a voté Faux soutient : « Il y en a une qui est horizontale et l’autre verticale, elles ne sont donc pas parallèles. »

Gregory qui a voté Vrai pointe le fond du problème : « le problème, c’est que la définition n’est pas commode. »

Azédine qui a voté Vrai explicite le « pas commode » : « Si on les met dans le même plan, alors c’est faux mais avec la définition, c’est vrai. »

Le professeur estime à cet instant que le débat a pour le moment joué son rôle essentiel : faire prendre conscience à l’ensemble de la classe que la définition des parallèles du plan ne suffit pas pour traduire ce qu’on veut désigner par le mot « parallèle » quand on est dans l’espace.

Il conclut alors : « Le problème avec cette conjecture, c’est que si on suit la définition de parallèles qu’on s’est donnée, alors on est bien obligé d’admettre que ces deux droites sont parallèles puisqu’elles ne se coupent pas. Du point de vue strictement logique ceux qui ont voté Vrai ont raison. Mais en même temps admettre que deux droites, dont l’une est verticale et l’autre horizontale, sont parallèles, ce n’est franchement « pas commode » comme le dit Gregory car ce n’est pas du tout notre perception du parallélisme. Et ceux qui votent Faux ont là une bonne raison de voter Faux. Mais cette raison n’est pas celle des règles de la logique que l’on s’est données. Enfin ceux qui ont voté Autre sont exactement entre ces deux propositions : ils ne peuvent pas se résoudre à dire la conjecture vraie, car ici leur idée du parallélisme est trop mise en défaut, ils ne peuvent pas non plus se résoudre à la déclarer fausse, parce qu’elle correspond à la définition. »

Le professeur insiste alors avec emphase : « Chacun voit bien donc que selon les règles de la logique, la conjecture est vraie, mais en même temps qu’il est insupportable de déclarer ces deux droites parallèles ! »

Puis il dramatise avec humour :

« Comment résoudre ce dilemme ? ? ? »

Réponse spontanée de beaucoup d’élèves : « on change la définition ! »

Le professeur en guise d’acquiescement demande à la classe de faire une nouvelle proposition de définition du parallélisme.

Proposition de définition 2 d’un élève
Deux droites sont parallèles si leurs vecteurs directeurs sont colinéaires.

Le professeur : « Avec cette nouvelle définition, que pensez-vous de la conjecture 3 ? »

et le cours se poursuit sur cette lancée !

Éléments d’analyse — généralisation

Si nous ne nous trompons pas trop dans notre analyse, ce qui se vérifiera par la suite lorsque d’autres indices montreront que les conceptions initiales trop naïves de parallèles ou de perpendiculaires ont pratiquement disparu (par exemple quand elles refont surface dans les propos de certains élèves – les conceptions erronées ne s’éradiquent pas d’un coup, elles refont toujours surface pendant un certain temps – elles sont tout de suite assez spontanément critiquées à bon escient par d’autres élèves), nous considérons que le « débat scientifique » a joué ici l’essentiel de son rôle, en ce sens que son coût (en particulier en terme de temps et d’investissement – en terme de fatigue aussi) n’est pas déraisonnable mais au contraire tout à fait justifié vu ce qu’il produit.

[…] il permet à beaucoup d’élèves de ne pas se désinvestir très rapidement de la situation, de ne pas abandonner très vite toute envie de faire les efforts de réflexion indispensables pour arriver à prouver proprement en géométrie dans l’espace, même lorsqu’il s’agit de résultats en apparence très élémentaires.

Après plusieurs années de pratique [du débat scientifique en classe] nous avons acquis la conviction que lorsqu’il s’agit d’aborder résolument un sujet conceptuellement délicat pour la majorité de nos élèves ou nos étudiants, nous limitons énormément le risque de nous retrouver seuls au bout d’un certain temps en train de brandir désespérément nos définitions, nos axiomes et nos démonstrations subtiles si, dès le départ de l’étude, nous avons su faire intervenir ces objets abstraits (initialement très formels pour les élèves) dans des débats où ils se concrétisent peu à peu parce que chacun peut les manipuler à sa façon : en les déformant en partie par des usages abusifs, puis en rectifiant les déformations qui produisent des contradictions, l’élève démonte ainsi quelques rouages de ces objets initialement très extérieurs à lui, peu à peu il se les approprie, il va alors pouvoir les faire intervenir à bon escient de son propre chef (et non sur commande : « en utilisant le théorème X montrez que … ! » ), voire dans certains cas, les transformer un peu pour les adapter à une situation où ils ne s’appliquent pas directement.

Un triple constat prometteur

[Ainsi], […] ce qui nous paraît le plus stable, le plus déterminant dans notre pratique régulière du « débat scientifique » , quand, pour pousser le trait, nous cherchons à dégager ce qui à lui seul justifierait qu’on continue à s’embarquer dans une telle aventure, ce qui ressort presque toujours en première place de ce questionnement, c’est finalement la répétition du triple constat suivant :
a) La pratique régulière d’une forme de débat nous offre à nous, professeurs, un outil chaque année un peu plus performant pour débusquer rapidement la nature et l’ampleur des malentendus souvent très importants qui s’installent inévitablement avec une bonne partie de la classe ou de l’amphi sur le sens profond de ce qu’on croit enseigner, et ce même lorsqu’on est persuadé avoir été très clair et très explicite pour éviter tous les pièges sur lesquels nos élèves/étudiants avaient buté les années précédentes.
Nous avons donc le sentiment de disposer là d’un moyen efficace pour pouvoir avancer dans l’exposé d’une théorie en cours sans être trop aveugle au niveau de la compréhension réelle de nos interlocuteurs, et même d’en avoir une vision assez objective.
b) Comme ces débats introductifs nous permettent de prendre conscience d’un possible décalage de sens profond avant que l’on ne soit allé trop loin dans l’avancée du cours, il nous est souvent possible à ce stade de problématiser positivement ce qui dysfonctionne (ce qui est en jeu au niveau de la perte de sens est encore assez nouveau pour le groupe classe ou amphi pour qu’on puisse en discuter librement sans que d’un côté certains s’ennuient car ils ont bien compris, et que d’autres aient à supporter la crainte de dire d’énormes bêtises devant les autres et la honte de montrer qu’ils n’ont pas encore compris ce que certains trouvent maintenant évident).
Quand on est au début d’une étude.
Quand on est au début d’une étude, « on a le droit de se tromper ! » , on ne se sent pas coupable de ne pas savoir ce qu’on devra bien maîtriser dans quelque temps !
Ce dernier aspect est essentiel pour libérer une parole d’élève qui soit spontanée, authentique et sincère.
c) La mise en débat des avis divergents produit alors assez souvent le petit miracle de la transformation de ce qui pouvait devenir un « drame » pour beaucoup en un moment de vrai bonheur collectif.
Le débat permet souvent que, pendant un moment au moins, sur un sujet précis important, tous partagent sans faux-semblants une même problématique et une problématique réellement scientifique.

Laissons la conclusion à Marc Legrand  [2] :

Sachant qu’à l’école tous les professeurs souhaitent faire réfléchir les élèves, mais qu’une fois répartis les différents chapitres du cours dans le calendrier on s’aperçoit que pour aucun d’entre eux on ne disposera du temps nécessaire pour s’engager dans un approfondissement épistémologique qui élargirait notre compréhension individuelle et collective du monde, on peut, en partant de l’idée qu’il y a toujours dans un programme des savoirs plus fondamentaux que d’autres, choisir ceux où l’on pense que l’on va pouvoir — si on se donne le temps — travailler le rapport collectif du groupe classe aux mathématiques comme une formidable occasion d’enrichir le rapport de chacun au monde. Et gageons alors que ce qu’on aura compris et intériorisé à leur étude sera suffisamment profond et intéressant pour rendre la classe ou l’amphi plus dynamique, plus compétent et efficace afin de pouvoir aborder sans en perdre le sens les autres savoirs auxquels on devra consacrer moins de temps.

Références

NDLR : Pour en savoir plus sur le débat scientifique, ses fondements et les concepts théoriques qui le sous-tendent (le contrat didactique, la consistance épistémologique), pour connaître les règles à instaurer pour le mettre en place dans
ses classes, nous vous conseillons les lectures suivantes :

• [1] Thomas Lecorre et al. Le principe du « débat scientifique » dans un enseignement. . 2011.↩
• [2] Marc Legrand. À la recherche d’une méthode pour mettre en évidence les savoirs fondamentaux. À paraître IREM de Grenoble, 2021.↩
• [3] Marc Legrand. Démocratie participative et construction collective d’un sens profond : « le débat où pour comprendre, on cherche à se comprendre ». À paraître . 2011.IREM de Grenoble, 2021.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Le groupe « débat scientifique en classe » de l’IREM de Grenoble, auteur de ce script d’introduction à la géométrie dans l’espace, était formé par Thomas Lecorre et Liouba Leroux, enseignants au lycée, et par Anne Parreau et Marc Legrand, enseignants de l‘université.

© APMEP Décembre 2021

---

1. Pour approfondir sur le « Si… alors… » , sujet tout à fait intéressant en tant que tel, on lira avec intérêt l’article de Zoé Mesnil page  58, construit notamment à partir de l’activité des Cosmonautes, un autre exemple issu des travaux de Marc Legrand.↩
2. NDLR : sauf mention contraire, toute la suite de cet article est extraite de la brochure [1], à l’exception des titres intermédiaires et de certains passages en couleur dus à la rédaction d’Au fil des maths..↩

---