Les mathématiques comme inspiratrices de la forme :
un petit panorama

Dans cet article, Olivier Longuet, qui dessine souvent des planches pour Au fil des maths, montre quelques exemples de bandes dessinées aux contraintes formelles inspirées des mathématiques, dans lesquelles il a puisé son inspiration.

Olivier Longuet

© APMEP Mars 2022

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Une planche de bande dessinée, avec ses cases rectangulaires, est souvent agencée de manière géométrique. Étant donné le nombre de strips¹ que doit contenir la planche, avec une largeur de gouttière constante entre les cases, avec une marge constante, si on veut des strips de hauteur constante, quelle doit être cette hauteur ? Souvent, le travail mathématique du dessinateur s’arrête là, et encore dans un album classique, il y a très peu de variations dans le nombre de strips. Aussi le dessinateur, si tant est qu’il ait fait le calcul une fois, n’y pense plus.

Mais il existe des auteurs qui utilisent les mathématiques en bande dessinée pour explorer les possibilités de narration et de visuel des planches.

À l’instar de l’OuLipo, qui utilise la littérature comme terrain de jeu en s’appuyant sur les mathématiques, certains auteurs de bande dessinée ont exploré les possibilités ludiques et narratives de leur médium et ont créé l’OuBaPo (Ouvroir de bande dessinée potentielle) au début des années 1990. Il y a d’autres ouvroirs dans des domaines variés (OuPeinPo en peinture, OuMuPo en musique, OuCuiPo en cuisine, etc.). Chacun d’eux propose dans son domaine spécifique des contraintes qui peuvent inspirer des créations originales. D’après Raymond Queneau, l’oulipien serait comme «un rat qui construit lui-même le labyrinthe dont il se propose de sortir».

Queneau avait proposé une table de Queneleiev, permettant de visualiser les contraintes créatrices sur les objets constitutifs de la littérature que ce soient des éléments linguistiques (lettre, syllabe, mot, phrase, paragraphe, chapitre) ou sémantiques (personnage, objet, événement, lieu, sentiment, durée) avec des considérations et des altérations sur la longueur, le nombre, l’ordre ou la nature. Comme la table de Mendeleiev, elle invite à la découverte de nouveaux objets.

Marcel Benabou, autre membre de l’OuLiPo a proposé un peu plus tard le Tollé (table des opérations linguistiques littéraires élémentaires), mettant encore plus en évidence les liens entre les textes et des opérations mathématiques (déplacement et forme, substitution, addition, soustraction, multiplication (répétition), division, prélèvement, contraction). Ainsi, La disparition de Perec peut être interprétée comme une soustraction de la lettre E.

Comme la bande dessinée est composée de textes et de dessins agencés dans des cases, il y a de nombreuses possibilités qui s’ajoutent à celles de la seule littérature. L’auteur peut opérer, en plus, des éléments de littérature avec des cases, des dessins, les couleurs, des bulles, ce qui augmente les possibilités de jeu. D’autant que l’aspect graphique invite à des manipulations géométriques variées.

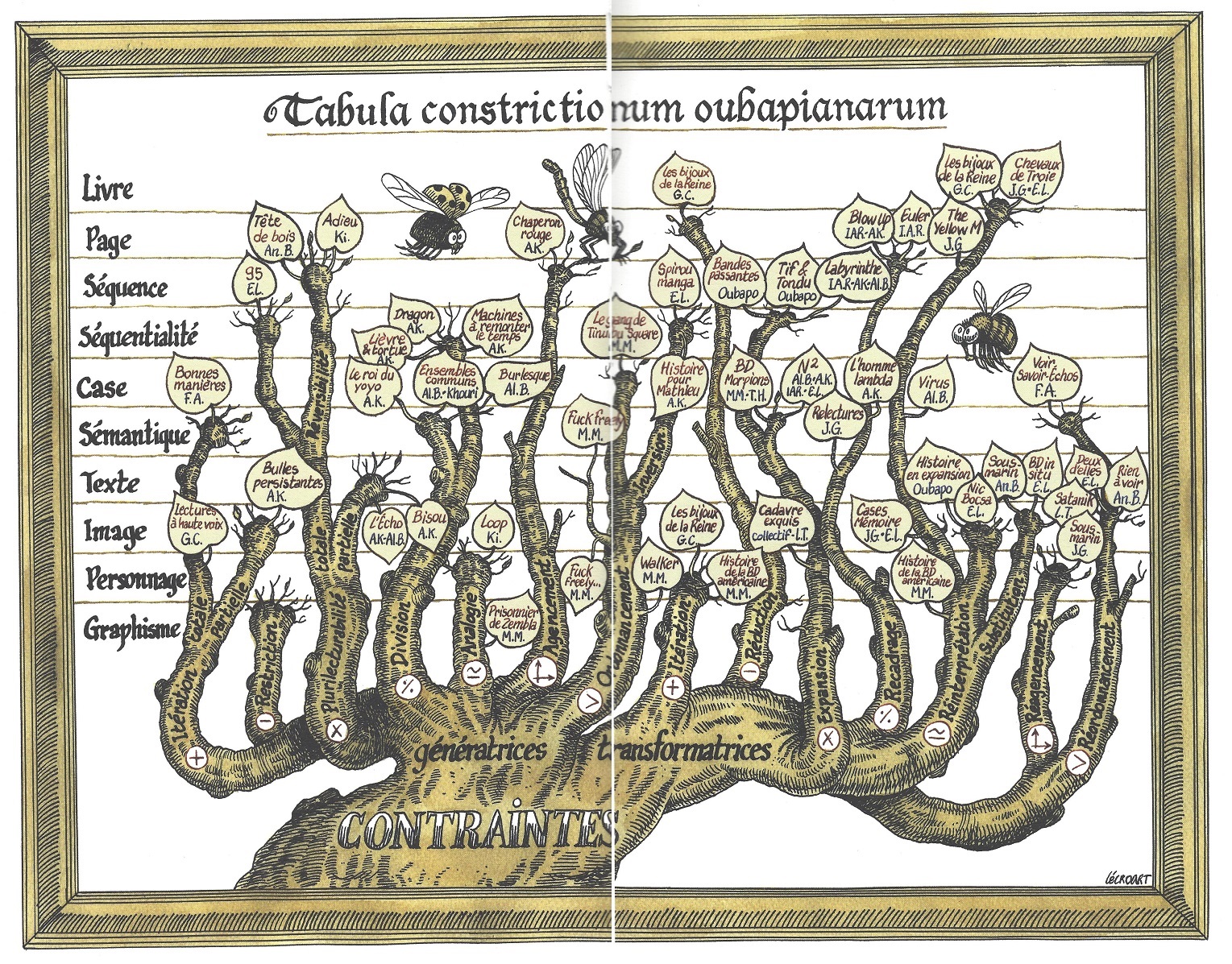
Certains auteurs de bande dessinée ont été davantage motivés par l’aspect ludique, par le jeu formel, que par l’aspect mathématique, mais la forme choisie évoquera des formes mathématiques et l’amateur de mathématiques y trouvera un intérêt sans que l’auteur ait envisagé cette grille de lecture. D’autres auteurs, comme Étienne Lécroart, Marc-Antoine Mathieu ou Ibn Al Rabbin sont tout à fait conscients de l’aspect mathématique de leurs défis et le théorisent à l’occasion. Dans l’arbre, on distingue les contraintes créatrices, qui inspirent une bande dessinée nouvelle et les contraintes transformatrices qui utilisent une bande dessinée existante pour en obtenir une nouvelle. Par exemple, la méthode \(\text{S}+7\) appliquée à une bande dessinée transforme tous les noms communs contenus dans les bulles mais peut aussi modifier les objets dessinés sur la planche en transformant le nom qui le désigne en nom \(\text{S}+7\), c’est à dire le 7^e substantif qui le suit dans un dictionnaire choisi. On obtient une nouvelle bande dessinée très décalée. On peut y voir une application de la translation dans l’ensemble des noms communs.

Voici quelques exemples remarquables de bandes dessinées à contrainte inspirée des mathématiques.

Le premier exemple historique est Upside Down de Gustave Verbeck, publié dans des journaux américains en 1903, alors que la bande dessinée en était à ses débuts. Il y a une soixantaine de planches autonomes comportant six vignettes carrées de taille identique, placées en gaufrier, racontant les histoires d’une petite fille et de son grand-père qui rencontraient souvent des animaux monstrueux. Pour lire une page, on commence par lire normalement les six cases, puis pour poursuivre l’aventure, il faut retourner la page à 180°, et les cases prennent un tout autre sens. La première case devient la douzième et dernière case, la deuxième devient la onzième, etc. Les images à double sens existaient déjà au XIX^e siècle mais en faire une bande dessinée est un véritable exploit.

L’édition française (Pierre Horay, 1977) est difficilement trouvable. Sa couverture présente un dessin qui peut être interprété de deux manières différentes.

Cette bande dessinée met en scène deux personnages, une petite fille avec une grande robe et un bonnet à franges assez ridicule et un vieil homme avec un grand chapeau. Après retournement, ils échangent leur rôle.

À noter qu’à l’origine, la planche avait un format à l’italienne (format paysage) et que la planche a été remontée en France pour un format portrait, mais le procédé fonctionne toujours.

Ordre de lecture des cases :

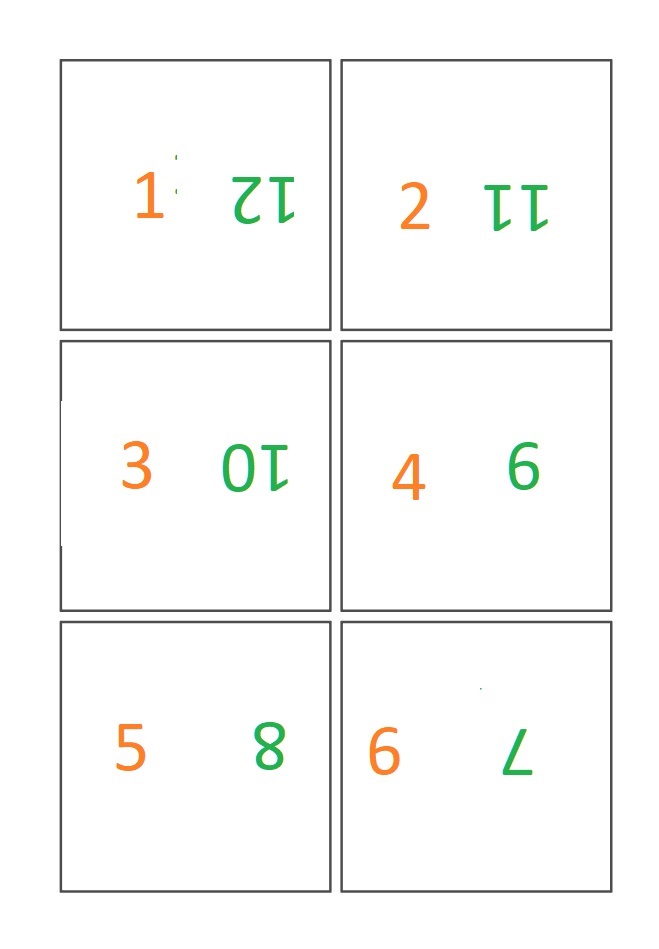
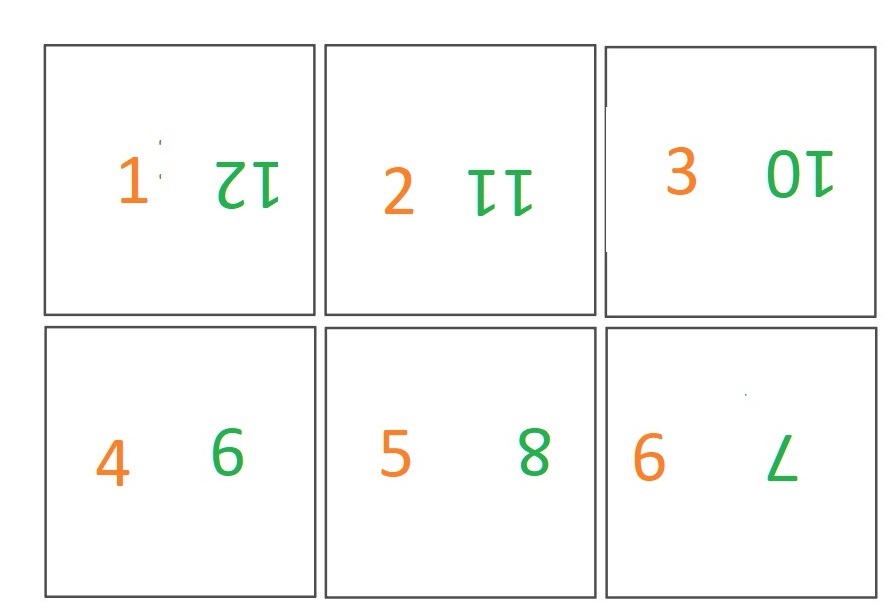
La bande dessinée en était encore à ses tous débuts, l’usage de la bulle n’était pas encore très répandue. S’il avait fallu introduire des bulles, elles auraient sans doute dû être lisibles dans les deux sens, avec des significations différentes, avec des ambigrammes.

Le retournement de la page amène la plupart du temps un retournement de situation.

Au cours de l’histoire de la bande dessinée, il y a eu d’autres jeux formels, mais le premier ouvrage revendiqué oubapien date de 1991 : il s’agit de Moins d’un quart de seconde pour vivre de Lewis Trondheim et Jean-Christophe Menu (deux artistes fondateurs de l’Association) qui est composé de cent strips de quatre cases et d’en tout et pour tout huit dessins différents, répétés pour donner lieu à un univers cohérent. Si cette œuvre fondatrice a l’air d’un jeu, ce jeu n’a pour l’instant rien de mathématique.

En 1997, le premier ouvrage collectif de l’OuBaPo sort et propose un premier panorama de bandes dessinées avec des contraintes formelles, préexistantes ou créées pour l’occasion.

L’amateur de mathématique remarquera en particulier la construction géométrique à la manière d’Escher des planches de Killofer, les BD dés Après tout, tant pis ! d’Anne Baraou et Corinne Charmeau, aux \(3 ! \times 6^{3}\), soit histoires possibles, utilisant des astuces syntaxiques proches de celles de Cent mille milliards de poèmes de Raymond Queneau, ainsi que la bande dessinée en tireur à la ligne, Grabuge Galactique de Jean-Christophe Menu et Étienne Lécroart.

Le tireur à la ligne peut être considéré comme un jeu qui se joue par exemple à quatre après une bonne soirée : chaque joueur écrit sur une feuille préparée deux phrases \(\mathrm{A}_{1}\) et \(\mathrm{A}_{2}\) racontant ensemble une courte histoire, puis passe à son voisin qui écrit trois phrases \(\mathrm{B}_{1}\), \(\mathrm{B}_{2}\), \(\mathrm{B}_{3}\) qui s’intercalent de manière à ce que \(\mathrm{B}_{1}\), \(\mathrm{A}_{1}\), \(\mathrm{B}_{2}\), \(\mathrm{A}_{2}\), \(\mathrm{B}_{3}\) raconte une histoire cohérente, puis on continue avec un troisième joueur C qui ajoute une phrase au début, entre chaque phrase déjà écrite et une à la fin, puis un quatrième joueur D qui fait de même. On relit alors les quatre versions et on peut apprécier les changements de situation et de sens que cela provoque, c’est souvent très drôle avec un peu d’entraînement. Songez que les phrases \(\mathrm{A}_{1}\) et \(\mathrm{A}_{2}\) se trouvent perdues au tiers et au deux tiers de la feuille, perdant toute leur importance au début, de nouveaux personnages apparaissent, qui prennent une importance de plus en plus grande dans le récit, des phrases prennent une toute autre signification dans un autre contexte.

Grabuge Galactique part de ce principe, en remplaçant les phrases par des cases de bande dessinée de même taille placées en gaufrier. À cela s’ajoute une seconde contrainte qui a priori semblerait compliquer le jeu mais en fait, libère la créativité : les cases A auront des dialogues qui commenceront par la lettre A, les cases B par la lettre B, etc. La contrainte libère la créativité, disais-je : si on réussit à respecter cette contrainte, on a déjà réussi une partie du contrat qu’on s’est fixé, et la plupart du temps, le résultat est drôle pour l’auteur mais aussi très satisfaisant et drôle pour le lecteur. On pourra se poser des questions mathématiques à propos de cette bande dessinée : Grabuge Galactique s’arrête comme son nom l’indique à l’étape G. En regardant la mise en page, combien de pages fait la bande dessinée compilant toutes les histoires créées ? Et pourquoi s’être arrêté à la lettre G et pas à la lettre Z (outre la difficulté de faire des phrases commençant par K ou X) ?

Un petit exercice de formalisation mettant en scène des suites arithmético-géométriques.

Étienne Lécroart, l’un des animateurs les plus imaginatifs et prolifiques de l’OuBaPo, est attiré au départ par l’aspect ludique de ces contraintes formelles, par exemple les planches à lectures multiples, comme cette planche, où après chaque case, on peut lire une des cases à droite qui sont liées par un côté ou un coin en suivant une des flèches proposées. Il y a bien 68 histoires possibles.

Y a-t-il un rapport entre cette planche et la suite de Fibonacci ? À vous de la découvrir…

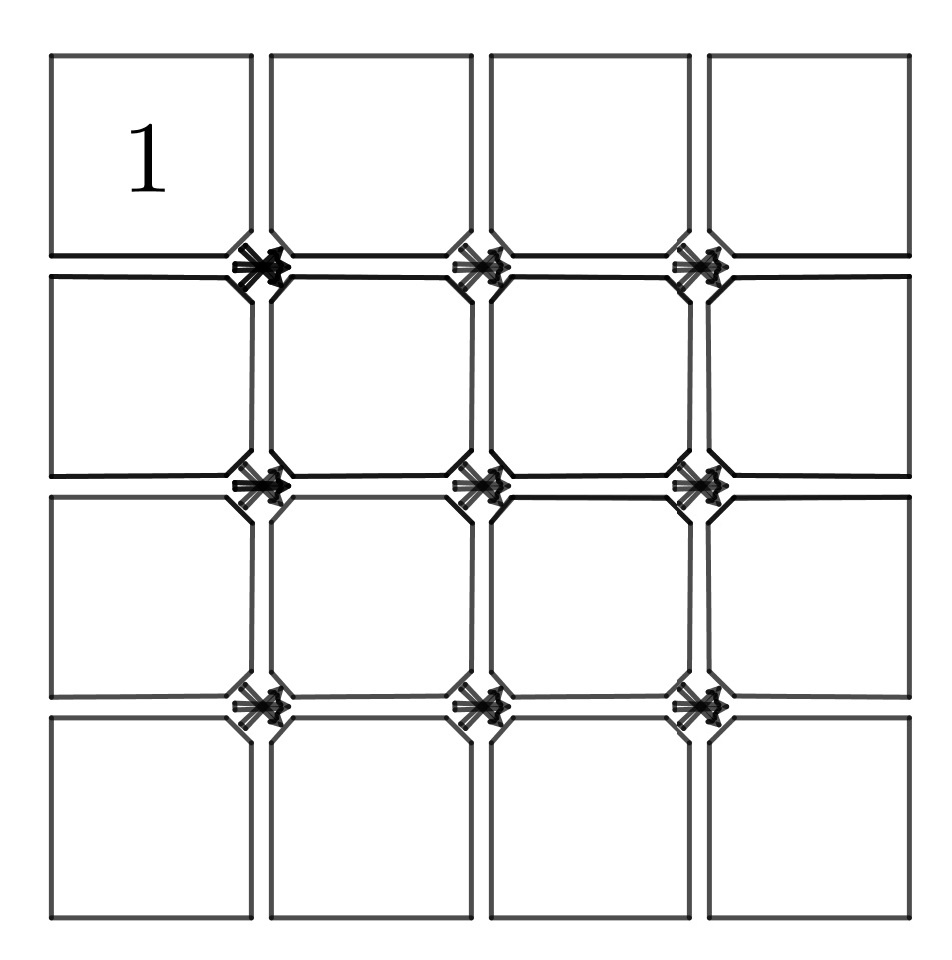
Le travail de Lécroart, de façon analogue à Escher, est remarqué par des mathématiciens, et cette ouverture lui donne d’autres pistes de recherche passionnantes, dont on peut voir l’étendue dans le très riche Contes et Décomptes, paru à L’Association ou sur son site internet . Il est aussi membre de l’OuLiPo depuis 2012.

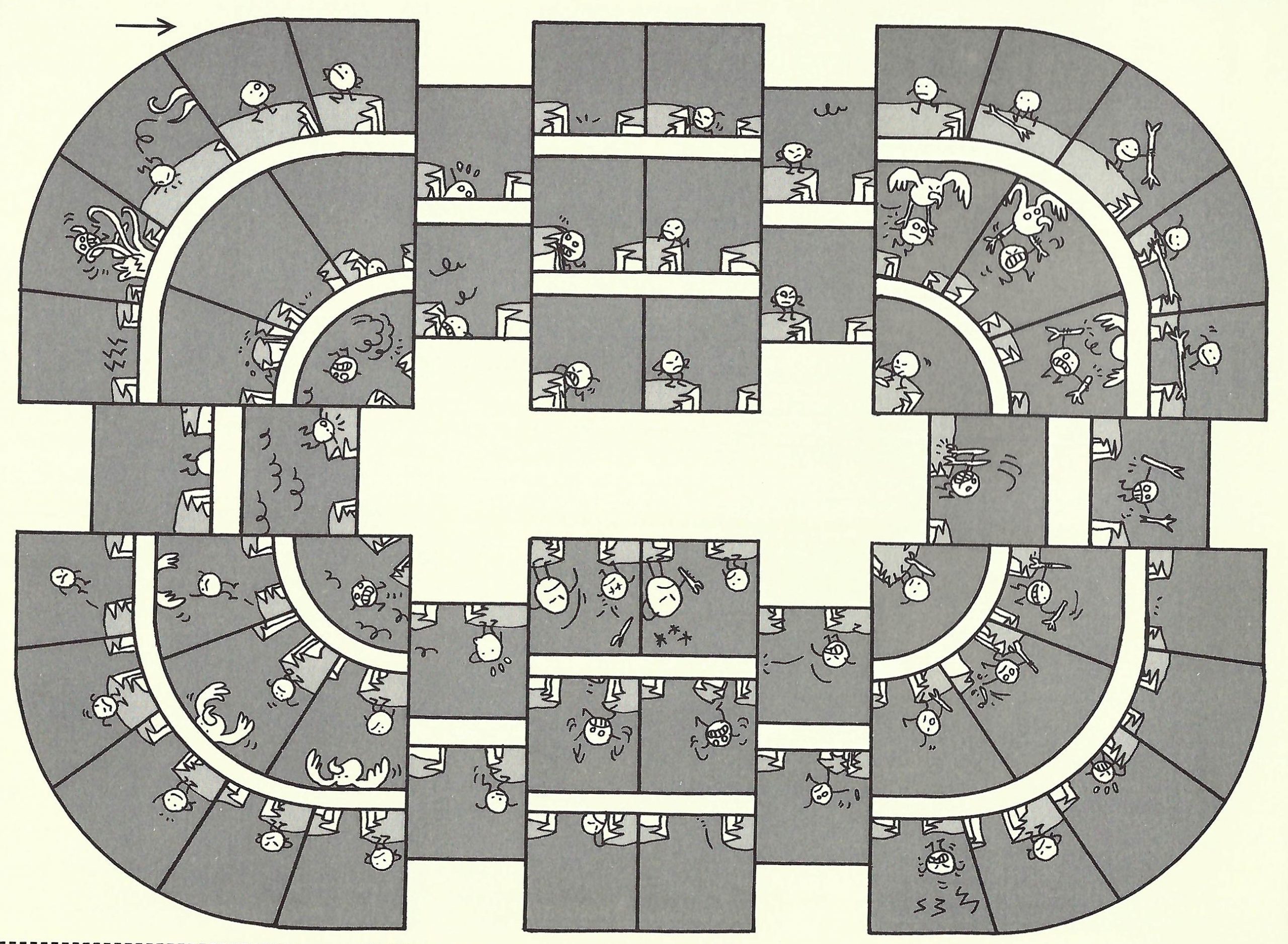
Ce que les Oubapiens appellent la plurilecturabilité amène de beaux exercices de combinatoire, comme cette planche remarquable de Lewis Trondheim (oubapo 3), en forme de morlaque (mord la queue, une bande qui revient à son point de départ) ou encore le très impressionnant Vanille ou Chocolat (éditions Cambouis), une sorte de BD dont on est le héros, élaboré à l’aide d’un algorithme très complexe par Jason Shiga, diplômé en mathématiques pures à Berkeley.

Un autre auteur qui utilise beaucoup les mathématiques dans ses œuvres est Marc-Antoine Mathieu, surtout dans sa  série Julius Corentin Acquefacques, prisonnier des rêves. Cette série, qui est une immense mise en abyme a  beaucoup d’angles de lecture, on pense à Kafka, à Borges, au théâtre de l’absurde, et il y a de nombreuses  considérations mathématiques, des planches fractales, des expérimentations à l’aide de découpages qui peuvent être formalisés avec des équations paramétriques.

Références

1. Collectif. Oubapo oupus 1, 2, 3, 6. l’Association.
2. Étienne Lécroart. Cercle Vicieux. l’Association.
3. Étienne Lécroart. Comptes et décomptes. l’Association.
4. Étienne Lécroart. Bandes de sonnets. l’Association.
5. Lewis Trondheim. Ovni. Delcourt.
6. Anne Baraou et Vincent Sardon. Coquetèle. l’Association.
7. Ibn Al Rabin. Splendeurs et misère du verbe. l’Association.
8. Collectif. Scroubabble. l’Association.
9. Marc-Antoine Mathieu. Julius Corentin AcqueFacques, prisonnier des rêves (7 tomes). Delcourt.
10. Gustave Verbeeck. Dessus dessous. Pierre Horay.
11. Luc Schuiten et François Schuiten. NogegoN. les humanoïdes associés.
12. Ibn Al Rabin. Considérations sur les flèches de l’amour. Atrabile.
13. Jason Shiga. Vanille et chocolat. Cambouis.
14. Renaud Farace et Olivier Philipponeau. \(\pi\)ramide. the hoochie coochie.

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Olivier Longuet enseigne les mathématiques au lycée Alain Chartier de Bayeux. Il est membre de l’équipe de rédaction d’Au fil des maths et notamment l’auteur de certaines des illustrations. N’hésitez pas à parcourir son blog .