HowMany, le calcul mental par l’image

Dans cet article, Alexandre Desmarest vous présente HowMany, un nouvel outil pédagogique qu’il a créé, dédié au calcul mental. HowMany s’adresse à tout public dès l’école élémentaire et peut se décliner sur tout type de support (papier, diaporamas vidéoprojetables, application gratuite sur tablette ou ordiphone).
À vous de jouer !

Alexandre Desmarest

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

Le calcul mental par l’image

HowMany est un concept innovant et intuitif, dont l’objectif vise à améliorer les compétences des élèves dans le domaine du calcul mental de la maternelle à la classe de 6^e.

HowMany propose des « dessins à calculer », constitués d’objets et de symboles empruntés au quotidien, qui amènent les élèves à élaborer eux-mêmes une stratégie correcte pour trouver, le plus rapidement possible, les nombres qui se cachent derrière les dessins.

Figure1. Exemples de « dessins à calculer »

En fonction du niveau ou du type de dessin, des aptitudes et connaissances mathématiques disponibles de chacun, les stratégies adoptées peuvent être très différentes les unes des autres.

Par exemple, pour trouver le nombre d’anneaux, un élève pourrait :

dénombrer les anneaux par comptage de un en un : « 1, 2, 3, …, 15 » ;
dénombrer par paquets de cinq : « 5, 10, 15 » ;
calculer « 5 + 5 + 5 » ;
modéliser le problème par \(3 \times 5\) et faire appel à sa mémoire des tables de multiplication ;
etc.

Évidemment, l’enjeu est d’amener les élèves à abandonner les procédures de comptage au profit des procédures de calcul. La confrontation aux procédures d’autres élèves et/ou l’utilisation d’un timing suffisamment court permettront de montrer que le dénombrement par comptage fait perdre un temps précieux !

Pourquoi HowMany ?

Développer l’aptitude à modéliser un problème basique¹

Si le graphisme de chaque dessin joue un rôle essentiel pour le rendre attractif, l’objectif principal de l’image est d’abord de signifier un calcul lié à une ou plusieurs opérations. Or, donner du sens aux opérations via une représentation imagée permet en particulier de développer sa capacité à associer la « bonne » opération à une situation donnée.

L’origine de la difficulté de l’élève à associer la « bonne » opération à un problème élémentaire fait l’objet de nombreux débats. Une hypothèse récurrente explique que cela pourrait provenir d’un manque d’expérience dans l’analyse, l’observation et la compréhension de situations de la vie quotidienne faisant intervenir l’une des quatre opérations élémentaires (raisons qui peuvent être d’ordre culturel, ou liées au développement intellectuel de l’enfant). Revenir sur cette aptitude le plus tôt possible, la travailler régulièrement est primordial dans la mesure où elle est nécessaire à une bonne appréhension de certaines notions mathématiques abordées par la suite.

De nombreux réflexes pédagogiques (comme celui qui consiste à illustrer un problème par un schéma) permettent de revenir naturellement sur ces aptitudes. Néanmoins, l’expérience montre que ces pratiques doivent être fréquentes et construites à partir de beaucoup d’exemples pour espérer ancrer des mécanismes durables dans le temps.

La pratique régulière de HowMany en classe, ainsi que sa pratique autonome via la tablette ou l’ordiphone, semblent apporter une réponse satisfaisante à ce besoin. L’application permet à l’élève de revenir seul, par épisodes plus ou moins longs, sur des jeux proposant chacun plusieurs dizaines de configurations différentes. C’est donc en jouant que les réflexes vont se construire et que l’aptitude se développera de façon pérenne.

Donner du sens à un calcul

Les images proposent des associations d’objets du quotidien, ce qui permet aussi de donner du sens au calcul demandé, au contraire des questions du type « opérande opérateur opérande » (par exemple \(7 + 8\) ou encore \(5 \times 6\)), par ailleurs indispensables mais où l’écriture chiffrée fait perdre au calcul son caractère concret. Cependant, loin d’être opposées, ces deux activités (représentation visuelle et représentation chiffrée) restent complémentaires. L’expérience montre que l’étape visuelle s’avère même indispensable pour certains élèves qui éprouvent des difficultés à passer à l’étape d’abstraction.

L’approche visuelle permet aussi de développer le sens de la quantité comme on va l’observer dans l’exemple qui suit.

Un élève de CM2 devant réaliser une multiplication posée au tableau, donc amené à mobiliser ses tables, affirme soudainement à voix haute que « \(9\times7=23\) ». Après que l’enseignant a rectifié l’erreur, l’élève ajoute : « je savais bien que cela se terminait par un \(3\) ! ».

Tout est dit. L’automatisation combinée à une mauvaise mémorisation l’emporte sur la notion de quantité et l’erreur produite est aberrante.

Le dessin d’un calendrier comportant neuf semaines (figure 2) pourrait lui fait prendre conscience de l’ordre de grandeur du résultat attendu.

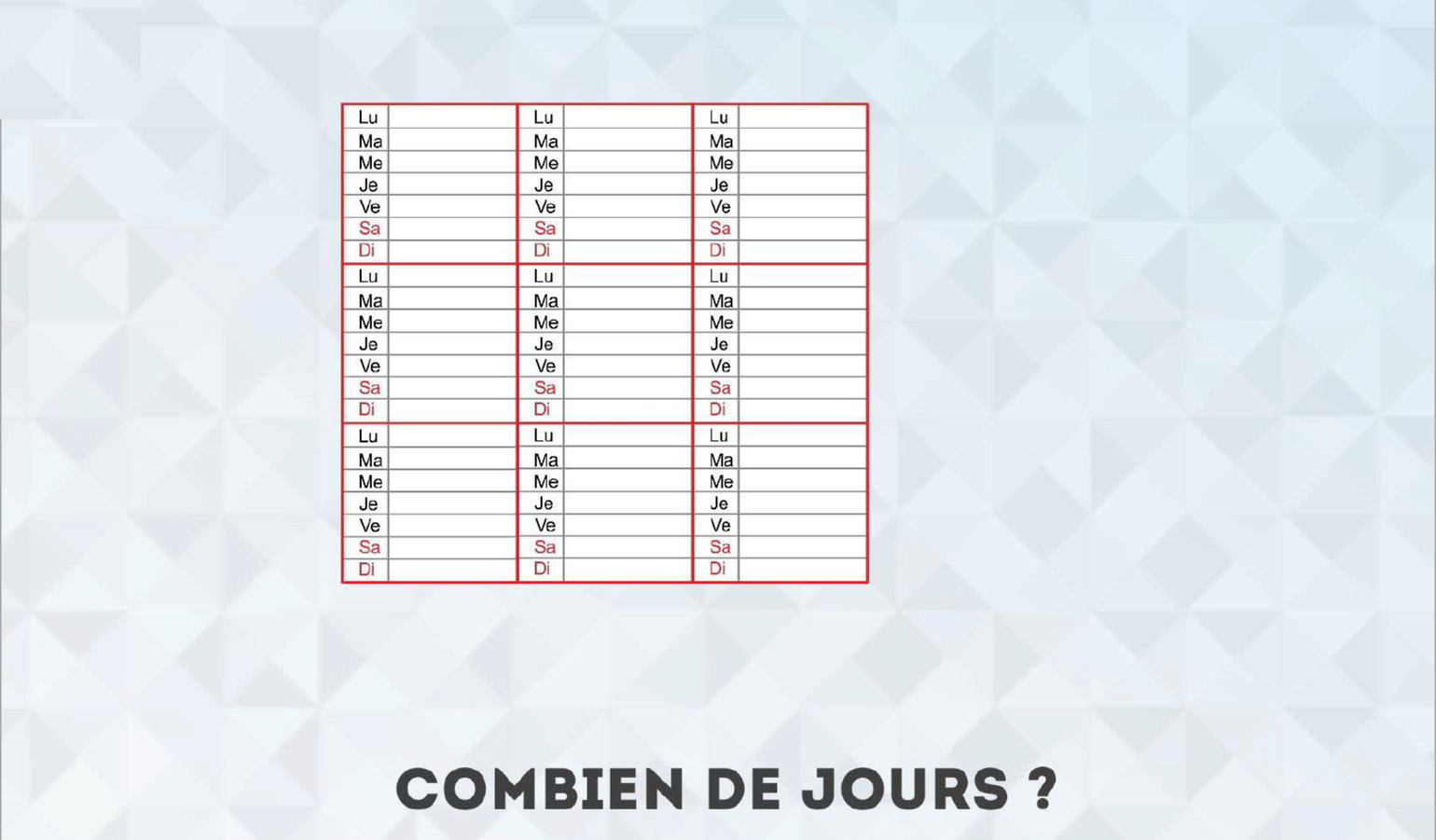
C’est ce qui s’observe assez souvent lors d’expérimentations de la pratique quand, face au dessin, l’élève s’apprêtant à fournir une réponse s’arrête net dans son élan, expliquant après coup qu’il « allait dire une bêtise ».

Modéliser et contribuer à la mémorisation de faits numériques

De nombreux élèves ne parviennent pas à mémoriser de façon satisfaisante les tables de multiplication malgré un entraînement répété. Une représentation mentale des nombres combinée à la compréhension des opérations en jeu peut alors être nécessaire. La pratique lui permet de construire du lien entre les représentations imagées du nombre et les représentations liées aux codages issus des systèmes de numération, chiffrée ou verbale, favorisant ainsi le processus de mémorisation.

Analysons le comportement de l’élève, face à l’exemple suivant.

Première étape : visualisation de 8 chaises ayant toutes 4 pieds permettant d’amener à la modélisation « \(8 \times 4\) ».
Si cette étape pose problème, c’est l’occasion de revenir sur l’addition itérée où l’on met en évidence, dessin à l’appui, le passage du « \(4 + 4 +\cdots+ 4\), huit fois » au « 8 fois 4 ».
Suivant le dessin proposé, le niveau de l’élève ou de la classe, cette étape peut s’avérer plus longue que celle qui suit.
L’objectif pourrait d’ailleurs être pour certains élèves de travailler dans un premier temps uniquement cette étape en leur demandant d’associer la bonne multiplication, sans attente de résultat.
Deuxième étape : combien font \(8 \times 4\) ?
Certains élèves ont mémorisé le résultat et répondent directement « 32 ».
Pour d’autres, il s’agira de (re)construire ce fait numérique.
Seul pendant la recherche ou avec l’aide de l’enseignant lors de la correction, l’élève peut recourir à de nombreuses stratégies, dessin à l’appui. Elles sont variables selon le niveau de l’élève, les méthodes ou réflexes déjà acquis.
Quelques exemples :
- compter les pieds un à un. Fastidieux mais nécessaire pour certains élèves : le labeur permettant de retenir le résultat final !
- compter de 4 en 4 : 4, 8, 12, 16, … L’élève retiendra le résultat en mobilisant un acquis qu’il maîtrise ;
- grouper en rangées puis effectuer le double de 16 : l’occasion de réinvestir ce qui a été travaillé sur les quantités doubles ;
- dénombrer de 8 en 8, pour ceux qui voient deux fois deux chaises à gauche comme à droite…

Cette situation souvent rencontrée sur le terrain illustre bien la complémentarité de ces deux étapes : l’image est projetée en classe entière et c’est au plus rapide de proposer une réponse.

L’élève A qui a réussi à modéliser plus vite que les autres mais dont le résultat non mémorisé ne vient pas, prend quand même la parole le premier pour dire : « 8 fois 4 ».

L’élève B qui n’a pas eu le temps de modéliser mais qui a mémorisé le résultat de \(8\times 4\) profite alors de la proposition de l’élève A et enchaîne aussitôt : « 32 ».

Dans cette situation, le collectif montre toute son importance et tout le monde y gagne : l’élève A qui « intégrera » mieux le 32 que vient de lui apporter son camarade, l’élève B qui comprend toute l’importance de la modélisation et l’enseignant qui profite de cette occasion pour mettre en évidence les différentes étapes du cheminement ayant permis l’obtention collective du résultat.

S’entraîner aussi à résoudre des problèmes complexes

Lorsque la résolution de problèmes simples (en une étape, briques élémentaires sur lesquelles pourront s’appuyer les élèves pour résoudre les problèmes en plusieurs étapes) a été suffisamment travaillée et que la maîtrise des faits numériques (tables notamment) est suffisante, il devient alors intéressant de proposer des tableaux plus complexes amenant l’élève à mobiliser d’autres compétences que l’observation et la mémoire.

Par exemple, les deux problèmes suivants (figures 4 et 5) ont fait l’objet d’expérimentations en classe.

Ici, la stratégie la plus retrouvée est la suivante : l’élève compte d’abord les triangles puis effectue une première multiplication. Il procède ensuite de la même manière avec les carrés pour finalement additionner les deux produits : \(8 \times 3 + 4 \times 4 = 40\).

Un autre groupe préfère remarquer que dans chaque colonne, il y a autant de triangles que de carrés avant de terminer par un produit \((4 + 3 + 3) \times
4 = 40\). Ce qui sera, après discussion, la méthode la plus efficace.

Ce qui ne nous empêchera pas, bien au contraire, de valoriser les méthodes plus singulières comme celle de cet élève qui explique son procédé comme suit.

« Un carré et un triangle ça donne 7 ; et comme en haut il y en a quatre, j’ai d’abord fait : \(7 \times 4 = 28\).

Ensuite, j’ai remarqué qu’il ne restait que des triangles en bas : j’ai donc fait \(4 \times 3 = 12\). Et j’ai fait à la fin \(28 + 12 = 40\). ».

Dans ce deuxième exemple, les stratégies sont également variées même si l’on trouve majoritairement ces deux-là.

Méthode 1 : l’élève calcule d’abord le nombre de paires grises (petites piles), \(3 \times 4\) paires grises, soit 12 paires grises ; puis les autres (grandes piles), \(3 \times 6\) paires, soit 18 paires.
Ensuite il additionne et multiplie par 2.
Bilan : \((3 \times 4 + 3 \times 6) \times 2 = 60\).
Méthode 2 : l’élève remarque qu’à côté de chaque grande pile il y a en a une petite (regroupement global).
Bilan : \((3 \times 10) \times 2 = 60\).

Modalités d’utilisation de HowMany en classe

Les modalités d’utilisation avec les élèves sont multiples. Et aujourd’hui, l’un des objectifs majeurs pour notre collectif est précisément d’échanger autour de toutes ces modalités, de partager les expériences de chacun dans nos classes, de tenter de dégager des protocoles plus ou moins pertinents suivant la configuration utilisée.

Questions flash

Les premiers retours d’expérimentation sur des classes euroises (essentiellement le cycle 2 de la circonscription de Vernon) montrent que la vidéoprojection de HowMany en classe entière au moyen de l’application dédiée ou à partir de diaporamas (disponibles directement sur le site) reste pour l’instant la modalité privilégiée.

Dans l’exemple suivant, face à une classe de Sixième, l’enseignante propose un seul dessin au début de chaque séance. La consigne est la suivante: « Tu as une minute pour trouver le résultat et être capable de l’expliquer à toute la classe ».

Cette modalité fournit l’occasion de mobiliser les automatismes, de réfléchir à la stratégie à employer, mais aussi d’apprendre à communiquer une démarche.

Une fonctionnalité sur l’application en ligne, non encore développée (car actuellement en chantier), devra permettre à l’utilisateur de déplacer les différents objets à l’aide du stylet (ou à la main sur la tablette) afin de mettre en évidence les regroupements possibles.

Match par équipe

Une configuration que j’ai personnellement appréciée est celle du « match par équipe ». En voici le déroulement : des équipes de quatre élèves maximum (pour faciliter la gestion) sont formées tandis que le tableau de classe est divisé en deux :

la partie « scores » comptant autant de colonnes que d’équipes et dans lesquelles les points sont inscrits ;
la partie « dessins » sur laquelle le diaporama est vidéoprojeté.

Pour chaque dessin, la consigne est la même : « Le premier qui fournit une réponse ! ». Si celle-ci s’avère exacte, l’équipe gagne les points (plus ou moins selon la difficulté du dessin). Dans le cas contraire, elle voit son score diminué du nombre de points équivalent, contraignant ainsi chaque équipe à ne pas se précipiter et à se consulter avant de proposer un résultat.

Cette modalité, basée notamment sur la rapidité, est intéressante pour favoriser l’acquisition des automatismes. Par exemple, dénombrer les objets un à un ou de deux en deux devient vite moins efficace face à une équipe qui connaît ses tables de multiplication.

HowMany sur tablette

L’usage des supports numériques constitue un mode d’utilisation privilégié dans un cadre pédagogique tourné vers le travail en autonomie.

L’actuelle version propose deux modes de jeu :

Le mode APPRENDRE, entièrement paramétrable avec des thèmes spécifiques (addition, multiplication, double, triple, numération, volumétrie, etc.), constitue pour ainsi dire la pierre angulaire de l’outil enseignant. En évolution constante, cette rubrique fait régulièrement l’objet de nouvelles versions proposant des thématiques inédites, originales, pour la plupart issues d’échanges entre acteurs du milieu éducatif acceptant d’apporter leur pierre à l’édifice.

Figure 8. Page d’accueil du mode APPRENDRE.
Le mode JOUER, où le joueur pratique l’exercice du calcul mental de manière complètement libre, en temps limité ou pas, dans un univers de jeu familier (débloquer des niveaux, améliorer ses scores, obtenir un maximum d’étoiles par niveaux, etc.).

Exemple d’un problème du thème « tables de multiplication » (mode APPRENDRE) :

Figure 9. Les boules de glace, avec correction.

La rosace de chiffres, située en haut à droite sur l’écran, permet de sélectionner les tables sur lesquelles travailler. Sur l’écran (figure 9), seules les tables 2 et 5 sont activées.

Le centre de la rosace, également paramétrable permet le réglage de la vitesse du timing. C’est ici que l’on règle la vitesse, pouvant même choisir une vitesse nulle afin de travailler sans chronomètre. Sur l’écran (figure 9), la vitesse est en mode normal (cool).

Il est important de noter qu’en mode APPRENDRE, une correction est systématiquement apportée aussitôt l’erreur commise et ceci afin de favoriser le processus d’automatisation du calcul. L’application propose une « phrase-lien » permettant d’associer la représentation imagée à l’écriture chiffrée (en mode JOUER, cette correction est répertoriée dans un journal d’erreurs consultable en fin de partie).

Le « tabloscope » permet de visualiser le niveau de l’utilisateur relativement à chaque table, mettant en évidence par exemple celles qu’il faut absolument retravailler.

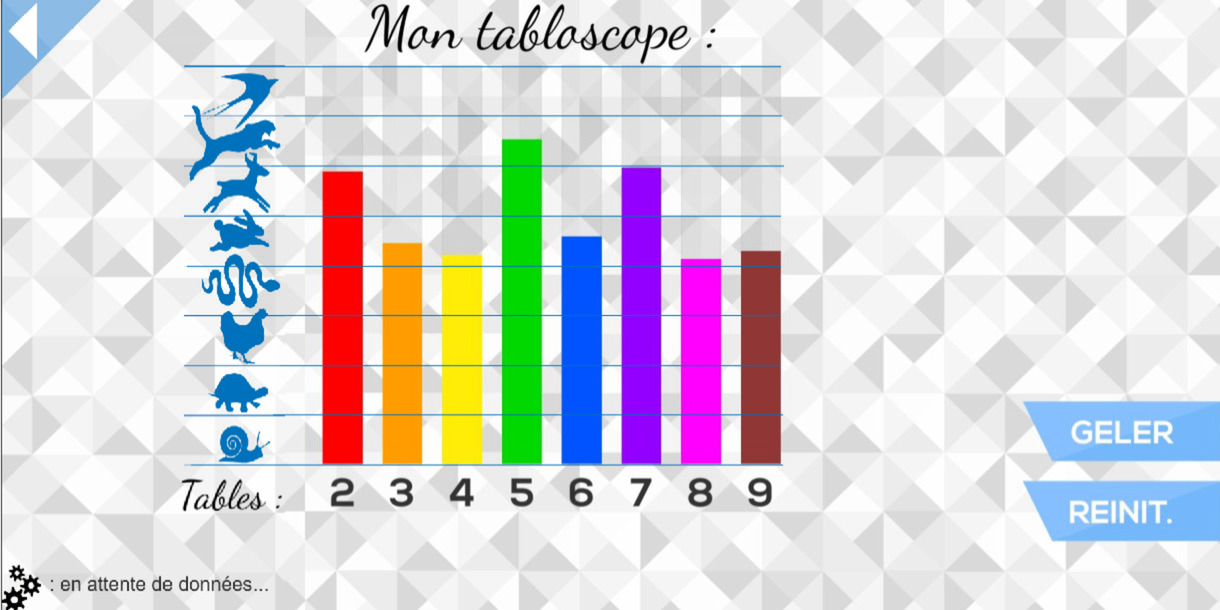
L’application sur ordiphone se présente de la même manière que celle sur tablette avec son mode APPRENDRE et son mode JEU. Aussi, les modalités décrites dans les paragraphes précédents restent tout à fait valables pour ce support.

Conclusion

HowMany offre donc aux élèves et aux enseignants la possibilité d’expérimenter une méthode originale et constructiviste dédiée au calcul mental, dans l’esprit des méthodes d’apprentissage nouvelles et adaptées à notre monde contemporain, type méthode de Singapour ou pédagogie Montessori, c’est-à-dire de modèles didactiques qui reposent sur le rôle privilégié du concret avant le passage à l’abstrait.

Aujourd’hui, une communauté naissante de bêta-testeurs incluant des partenaires du milieu éducatif, des élèves du primaire et du secondaire mais aussi quelques parents curieux et intéressés, envisage des améliorations. Ces requêtes et idées, souvent pertinentes, ouvrent pour la plupart des chantiers coûteux et donc des moyens financiers dont nous ne disposons pas encore. Parmi ces chantiers cruciaux et dont dépend la viabilité du projet, il a été retenu une mécanique de jeu plus développée afin de correspondre davantage aux attentes des élèves (trophées, épreuves, défis, graphisme plus dynamique…), ainsi que davantage de scénarios pédagogiques avec plus de thématiques, des comptes utilisateurs permettant un meilleur suivi statistique des performances individuelles, et un mode multi-joueurs indispensable dans l’univers du jeu où pratiquement tout se fait aujourd’hui ensemble, sur serveur, via les réseaux sociaux ou via des plates-formes indépendantes.

Le développement d’une communauté plus large permet de multiplier les retours, les échanges, les réflexions menées autour de la pratique, et constitue de ce fait une étape primordiale pour le développement du projet dans lequel s’inscrit HowMany.

Nous espérons vous avoir convaincus de nous rejoindre dans l’aventure et nous vous invitons à partager vos propres expériences !