L’histogramme sous une autre facette

L’histogramme est une notion souvent mal définie avec des graphiques quelquefois erronés, à commencer dans les manuels. Charlotte Derouet redonne ici du sens à cette représentation graphique et montre notamment son intérêt pour introduire la notion de fonction de densité de probabilité.

Charlotte Derouet

© APMEP Juin 2018

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

L’histogramme ou la représentation graphique mal aimée

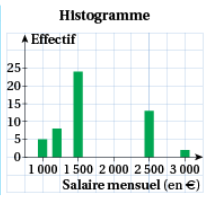
Bien que présente dans les programmes de mathématiques dès le début du cycle 4, la notion d’histogramme est pourtant mal connue des élèves tout au long de leur scolarité secondaire mais parfois aussi des enseignants. Il suffit d’ouvrir les manuels de collège et lycée pour rencontrer des « histogrammes » qui n’en sont pas, des définitions de la notion qui ne sont pas satisfaisantes… Une analyse de manuels de la classe de seconde [3] a détaillé les différentes erreurs que l’on peut trouver sur cette notion. Notamment, on peut trouver parfois des histogrammes qui ne sont rien d’autres que des diagrammes en bâtons (figure 1).

Pour le graphique de droite, l’erreur peut paraître subtile voire inexistante, mais que serait le graphique si les intervalles considérés n’étaient pas de même amplitude ? Certainement exactement le même avec simplement un changement au niveau de l’écriture des intervalles (mais pas dans la largeur des rectangles). Le tableur qui appelle « histogramme » le diagramme en bâtons¹ est certainement une des explications à la mauvaise appréciation de cette représentation graphique.

Figure 1 : Extraits du manuel Odyssée seconde² , p. 265 et p. 281.↩

L’analyse précise des manuels a permis de conclure que la notion d’histogramme est très mal maîtrisée par les auteurs de manuels et donc de formuler l’hypothèse qu’il pourrait en être de même pour les enseignants et leurs élèves.

Une étude [6] fait apparaître que les enseignants, au lycée comme au collège, ne consacrent que très peu de temps à l’histogramme (environ une heure par an) et que près de la moitié des enseignants interrogés estiment que « l’enseignement de l’histogramme ne contribue pas à la formation mathématique des élèves » (p. 131). Le manque de sens ainsi que le manque d’intérêt porté à cette représentation graphique expliquent ce constat.

Cependant, tout comme le précise Roditi [6] , je pense que l’histogramme peut être un appui important et pertinent pour introduire la notion de fonction de densité de probabilité et donc les lois à densité, notamment en terminale scientifique [2], [3]. En effet, le lien entre histogramme et courbe de densité est à mettre en correspondance avec le lien entre fréquence et probabilité qui est utilisé en classe dès le collège. Il s’agit implicitement de la loi faible des grands nombres, dont la formulation vulgarisée proposée (dans le cas fini) dans le document d’accompagnement du programme de 2001 de la classe de première S [5] est la suivante: « Si on choisit \(n\) éléments d’un ensemble fini \(E\) selon une loi de probabilité \(P\), indépendamment les uns des autres, alors la distribution des fréquences est proche de la loi de probabilité \(P\) lorsque \(n\) est grand ».

En effet, si par exemple on simule plusieurs échantillons de taille suffisamment grande de variables aléatoires suivant une loi uniforme sur \([0\,; 1]\), on peut voir que le haut des rectangles des histogrammes est « proche » de la courbe représentative d’une fonction constante sur \([0\,; 1]\).

Encore faut-il dans un premier temps bien définir ce qu’est un histogramme et lui donner du sens pour pouvoir s’en servir pour introduire une autre notion. Tout d’abord, il me semble indispensable, avant de définir un histogramme, de définir ce qu’est la densité de fréquence. Une analogie qui me semble adaptée pour les élèves et que je reprends de Bressoud & Kahané [1] est celle avec la densité de population. Voici leur exemple :

Ainsi, une représentation pertinente des populations de Monaco et du Japon doit rendre visible cette différence de densité.

Il en est de même quand l’on cherche à représenter des fréquences de classes (notamment si elles sont d’amplitudes différentes) : il n’est pas pertinent, par exemple, de représenter de la même façon une fréquence égale à \(0,05\) de la classe \([6\,; 11[\) et de la classe \([80\,; 110[\). Ces deux classes d’âge ont la même fréquence mais l’amplitude de la première classe est inférieure à celle de la seconde, on pressent que la densité de la première classe est supérieure à celle de la seconde. Par analogie avec la densité de population utilisée en géographie, on calculera le quotient de la fréquence d’une classe d’âge par l’amplitude de cette classe, et on parlera de densité de fréquence. Comme perçue, la densité de fréquence de la première tranche d’âge est plus grande que la densité de fréquence de la seconde tranche d’âge. La représentation graphique, qui n’est autre que l’histogramme, doit rendre visible ce phénomène.

Je propose donc les définitions suivantes :

• Dans le cas d’une variable quantitative continue, on définit la densité de fréquence \(d_i\) d’une classe de fréquence \(f_i\) et d’amplitude \(a_i\) par : \(d_i= \dfrac{f_i}{a_i}\) ;

• Un histogramme de fréquences est un diagramme composé de rectangles collés dont les aires sont proportionnelles aux fréquences et dont les bases sont déterminées par les intervalles des classes.

Nous trouvons donc que l’axe des ordonnées représente la densité de fréquence (à constante multiplicative près), et non la fréquence comme on peut le voir très souvent dans les manuels (cf. figure 1). Bien entendu, fréquence et densité sont égales (ou tout du moins proportionnelles) lorsque les amplitudes des classes sont égales, mais tout de même ! L’histogramme n’a pas vocation à avoir seulement des classes de même amplitude.

Maintenant que les choses sont (plus) claires, je vais présenter une proposition d’introduction de la notion de fonction de densité prenant appui sur la notion d’histogramme expérimentée dans plusieurs classes de terminale S (vous trouverez plus de détails sur cette expérimentation dans [2]).

Une introduction de la notion de fonction de densité prenant appui sur l’histogramme

Si l’on regarde les activités d’introduction des manuels de terminale S (édition 2012) du chapitre sur les lois à densité, cinq manuels proposent un passage par l’histogramme pour introduire la courbe de densité de probabilités³. Cependant, beaucoup d’erreurs mathématiques sont présentes, notamment à nouveau sur la notion d’histogramme. De plus, aucune réelle réflexion sur la fonction (appelée ensuite fonction de densité) n’est attendue des élèves (la courbe est déjà tracée). Le travail est très guidé et finalement les propriétés qui caractérisent une fonction de densité sont imposées aux élèves.

L’idée dans la proposition présentée ci-dessous est que les élèves construisent et donnent réellement du sens à la notion de fonction de densité et donc que les différentes propriétés de la fonction de densité émergent de la situation.

Je présenterai ici seulement le premier des deux problèmes d’introduction de la notion de fonction de densité conçus en collaboration avec une enseignante. Je donnerai aussi des éléments du déroulement effectif dans sa classe de terminale S d’un lycée parisien (en 2015).

Il est à prendre en considération qu’en amont de ces séances, les élèves ont fait un devoir maison  autour de la notion d’histogramme avec notamment un appui sur les définitions données ci-dessus, pour que cette notion soit réellement disponible pour eux. Ils ont aussi eu une première approche de la loi uniforme continue (sans qu’elle soit nommée ainsi) avec une partie « intuitive », une partie simulation pour aboutir à des histogrammes et la recherche d’une « courbe de tendance ». En revanche, aucun travail n’a été fait avant sur le calcul intégral. La séquence a en effet l’originalité d’articuler à la fois les lois à densité et le calcul intégral, mais je n’insisterai pas sur ce point ici.

Le problème de modélisation donné aux élèves est le suivant :

On peut retrouver cette situation (que j’appelle le problème de la rencontre) dans le document Ressources Probabilités et statistiques de la classe de terminale [4] mais sous forme d’exercice d’application. Ici, l’énoncé est beaucoup plus ouvert et a pour objectif d’introduire la notion de fonction de densité.

La séance a duré deux heures en classe. Dans un premier temps, les élèves ont une phase de recherche individuelle. Une première mise en commun permet alors d’engager des discussions dans la classe sur la vraisemblance ou non du problème, sur le caractère aléatoire de la situation, sur le caractère discret ou continu du temps… Des considérations qualitatives peuvent alors arriver, comme par exemple : le temps d’attente est entre \(0\) et \(1\) heure, il y a plus de chances que le premier arrivé attende \(5\) minutes que \(55\) minutes…

Progressivement, des variables aléatoires \(T_O\) et \(T_K\) représentant respectivement les heures d’arrivée d’Olivier et Karine sont introduites par les élèves et la variable aléatoire \(X\) représentant le temps d’attente est définie par \(X=|T_O-T_K|\). Ayant rencontré dans le devoir maison des simulations et ensuit une mise sous forme d’histogrammes, les élèves proposent assez naturellement (bien que cela puisse mettre du temps) de simuler des réalisations de la variable aléatoire \(X\) et ensuite de les représenter sous forme d’histogramme.

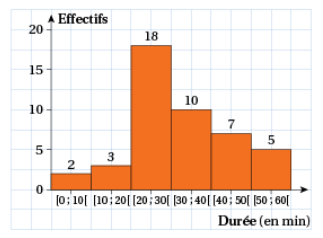
Le logiciel GeoGebra permet d’obtenir par exemple l’histogramme⁴ de la figure 2 ci-dessous.

Figure 2 : Histogramme d’un échantillon de taille 10 000, classes d’amplitude 5 minutes.

Les élèves cherchent ensuite une « courbe de tendance » en prenant en compte l’allure de l’histogramme, courbe qui semble être un segment. Cependant, il faut une réflexion collective pour faire émerger le besoin d’imposer des contraintes pour choisir ce segment, notamment que l’aire sous la courbe fasse \(1\) sur \([0\,; 1]\) et que \(f(1)=0\), ce qui permet d’arriver à l’expression de la fonction suivante : \[f(x)=-2x+2.\] À partir de cette expression, il est possible de déterminer toutes les probabilités que l’on veut.

Cette présentation succincte du problème et de son déroulement permet de montrer un problème qui prend appui sur l’histogramme pour introduire une notion importante en terminale S pour véritablement comprendre les lois à densité : la fonction de densité.

Je souhaite maintenant illustrer, à travers la synthèse faite en classe et des extraits de verbatim, les savoirs qui ressortent de cette situation et notamment les justifications données par les élèves sur les propriétés de la fonction de densité mettant en évidence l’importance des connaissances sur les histogrammes.

Lors de la séance suivant la recherche autour du problème de la rencontre, l’enseignante propose un temps d’institutionnalisation. La synthèse écrite au tableau, construite au fur et à mesure avec les élèves, est la suivante⁵ :

L’enseignante introduit elle-même le vocabulaire « fonction de densité de probabilité », cependant elle demande ensuite aux élèves s’ils peuvent justifier ce choix de vocabulaire.

Voici la réponse d’un élève :

\(\mathrm{E}_1\) : c’est parce que sur l’axe des ordonnées, c’est la densité.

Pour justifier la positivité de la fonction de densité puis le fait que l’aire sous la courbe est égale à \(1\), on retrouve à nouveau une justification donnée par deux autres élèves prenant appui sur l’histogramme :

\(\mathrm{E}_2\) : parce qu’en fait c’est par rapport à l’histogramme donc on peut pas avoir de rectangles en-dessous.

\(\mathrm{E}_3\) : parce que ça correspond à la fréquence. L’aire correspond… […] L’aire correspond à la somme de toutes les probabilités… […] La somme des fréquences.

\(\mathrm{P}\) : et donc on sait que ça fait…

\(\mathrm{E}_3\) : un.

La construction de la nouvelle notion fonction de densité est ici possible grâce à la disponibilité des connaissances sur l’histogramme. Notamment, le fait que l’axe des ordonnées de l’histogramme soit véritablement défini et ait un sens pour les élèves permet de légitimer le vocabulaire « fonction de densité de probabilité », ce qui n’est jamais fait dans les manuels.

Conclusion

J’espère avoir montré l’intérêt et l’utilité de l’histogramme, si ce n’est pour lui-même comme moyen pour représenter des données statistiques (continues ou tout du moins regroupées), au moins pour l’étude des lois à densité et notamment pour l’introduction de la fonction de densité. Ce chapitre qui est très conséquent en terminale (pas seulement en terminale S) peut dépasser la simple mémorisation de formule si un véritable travail d’introduction de la notion de fonction de densité est fait. Il semble donc important de former les enseignants sur l’histogramme pour que leur point de vue à son sujet change et qu’ils en perçoivent les enjeux notamment en probabilités.

Références

1. E. Bressoud et J.-C. Kahané. Statistique descriptive. 2e édition. Pearson France, 2010. ↩

2. C. Derouet. « La fonction de densité au carrefour entre probabilités et analyse. Étude de la conception et de la mise en oeuvre de tâches d’introduction articulant lois à densité et calcul intégral ». Thèse de doctorat. Université Paris Diderot, 2016. ↩

3. C. Derouet et B. Parzysz. « How can histograms be useful for introducing continuous probability distributions? » In : ZDM – Mathematics Education 48.6 (2016), p. 757-774. ↩

4. Ministère de l’Éducation nationale de la Jeunesse et de la Vie associative (MENJVA) et DGESCO. Ressources pour la classe terminale générale et technologique : probabilités et statistique. Paris, 2012. ↩

5. Ministère de l’Éducation nationale et Direction de l’Enseignement Scolaire. Mathématiques : classe de première des séries générales. Paris : Centre national de documentation pédagogique, 2001. ↩

6. É. Roditi. « L’histogramme : à la recherche du savoir à enseigner ». In : Spirale. Revue de recherches en éducation 43 (2009), p. 129-138. ↩

Charlotte Derouet est maître de conférences en didactique des mathématiques à l’ÉSPÉ de l’académie de Strasbourg et membre du LISÉC (Laboratoire Interuniversitaire des Sciences de l’Éducation et de la Communication).